鋰電池組線性二次型調節器對散熱性能的優化控制

安治國,黎代林

(重慶交通大學 機電與車輛工程學院, 重慶 400074)

0 引言

由于傳統能源日益減少、環境污染日趨嚴重,新能源汽車的發展有效促進了汽車的節能減排,有助于降低環境污染和碳排放。在新能源汽車中,鋰電池作為儲能單元的電動汽車(EV)正在快速發展。與其他類型的電池相比,鋰電池因其功率密度高、壽命長、自放電率低、成本低等優點,得到了廣泛的應用[1-3]。隨著EV對快充需求的不斷提高,電池在快充時,由于大功率、大電流的影響使產熱量迅速升高,如果電池溫度控制不當,會導致電池性能下降,壽命縮短,甚至造成燃燒或爆炸等安全事故[4-5]。因此,鋰電池在快充條件下的實時控制已成為EV發展急待解決的核心問題之一。

許多學者對鋰電池充放電過程的電池生熱做了深入研究,一般認為鋰電池的最佳工作溫度為20～40 ℃[6-7]。Li等[8]研究了由 14 節柱狀鋰電池組成的電池組的內阻和電化學反應所產生的熱量。結果表明,在5C放電條件下的電池組溫度迅速升高,引發熱失控現象。在冷卻劑流速較低時,難以將電池組產生的熱量散去。通過提高冷卻劑流速才能更好地控制電池組溫度。Mao等[9]強調溫度每升高1℃,電池的使用壽命減少2個月。因此,電池熱管理系統(BTMS)的設計對鋰電池的性能具有重要影響[10]。目前,EV中應用最多的冷卻方式是風冷和液冷,風冷熱管理系統的熱交換效率低于液冷熱管理系統[11],不能滿足快充快放條件下的電池散熱需求。液冷熱管理通過冷卻液間接與電池體接觸,可以快速帶走熱量,從而保證電池的可靠使用,因此,液冷BTMS可以滿足快充快放需求。

液冷BTMS的研究主要集中在冷卻板的結構和控制器設計2個方面。在冷卻板結構設計方面,許多學者已經提出多種提高散熱性能的方案[12-14]。相對于冷卻板的結構設計,液冷BTMS控制器的設計仍處于起步階段。在液冷控制中,林曉偉等[15]通過搭建熱電耦合模型估算鋰電池的產熱量,利用PID 算法對鋰電池包的溫度進行控制。結果表明,電池包的溫度可以控制在合理值范圍,但PID控制器控制的電池溫度系統冷卻速度較慢,控制精度不理想。Tang等[16]提出了用粒子群算法優化向量回歸的控制方法(PSO-SVR)來計算BTMS的冷卻能力和系統性能系數。結果表明,在PSO-SVR控制的BTMS下的制冷量和性能系數提高了2.1%和2.8%,系統冷卻能力提高了86.8%。但SVR模型過于復雜,不易于實際應用。馬彥等[17]提出了一種空間迭代的方法來逼近最優值的規劃策略(IDP),用來研究BTMS的冷卻性能。結果表明,在IDP控制的BTMS的冷卻速度得以提高,冷卻能耗降低。但IDP算法需要比較BTMS的控制量與狀態量,需要大量內存空間來存儲控制量和狀態量,計算時間過長,無法準確及實時控制。陳思琦等[18]提出了一種基于神經網絡的回歸模型的方法來控制BTMS的最高溫度、溫差以及功耗。結果表明,最高溫度可以控制在33.35 ℃,溫差可以控制到0.8 ℃。但神經網絡模型需要設計多組不同充電倍率和多組不同冷卻液流量,最終從方案組中得到最優解的過程,方案組的設計需要龐大的數據集。因此,神經網絡回歸模型需要強大的計算能力,控制要求過高。綜上所述,在液冷BTMS控制器的設計方面雖然取得了一些成績,但研究還很不充分,成果主要集中在低倍率充電的溫度控制上,對于在快充及實際工況下鋰電池液冷BTMS的控制方面的研究仍存在不足。

為解決上述問題,針對鋰電池液冷BTMS在快充和3C-NEDC的工況,提出了一種線性二次型調節器(LQR),通過仿真比較研究LQR控制器對液冷BTMS的最高溫度、溫差和能耗的控制效果。

1 模型與方法

1.1 電池模型

1.1.1電池組幾何模型

電池組結構如圖1所示,系統包含8個圓柱形鋰電池,電池組兩側冷卻管并行排列與電池組緊密貼合,表1所示為電池主要參數。電池模組的產熱量為Qt,液冷傳熱量為Ql。冷卻液入口和出口設置為2種不同情況:方式1,即2個流道的冷卻液出入口反向布置;方式2,即2個流道的冷卻液出入口同向布置。

圖1 電池組結構示意圖

表1 電池主要參數

1.1.2電池的產熱模型

基于水冷方式的電池組散熱性能研究需要對鋰電池內部產熱原理進行分析。鋰電池的產熱由4個部分構成,Qr、Qj、Qk、Qw分別為內阻熱、反應熱、極化熱、副反應熱。電池總產熱記為Qt,可由式 (1)表示:

Qt=Qr+Qj+Qk+Qw

(1)

假設電池內部的電流密度一致,Qk是由于電池工作時產生的極化內阻,在電流作用時產生的熱量。Qw是鋰電池自放電時產生的熱量,2種產熱的速率較慢,對電池溫度的影響較小,在本文中可以忽略。因此,式(1)可以簡化為:

Qt=Qr+Qj

(2)

電池在充放電過程的產熱主要集中在電池內部、正負極極耳,電池的產熱與充放電的電流、電量以及環境溫度等參數有關。由D.Bernardi等[19]提出的電池產熱率模型如下:

(3)

式中:I為電池工作的工況電流;Eoc為開路電壓;U為電池工作的端電壓;TBat為電池溫度; dEoc/dTBat為溫度系數。從式(3)可知,電池熱模型與電池的工況電流、開路電壓、溫度系數有關,具有非線性。

1.1.3電池的傳熱模型

得到電池的產熱模型后,根據傅里葉熱傳導定律可知,電池與外界介質進行熱交換的方式有熱傳導φ1、熱對流φ2以及熱輻射φ3,電池的總散熱量方程Qc為

(4)

式中:γ為電池與水的換熱系數;S為水流道的橫截面積;αT/αX為電池產熱速率;ΔT1為水與電池的溫差;ΔT2為熱力學溫度。由式(3)和式(4)可得,電池在經過水冷散熱后的電池熱模型記為Ql:

Ql=Qt-Qc

(5)

式中:Ql是電池在單位時間內產生的熱量,可以由下式表示:

(6)

(7)

水冷對電池進行冷卻,由牛頓冷卻公式可得:

Qc=γS(TBat-TIn)

(8)

式中:TBat為電池的溫度;TIn為水的溫度。由于電池的溫度變化與換熱系數有關,而換熱系數的大小與水流速相關,可以將γ表示:

γ=6 325vin

(9)

1.1.4等效電路模型

鋰電池在充放電過程中,產熱、散熱模型與電池的電特性有較強的耦合關系。鋰電池的等效電路模型可以由二階RC等效電路模型、三階RC等效電路模型甚至更高的等效電路模型構成,而高階RC等效電路模型的復雜性高,從文獻[20]研究分析,二階RC等效電路模型有高度精確性和低復雜性的特點,更適合數學模型研究。因此,采用二階RC模型表示電池的電特性模型。

如圖2所示,Eoc為電池的開路電壓,U為端電壓,Cs和Cl為極化電容,Rs與Rl為極化電阻,R0為等效內阻。

圖2 鋰電池二階等效電路模型

由圖2可得等效電路方程式:

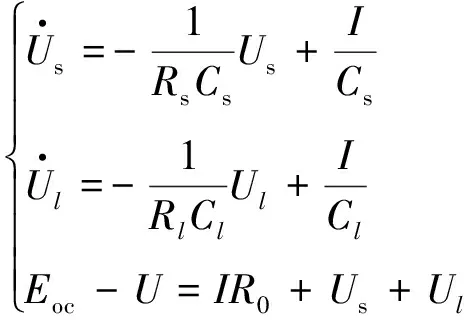
(10)

1.2 LQR控制算法

1.2.1電池的電熱耦合模型狀態空間方程

采用線性二次最優控制(LQR)方法,可以使BTMS用最低的功耗和以最快的響應速度對電池溫度進行冷卻。LQR控制器通過不同電池的極化電壓、電流、水流速加權得到最優控制量,是一種全狀態反饋控制器,用BTMS未來時段的工況電流、電壓和水流速作為系統的輸入。由式(7)、(8)、(9)、(10)整理可得:

由于LQR控制器的被控對象是線性定常系統,而本文的電池產熱-散熱模型是強非線性系統,需要進行模型線性化,由于工況電流的變化是時變的,需要設置多個平衡點對局部非線性模型線性化累加為全局模型線性化。對式(11)進行一階泰勒公式展開,可以得到電池的電-熱耦合模型的狀態空間方程:

(12)

1.2.2電池的電熱耦合模型目標函數

圖3為LQR控制器的工作流程框圖。控制器設計的重點在于A、B、C矩陣的確定以及狀態反饋矩陣K的設計。由狀態量ΔX與輸入量Δu通過狀態反饋矩陣K得到電池在流速控制后的溫度y。狀態量是電池的電壓、溫度,輸入量是水流速。

圖3 LQR控制器的工作流程

根據控制流程,由式(12)可以得到如下狀態方程

(13)

式中,Δu為可以表示為:

Δu=-K(Us+Ul+TBat)

(14)

式中,K的狀態反饋矩陣求解表示為:

K=R-1BTP

(15)

式中,P為黎卡提代數方程求解所得:

PA+ATP+Q-PBR-1BTP=0

(16)

BTMS的目標函數設計如下:

(17)

式中:β為不同工況的總時長;e為電池目標溫度與實際溫度的偏差;Q為狀態量的權重;R為輸入量的權重。

目標函數的設計可分為2種情況:① 對目標函數的溫度偏差e進行控制。② 對目標函數的流速變化進行控制。為了實現電池溫度實時控制,流速的邊界條件為0.5 m/s≥Vin≥0,R的取值為0.1,Q矩陣由式(18)表示。

(18)

為了使LQR控制器在全局具有高度可靠性,需要設置多個平衡點使電池在不同工況作用下產熱模型線性化。因此,在不同電流下,設置了多個狀態反饋矩陣K,如表2所示。

表2 反饋增益矩陣

1.3 電池熱管理系統搭建

1.3.1電池熱管理方案

圖4為電池組熱管理系統控制流程。根據不同的工況的電流得到該工況的電池溫度,通過監測首個電池溫度TBat1與末尾電池溫度TBat8(如圖1),取2個電池溫度的最大值作為最高溫度TBat,TBat>36 ℃時啟動BTMS。分別采用恒流速控制、PID控制以及LQR控制,由3個控制器模型得到流速控制曲線,通過水泵輸出,最后判斷工況是否結束,工況結束則停止冷卻,否則繼續開啟水泵輸出。

圖4 電池組熱管理系統控制流程流程

1.3.2熱管理系統建模

為了驗證模型的可靠性,對Amesim軟件搭建的電池電-熱耦合模型、Simulink搭建的BTMS數學模型進行比較。搭建的電池組電-熱耦合模型如圖5所示。圖5(a)為 Amesim平臺搭建的系統模型,系統由8個單體電池組成,水流道按照圖1設置。系統主要由冷卻管道、電池熱模型、電池電模型、工況電流輸入模塊和DC-DC轉換模塊構成。圖5(b)為Matlab-Simulink軟件搭建的電池組散熱模型,包括電池的產熱模型、電池的散熱模型以及LQR控制器、PID控制器、恒流速控制器。其中,恒流速控制器流速v為0.06 m/s,PID控制器需要經過多次調節,得出適合的比例、積分及微分參數值,分別為0.01、0.001和1。

圖5 電池組電-熱耦合模型示意圖

為了研究LQR控制器的控制下電池熱管理系統散熱性能,設定環境溫度為25 ℃,冷卻液為初始溫度20 ℃的水。在3C-NEDC(3C充電-NEDC放電)工況下對LQR控制器、PID控制器、恒流速控制器的響應時間和穩定性、電池組溫差及系統能耗3個方面進行對比研究。

1.3.3實驗裝置及步驟

電池組充放電實驗原理和實驗裝置如圖6所示。其中,內阻測試儀用于測量電池的內阻,用于仿真分析。溫度測試采用多路溫度記錄儀實時采集電池組不同位置的電池溫度。充電設備以3C充電倍率對電池組充電。放電設備以不同工況電流對電池組放電。恒溫箱用于調節實驗的環境溫度。水冷系統主要包括水箱、水泵、分流器、流量計和電池散熱器,實現電池組的熱管理。控制器的主要功能是控制水泵的輸出功率,并將數據上傳到計算機。萬用表用于測量電池的端電壓,判斷電池的荷電狀態。

圖6 電池組充放電實驗原理和實驗裝置圖

充放電實驗主要步驟如下:

1) 將電池組放入恒溫箱內,將實驗環境溫度設定為25 ℃。

2) 以1C的放電倍率對電池組進行放電,直到電池電量為5%。

3) 以3C充電倍率對電池組進行充電,并按照NEDC和US06工況設置好放電設備的放電電流,在充電結束后進行相應工況的放電操作。

4) 充放電過程中,利用溫度記錄儀實時采集電池組的溫度,控制器控制水泵的輸出功率,并將數據上傳到計算機。

1.3.4模型可靠性驗證

為了驗證電池熱管理模型的可靠性,分別對比了在NEDC和US06兩種工況下Simulink模型、Amesim模型和充放電實驗的溫度誤差,如圖7所示。

圖7 不同工況電池溫度變化和模型誤差

圖7(a)和(b)分別為NEDC和US06工況的電流變化曲線,圖7(c)和(d)分別表示模型在自然對流條件下,在NEDC工況和US06工況時的電池溫度和溫度誤差曲線。從圖7(c)可以看出,在NEDC工況下,Simulink模型、Amesim模型和充放電實驗得到的電池組的最高溫度分別為33.92、34.45和34.84 ℃。NEDC工況下,仿真和物理實驗的最大溫度誤差為0.91 ℃。從圖7(d)可以看出,在US06工況下,Simulink模型、Amesim模型和充放電實驗得到的電池組最高溫度分別為26.9、26.95和27.1 ℃,仿真和物理實驗的最大溫度誤差為0.21 ℃。由以上對比分析可知,2種工況下仿真和物理實驗的最大溫度誤差值均小于1 ℃,仿真模型的可靠性較好。

2 結果與討論

2.1 控制器對BTMS的響應時間和穩定性的影響

在3C-NEDC的工況下,對方式1所示電池組進行充放電仿真實驗,得到3C-NEDC工況電流與電池溫度曲線,如圖8所示。由圖8(a)可以看出,電池3C充電電流為8.1 A,1 200 s時充電過程結束,此后按照NEDC工況開始放電,充放電總時長為2 632 s。圖8(b)所示為自然對流條件以及在3個不同控制器作用下的電池溫度曲線。從圖8(b)中可以看出,自然對流條件下,電池的最高溫度為54.6 ℃,遠高于電池的合理工作溫度上限40 ℃,不能滿足電池組散熱要求。與自然對流相比,3種不同控制方式的電池溫度曲線明顯得到改善,放電過程中,電池組溫度均可控制在合理工作溫度范圍之內。

在圖8(b)中,將目標控制溫度Td設為25 ℃時,系統誤差帶δ設為±2%。根據時域分析,可以得出LQR控制器的響應時間T1為1 198 s,PID控制器的響應時間為T2為1 244 s,恒流速控制器的響應時間T3為1 301 s。對比3種控制器效果,LQR的冷卻響應速度最快,PID次之,恒流速控制最慢。

從圖8(b)可以看出,3種控制器的穩定性差異明顯。在時間段為2 235～2 539 s時,LQR控制器的控制穩定性較好,PID控制與恒流速控制的電池溫度曲線超過誤差帶δ,超出溫度的最大值分別為25.8和26.2 ℃。原因是,PID是根據電池溫度和目標溫度的偏差大小進行控制的,工況電流的變化劇烈,電池自身的產熱也會加劇,而PID控制器的控制輸出具有時滯性,從而使電池溫度超出誤差帶范圍。恒流速控制方式是恒定流速輸出控制,對電池的產熱并不具備實時調節能力。而LQR控制是根據工況電流、電池開路電壓以及內阻,通過反饋增益矩陣計算輸出流速的,可以對電池在工況作用下的產熱計算合理的流速。

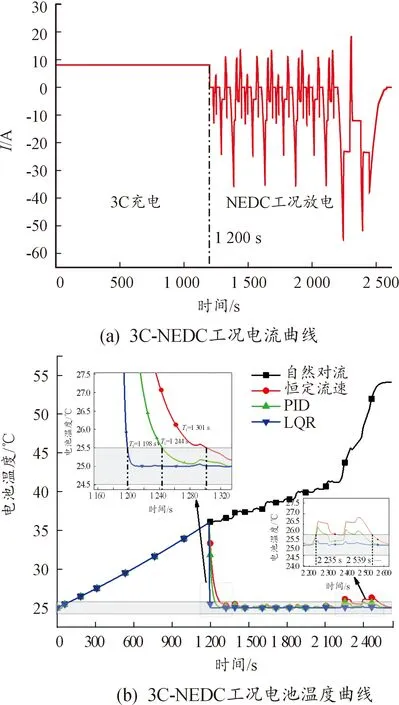
圖8 3C-NEDC工況電流與電池組散熱曲線

2.2 控制器對BTMS溫差的影響

為了研究電池不同方式在3C-NEDC工況下的溫差情況,對方式1和方式2所示電池組進行充放電仿真實驗,通過監測TBat1與TBat8的最高溫度,得到不同控制器對電池組溫差的影響曲線,如圖9所示。圖9(a)和(b)分別為方式1和方式2電池組在恒流速控制器控制下的電池溫度和電池溫差曲線。可以看出,方式1和方式2電池的最大溫差E分別為2.9 ℃和1.28 ℃。與方式1相比,方式2電池組溫差減少了1.62 ℃。

圖9(c)和(d)分別為方式1和方式2電池組在PID控制器控制下的電池溫度和電池溫差曲線。可以看出,方式1和方式2電池的最大溫差E分別為2.56 ℃和1.53 ℃。與方式1相比,方式2電池組溫差減少了1.03 ℃。

圖9(e)和(f)分別為方式1和方式2電池組在LQR控制器控制下的電池溫度和電池溫差曲線。可以看出,方式1和方式2電池的最大溫差E分別為3.57 ℃和1.1 ℃。與方式1相比,方式2電池組溫差減少了2.47 ℃。

對比3種控制器對BTMS的最大溫差控制效果,LQR在方式2電池組控制的溫差的控制效果最好。這是由于LQR控制器在冷卻開始的流速較大,從而使冷卻液可以快速地帶走電池熱量,進而減小TBat1和TBat8的溫差,而PID控制器由于系統響應時間長,啟動后不能及時帶走大量的熱量,使BTMS的最大溫差變大。對于恒定流速控制,因不具備流速調節能力,使啟動后帶走的熱量最少,BTMS的溫差最大。

圖9 不同控制器對電池組溫差的影響

2.3 控制器對冷卻能耗的影響

為了研究電池不同方式在3C-NEDC工況下的冷卻能耗情況,對電池組進行充放電仿真實驗,通過監測水泵的能耗得到不同控制器對BTMS冷卻能耗曲線,如圖10所示。由圖10可以看出,在充電過程中,時間1 190 s時電池溫度達到控制器啟動溫度36 ℃,水泵開始工作。在1 190 s～1 790 s,LQR控制器的冷卻平均能耗最大,其次是PID,最小為恒定流速。在時間為1 790 s后,LQR控制器作用下水泵平均能耗開始減小,PID控制器開始增加,恒定流速控制器不變。從控制器啟動至放電結束,LQR控制器作用的平均冷卻能耗為6.05 W,PID控制器平均冷卻能耗為6.18 W,恒定流速控制器平均冷卻能耗為6.1 W。LQR控制器作用比PID和恒定流速控制器平均冷卻能耗分別減少了2.1%和0.8%。這是因為,LQR控制器的設計以減少冷卻能耗為目標,對流速的輸出和能耗起到最優控制。

圖10 不同控制器冷卻能耗

3 結論

1) 搭建的Simulink數學模型、Amesim電池的電-熱耦合模型以及實驗模型具有較高的可靠性,模型電池溫度誤差小于1 ℃。

2) 在3C-NEDC工況下,LQR控制器作用的BTMS響應時間比PID及恒定流速控制器更短,并且LQR控制器控制下電池溫度沒有超過系統誤差帶,系統具有較高的控制穩定性。

3) 對比3種控制器對BTMS的最大溫差控制效果,LQR控制器在電池組液冷管道反向布置時,電池組溫差最小,控制效果最好。

4) 與PID及恒定流速控制器相比,LQR控制器的冷卻能耗比PID控制器減少2.1%,比恒定流速控制減少0.8%。