基于改進型偏最小二乘法的諧波源識別

張建明 趙巧玲 賈遠溫

（1．蘭州倚能電力設計咨詢有限公司，甘肅 蘭州 730050；2．蘭州資源環境職業技術大學，甘肅 蘭州 730030）

0 引言

由于各種非線性負荷大量應用到實際生產中，因此一次諧波也日益凸顯。諧波不僅會導致用電設備發生故障，而且還會影響整個電網的運行情況。

諧波源識別主要有2 種方法：1） 基于諧波狀態估計法[1]。它可以通過計算系統各節點諧波電壓及支路諧波電流來判斷諧波源的位置。2） 將供電系統等效成系統U（Utility）和用戶C（Customer），由相應等效電路模型確定諧波源的位置[2]。為了準確識別系統中各個諧波源，該文利用改進型偏最小二乘法[3]進行研究，用估計值代替實際測量值，同時結合阻抗法，通過諧波電流的大小來判斷主要諧波源，從而識別諧波源的位置。

1 改進型偏最小二乘法原理

由等效電路模型確定諧波源的方法主要包括功功率法[4]、無功功率法[5-8]以及線性回歸法[9-11]等。當采用傳統的偏最小二乘法時，有可能出現遺漏一些成分的情況，這些成分可以很好地反應響應變量，從而使回歸結果存在較大誤差。因此，需要對其進行改進，即采用正交投影法消除解釋矩陣中與響應變量沒有統計學意義的信息。經過改進后，解釋矩陣中的信息就全部與響應變量有統計學意義了，可以達到偏最小二乘回歸法的要求，再采用該方法進行相應變換。實施方法如下 ：1） 解出矩陣的全部特征值，解得q-1 個正交特征向量a1、a2、...、aq-1，這些特征向量與全部特征值0 有統計學意義。2） 得到矩陣BTXTXB的q-1 個特征值λ1、λ2、...、λq-1，同時得到各個特征值所對應的標準特征向量α1、α2、...、αq-1，再篩選相對較大的m個α1、α2、...、αm，使它們的和在所有特征值之和中占較大的比重。3） 設C=XBA，矩陣A=（α1、α2、...、αm），那么C就是要采用正交投影法去除的成分。4） 在C上對解釋矩陣X進行投影處理，就可以得到公式（1），X0可以采用偏最小二乘法對因變量矩陣Y進行回歸計算。5） 采用偏最小二乘法使Y對X0進行回歸計算，得到Y1=X0、α=Xβ，那么β便是采用改進型偏最小二乘法對X進行回歸所得的系數。

式中：B為回歸系數的估計量；X為自變量矩陣；D為回歸系數；Pc為回歸系數矩陣；Ip為解釋矩陣。

2 諧波源識別的基本原理

如果要識別系統中的諧波源，就要比較在公共耦合點處流向系統側諧波電流與流向負荷側諧波電流的大小。當從系統側流出的諧波電流大于從負荷側流出的諧波電流時，說明系統側是主諧波源，反之就說明負荷側是主諧波源。該文采用改進型偏最小二乘法對諧波阻抗進行估算，用估算得到的諧波阻抗判斷諧波源電壓或電流的大小，從而得到主要的諧波源。系統等效電路如圖1 所示。

圖1 系統等效電路圖

由圖1 可知，從負荷側流出的h次諧波電流Iuh如公式（2）所示。

從供電端流出的h次諧波電流Idh如公式（3）所示。

比較Idh和Iuh的大小可以確定主諧波源。因為無法直接測量阻抗，所以該文采用改進型偏最小二乘法估算諧波阻抗。

改進型偏最小二乘回歸法的主要內容如下：經測量得到公共耦合點的諧波電壓信號、諧波電流信號，再通過測量值評估諧波阻抗和諧波電壓的大小。

諧波源檢測模型如圖2 所示，根據模型電路圖就可以得出相應的方程，如公式（4）所示。

圖2 諧波源檢測模型

將公式（4）的實部和虛部展開就有公式（5）、公式（6）。

式中：Ushx為系統側的h次諧波電壓源的實部；Ushy為系統側的h次諧波電壓源的虛部；Upcchx為公共耦合點的h次諧波電壓的實部；Upcchy為公共耦合點的h次諧波電壓的虛部；Ipcchx為公共耦合點的h次次諧波電流的實部；Ipcchy為公共耦合點的h次次諧波電流的虛部；Zshx為系統側的h次諧波阻抗的實部；Zshy為系統側的h次諧波阻抗的虛部。

利用改進型偏最小二乘法對公式（5）、公式（6）進行回歸計算就可以得到回歸系數Ushx、Ushy、Zshx和Zshy，再根據回歸系數求得系統諧波阻抗的平均值，如公式（7）所示。

式中：n為分段數；Zshxi為第i段系統側h次諧波阻抗的實部；Zshyi為第i段諧波阻抗的虛部。

系統背景諧波電壓平均值如公式（8）所示。

式中：Ushxi為第i段系統側h次諧波電壓源的實部；Ushyi為第i段系統側h次諧波電壓源的虛部。

同理，將用戶側等效為戴維南等值電路，如圖3 所示。

圖3 系統戴維南等值電路

用戶側諧波阻抗平均值如公式（9）所示。

式中：Zchxi為第i段用戶側h次諧波阻抗的實部；Zchyi為第i段用戶側h次諧波阻抗的虛部。

用戶側諧波電壓平均值如公式（10）所示。

式中：Uchxi為第i段用戶側h次諧波電壓源的實部；Uchyi為第i段用戶側h次諧波電壓源的虛部。

將公式（7）～公式（10）的值代入公式（1）、公式（2），然后比較Idh和Iuh的大小，就可以判別諧波源的位置。

3 試驗分析

該文利用電力系統模塊集進行仿真試驗。假設在系統中存在1 個隨機擾動的諧波源，建立試驗仿真所需要的電路模型（如圖4 所示），由測量可以得到公共耦合點的諧波電壓和公共耦合點的電流，然后利用改進型偏最小二乘回歸對測量出的諧波電壓和電流進行分析，最終得到與原有設置值相近的估算值。

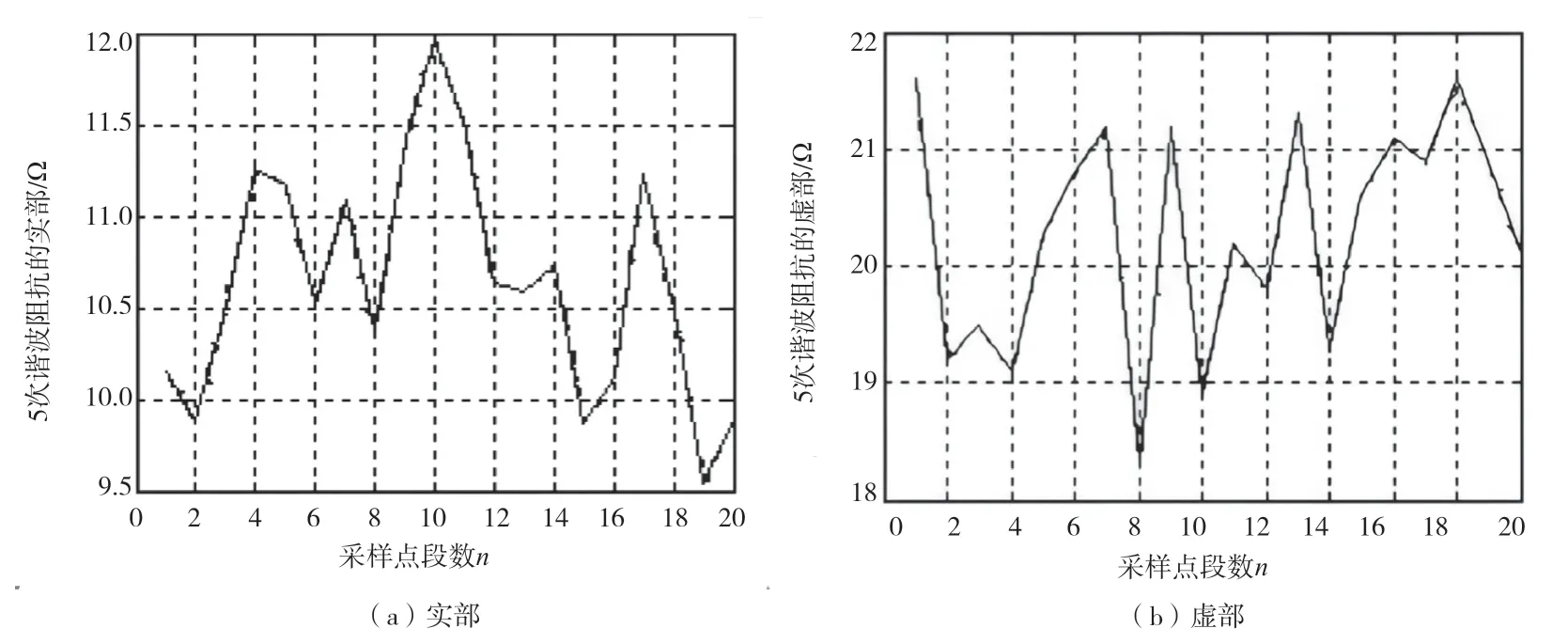
圖4 系統側的5 次諧波阻抗的實部和虛部

假設整個系統僅有5 次諧波，調整系統側的諧波電壓幅值，同時也調整用戶側的諧波源幅值，但是不能改變阻抗參數。系統側對應的等值5 次諧波電壓源Us為（5053°） V，用戶側對應的等值5 次諧波電壓源Uc的平均值為（90+j780） V，系統側對應的5 次諧波阻抗Zs平均值為（10+j20） Ω，用戶側對應的5 次諧波阻抗Zs的平均值為（50+j60） Ω。

在仿真的過程中，依次提取公共耦合點的5 次諧波電壓和諧波電流，采樣點數n為1 000 個（單位時間），總共分為20 段，每段有50 個點，然后對每段進行處理，即由改進型偏最小二乘回歸法得到電源系統側以及負荷用戶側的諧波阻抗，同時還需要計算諧波電壓源對應的實部和虛部，將計算出的每段諧波阻抗的平均值作為該段的諧波阻抗，也可以看作是諧波電壓源的實部和虛部（結果如圖4～ 圖 7 所示）。

圖5 系統側的5 次諧波電壓源的實部和虛部

圖6 用戶側的5 次諧波阻抗的實部和虛部

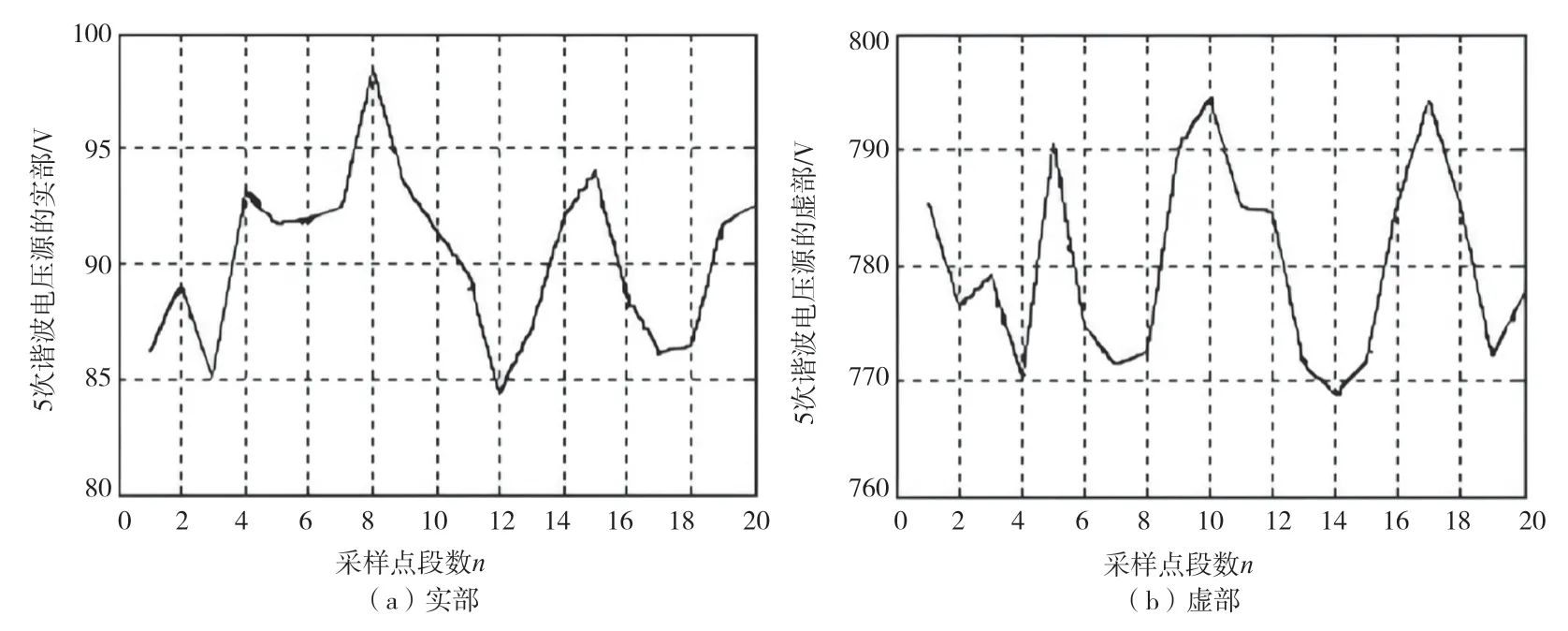
圖7 用戶側的5 次諧波電壓源的實部和虛部

運用改進型偏最小二乘回歸法可以得到系統側存在的5 次諧波阻抗Zs5的平均值，如公式（11）所示。

側存在的諧波電壓源Uc5的平均值，如公式（12）所示。

采用進型偏最小二乘回歸法可以得到用戶側存在的5次諧波阻抗Zc5的平均值，如公式（13）所示。

由各個段估計獲得的5 次諧波阻抗就可以得到用戶側諧波電壓源Uc5的平均值，如公式（14）所示。

用戶側5 次諧波電流Ic5的平均值如公式（15）所示。

式中：Upcc5和Ipcc5分別為公共耦合點的5 次諧波電壓以及5 次諧波電流。

將計算所得的數據代入公式（1）、公式（2）就可以得到從負荷側流出的5 次諧波電流、從供電端流出的5 次諧波電流，分別如公式（16）、公式（17）所示。

因為|Iu5|＞|Id5|，所以用戶側為主要諧波源。采用改進型偏最小二乘回歸法進行仿真試驗，主要針對系統的3 次諧波以及系統中其他各次諧波進行仿真計算，具體結果見表1。

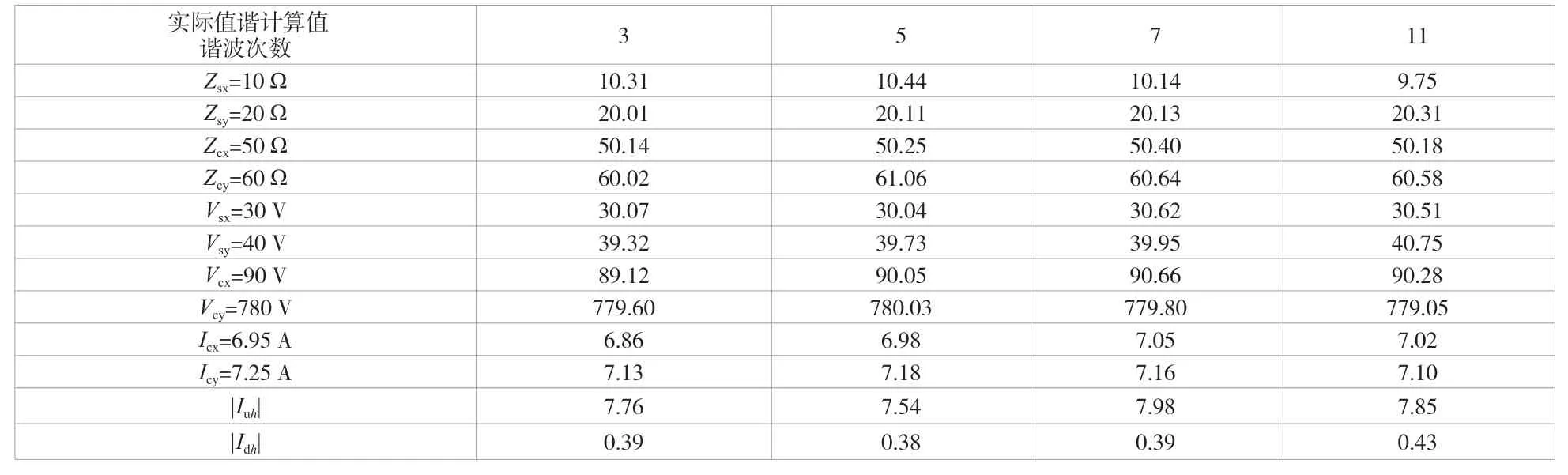
表1 各次諧波仿真計算表

由仿真結果可知，在諧波次數不同的情況下，當實際準確值與采用改進型偏最小二乘回歸法計算得出的估計值較相近且|Iuh|＞＞|Idh|時，用戶側為主要的諧波源，該結果與最初設想的結果相同。

4 結語

該文將改進型偏最小二乘法應用于系統諧波源識別，利用正交投影法消除解釋矩陣中與響應沒有統計學意義的信息，解決了偏最小二乘法會遺漏與響應有關成分的問題，提高了估算精度。首先，利用改進型偏最小二乘法與阻抗法識別主要諧波源，最初采用改進型的偏最小二乘法進行回歸計算，通過計算得出系統的諧波阻抗估計值。其次，與阻抗法相結合，得出諧波電流流出的大小，流出較多的一側為主要的諧波源。最后，將通過試驗仿真得到的數值與原有的設定值進行比較，從而驗證了該文提出的方法能夠快速、高效地識別諧波源。