自適應約束評估的代理模型輔助演化算法

魏鳳鳳，陳偉能+

1.華南理工大學 計算機科學與工程學院，廣州510006

2.華南理工大學 大數據與智能機器人教育部重點實驗室，廣州510006

演化算法（evolutionary algorithms，EAs）是求解復雜優化問題的常用方法，在求解傳統約束優化問題中有很好的效果[1-3]。然而在很多工程問題中，目標和約束的計算沒有明確的公式表達，需要仿真軟件模擬，甚至真實實驗才能獲得結果，這樣一次復雜目標和約束值的計算過程需要花費幾個小時甚至幾天，例如，一次20～50 維的毫米集成電路的仿真需要花費20～30 min[4]，這類問題被稱為昂貴優化問題。

傳統EAs 往往需要進行上萬甚至幾十萬次適應值評估才能得到滿意解，在求解昂貴優化問題中的時間代價是難以接受的。因此學者們提出基于代理模型輔助的演化方法（surrogate-assisted evolutionary algorithms,SAEAs）[5-6]，使用較少的歷史數據建立模型，用模型預測結果替代演化過程中真實適應值評估，從而降低時間成本，獲得滿意的優化結果。

當前SAEAs在求解昂貴無約束優化問題中已有較好發展[7-10]，但在處理昂貴約束優化問題方面仍有待研究。Sasena 等人比較了在高斯過程回歸模型的輔助下，現有的不同樣本選擇準則的性能差異[11]；Yannou 等人利用表面響應模型來擬合約束，并在約束編程環境中調研模型保真度和由此產生的約束可處理性之間的關系[12]；Singh 等人將代理模型嵌入到模擬退火算法來求解多目標昂貴約束優化問題[13]；Regis等人提出一種解決昂貴約束優化問題的徑向基函數輔助進化編程算法[14]；Singh 等人提出一種利用不可行解進行驅動的進化算法來求解軟約束和硬約束混合的優化問題[15]。上述工作是將代理模型應用到昂貴約束優化問題中的早期嘗試，通過對昂貴約束進行建模，減少算法的昂貴評估，使算法在可接受時間內完成對問題的優化。

雖然模型的使用提高了算法運行效率，但模型擬合的不準確性也降低了算法性能。為了提高SAEAs 在昂貴約束優化問題的求解質量，一些學者對模型管理策略進行研究，他們通過利用模型進行樣本選擇[16-18]、設計排序和修正策略[19-20]提高模型預測結果的可靠性及加入局部選擇和局部搜索[21-22]等策略來提高代理模型對約束的處理能力。上述工作聚焦于將多目標處理技術與代理模型有機結合，展現了SAEAs求解昂貴約束優化問題的巨大潛力。

然而，上述工作對所挑選的候選解都要進行所有約束的昂貴評估，導致耗費大量不必要的計算代價。在一些問題中，最優解往往被某個或某幾個約束的可行域限制，其他約束可行域非常大。在這種情況下，對每個挑選的候選解都真實評估可行域非常大的約束是不必要的；尤其當可行域大的約束數量較多的時候，對這些約束進行真實評估是浪費計算時間和有限評估次數的。因此，如何進行評估資源與昂貴約束的分配是影響算法性能的關鍵，直接關系到算法設計中兩個亟需解決的難點：

（1）個體的選擇。如何根據模型預測結果選擇對優化有幫助的個體進行昂貴評估，引導種群向優質區域演化。

（2）約束的選擇。如何選擇可行域信息較少的約束進行更多的評估和信息補充，加快算法對可行域的探索。

為解決評估資源與昂貴約束的分配問題，本文提出一種自適應約束評估策略，并從兩個思路出發，設計了兩種自適應約束評估的高斯過程回歸模型輔助差分進化算法，在少量昂貴評估下完成對問題的優化，驗證自適應約束評估策略的有效性和通用性。文章的主要貢獻點如下：

（1）提出一種自適應約束評估策略，自適應地根據種群信息進行個體選擇、約束選擇和昂貴評估。在演化過程中，并非對挑選候選解的所有約束進行昂貴評估，而是評估當前種群中可行域信息較少的約束，節省的評估次數可以用來進一步演化。因此，不同的候選解消耗的真實評估次數不同，并且隨著種群的演化而自適應動態變化。

（2）從代理模型輔助無約束演化方法思路出發，通過加入自適應約束評估策略和約束處理技術，設計一種自適應約束評估的約束優化高斯過程回歸模型輔助的演化算法。

（3）從無代理模型輔助的傳統約束優化演化算法思路出發，通過加入自適應約束評估策略和代理模型技術，設計一種自適應約束評估的代理模型輔助的復合約束差分進化算法。

在實驗方面，本文以約束優化問題標準測試集CEC2006 和四個工業應用為測試實例，驗證自適應約束評估策略及兩種自適應約束評估SAEAs的有效性，展示其在工業中良好的發展前景；在理論方面，本文從性能提升和效率提升兩方面進行分析，并對兩種自適應約束評估SAEAs進行對比分析。

1 相關工作

約束優化SAEAs主要由模型管理、演化算法、約束處理三部分組成，本章對昂貴約束優化問題和三個算法部分使用的方法作簡要介紹。

1.1 昂貴約束優化

通常情況下，一個單目標最小化約束優化問題可以由下式表達：

其中，x是一個D維變量，ld和ud分別是每一維的取值上下界；f(x)是目標函數，y是需要優化的目標值；G(x)是需要滿足的約束違反程度，由一個或多個不等約束和等式約束組成，其計算方法如下：

其中，g(x)是需要滿足的q個不等約束，h(x)是需要滿足的m-q個等式約束。一般情況下，g(x)≤0 表示x對于不等約束條件的滿足；h(x)=0 表示x對于等式約束條件的滿足。對于變量x，當且僅當滿足所有約束時，該變量稱為可行解，此時，約束違反程度G(x)≤0；若變量x違反至少一個約束，則該變量稱為不可行解，此時，約束違反程度G(x)＞0。

在一些現實問題中，f(x)和G(x)需要通過仿真軟件模擬甚至真實實驗獲得，計算代價是非常昂貴的。在這種情況下，用傳統EAs通過大量真實評估尋優所花費的時間代價非常大。為解決這個問題，代理模型被結合到演化過程中降低真實評估次數。由于模型的訓練和預測時長與真實評估相比可以忽略不計，這種方法能夠在可接受時間內獲得優化解，在解決昂貴優化問題中有廣泛應用。

1.2 高斯過程回歸

在SAEAs 演化過程中，后代質量的評估絕大部分依賴于模型。現有的SAEAs 大部分使用回歸模型，高斯過程回歸模型備受關注[6,23-25]。

高斯過程回歸模型是一種廣泛使用的監督學習模型[26]，它將多元高斯分布拓展到高維。假設一個含有n個樣本的D維數據集Y={f(x1),f(x2),…,f(xn)}，每個點都滿足高斯分布N(μ,σ2)，其中μ是期望，σ是標準差。不失一般性，假設μ=0。對數據集中的任意兩點x1和x2，它們之間的相關性僅依賴于x1-x2，即：

其中，參數pd∈[1,2]，控制每一維變量與f(x)的平滑度；θd＞0 控制每一維變量的權重；更多細節可以參照Rasmussen的文章[27]。

在求解最小化優化問題中，高斯過程回歸的結果一般取置信下界。假設預測結果滿足分布N(f′(x),s(x)2)，則該分布置信下界為：

其中，ω是一個常量，通常設置為2[28]。

由于高斯過程回歸模型的有效性，本文采取該模型作為輔助，分別對目標和每一個約束訓練一個高斯過程回歸模型；對于產生的候選解進行質量預測，根據自適應約束評估策略進行真實評估，并更新模型，以提高模型的訓練質量，更好地引導種群進化。

1.3 差分進化算法

演化算子是算法的核心部分，直接影響算法的探索和開發能力。本文采用一類基于群體的啟發式算法——差分進化算法[29-30]。

差分進化算法框架如圖1所示，包括變異、交叉、選擇。首先，算法開始前初始化參數及種群；然后，種群中每個個體通過變異操作產生變異個體；變異個體通過交叉操作產生試驗個體；最后，試驗個體作為后代與父代比較并選擇較好個體進入下一代。

圖1 差分進化算法框架Fig. 1 Framework of differential evolution algorithm

根據變異操作的不同，差分進化算法可分為不同的版本，本文涉及的進化算子有：

（1）DE/best/1

在交叉操作中，本文用到的是二項交叉來產生試驗個體，過程如下：

差分進化算法在解決傳統約束優化問題中應用非常廣泛，且求解效率和質量非常高[31-33]，本文使用該算法作為演化算子對搜索空間進行開發和探索。

1.4 約束處理技術

約束處理技術大致可以分為四類：基于懲罰函數的方法、基于支配準則的方法、基于多目標優化的方法和混合方法。下面介紹本文用到的基于懲罰函數的方法和基于支配準則的方法。

1.4.1 基于懲罰函數的方法

基于懲罰函數的方法是指將約束違反程度轉換為懲罰因子加到目標值上，將約束優化問題轉化為無約束優化問題。本文參照一種多目標約束優化問題中的基于懲罰函數的約束處理技術[34]，首先將目標值和約束值進行如下歸一化處理：

rf是當前種群的可行解比例。懲罰項目標值F(x)為：

根據上述計算公式可得，懲罰目標值F(x)能夠根據種群中可行解比例調整對目標和約束的側重。當種群中可行解個數較少時，懲罰目標值中約束所占比重較大，有利于種群繼續搜索可行域；當種群中可行解個數為0 時，懲罰目標值即個體約束值，種群只進行可行域的搜索。當種群中可行解個數較多時，懲罰目標值中目標所占比重較大，有利于種群開發可行域；當種群中所有個體均為可行解時，懲罰目標值即個體目標值，種群只進行目標的優化。由于該方法能夠調整對目標和約束的演化側重，并且在求解約束問題中有較好的性能表現[34]，本文選擇該方法作為一種約束處理技術。

1.4.2 基于支配準則的方法

基于支配準則的約束處理方法主要有可行解支配準則和ε約束支配準則。可行解支配準則內容為：（1）可行解優于不可行解；（2）同為不可行解，約束違反程度小的個體優于約束違反程度大的個體；（3）同為可行解，目標值好的個體優于目標值劣的個體。由此可見，可行解支配準則傾向于保留可行解，不能有效利用目標值有重要意義的不可行解，不利于處理某些最優解在可行域邊緣的問題。ε約束支配準則對其改進，根據種群進化情況可以自適應地調整對不可行解的保留程度：對于兩個不同的個體，滿足下列關系之一時，x1優于x2：

其中，ε0是初始種群的最大約束違反程度，T是最大進化代數，t是當前進化代數，λ是常數，設置為6；p是控制目標值開發的參數，設置為0.5。由于考慮了可行域周圍的不可行解，ε約束支配準則能夠有效利用目標值較好的不可行解幫助對可行域的探索。

可行解支配準則能夠綜合目標值和約束值對個體進行最直接的優劣排序，是求解約束優化問題中最常用的方法之一[3,21,32-33]，因此本文選擇該方法作為一種約束處理技術。

2 自適應約束評估策略

在設計約束優化SAEAs 時，核心問題是個體選擇和約束處理，本文提出一種新的自適應約束評估策略，其具體實現過程如算法1所示。

算法1自適應約束評估策略偽代碼

在自適應約束評估策略中，除維護一個全部真實評估個體數據集DBf之外，還需維護一個部分真實評估個體數據集DBp，用來保存部分約束完成真實評估、部分約束只有預測值的個體。相對應地，該策略主要包括兩部分，部分評估個體選擇和全部評估個體選擇。自適應約束評估策略的步驟如下：

首先，判斷當前代數需進行哪一種選擇。若當前代數需進行部分評估個體選擇，在產生的后代中選擇被預測為支配最優的個體，并初始化需進行真實評估的約束集合J為空。針對每一個約束j，按照式（21）計算當前種群在該約束可行域比例r，其中，Nfea是種群在該約束可行域內的個體數量，NP是種群大小。

同時，設置需進行真實評估的約束可行比例閾值thr=0.5。若r＜thr，則將該約束的索引加入到需真實評估的約束索引集合J中；否則不需加入。對所有約束判斷完之后，將所選個體xsel按索引集合J進行真實評估，未進行真實評估的約束保留預測值。由此，該個體便成為了部分評估個體，被加入到部分評估個體數據集DBp，更新已消耗的真實評估次數fes。

若當前代數需進行全部評估個體選擇，則從DBp中根據1.4.1小節的懲罰函數方法挑選最優的部分評估個體，標記該個體未被真實評估的約束，對這些約束及目標進行真實評估。由此，該個體便成為全部評估個體，從DBp中刪除并加入到全部評估個體數據集DBf，更新消耗的真實評估次數fes。

在自適應約束評估策略中，需進行信息補全的代數Gap是一個重要的參數，它決定著算法進行種群和代理模型更新的頻率。Gap值越大，算法要消耗越多的真實評估次數來進行部分約束評估，導致種群和代理模型更新緩慢，有效演化大大減少；極端情況下，當Gap值大到種群完全沒有信息補全，則算法終止后沒有任何全部評估的新個體產生，無法得知DBp中是否有更好的解，這種無效優化是不可取的。Gap值越小，種群和代理模型更新越快，導致算法在可行域信息較多的約束上頻繁消耗昂貴評估，不能在可行域信息較少的約束上節省真實評估次數而使種群進行更多代演化；特別地，當Gap值為1 時，與大多數約束優化SAEAs 一致，算法對每個被選擇的個體進行所有約束和目標值的真實評估。因此，Gap值的設置對算法的演化影響較大，如何對該變量進行合適設置有待于進一步研究。在本文中，由于真實評估次數較少，且測試問題的約束數量不同，根據實驗性能設置Gap=10。

自適應約束評估策略的自適應特性主要體現在對約束選擇方面。與其他約束處理不同，自適應約束評估策略旨在對不同約束進行區別對待，僅對可行域信息較少的約束進行真實評估，即計算當前種群在每個約束的可行域比例，當且僅當該比例小于閾值thr時，選擇該約束進行昂貴評估。thr是一個重要的參數，根據4.3節參數調研結果設置；同時，參數調研實驗顯示，在演化前期，不能達到閾值thr的約束較多，這些約束均被選擇進行昂貴評估；隨著演化的進行，種群逐漸掌握更多可行域信息，達到閾值thr的約束較多，被選擇進行昂貴評估的約束變少；當種群完全在可行域內時，在每個約束的可行域比例均為1，不需要選擇約束進行昂貴評估。因此，在整個演化過程中，被選擇進行昂貴評估的約束是一個自適應變化的過程。

另外，為了掌握所選解的全部約束及目標信息，提高種群掌握信息的準確性和更新訓練代理模型，每隔Gap代進行全部評估個體選擇，從部分真實評估個體數據集DBp中選擇個體進行信息補全，即真實評估仍保留的預測值信息；該選擇基于1.4.1 小節所描述的基于懲罰函數的方法，目的是使算法根據當前種群的可行域信息調整對目標和約束的演化側重。

3 自適應約束評估的約束優化SAEAs

3.1 框架

本文提出了一種自適應約束評估策略，并從兩個思路出發設計了兩種基于自適應約束評估策略的約束優化SAEAs。

思路1從無約束SAEAs 出發，通過加入約束處理技術和自適應約束評估策略，設計一種基于自適應約束評估策略的約束優化算法，詳見3.2節。

思路2從約束優化EAs 出發，通過加入高斯過程回歸模型輔助和自適應約束評估策略，設計一種基于自適應評估策略的代理模型輔助約束優化算法，詳見3.3節。

這兩種基于自適應約束評估策略的約束優化SAEAs 流程框架如圖2 所示。首先用拉丁超立方采樣（Latin hypercube sampling，LHS）初始化樣本作為已知數據并加入數據庫DBf中；在算法終止前，從DBf中按照可行解支配準則選取最優的NP個個體組成種群，通過演化算子產生后代；用DBf中最優的NT個數據訓練目標和約束模型，并對后代進行預測；按照自適應約束評估策略進行個體選擇、約束選擇和昂貴評估，并將個體加入到相對應的數據庫中；算法終止時，輸出DBf中最優結果。兩種算法的具體內容如下。

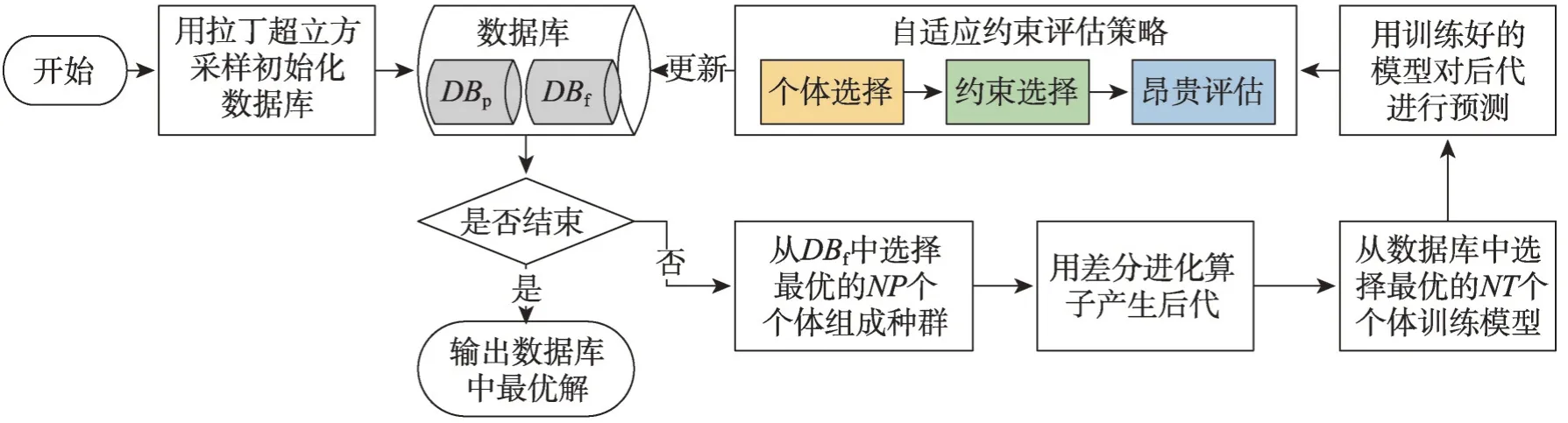
圖2 自適應約束評估的約束優化SAEAs框架Fig. 2 Framework of adaptive constraint evaluation aided SAEAs for expensive constrained optimization

3.2 自適應約束評估的約束優化GPEME

本節從基于代理模型輔助的單目標優化方法（Gaussian process surrogate model assisted evolutionary algorithm，GPEME）[7]出發，通過加入約束處理技術和自適應約束評估策略，設計一種自適應約束評估策略的約束優化GPEME（D-GPEME-CH），具體過程如下：

（1）用LHS 從搜索空間中隨機采樣NT個樣本，進行真實評估后加入數據庫DBf中。

（2）判斷是否達到終止條件，若達到終止條件，則停止算法并輸出數據庫DBf中最優解；否則跳到第（3）步執行。

（3）選擇DBf中支配最優的NP個個體組成種群。

（4）對種群應用DE/best/1算子產生后代。

（5）選擇數據庫中支配最優的NT個個體組成訓練集，對目標和每個約束各訓練一個高斯過程回歸模型。

（6）用訓練好的模型對種群產生的后代進行目標和約束值預測，并執行自適應約束評估策略，更新對應數據庫。

在D-GPEME-CH 中，DE/best/1 是全局搜索能力很強的差分進化算法，能夠有效開發已知最優區域；自適應約束評估策略能夠使算法在可行域較大的約束上節省昂貴評估，在可行域較小的約束進行更多的信息探索，加強對可行域的探索。在高斯過程回歸模型的輔助下，該算法能夠有效求解昂貴單目標約束優化問題。

3.3 自適應約束評估的代理模型輔助C2oDE

本節從傳統單目標復合差分進化約束優化算法（composite differential evolution for constrained optimization，C2oDE）[33]出發，通過加入代理模型輔助技術和自適應約束評估策略，設計一種自適應約束評估策略的代理模型輔助C2oDE（surrogate-assisted C2oDE with adaptive constraint evaluation,D-SA-C2oDE），具體過程如下：

（1）使用LHS 從搜索空間中隨機采樣NT個點，進行真實評估后加入數據庫DBf中。

（2）判斷是否達到終止條件，若達到終止條件，則停止算法并輸出數據庫中最優解；否則跳到第（3）步執行。

（3）選擇DBf中支配最優的NP個個體組成種群。

（4）對種群使用復合差分進化算子C2oDE 產生后代，即每個個體使用DE/current-to-rand/1、DE/randto-best/1和DE/current-to-best/1三種差分算子進行演化，擁有三個子代個體。

（5）選擇數據庫中支配最優的NT個個體組成訓練集，對目標和每個約束各訓練一個高斯過程回歸模型。

（6）對于每個個體產生的三個子代個體，基于高斯過程回歸模型的預測目標值和約束值，根據可行解支配準則進行預篩選，保留最好的個體作為后代。

（7）在預篩選的后代中，執行自適應約束評估策略并更新對應數據庫。

在D-SA-C2oDE中，復合差分進化算子DE/currentto-rand/1 能夠提高種群多樣性；DE/rand-to-best/1 和DE/current-to-best/1能夠提高種群的收斂速度。可行解支配準則在對后代進行預篩選時，能夠取優去劣；ε約束支配準則在對后代進行選擇時，能夠隨著進化程度自適應調整是否保留可行域邊緣的不可行解。因此，該算法在自適應約束評估策略和高斯過程回歸模型的輔助下能夠在可接受時間內對昂貴約束優化問題進行有效求解。

4 實驗與分析

本章首先對測試問題進行介紹，說明兩種算法參數設置情況；然后通過實驗展示自適應約束評估策略的有效性，并在CEC2006 測試集和四個工業優化問題中進行對比實驗并分析結果，展示本文設計的兩種算法性能；最后從理論方面對性能提升和效率提升進行分析，并對本文從兩個思路設計的自適應約束評估SAEAs進行對比分析。

4.1 測試問題簡介

CEC2006 是一個單目標約束優化問題標準測試集，包含24個問題，每個問題的維度及約束個數都不相同，具有大部分工業約束優化問題的特征[35]，如表1所示。其中，ρ是可行域占整個搜索空間的比例，0.000 0%表示該問題的可行域相對于整個搜索空間的比例小于0.000 1%；LI是線性不等約束個數，NI是非線性不等約束個數；LE是線性等式約束個數，NE是非線性等式約束個數；a指在可行域最優解附近比較活躍的約束個數，該值越大，表示待優化問題的最優值受約束的影響越大。

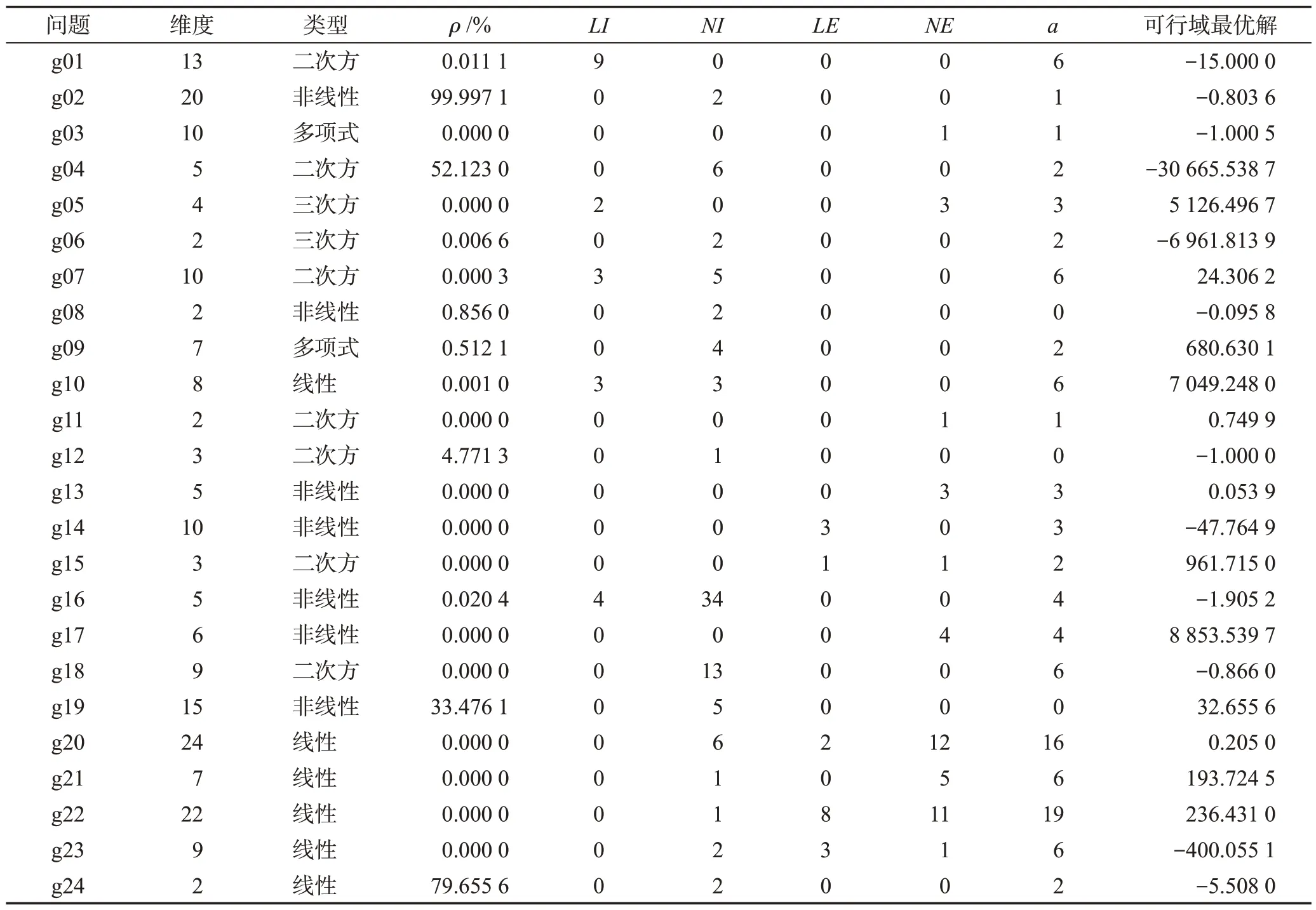
表1 CEC2006測試問題Table 1 CEC2006 benchmark functions

本文測試的工業優化問題包括4個：碟形彈簧設計優化（belleville spring design,BS）、散貨船設計優化（bulk carrier design,BCD）、轎車側面碰撞優化（car side impact design,CSI）和螺旋彈簧設計優化（helical spring design,HS）。BS是一個帶有7個不等約束的4維優化問題，BCD是一個帶有9個不等約束的6維優化問題，CSI是一個帶有10個不等約束的11維優化問題，HS是一個帶有9個不等約束的3維優化問題，詳細問題介紹可以在文獻[36]中找到。目前，這4個問題都沒有已知最優可行解。

4.2 參數設置

算法開始前初始化樣本量為300；高斯過程回歸模型訓練集大小NT=300，種群大小NP=50。經參數調研，需進行真實評估的約束可行比例閾值thr=0.5。在D-GPEME-CH中，DE/best/1演化算子的變異概率F=0.8，交叉概率CR=0.8 。在D-SA-C2oDE 中，差分進化算子的變異概率F和交叉概率CR通過參數調研設置為F=0.6，CR=0.7。需注意的是，對目標或約束的單獨評估即為消耗一次評估次數。由于對比算法C2oDE 的原文設置種群大小為50，且每一代對產生的50×3個后代進行真實評估[33]，若按無約束優化SAEAs[7-8]中常設置的最大評估次數maxFES=1 000，則在該算法中，種群進化代數為1 000/(50×3×(NC+1))，約為7/(NC+1)，其中NC為該測試問題的約束個數。然而，由表1中測試問題的約束個數可得，在該設置下，大多數問題僅能演化非常少的代數，有的問題甚至無法完成一代演化，使算法無法對問題進行有效求解。因此，本文設置maxFES=1 000×(NC+1)，即最大評估次數由問題的約束個數決定，不同問題的終止條件不同。這個設置是合理的，約束多的問題，可行域較復雜，優化過程相對困難，因此最大評估次數較多；相反，約束少的問題，可行域較簡單，優化過程相對容易，因此最大評估次數較少。為保證實驗公平性，所有結果均取自25次獨立實驗的均值。

4.3 參數調研

為調研參數設置合理性，本節調研不同的取值對需進行真實評估的約束可行比例閾值thr和D-SAC2oDE 中差分進化算子的變異概率F、交叉概率CR的影響。不失一般性，本節以函數g01、g02、g06、g07、g09、g19為例，由表1可知，此6個函數能夠代表不同類型、不同約束數量的函數。

需進行真實評估的約束可行解比例閾值thr是自適應評估策略中一個重要的參數，它決定著演化過程中哪些約束需要進行真實評估。對于每一個約束，若種群在該約束的可行域個體比例大于thr，則認為種群大部分處于該約束的可行域內，不需要頻繁對該約束進行昂貴評估；相反，若種群在該約束的可行域個體比例小于thr，則認為種群大部分處于該約束的不可行域內，需要對該約束進行昂貴評估觀察其演化方向。為調研該參數的取值對實驗結果的影響，設置thr={0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}，在D-GPEME-CH 和D-SA-C2oDE 兩種方法分別進行實驗并對比分析結果，實驗結果如圖3所示。

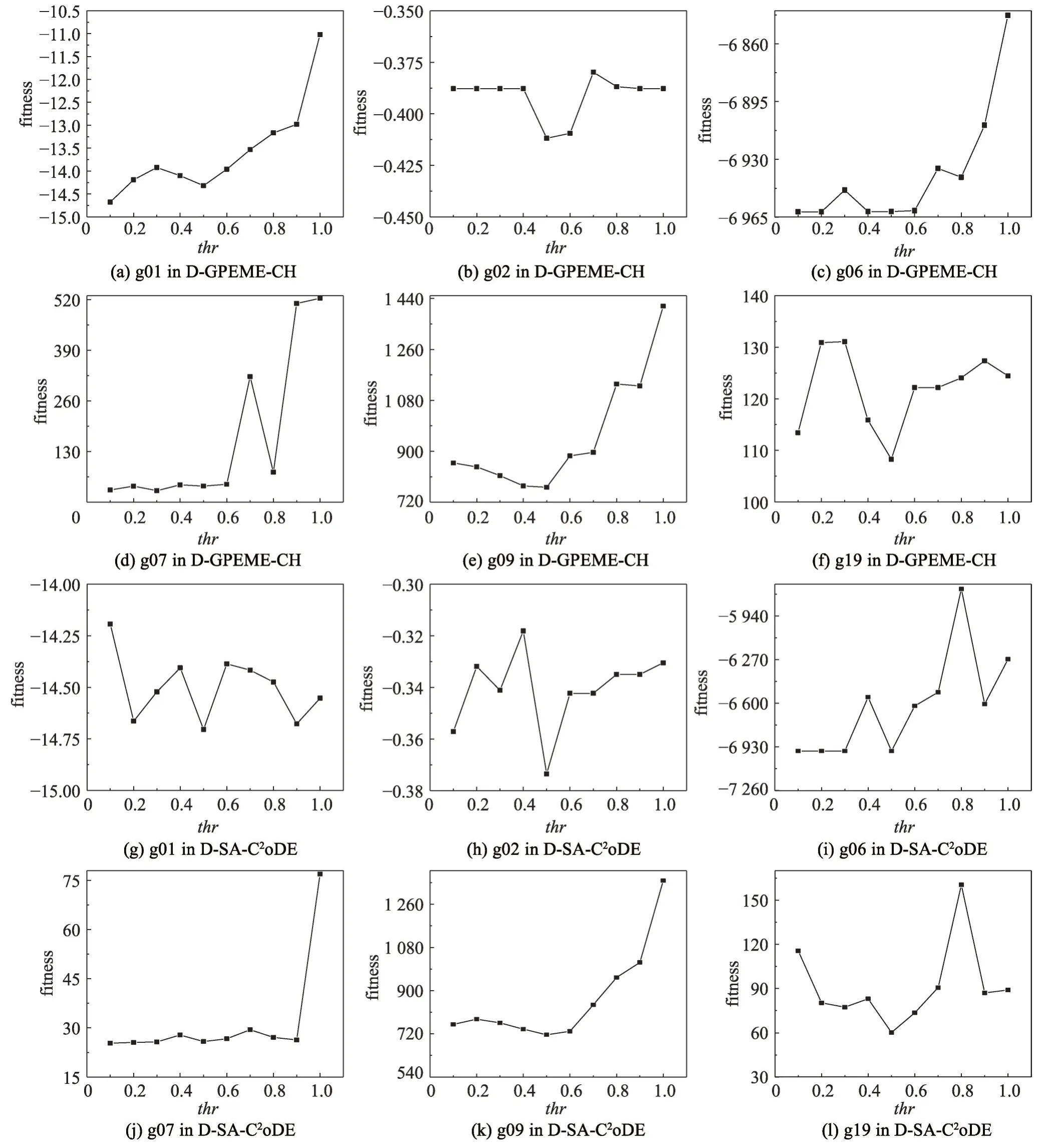
圖3 thr不同取值對實驗結果的影響Fig. 3 Influence of different values of thr on results

圖3 中橫軸為thr不同的取值，縱軸為對應取值獲得的適應值。從圖中可以看出，兩種算法在不同的函數中呈現出大致相同的規律，當thr＜0.5 時，適應值隨著thr的增大而變好；當thr＞0.5 時，適應值隨著thr的增大而變差。這個現象是合理的，thr較小時，昂貴評估的約束較少；極端情況下，若thr=0，則所有約束都不被昂貴評估，難以在演化過程較快尋找到可行域。thr較大時，昂貴評估的約束較多；極端情況下，若thr=1，則所有約束都被昂貴評估，在昂貴評估次數有限的情況下，對昂貴評估造成浪費，限制了算法的進一步演化。結合實驗結果與分析，本文設置thr=0.5。為進一步說明自適應評估策略的自適應特性，以g01 和g07 為例，用D-GPEME-CH 測試在thr=0.5 的演化中可行約束個數的變化情況，實驗結果如圖4。由于算法在少量評估次數內就找到所有約束的可行域，為方便觀察，橫坐標只繪制最大評估次數為1 000。

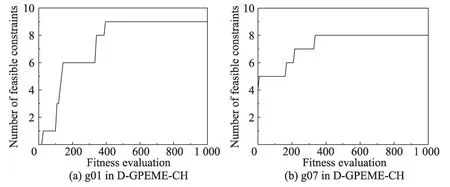
圖4 演化過程找到可行約束的個數Fig. 4 The number of found feasible constraints during evolution

圖4中，g01是一個帶有9個約束的函數，在算法演化初期沒有任何約束的可行域信息被搜索到；隨著算法的演化，找到可行域信息的約束個數逐漸增加，在400 多次昂貴評估時，所有約束的可行域都被找到。g07 是一個帶有8 個約束的函數，其中4 個約束的可行域比較大，在算法初期就已經被找到；隨著算法的演化，找到可行域信息的約束個數逐漸增加，在400 多次昂貴評估時，所有約束的可行域都被找到。因此，thr=0.5 是一個比較合理的設置，能夠體現自適應評估策略的自適應特性。

在文獻[33]中，變異概率F建議以相等概率從{0.6,0.8,1.0}取值，交叉概率CR建議以相等概率從{0.1,0.2,1.0}取值。為進一步調研在D-SA-C2oDE 中差分進化算子的變異概率F、交叉概率CR的不同取值對實驗結果的影響，首先固定CR以相等概率從{0.1,0.2,1.0}取值的設置，對比F={0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}與F以相等概率從{0.6,0.8,1.0}取值的結果，如圖5 所示。圖5 中，橫軸為F不同的取值，縱軸為對應取值獲得的適應值，紅色虛線為F以相等概率從{0.6,0.8,1.0}取值的結果。從圖中可以得出，在加入自適應評估策略后，F=0.6 時的實驗結果比較好，因此本文設置F=0.6。

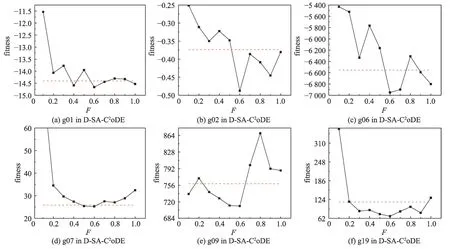
圖5 F不同取值對實驗結果的影響Fig. 5 Influence of different values of F on results

固定F=0.6 后，本文對比CR={0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}與CR以相等概率從{0.1,0.2,1.0}取值的結果，如圖6 所示。圖6 中，橫軸為CR不同的取值，縱軸為對應取值獲得的適應值，紅色虛線為CR以相等概率從{0.1,0.2,1.0}取值的結果。從圖中可以得出，在g06 中，CR以相等概率從{0.1,0.2,1.0}取值的結果較好；在多數其他測試函數中，CR=0.7 時的實驗結果比較好，因此本文設置CR=0.7。

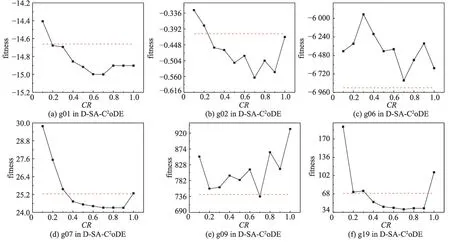
圖6 CR不同取值對實驗結果的影響Fig. 6 Influence of different values of CR on results

4.4 實驗結果

本節首先驗證復合差分進化算法和自適應約束評估策略的效果；然后對比從兩個思路設計的自適應約束評估SAEAs在標準測試集CEC2006中的尋優情況，以驗證SAEAs相對于傳統EAs的性能提升，并以四個函數為例進行時間結果的統計與分析；最后在四個工業約束優化問題中進一步驗證自適應約束評估SAEAs的求解質量和效率。

4.4.1 復合差分進化算子性能驗證

為驗證復合差分進化算子的性能，本小節以函數g01、g02、g19 為例，比較獨立差分進化算子DE/current-to-rand/1、DE/rand-to-best/1 和DE/current-tobest/1與復合差分進化算子的實驗結果。相對應地，上述算法分別命名為D-SA-DEc2r、D-SA-DEr2b、DSA-DEc2b、D-SA-C2oDE。算法收斂結果如圖7所示。

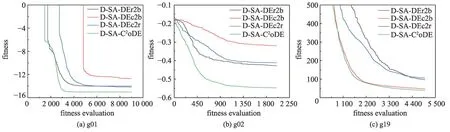
圖7 差分進化算子對實驗結果的影響Fig. 7 Influence of different DEs on results

圖7中橫軸為消耗的昂貴評估次數，縱軸為算法尋優的適應值。可以看到，復合差分進化算子的DSA-C2oDE 收斂速度更快，且收斂效果更好。這是因為獨立差分進化算子的D-SA-DEr2b、D-SA-DEc2b在最優個體的引導下容易陷入局部最優，而D-SADEc2r雖然隨機性比較大，但沒有最優個體的引導難以往全局最優方向收斂。復合差分進化算子結合了三種算子的特點，既能夠保證種群的收斂性，又能夠提高種群多樣性，幫助種群跳出局部最優，往全局最優的方向收斂。因此，復合差分進化算子能夠提高種群多樣性，并加快收斂速度，提高收斂效果。

4.4.2 自適應約束評估策略性能驗證

為驗證自適應約束評估策略的效果，本小節對比從兩種思路設計的自適應約束評估SAEAs（DGPEME-CH、D-SA-C2oDE）及不帶該策略的SAEAs（GPEME-CH、SA-C2oDE）實驗結果。其中，GPEMECH、SA-C2oDE 按照1.4.1 小節選擇懲罰適應值最優的個體進行昂貴評估。所有算法真實評估次數均為1 000×(NC+1)，算法25 次獨立運行所得結果如表2所示。均值是指25 次獨立實驗最優解的均值，方差是指25 次獨立實驗最優值的方差。“NaN”表示算法在25次實驗中均未找到可行解。

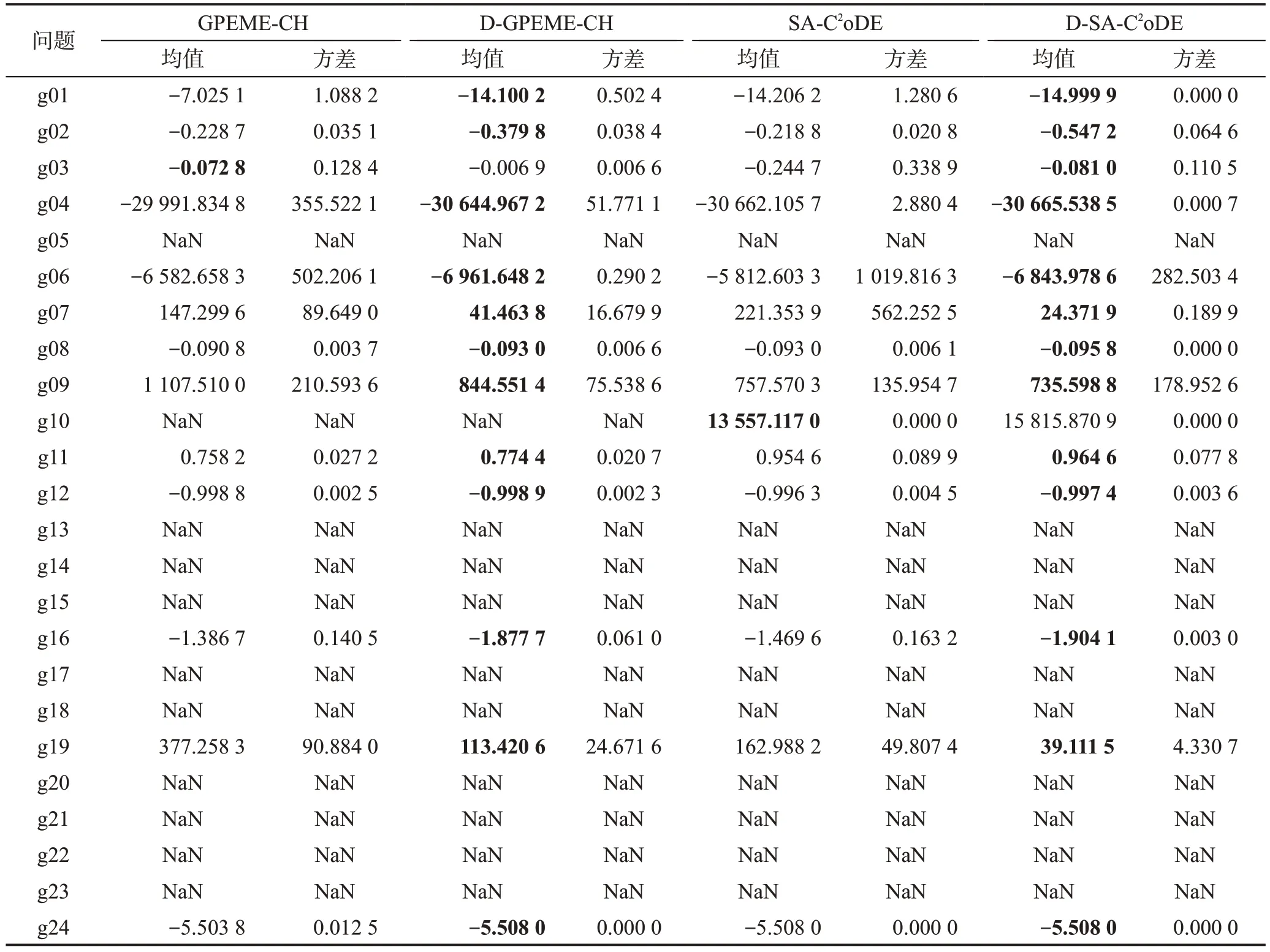
表2 自適應約束評估策略性能驗證對比結果Table 2 Comparison results to validate effectiveness of adaptive constraint evaluation strategy

從表2 中可以看到，加入自適應約束評估策略后，兩種思路設計的約束優化SAEAs 性能均有所提升。在無自適應約束評估策略的算法中，每一代選擇的候選解要進行所有約束和目標值的真實評估，消耗的真實評估次數較多，限制了種群演化代數。而自適應約束評估策略僅對需要的信息進行評估，節省的評估次數可以用來進一步演化種群。因此，在自適應約束評估策略的輔助下，算法性能能夠有進一步提升。

需注意的是，在測試函數g05、g13、g14、g15、g17、g20、g21、g22、g23 中，算法無法找到可行解。從表1函數性質可得，這些函數均含有多個等式約束。一方面，等式約束在變量空間形成的可行域是一個超平面、平面、一條線甚至一個點，如此復雜的函數特性對于代理模型來說是很難擬合的；另一方面，代理模型通過對后代預測輔助種群演化，而等式約束形成的可行域是一個精細化的點線面，用一個近似的模型去預測一個精細化的函數是不現實的。因此，如何對昂貴等式約束有效處理仍有待研究，在下面的實驗中，不對上述函數進行分析討論。

為說明自適應評估策略的自適應特性，以及自適應約束評估策略在減少評估次數的情況下對算法精度的影響，首先，以g01和g07為例，測試自適應約束評估策略的算法D-GPEME-CH和所有約束評估策略的算法GPEME-CH在演化過程中可行約束個數的變化情況，實驗結果如圖8。由于算法在少量演化代數內就找到所有約束的可行域，為方便觀察，橫坐標只繪制到演化代數為100。

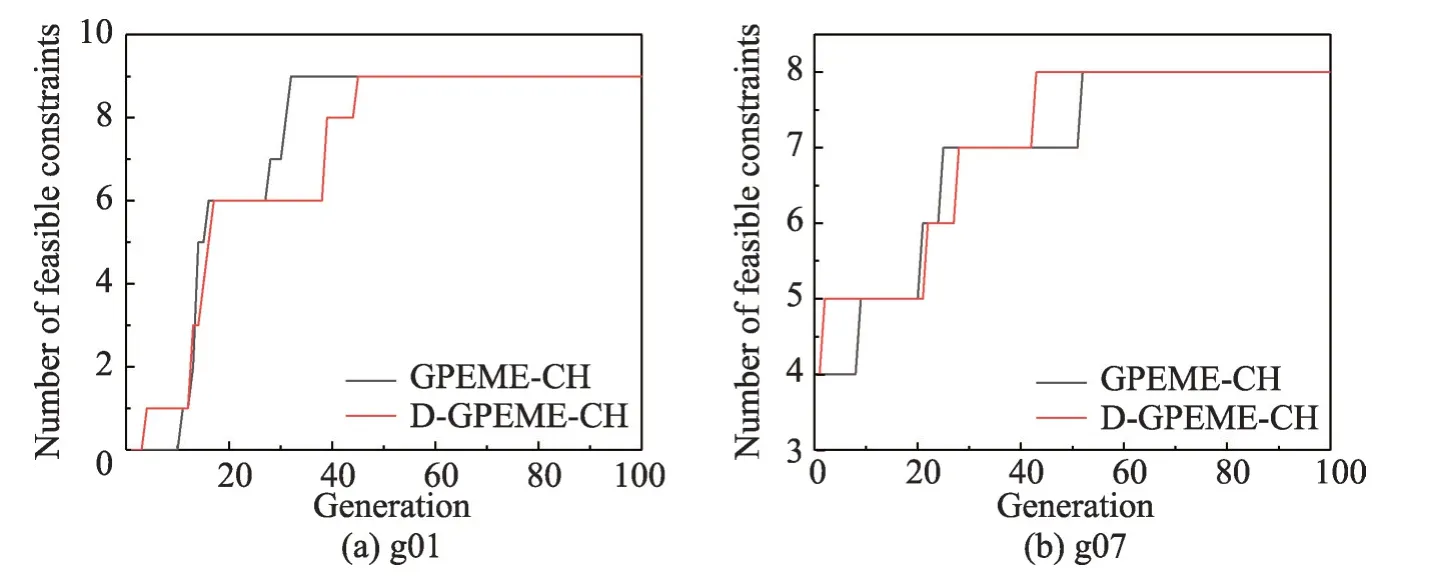
圖8 約束評估策略對約束演化效果調研Fig. 8 Influence investigation of different constraint evaluation strategies on constraints exploration

圖8中，g01是一個帶有9個約束的函數，在算法演化初期沒有任何約束的可行域信息被搜索到；g07是一個帶有8個約束的函數，其中4個約束的可行域比較大，在算法初期就已經被找到。隨著算法的演化，兩種策略均能在60 代演化內找到所有約束的可行域，雖然自適應約束評估策略在相同的演化代數減少昂貴評估次數，但對算法找到所有約束可行域的影響不大，這是因為在自適應約束評估策略中，種群在約束可行域比例大于thr表明種群已大部分進入該約束的可行域內，無需頻繁對其進行昂貴評估尋找可行域；相反，種群在約束可行域比例小于thr表明種群大部分在該約束的可行域外，需要通過昂貴評估引導演化方向，探索可行域。因此，自適應約束評估策略節省的是種群掌握大部分可行域信息約束的昂貴評估次數，對算法進入可行域的速度并沒有太大的影響，但節省的昂貴評估次數可以用來進一步演化，增加演化代數，使算法找到更優的解。

為進一步分析自適應約束評估策略與對所有約束進行昂貴評估策略對算法性能的影響，本文以函數g01、g02、g06、g07、g09、g19為例，分析演化代數相同和昂貴評估次數相同兩種情況下自適應約束評估策略與對所有約束進行昂貴評估方式對算法性能的影響。設置演化代數為1 000，此時若對所有約束進行昂貴評估，昂貴評估次數為1 000×(NC+1)；若執行自適應約束評估策略，昂貴評估次數小于等于1 000×(NC+1)。因此，在演化代數相同的情況下，自適應約束評估策略可以減少昂貴評估次數。為保證比較結果的公平性，進一步比較在昂貴評估次數相同的情況下自適應約束評估策略算法的性能。實驗結果如表3所示。

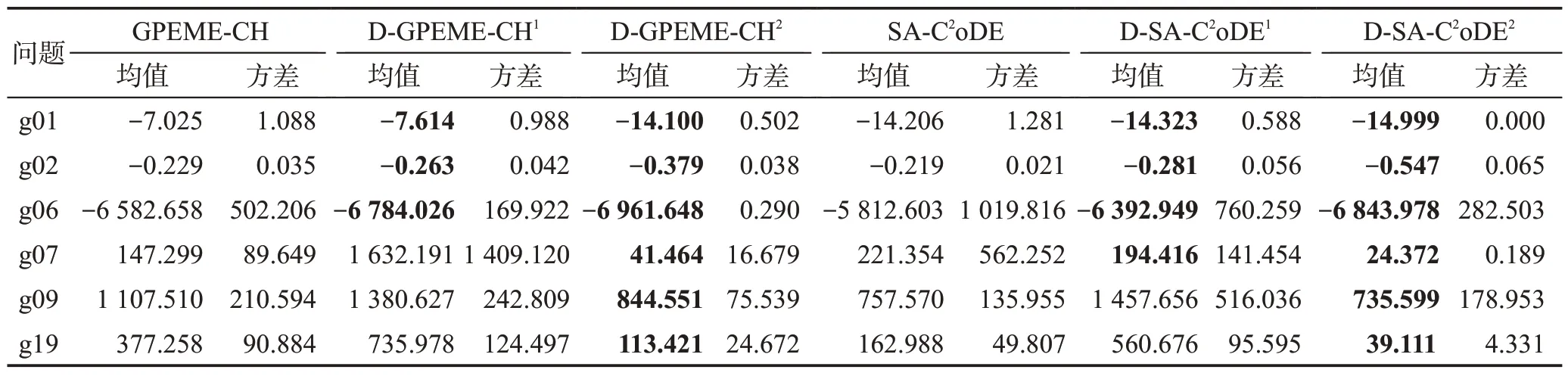
表3 自適應約束評估策略性能調研Table 3 Influence investigation of adaptive constraint evaluation

表3 中，上標“1”代表自適應約束評估策略的SAEAs 演化代數與所有約束評估策略的SAEAs相同，均為1 000；上標“2”代表自適應約束評估策略的SAEAs昂貴評估次數與所有約束評估策略的SAEAs相同，均為1 000× (NC+1)。從表中結果可以看到，演化代數相同的情況下，自適應約束評估策略的SAEAs并沒有在所有測試問題中比所有約束評估策略的SAEAs效果好。這是因為自適應約束評估策略的SAEAs在每一代中是自適應地進行約束選擇和昂貴評估，在一定的部分約束評估個體積累之后才進行個體選擇并補全真實約束值和目標值。相比所有約束評估策略的SAEAs，自適應約束評估策略的SAEAs 對所選解真實信息的掌握有一定的延遲，演化受到預測誤差的影響。在演化代數相同的情況下，自適應約束評估策略的SAEAs 所花費的昂貴評估次數有所減少。當自適應約束評估策略的SAEAs的昂貴評估次數和所有約束評估策略的SAEAs相同時，效果均有明顯提升。這是因為自適應約束評估策略可以減少對可行域信息較多的約束的頻繁評估，節省的昂貴評估次數可以用來進一步演化。因此，自適應約束評估策略的SAEAs能夠有效提升算法性能。

4.4.3 自適應約束評估的SAEAs性能驗證

昂貴優化是一個具有挑戰性研究方向的原因之一是真實評估次數非常少。為驗證SAEAs在求解昂貴優化問題相對于傳統EAs的性能優勢，本小節對傳統約束優化算法（C2oDE）和本文設計的兩種自適應約束評估的SAEAs（D-GPEME-CH、D-SA-C2oDE）在CEC2006 中25 次獨立運行結果作對比分析，算法優化的最優解如表4所示，算法結束時的可行解情況如表5 所示。由于在上一小節已經分析了代理模型處理昂貴等式約束的困難和在此領域的研究空白，這一小節不對帶有多個等式約束的函數進行測試分析。

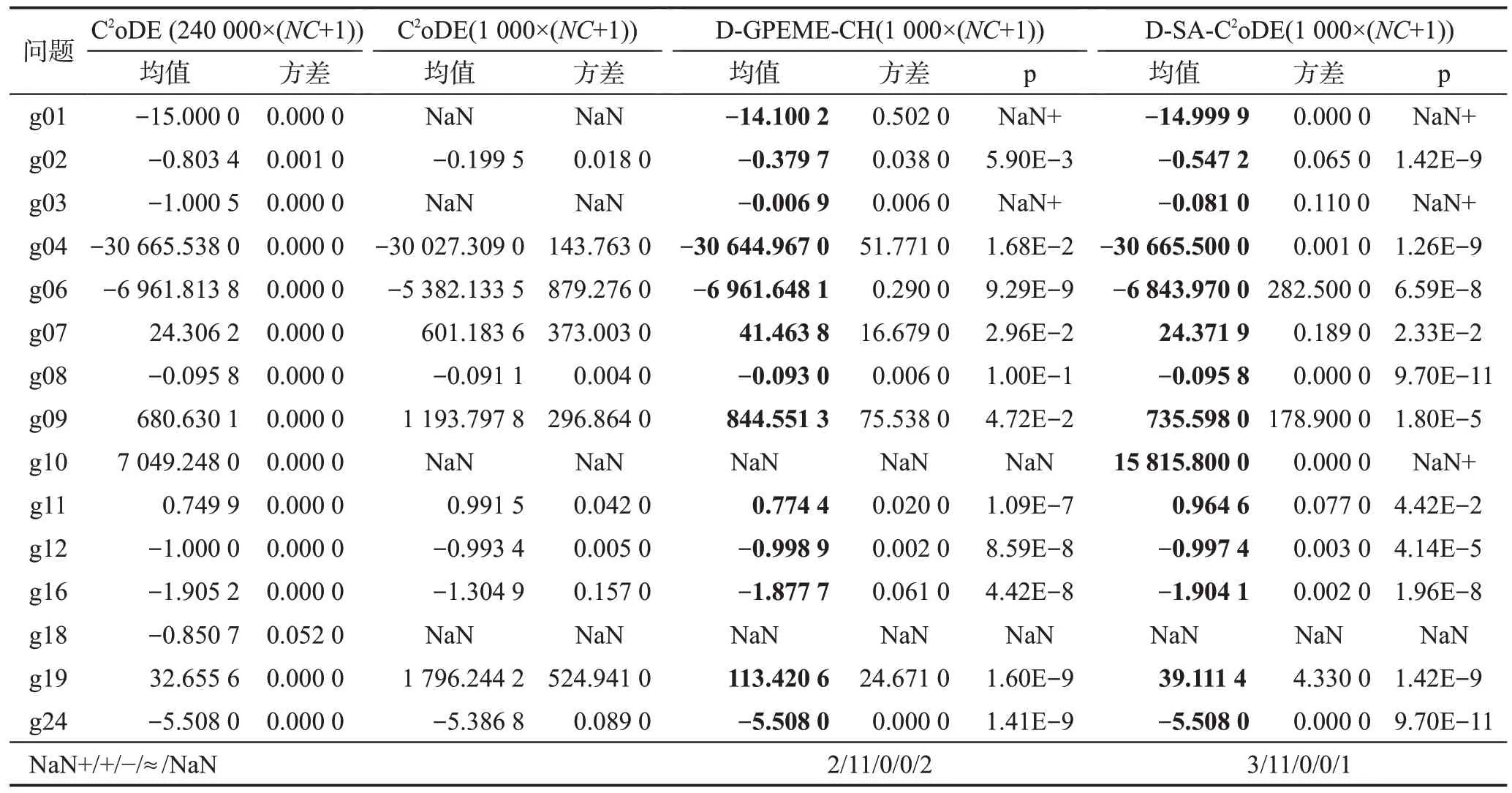
表4 自適應約束評估的約束優化SAEAs性能對比結果Table 4 Comparison results to validate effectiveness of adaptive constraint evaluation aided SAEAs for expensive constrained optimization

表5 CEC2006測試問題的可行解對比結果Table 5 Comparison results of feasibility in CEC2006

在表4中，p表示自適應約束評估SAEAs與C2oDE威爾克遜秩和檢驗的結果，+/-/≈表示顯著水平為0.05 的情況下，對應SAEAs 比C2oDE 尋優結果顯著好、顯著差和無明顯差異的次數。NaN+表示C2oDE無法找到可行解，而自適應約束評估SAEAs 可以找到可行解，此時無法進行統計學檢驗，但后者性能明顯優于前者。NaN 表示C2oDE 和自適應約束評估SAEAs 均未找到可行解，無法進行統計學檢驗和算法性能比較。表5中rf是算法結束時種群中的可行解比例在25 次獨立運行的均值；rs指所有運行中算法在結束時成功找到可行解的比例。C2oDE（240 000）指算法適應值評估次數為240 000×(NC+1)次，即原文設定的最大評估次數[33]；由于評估代價昂貴，本文設計的D-GPEME-CH 和D-SA-C2oDE 最大評估次數為1 000×(NC+1)，并將算法C2oDE 最大評估次數設置為1 000×(NC+1)進行實驗，以保證實驗的公平性，比較在有限次真實目標和約束評估次數下算法性能。

綜合表4 和表5 的結果可知，C2oDE（240 000）在真實評估次數非常多的時候，能夠在15 個測試問題中找到最優解，并且在所有問題中都能找到可行解且算法結束時種群中可行解比例為1。為公平比較，將該算法最大評估次數調整為1 000×(NC+1)后，算法性能急劇下降，在4個問題中無法找到可行解且在找到可行解的問題中求解質量不高。然而表4 顯示自適應約束評估SAEAs 求解質量有明顯提高，在15個測試函數中，D-GPEME-CH 和D-SA-C2oDE 均在11個函數中顯著優于相同評估次數的C2oDE；在g01和g03 中，C2oDE 無法找到可行解，而D-GPEME-CH和D-SA-C2oDE均能找到質量較好的可行解。同時，表5結果顯示，D-GPEME-CH和D-SA-C2oDE找到可行解的運行次數和在算法結束時種群的可行解比例普遍比C2oDE 高。由此可見，D-GPEME-CH 和DSA-C2oDE在有限目標和約束的真實評估次數內能夠取得較好的可行解，在自適應約束評估策略和代理模型的輔助下，比傳統EAs效果更好。

為進一步說明本文設計的兩種算法相對于其他求解昂貴約束優化問題算法的性能優勢，本文以近兩年提出的代理模型輔助的部分評估演化算法（surrogateassisted partial-evaluation-based EA，SParEA）[37]、代理模型輔助的分類協同差分進化算法（surrogate-assisted classification-collaboration DE，SACCDE）[38]為對比算法，在上述CEC2006 測試問題中進行對比分析；另外，為了測試本文設計的兩種算法在較高維問題中的性能優勢，本文增加在標準測試集CEC2010[39]的30維問題的測試。正如在4.4.1小節中提到的昂貴等式約束處理的難度和當前在此方面研究的空白，只測試CEC2010中不含等式約束的問題c01、c07、c08、c13、c14、c15。為保證實驗公平性，測試算法的最大評估次數均設置為1 000×(NC+1)，實驗結果如表6所示。

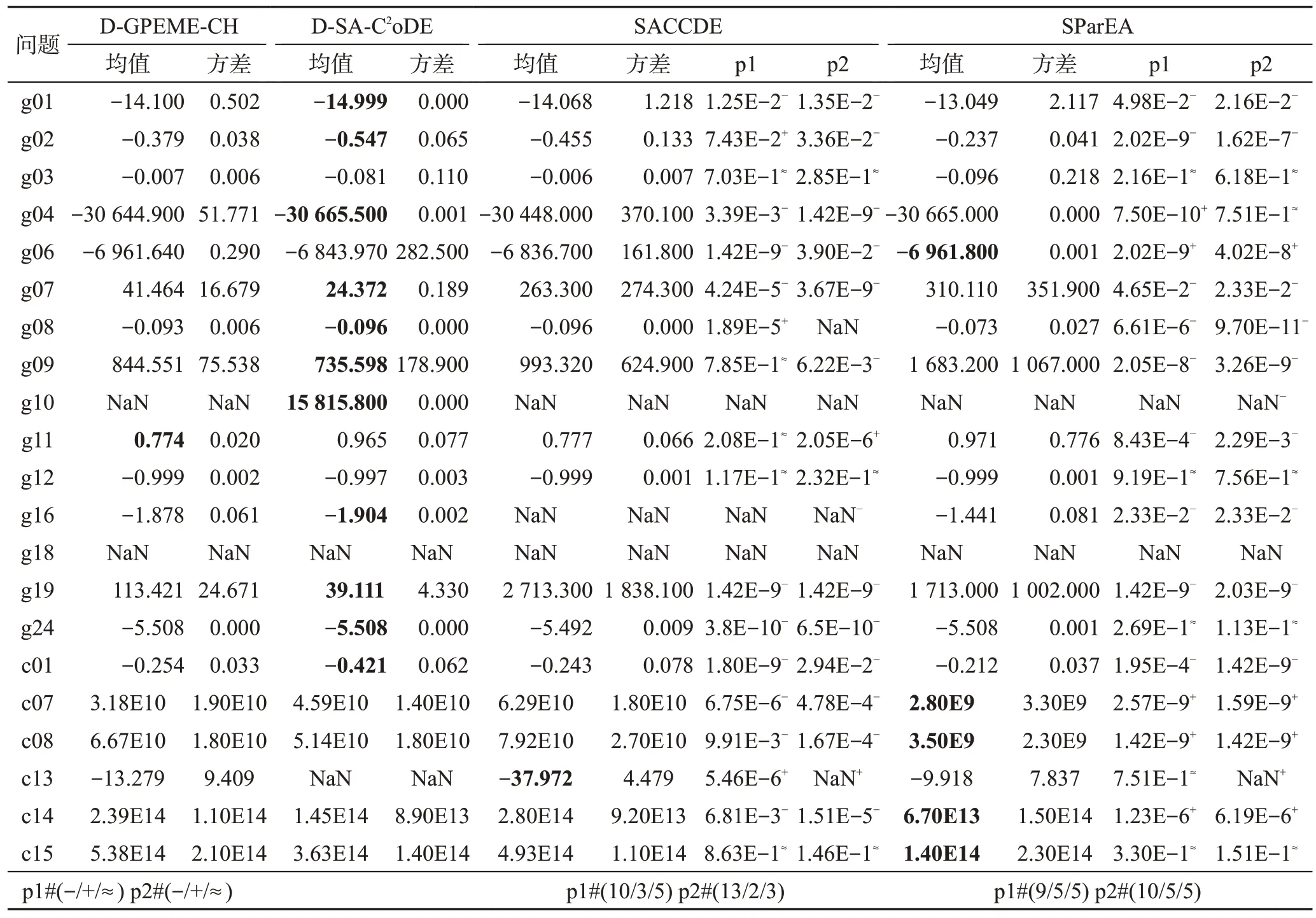
表6 自適應約束評估的SAEAs與其他SAEAs的性能對比Table 6 Comparison results of adaptive constraint evaluation aided SAEAs with other SOTA SAEAs

表6 中，p1 表示對比算法與D-GPEME-CH 的威爾克遜秩和檢驗結果，p2 表示對比算法與D-SAC2oDE的威爾克遜秩和檢驗結果。-/+/≈分別表示在顯著水平為0.05的情況下，對比算法明顯劣于、優于本文設計的算法，或與本文設計的算法無明顯差別；最后一行總結對比算法與本文設計的兩種算法總體比較情況。從表中結果可以得出以下結論：（1）SACCDE在10個測試函數中顯著劣于D-GPEME-CH，在13個函數中顯著劣于D-SA-C2oDE。（2）SParEA 在9 個測試函數中顯著劣于D-GPEME-CH，在10 個函數中顯著劣于D-SA-C2oDE。（3）SACCDE 在CEC2010 的30維函數中大部分劣于D-GPEME-CH和D-SA-C2oDE；而SParEA 在CEC2010 的30 維函數中大部分優于DGPEME-CH和D-SA-C2oDE。

上述結論是合理的。SACCDE 和SParEA 對所挑選的解進行全部約束評估。在測試集2006 中，當約束個數較多時，頻繁地評估可行域信息較多的約束對昂貴評估次數造成浪費，限制了算法的演化程度；而D-GPEME-CH 和D-SA-C2oDE 采取了自適應約束評估策略，僅對可行域信息較少的約束進行評估，能夠有效避免昂貴約束評估的浪費，使算法進一步演化。而CEC2010測試集函數設計的初衷在于問題維度的可擴展性，問題約束通常只有1個（c01,c07,c08）和3個（c13,c14,15），且約束的可行域較小，自適應約束評估策略極大概率將所有的約束加入待評估集合，因此，D-GPEME-CH、D-SA-C2oDE和SACCDE、SParEA一致，對所挑選的解進行了全部約束評估，并沒有發揮自適應約束評估策略的優勢。另外，SParEA使用了四種不同的代理模型對約束進行擬合，準確率相對于只采用一種模型的其他三種算法有所提升，因此在CEC2010測試問題中的性能表現較好。

4.4.4 運行時間對比與分析

為進一步說明SAEAs能夠提高求解昂貴優化問題的效率，本小節對自適應約束評估SAEAs 和傳統約束優化EAs 的運行時間進行統計分析。由于昂貴工程問題使用的仿真軟件需要花費幾個小時甚至幾十個小時進行一次評估，且大部分都是商用軟件，本文通過對測試函數添加時間延遲來模擬昂貴評估。不失一般性，本文采取4個函數g01、g02、g03、g04，設置一次適應值評估的時間延遲為0 s、1 s、10 s和100 s，記錄算法平均運行一次所需時間，時間延遲為0 s，即算法真實運行時間。為保證實驗的公平性和有效性，D-GPEME-CH 和D-SA-C2oDE 的停止條件如4.2節所設，為1 000×(NC+1)次，而C2oDE的停止條件為搜索結果達到兩種算法的平均值，即算法性能達到和自適應約束SAEAs相近，此時進行的評估次數分別是126 500×(9+1)(g01)、108 050×(2+1)(g02)、135 950×(1+1)(g03)、137 300×(6+1)(g04)，顯然，消耗的評估次數均遠遠大于1 000×(NC+1)。運行時間記錄如表7所示。

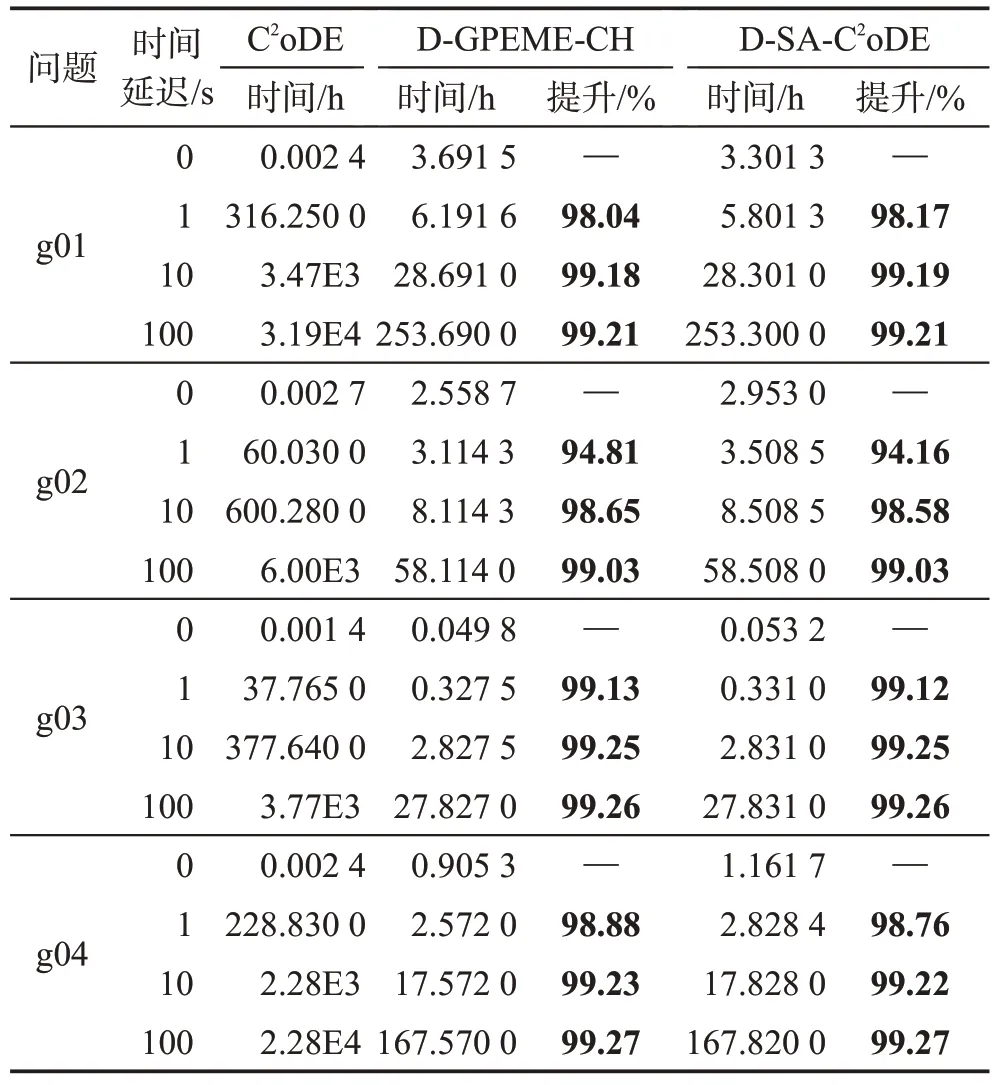
表7 不同時間延遲的運行時間對比結果Table 7 Comparison results of execution time with different time delays

表7 中效率提升的計算是由C2oDE 運行時間減自適應約束評估SAEAs 時間的差，除以C2oDE 運行時間所得。當時間延遲為0 s 時，可以看到自適應約束評估SAEAs 比C2oDE 運行時間長，這是因為模型訓練時間相對簡單函數評估較長，且維度越高，問題越復雜，訓練時間越長；而真實函數評估所需時間非常短，因此在運行時間對比上并沒有優勢。然而，當單次適應值評估有時間延遲后，自適應約束評估SAEAs 運行時長比C2oDE 效率提升在94%以上，其中91.67%的測試例子效率提升在98%以上。這是因為模型的訓練和預測時間相對昂貴函數評估較短，在代理模型的輔助下，真實適應值評估次數大大減少，由此減少了評估時間，加快算法運行效率。隨著時間延遲的增大，自適應約束評估SAEAs 的時間優勢更加明顯，效率提升幅度更大。

4.4.5 工業問題優化結果與分析

為進一步證明自適應約束評估SAEAs在工業中有良好的應用前景，本小節在碟形彈簧設計優化（BS）、散貨船設計優化（BCD）、轎車側面碰撞優化（CSI）和螺旋彈簧設計優化（HS）問題中將設計的兩種算法與傳統約束優化方法C2oDE 進行對比實驗，并進行威爾克遜秩和檢驗，實驗結果如表8所示。

表8 工業優化問題的實驗對比結果Table 8 Comparison results in engineering optimization problems

由表8 中結果可得，D-GPEME-CH 和D-SAC2oDE均取得比C2oDE好的結果。特別地，顯著水平為0.05 時，D-GPEME-CH 在兩個問題中顯著好于C2oDE，D-SA-C2oDE在四個問題中均顯著好于C2oDE。因此，本文設計的兩種自適應約束評估SAEAs 能夠對四個工業約束優化問題進行有效求解，在自適應約束評估策略的輔助下，能夠提升對可行域搜索的成功率，表現出其在昂貴復雜工業約束優化問題中較好的應用前景。

4.5 理論分析

首先在性能方面，算法的性能受演化程度影響，自適應約束評估策略從演化程度提升算法性能。現有的處理昂貴約束方法大都是對每個候選解進行全部約束和目標評估，即每一代消耗NC+1 次昂貴評估，對應的演化程度為maxFES/(NC+1)。而在自適應約束評估策略中，算法根據當前種群對可行域信息的掌握程度自適應決定評估約束。具體地，本文將約束分為三大類：第一類是初始化隨機采樣種群在可行域內比例達到評估閾值thr，算法很容易找到可行解，在自適應約束評估策略中不會被選擇做昂貴評估；第二類是初始化隨機采樣種群在可行域內比例小于評估閾值thr，且算法非常難找到可行解，在自適應約束評估策略中被頻繁選擇做昂貴評估；第三類是初始化隨機采樣種群在可行域內比例小于評估閾值thr，但隨著演化種群在可行域內比例會達到評估閾值thr，即演化前期被頻繁選擇做昂貴評估，演化后期不會被選擇做昂貴評估。當問題的約束都是第一類時，部分評估過程中沒有約束被選擇進行昂貴評估；全部評估過程對所有約束和目標值進行昂貴評估，因此演化程度為[maxFES/(NC+1)]×(Gap+1)，其中，如第2 章描述，Gap是需進行信息補全的代數，它決定著算法進行種群和代理模型更新的頻率，因此Gap≥1。此時，算法演化程度滿足以下關系：

這時，自適應約束評估策略的演化代數與所有約束評估策略的演化代數成倍數關系，Gap越大，演化代數越多，演化程度越高。當問題的約束都是第二類時，部分評估過程中所有約束被選擇進行昂貴評估；全部評估過程僅對目標值進行昂貴評估，因此演化程度為[maxFES/(NC×Gap)]×(Gap+1)。結合Gap≥1，算法演化程度滿足以下關系：

因此，在所有約束被選擇進行昂貴評估的情況下，自適應約束評估策略的SAEAs的演化程度都比對所有約束進行昂貴評估的SAEAs 高。也就是說，自適應約束評估策略在最差情況下每一代消耗的昂貴評估次數也比所有約束進行昂貴評估的方法少，演化程度高。當問題的約束為第三類時，或者包含這三類中的多類約束時，演化程度在區間{[maxFES/(NC×Gap)]×(Gap+1)，[maxFES/(NC+1)]×(Gap+1)}內，因此，在求解包含不同類型約束的問題時，自適應約束評估策略能夠在少量評估次數下自適應評估昂貴約束，提升算法性能。

其次在運行時間方面，由4.4.4小節知，C2oDE取得和D-GPEME-CH、D-SA-C2oDE 在1 000×(NC+1)次評估相近的效果需100倍以上評估次數，為方便說明，記C2oDE 評估次數為1 000×times×(NC+1)，其中，times是達到相近效果所用評估倍數。由于CEC2006 函數并非昂貴優化問題，在時間延遲為0 s時，模型的訓練和預測時間占支配地位，因此C2oDE運行時長較短。當對真實評估加上時間延遲td模擬昂貴約束優化時，評估時間占支配地位。此時，DGPEME-CH、D-SA-C2oDE所需的評估時間為1 000×(NC+1)×td，而C2oDE所需的評估時間為1 000×times×(NC+1)×td，效率提升如下：

由此可知，基于代理模型的算法的效率提升與傳統算法所需評估次數有關，所需評估次數越多，效率提升越大。由表7可知，本文算法的效率提升均在94%以上，且大部分達到98%。

4.6 算法對比分析

本文從兩個思路出發設計兩種基于自適應約束評估策略的約束優化SAEAs，D-GPEME-CH 和DSA-C2oDE，二者具有一定的相似性。首先，二者都采用高斯過程回歸模型作為代理，在昂貴約束和目標的擬合上沒有本質區別；其次，二者都采用自適應約束評估策略對昂貴約束進行處理，在演化過程中都能夠自適應決定評估的約束，節省的評估次數用來進一步演化，相對于傳統約束優化算法能夠在有限次真實評估下找到優勝解。

然而，這兩個算法在演化算子上也存在一定的差異性。D-GPEME-CH是基于代理模型輔助的無約束演化算法加入約束處理技術設計的，本身的演化算子為DE/best/1，無需處理約束；而D-SA-C2oDE 是由無代理模型的約束優化算法加入代理模型的輔助設計的，采用的是復合差分進化算法，并設計有良好的約束處理技術。因此，D-GPEME-CH 在對可行域的搜索和收斂能力上較D-SA-C2oDE 差，算法性能不如后者，這也體現在CEC2006 及工業優化問題的測試結果中。相對應地，D-SA-C2oDE 的演化算子較為復雜，導致D-SA-C2oDE 的運行時間普遍較DGPEME-CH 長，這體現在運行時間對比與分析的實驗中。但是，即使二者在性能和時間上有所差異，在真實評估次數非常有限的情況下，它們都比傳統無代理模型輔助的約束優化算法有更好的搜索能力和更高效的求解時長。事實上，無論從哪個思路出發設計約束優化SAEAs都有挑戰。

（1）從基于代理模型輔助的無約束優化算法思路出發，由于昂貴約束的加入，需要考慮如何合理處理約束。昂貴約束與昂貴目標性質不同，約束不需尋找最優值，只要在可行域內的解都是滿足的；另外，在多目標或超多目標的優化問題中，目標的個數往往小于5，而約束個數大于10的優化問題是非常多的，這使得可行域空間變得極其復雜，在利用代理模型擬合約束時要考慮如何對復雜約束進行有效處理。

（2）從無代理模型輔助的約束優化算法思路出發，代理模型的加入需要考慮如何選擇代理模型，如何使用代理模型以及如何對模型進行有效管理。代理模型的預測結果相比真實評估有一定的誤差，如何降低預測誤差的負面影響，是這類問題的研究重點。同時，當約束個數增加時，如何降低模型管理負荷，提高算法運行效率也需進行考慮。

因此，當前約束優化SAEAs 的設計仍然存在很多挑戰，對于昂貴約束優化問題的求解仍有較大的研究空間。

5 總結與展望

本文提出了一種新的自適應約束評估策略來自適應地進行個體選擇、約束選擇和昂貴評估。為驗證該策略在約束優化SAEAs 中的作用，本文分別從代理模型輔助的無約束優化算法和無代理模型的傳統約束優化算法兩個思路出發，設計兩種自適應約束評估SAEAs：D-GPEME-CH和D-SA-C2oDE。通過在測試集CEC2006和四個工業優化問題中的實驗驗證及理論分析，表明本文設計的自適應約束評估SAEAs 能夠在較短時間內有效求得可行解，降低求解昂貴約束優化問題的時間成本，在復雜的昂貴工業約束優化問題中有較好的應用前景。

在今后的研究中，可以就如何利用局部模型對已有信息進一步開發，加快算法對可行域的探索，提高算法求解質量展開進一步研究。