注重研“形”求“理”，達成解題高效

摘? 要：以2021年中考北京卷第27題為例，通過多角度、多方位的剖析，基于多解追求“最佳”；立足多解與系統(tǒng)觀的有機結(jié)合；注重研“形”求“理”，交融共進，高效達成解題，體現(xiàn)試題的育人價值.

關(guān)鍵詞：試題評價；基本圖形；解題教學；教學啟示

基于中考試題開展解題研究和教學實踐是數(shù)學教師的基本教學任務(wù)，也是提高學生解題能力的基本途徑. 教師對中考試題的解讀不到位、不深刻，會導致解題教學中的“滑過”現(xiàn)象，學生只能獲得問題的答案，而失去了獲得解法背后的數(shù)學原理和對數(shù)學問題本質(zhì)的感悟的機會，這樣的解題教學對試題本身來說僅是管中窺豹、未知萬一. 若從試題評價角度切入，深入剖析試題，結(jié)合一題多解開展針對性的解題教學，則能有效提高中考試題的教學價值. 基于“雙減”背景，解題教學自會走向“減量增質(zhì)”，力求達到“做一題，會一類，通一片”的教學效果. 筆者以2021年中考北京卷第27題為例，拋磚引玉，淺談對解題教學的理解與思考.

一、試題呈現(xiàn)

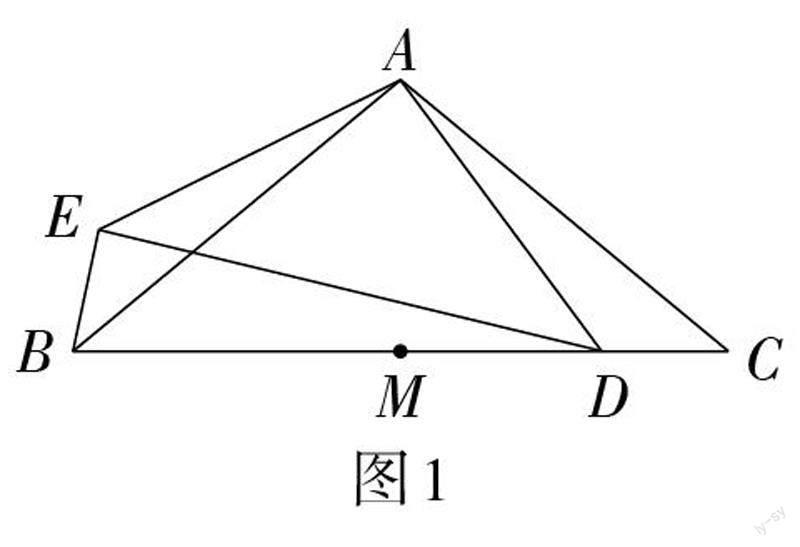
題目? 如圖1，在△ABC中，AB = AC，∠BAC = α，M為BC的中點，點D在MC上，以點A為中心，將線段AD順時針旋轉(zhuǎn)[α]得到線段AE，連接BE，DE.

（1）比較∠BAE與∠CAD的大小；用等式表示線段BE，BM，MD之間的數(shù)量關(guān)系，并證明.

（2）過點M作AB的垂線，交DE于點N，用等式表示線段NE與ND的數(shù)量關(guān)系，并證明.

二、試題評價

1. 常規(guī)出新意，“手拉手”模型巧拓展

此題中蘊含的“手拉手”模型，師生都比較熟悉，但此題把“手拉手”模型與線段中點的論證結(jié)合在一起，設(shè)計非常巧妙. 特別是第（1）小題證明過程中涉及的結(jié)論和全等三角形的性質(zhì)緊密關(guān)聯(lián)，并隱含第（2）小題的多種論證思路，如BA平分∠EBC，∠EDB = ∠EAB = ∠CAD等，為第（2）小題的論證作好了鋪墊，可謂謀篇布局，寓意深遠. 第（2）小題把三角形的中位線定理、等腰三角形的性質(zhì)、全等三角形的判定等多種初中階段重要的數(shù)學知識進行巧妙融合，考查指向基本圖形的分離與重構(gòu)，以及學生的推理能力和運算能力. 同時，檢驗了學生論證思維構(gòu)建與解題路徑設(shè)計的深層次能力.

2. 分解聯(lián)重構(gòu)，線段中點拓展思維

幾何問題的解決，重在對基本圖形的分解與重構(gòu).此題具有北京卷中考試題一貫提倡的多路徑考查學生拓展思維的鮮明特色，問題看似普通，實則意蘊深遠. 線段中點的證明思路頗多，如構(gòu)造中位線，巧用等腰三角形“三線合一”的性質(zhì)、全等三角形對應(yīng)邊相等等基本路徑. 究其本質(zhì)，無論采用哪種路徑，都需要對基本圖形進行分解與重構(gòu)，即添加合適的輔助線還原基本圖形. 從后文提及的幾種解法來看，構(gòu)造輔助線的方法非常巧妙，實則也是通性通法，歸根結(jié)底是對基本圖形的思考和應(yīng)用. 這也體現(xiàn)了試題設(shè)計的初衷，即基于對解題思路構(gòu)建、嘗試、驗證和反思的過程，考查學生的思維能力和數(shù)學核心素養(yǎng).

3. 直觀促想象，解題過程凸顯素養(yǎng)

幾何教學應(yīng)該幫助學生建立分離基本圖形的能力，使學生感知、運用基本圖形進行思考，借助幾何直觀和空間想象構(gòu)建幾何問題的數(shù)學模型，對問題進行探索，并促進邏輯推理的鍛煉與養(yǎng)成. 此題立足旋轉(zhuǎn)變換，聚焦線段中點的拓展應(yīng)用，通過空間想象達成對學生幾何直觀素養(yǎng)的培養(yǎng)；立足多種路徑解題促進學生邏輯思維多角度、全方位地深度思考與養(yǎng)成. 問題由易到難，思維水平呈進階式上升，讓不同水平的學生立足自身素養(yǎng)基礎(chǔ)，達成對應(yīng)路徑的思考與設(shè)計，使解題過程成為學生展示素養(yǎng)的舞臺.

三、解法賞析

第（1）小題相對簡單，主要是為了引導學生經(jīng)歷思維過程，為第（2）小題的論證作好鋪墊.

第（1）小題證明：由線段AD順時針旋轉(zhuǎn)α得到線段AE，可得AE = AD，∠EAD = ∠BAC = α. 所以∠EAB = α - ∠BAD = ∠CAD. 因為AB = AC，所以△EAB ≌ △DAC. 所以BE = DC. 因為M是BC的中點，所以BM = MC = DM + DC = DM + BE.

順著第（1）小題的結(jié)論，根據(jù)旋轉(zhuǎn)的性質(zhì)，容易確定△AED是等腰三角形. 實際上，參照“手拉手”模型，在△EAB ≌ △DAC的結(jié)論下，可知證明全等的目的是進一步得出相關(guān)的角和邊之間的等量關(guān)系，于是有∠EBA = ∠C = ∠ABC，即BA是∠EBC的平分線. 另外，還可以得到∠EDA = ∠C和∠BDE = ∠BAE = ∠DAC. 這些重要結(jié)論作為基礎(chǔ)條件，對第（2）小題的證明起到了至關(guān)重要的作用.

第（2）小題結(jié)論的判斷與證明過程中的思維量較大，具有較好的教學價值，接下來我們將進行重點分析.

在明確NE與ND的數(shù)量關(guān)系時，學生需要先進行猜想，容易得出NE = ND. 接下來是證明結(jié)論，考查學生對線段中點證明路徑的思考與選擇.

思路1：構(gòu)造三角形的中位線.

如圖2，延長MH，與BE的延長線交于點G. 分離圖形，可以直觀看出點N為△BED的邊DE的中點，可以通過三角形的中位線來證明，即過點N作NF∥BE交BD于點F，此時，只需要證明點F是BD的中點即可.

要證得點N為DE的中點，NF必是△BED的中位線，也就是點F是BD的中點，即BF = DF. 考慮到已有BM = MC，BE = DC，所以FM =1/2BE. 事實上，學生在思考時，還是會遇到思維的瓶頸，即如何聯(lián)系FM和BE. 很多學生想到借助BA是∠EBD的平分線，于是延長MH，與BE的延長線交于點G. 此時，根據(jù)等腰三角形“三線合一”的性質(zhì)可以進一步證得∠BMG = ∠G. 又由NF∥BE，得到∠G = ∠FNM，所以∠BMG = ∠FNM，使得FM = FN. 再根據(jù)NF =1/2BE，得到FM =1/2BE. 由點F為BD的中點，得到FN是△BDE的中位線，并“解決”問題. 這里出現(xiàn)了把“NF =1/2BE”作為已知條件來使用的情況，這在事實上已經(jīng)認定NF為△BED的中位線，顯然是錯誤的. 也有個別學生嘗試通過先定BD中點為F，再證NF∥BE，試圖證明NF為△BED的中位線，顯然也是無法實現(xiàn)的.

那么，是不是通過中位線無法證明結(jié)論呢？以上構(gòu)造中位線是通過“先定三角形，再構(gòu)造中位線”，能否換個角度，先定中位線，再構(gòu)造三角形呢？具體證法如下.

證法1：如圖3，過點E作EP∥HM，交BC于點P，

則有EP ⊥ AB.

由已知可得BA平分∠EBD，所以BE = BP.

所以DC = BE = BP.

因為BM = MC，所以PM = MD.

所以MN是△PED的中位線，

故EN = DN.

【評析】構(gòu)造中位線是證明線段中點的常見思路，關(guān)鍵在于構(gòu)造合理的三角形和對應(yīng)中位線. 三角形的中位線既能證明兩直線平行，又能證明線段相等. 因此，常見的構(gòu)造方案：一是定三角形，構(gòu)造中位線；二是定中位線，構(gòu)造三角形.

思路2：構(gòu)造等腰三角形.

從證明點N為三角形一邊的中點出發(fā)，通過等腰三角形“三線合一”求證也是一種常規(guī)路徑. 證明EN = DN，可以借助等腰三角形EAD來實現(xiàn)，即連接AN，證明AN是△EAD的邊DE上的高線或是∠EAD的平分線.

證法2：如圖4，連接AN，AM，易得AM ⊥ BC.

則∠AMC = 90°.

因為AM平分∠BAC，所以∠HAM = ∠MAC.

因為MH ⊥ AB，所以∠AHM = ∠AMC = 90°.

所以∠AMH = ∠C.

因為∠C = ∠ADE，所以∠AMH = ∠ADE.

所以A，N，M，D四點共圓.

所以∠MAN = ∠MDN，∠AND = ∠AMD = 90°，

即AN是△AED的邊DE上的高線.

因為△AED為等腰三角形，

所以AN是△AED的中線.

所以EN = ND.

證法3：如圖4，由證法2可知A，N，M，D四點共圓.

所以∠MAN = ∠MDN = ∠BAE = ∠CAD.

所以∠EAN = ∠BAE + ∠NAH = ∠MAN + ∠NAH = ∠BAM = ∠CAM = ∠DAM + ∠CAD = ∠DAM + ∠MAN = ∠DAN，

即AN平分∠EAD.

所以EN = ND.

【評析】“三線合一”是等腰三角形的重要性質(zhì)，也是等腰三角形與“中點”相關(guān)問題的解題基本思路. 在等腰三角形的條件下，利用中線、高線和角平分線“知一得二”，構(gòu)建高線或角平分線證明中線是問題解決的常見思路.

思路3：構(gòu)造全等三角形.

證明EN = ND，也可以通過全等三角形對應(yīng)邊相等來證.

證法4：如圖5，延長MH，交BE的延長線于點G，過點D作DF∥BE交HM的延長線于點F.

由BA平分∠EBC，MH⊥AB，

得∠G = ∠BMG，BG = BM.

因為CD = BE，所以EG = DM.

因為DF∥BE，所以∠F = ∠G = ∠BMG = ∠DMF.

所以DF = DM = EG.

因為∠ENG = ∠DNF，所以△ENG ≌ △DNF.

所以EN = ND.

在構(gòu)造全等三角形的解題路徑下，難以找到構(gòu)造圖形的思路時，常見的方法是構(gòu)造全等的直角三角形.

證法5：如圖6，分別過點D，E作直線HM的垂線，垂足分別為點F，K，延長BE，與NH的延長線交于點G.

參考證法4的結(jié)論，易證Rt△EKG ≌ Rt△DFM.

所以EK = DF.

因為∠ENK = ∠DNF，∠EKN = ∠DFN = 90°，

所以△EKN ≌ △DFN.

所以EN = ND.

【評析】利用全等三角形對應(yīng)邊相等實現(xiàn)線段相等（包括線段中點）的證明，是一種常見的證明思路. 解決問題的關(guān)鍵在于利用已有的兩條線段，結(jié)合已知條件，合理構(gòu)造全等三角形.

四、教學啟示

1. 基于多解追求“最佳”是解題教學的基本要求

對于解題教學，教師常常疑惑要開展一題多解還是只教“最佳”解法. 一些教師認為，沒必要一題多解，因為多解中必有“最佳”，只教“最佳”，簡潔明了，直奔主題，省時省力；一些教師認為，一題多解能有效培養(yǎng)學生的解題能力，解題時可以有多種方法供學生選擇，有備無患. 基于上述對2021年中考北京卷第27題解答過程的研討，筆者認為，立足一題多解，幫助學生尋求基于自身的“最佳”解法，是解題教學的基本要求. 常說的“做百題不如深研一題”是非常有道理的. 例如，第（2）小題對于3種類型5種證法的研究，通過一題多解能有效觸發(fā)學生多角度、多方位的思考，全面聯(lián)動數(shù)學知識，促進數(shù)學知識體系的有效構(gòu)建，落實能力與素養(yǎng)的培養(yǎng). 教學中，基于對以上5種證法的對比與分析，在尋求“最佳”方法的過程中，能有效培養(yǎng)學生的辯證思維，達成深度學習，有效構(gòu)建數(shù)學知識與能力體系.

2. 立足多解與系統(tǒng)觀的有機結(jié)合是解題教學的關(guān)鍵追求

解題教學中，面對復雜的問題時，我們常常發(fā)現(xiàn)教師分析得頭頭是道，學生則聽得一頭霧水、唉聲嘆氣. 教師的解題能力很強，教出來的學生解題能力卻很弱，是不是我們的教學出了問題？例如，此題第（2）小題的求證，需要學生具備很強的圖形重構(gòu)能力，以及幾何直觀和空間想象素養(yǎng)，快速解題并不容易. 如果學生已經(jīng)系統(tǒng)掌握了線段中點的基本證法，那解決問題自然也會水到渠成.

造成學生解題障礙的原因出在哪里？筆者認為，教師未重視多解路徑建設(shè)與系統(tǒng)觀的有機結(jié)合是造成學生解題障礙的一個重要因素. 那么解題教學中要如何做好多解路徑建設(shè)與系統(tǒng)觀的有機結(jié)合？首先，要做多解嘗試，即從不同角度進行思考與解答問題，如此題第（2）小題的5種證法；其次，在解題后要引導學生進行辨析與歸類，如將5種證法歸納為3類；最后，將基于線段中點的證法納入知識和思維系統(tǒng)，與其他知識形成整體構(gòu)建，建立基于幾何直觀與空間想象的思維體系，使得以后遇到類似問題時能夠快速獲得對解題路徑的聯(lián)想，自然產(chǎn)生對基本圖形的辨析、分離和重構(gòu)，從一題多解到多解歸一，使解題經(jīng)驗升華到系統(tǒng)思維高度.

3. 注重研“形”求“理”、交融共進是解題教學的核心價值

基本圖形在數(shù)學解題中有著舉足輕重的作用. 但是，到底是側(cè)重于基本圖形的“形”的記憶、辨認與運用，還是注重“形”背后的數(shù)學原理和深層次的邏輯理解形成“理”的探索更重要？這個問題一直困擾著教師與學生. 筆者認為，幾何解題教學既要立足基本圖形，又要注重對數(shù)學原理的理解和邏輯建構(gòu)，兩者相互融合、缺一不可. 學生的解題能力要通過學習過程的體驗，在知識、能力、思維上逐漸達成進步. 通過研究“形”去追求“理”是數(shù)學解題教學的本質(zhì)追求. 因此，在教學中，我們既要培養(yǎng)學生注重對基本圖形的“形”的提煉、辨認、分離、聯(lián)想和重構(gòu)，也要注重培養(yǎng)學生對基本圖形的“理”的探索、理解、詮釋、感悟和內(nèi)化，這樣才能使學生的解題能力得到實質(zhì)性的提升.

參考文獻：

［1］鄭振興. 研讀試題? 分步遞增? 跳出題海? 提升素養(yǎng)：以2018年浙江省溫州市數(shù)學中考第15題為例［J］. 中學教研（數(shù)學），2019（4）：21-23.

［2］段志貴. 構(gòu)造：讓解題突破思維瓶頸［J］. 數(shù)學通報，2018，57（9）：53-57.

［3］鄭振興. 探索解題路徑? 發(fā)展關(guān)鍵能力［J］. 中學數(shù)學教學參考（中旬），2021（9）：57-59.

［4］蔡衛(wèi)兵. 思維在多解中提升? 素養(yǎng)在探究中發(fā)展：一道中考試題的教學運用［J］. 中國數(shù)學教育（初中版），2021（5）：44-49.

［5］劉志昂. 立足基本圖形? 追尋多題歸一：從一道教材習題及其變式說開去［J］. 中國數(shù)學教育（初中版），2018（6）：59-62.