基于神經網絡優化算法的降水量預測研究
李建磊,付世豪,宋金繁
(華北水利水電大學,鄭州 450046)
0 引言
降水量預測是對未來某地區降水做出科學的判斷或預見,根據當地的自然氣候,如氣溫、氣壓、濕度等,應用科學方法,對降水的可能性或降水量做出客觀描述,是令管理部門提前做出決策、編制計劃及進行有效處理的重要依據。
近些年,神經網絡預測方法備受關注。反向傳播(Back Propagation,BP)神經網絡算法具有任意復雜的模式分類能力和卓越的多維函數映射能力。BP算法的實質是采用梯度下降法來計算網絡誤差函數的最小值。但若目標函數很復雜,則會出現鋸齒形現象,導致BP算法收斂速度慢。BP算法是一種局部搜索最優解的優化方法,有可能會使算法陷入局部最優解,也會發生過擬合現象,即預測能力達到一定程度再進行訓練,隨著訓練能力的提高,預測能力反而下降。遺傳算法(Genetic Algorithm,GA)是一種進化算法,具有良好的容錯性和一定程度的自適應自組織能力,使用概率機制進行迭代,具有一定的隨機性,還擁有良好的學習識別功能等,所以遺傳算法作為一種具有高度并行、隨機、自適應的搜索算法,是一種全局搜索最優解的方法,可擴展性強,易與BP算法結合,故使用遺傳算法優化的BP算法可解決學習速度慢、易陷入局部最優等問題。
1 BP神經網絡預測模型
BP神經網絡有兩個步驟,即信號的正向傳播和誤差的反向傳播,并在誤差反向傳播過程中不斷優化權值于閾值,得到最優參數,保存網絡。BP算法的實質是采用梯度下降法沿著誤差函數的負梯度方向修改權值和閾值,從而獲得最合適的結果[1]。以下是建立BP網絡模型的步驟:
1)設置模型輸入輸出樣本、創建網絡。

3)輸入訓練樣本與預測樣本,對數據進行預處理。輸入樣本:X=(x1,x2,…,xn)T,期望輸出:d=(d1,d2,…,dn)T。對數據使用MATLAB自帶的mapminmax函數進行歸一化處理。Mapminmax的數學公式:
(1)
其中,xmin、xmax分別為映射前的矩陣每一行的最小值和最大值;ymin、ymax分別為映射到的新矩陣每一行的最小值和最大值。
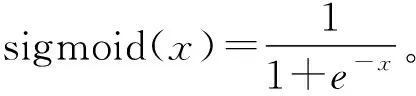

6)計算網絡誤差。當網絡誤差達到預設值或學習次數大于設定的最大次數,則結束訓練;否則,選取下一個訓練樣本和對應的期望輸出,返回到3),進入下一輪學習。
7)網絡訓練結束后,對預測樣本進行預測并輸出預測值。
2 基于GA優化的BP神經網絡預測模型
遺傳算法的作用是優化BP神經網絡的初始權值與閾值,是一個不斷修正閾值與權值的過程,經過訓練,可使誤差越來越小[2-4]。訓練后,再對網絡進行測試。以下是基于遺傳算法優化的BP神經網絡預測模型實現:
1)輸入神經網絡初始樣本數據并對其進行預處理。
2)種群初始化。
編碼。對每個個體使用實數編碼,將其編碼為一個實數串,由輸入層與隱含層連接權值、隱含層閾值、隱含層與輸出層連接權值、輸出層閾值4個部分構成遺傳算法的染色體,每個染色體長度為:
S=m×h+h+n×h+n
(2)
其中,m、h及n分別為輸入層節點數、隱藏層節點數及輸出層節點數。
種群規模。種群規模若是過大,會造成資源浪費且難以收斂;種群規模若是過小,遺傳算子會產生隨機誤差,即模式采樣誤差,會妨礙小群體中有效模式的傳播,從而造成收斂于局部極小點。一般情況下,種群規模通常取20~200。
進化代數。進化代數不宜過大,過大會增加時間消耗,通常選取100~1 000。
3)將BP神經網絡訓練得到的誤差作為適應度值,即評價函數確定為期望值與預測值的絕對誤差函數。
(3)
其中,k是系數,d、o分別為期望輸出與預測輸出。
4)確定遺傳算法的選擇操作、交叉操作、變異操作方法的選取。評價函數、選擇操作、交叉操作及變異操作方法的選取分別為絕對誤差函數、輪盤賭法、實數交叉及隨機變異。
設定交叉概率與變異概率。
交叉概率。交叉概率過大,隨機性增加,會造成最優個體的丟失,還會導致不必要的時間浪費;交叉概率過小,不能有效更新種群,還會阻礙算法搜索。一般選為0.2~1.0。
變異概率。變異概率越大,變異操作被執行的次數越多。較好的變異概率產生的新生代摒棄父代的不良基因,能完整保存信息。若變異概率過大,則可能造成種群已有的優良模式被破壞;若變異概率過小,又會使種群的進化速度降低。通常取值為0.001~0.1。
遺傳算法參數設定:種群規模為20~200,進化代數為100~1 000,交叉概率為0.2~1.0,變異概率為0.01~0.1。
5) 對進化的數據(適應度)進行檢驗。如果達到預期目標則停止進化,如果未達到目標值且進化沒有結束,則重新計算種群的適應度,從中選出最優個體。
6) 將遺傳算法得到的最優權值與閾值賦予BP神經網絡,再進行訓練學習,達到要求后輸出預測值[5-8]。GA-BP神經網絡流程如圖1所示。
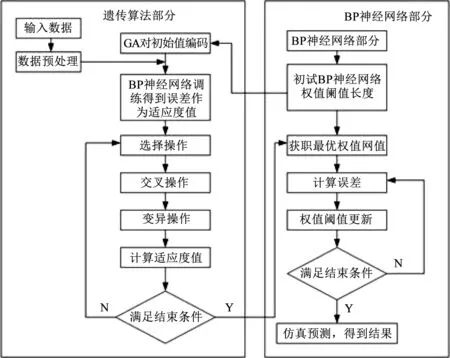
圖1 GA-BP預測模型流程圖Fig.1 Flow chart of GA-BP prediction model
3 實例分析
3.1 實驗數據
實驗數據來源于河南安陽、南陽、商丘、信陽1953年8月—2013年12月的月降水量數據。根據風速、氣壓、氣溫、氣壓、濕度等因素進行降水量預測。用于訓練的樣本是1953—2013年的降水量數據,共有725組數據,選取1953年8月—2010年12月的數據作為訓練樣本,2011年1月—2013年12月的數據為預測樣本,應用BP神經網絡和基于遺傳算法優化的BP神經網絡兩種算法對36個月的降雨量進行預測。
3.2 遺傳算法優化的BP神經網絡實驗
為了使遺傳算法達到最好的效果,進行實驗尋求遺傳算法最佳的參數設置。BP神經網絡的設置為模型參數保持不變,以3個定量、1個變量的定量分析法進行實驗。因為遺傳算法本身具有一定的隨機性,所以并不能準確地說哪個參數一定是最好的,只能找出一個大概的范圍,具體應用時可稍作調整。迭代次數選取50次進行預測實驗,實驗結果見表1。
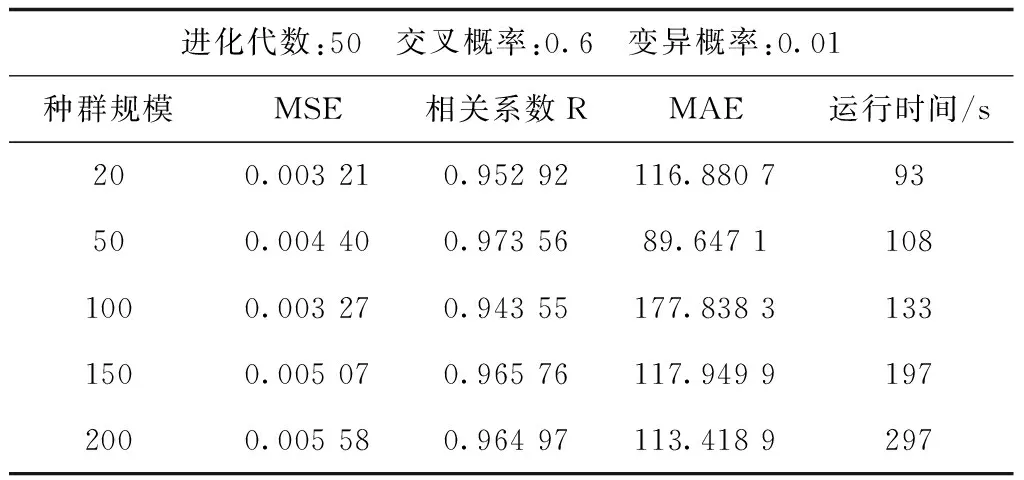
表1 各最佳種群規模實驗結果Tab.1 Experimental results of optimal population size
從結果來看,種群規模為50時,模型精度與擬合程度最高,雖然比種群規模為20、100時的最小MSE要高出0.001 2左右,但是相關系數比種群規模為20、100時的相關系數要高且平均絕對誤差要小。種群規模為100時,運行時間比種群規模為50時的運行時間要多出30 s左右。綜合來看,種群規模數選為50即可。
確定種群規模數后,需進一步確定交叉概率,實驗結果見表2。
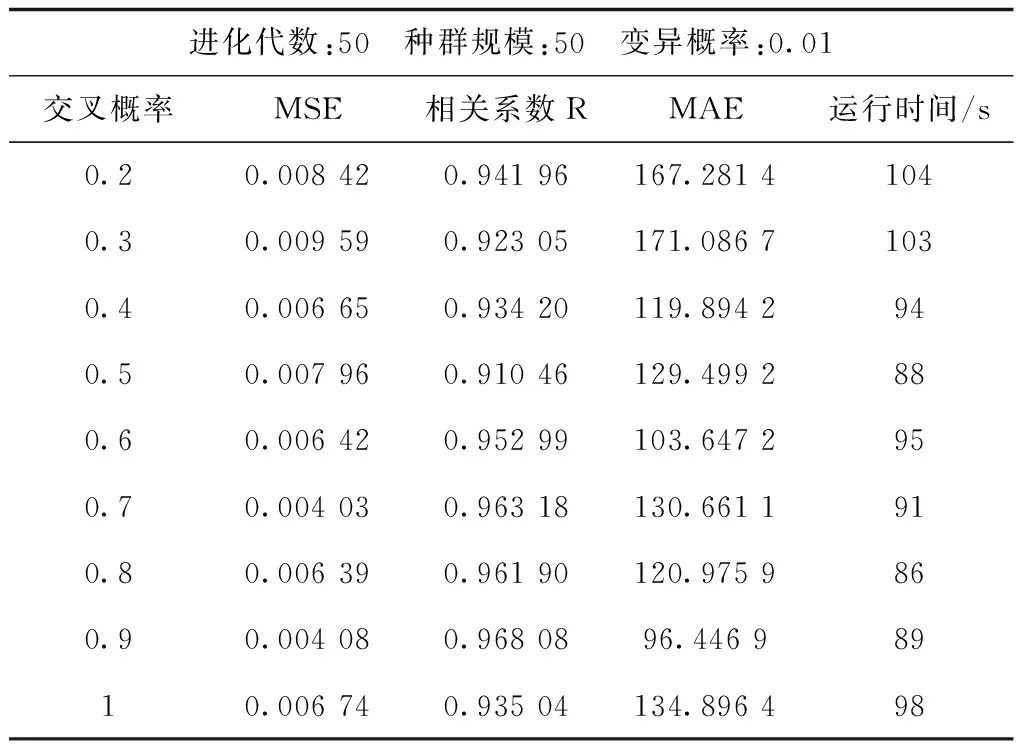
表2 各交叉概率實驗結果Tab.2 Experimental results of cross probability
算法的運行時間并沒有相差太多,觀察它們的相關系數發現,交叉概率在0.6~0.9的數據擬合度都到達了0.96左右,運行時間最高相差了11 s,但交叉概率為0.9時,最小MSE和平均絕對誤差MAE較低,以此推測交叉概率選在0.9附近即可。
為了確定變異概率,選取變異概率為0.001、0.005、0.01、0.05、0.1進行實驗,實驗結果見表3。
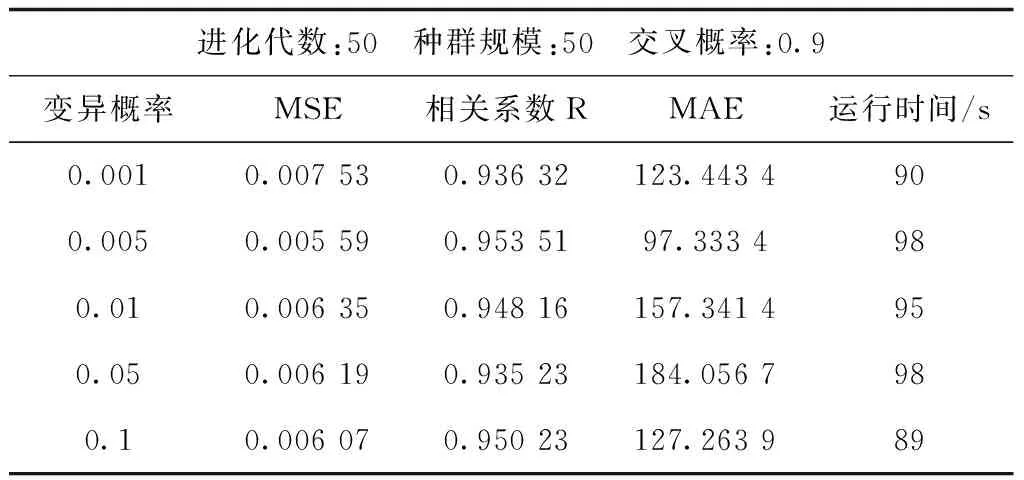
表3 各變異概率實驗結果Tab.3 Experimental results of mutation probability
從表3可以看出,變異概率為0.005與0.1時,相關系數僅差0.003 28,說明擬合能力很接近,不過雖然變異概率為0.1時的運行時間相比于變異概率為0.005時的運行時間少了9 s,但最小MSE與平均絕對誤差MAE都是變異概率為0.05時的更小,故而變異概率取0.005左右即可。
由表4可知,迭代次數為100時,相關系數最大、最小MSE與平均絕對誤差MAE最小。迭代次數為200時,雖然比迭代次數為100時的各項指標差一點,但是運行時間卻長很多。故而迭代次數選取100次即可。
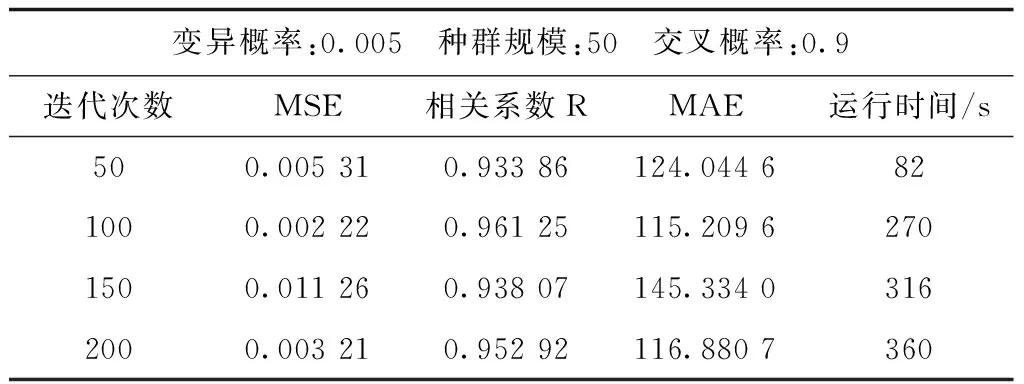
表4 各迭代次數實驗結果Tab.4 Experimental results of each iteration
4 結果分析
為了比較未優化的BP神經網絡預測模型與遺傳算法優化后的BP神經網絡預測模型在精度與擬合程度方面的差距,做出兩種模型對河南安陽、南陽、商丘、信陽4個站點采用BP神經網絡預測模型與GA-BP神經網絡預測模型進行降水量預測的預測結果與誤差對比圖,如圖2所示。
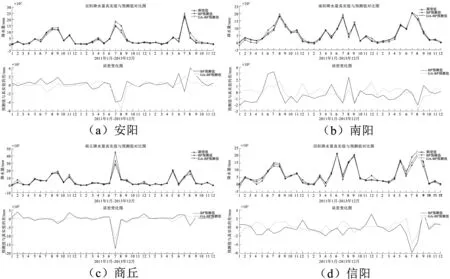
圖2 GA-BP與BP預測模型對比Fig.2 Comparison of GA-BP and BP prediction models
可以看出,經過遺傳算法優化后的BP神經網絡的預測值要更加靠近真實值,說明GA-BP神經網絡預測模型確實比未優化的BP神經網絡預測模型精度更高。從誤差對比圖中可以看出,GA-BP神經網絡模型與未優化的BP神經網絡模型相比,誤差更小一些,不過也有個別月份預測的降水量誤差值甚至比未優化的神經網絡模型還要大,所以需要進一步分析,給出各地區使用兩種預測模型進行預測后的平均絕對誤差MAE、最小MSE、均方根誤差RMSE及相關系數R,如表5所示。
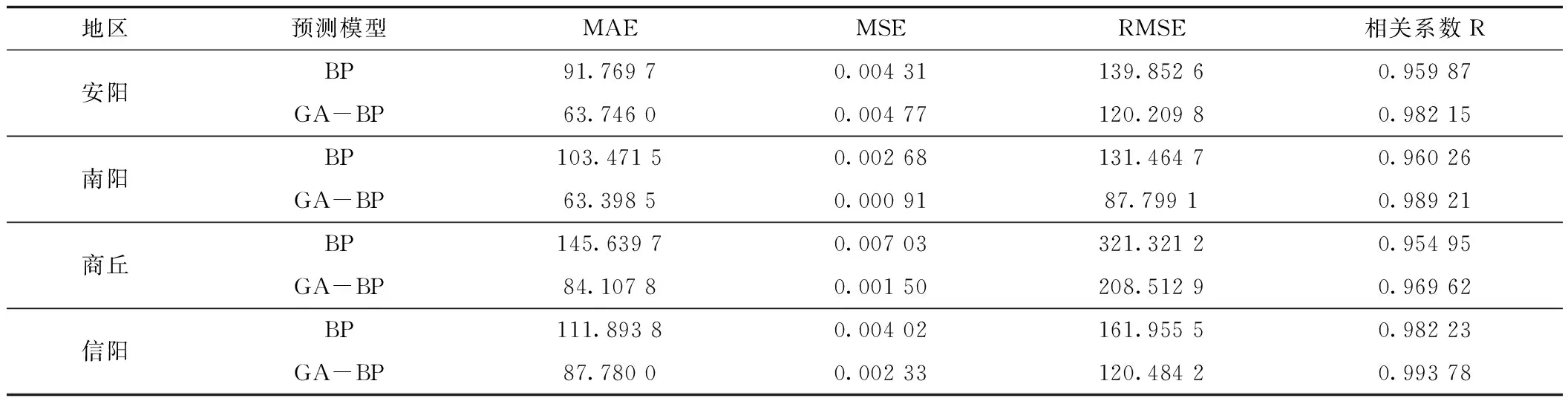
表5 GA-BP與BP預測模型誤差Tab.5 Error of GA-BP and BP prediction model
根據表5可以看出,安陽、南陽、商丘、信陽等地應用遺傳算法優化后的BP神經網絡模型預測的降水量平均絕對誤差MAE要比BP神經網絡模型平均小了38.435 6,均方根誤差RMSE平均小了54.397,相關系數平均提升了0.193 6。南陽市GA-BP模型預測的降水量最小MSE比BP模型的最小MSE小了0.001 778,這幾乎是BP模型的一半,而商丘市兩個模型的最小MSE相差了0.005 523 3,也就是說BP模型的最小MSE是GA-BP模型最小MSE的4.68倍,且商丘市GA-BP模型預測的降水量MAE、RMSE分別比BP模型小了61.531 9、112.808 3,幾乎小了一半。由此得出,GA-BP神經網絡模型相對于BP神經網絡模型,精度確實提高了不少。
5 結論
將遺傳算法算法與BP算法有機融合, 大大提高了模型預測精度,不過某些月份降水量預測誤差值卻比未優化的BP預測模型誤差更大,說明遺傳算法優化后的BP神經網絡從全局來看確實比BP神經網絡預測模型精度高,但是從局部來看,遺傳算法優化后的BP神經網絡還不是很理想[9-10]。

