基于Dandelin 雙球模型對一道高三調研試題的溯源探究

福建省南平市高級中學(353000) 江智如 陳美婷 蔡 珺

1 試題呈現

試題(2023 屆廣州高三年級調研測試B 卷第16 題)如圖1, 是數學家Germinal Dandelin用來證明一個平面截圓錐得到的截口曲線是橢圓的模型. 在圓錐內放兩個大小不同的小球,使得它們分別與圓錐的側面與截面都相切, 設圖中球O1, 球O2的半徑分別為4 和2, 球心距離,截面分別與球O1,球O2相切于點E,F(E,F是截口橢圓的焦點),則此橢圓的離心率等于____.

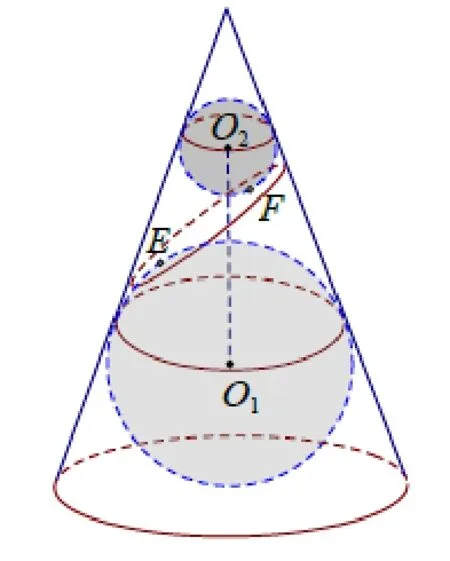
圖1

2 試題分析

本試題以Dandelin 雙球模型為載體,考查圓錐曲線內容,要求考生會根據對幾何圖形的分析,探索解決問題的思路[1].考查圓錐與球相切、截面、橢圓第一定義和離心率等相關知識, 考查考生數形結合思想、化歸與轉化思想、空間想象能力、推理論證能力和運算求解能力,突出試題的區分與選拔功能.

3 試題溯源

2019 版人教社A 版《普通高中教科書數學選擇性必修第一冊》第104 頁第三章章頭圖中(如圖2)用一個不垂直于圓錐軸的平面截圓錐,當圓錐軸與截面所成角不同時,可以得到橢圓、雙曲線、拋物線三種不同的曲線,因此把這三種線統稱為圓錐曲線[2]. 但這種聯系在后續的圓錐曲線定義中,均未再體現,而在2005 版人教社A 版《普通高中課程標準實驗教科書數學選修2-1》第42 頁“探究與發現”中,介紹數學家Germinal Dandelin 利用兩個球的切線長相等(如圖3),可以證明截口曲線是橢圓[3]. 基于這些背景知識,本文依循數學家Germinal Dandelin 的思路,在直觀素養指引下,對試題進行溯源探究與推廣.

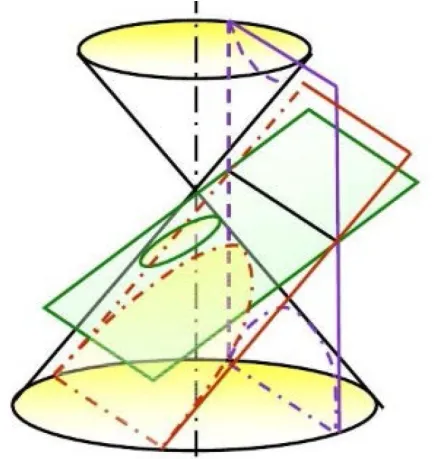
圖2

4 解法探究

引理在圓錐內放兩個大小不同的小球,使得它們分別與圓錐側面相切. 若不垂直于圓錐軸的截面分別與兩個小球相切,則截面截圓錐所得的截口曲線是以兩切點為焦點的橢圓.

證明如圖3, 在Dandelin 雙球中, 兩個小球與圓錐面的交線分別為一個圓, 并與圓錐的底面平行, 記這兩條交線圓分別S1,S2, 且所在平面分別為π1,π2, 與圓錐軸不垂直的截面π與圓錐面的截口曲線為S, 且分別與兩個小球相切于點E,F. 在截口曲線S上任取一點A,過點A的圓錐母線分別與圓S1,S2相交于點B,C, 則BC長度是兩個小球的外公切線長, 是定值, 即(其中d是球心距,r1,r2分別是兩個小球的半徑). 另一方面, 由球的切線性質可得,AE=AC,AF=AB, 于是AE+AF=AC+AB=BC>EF,即曲線S上點到兩切點的距離和為定值,所以由橢圓第一定義知,截口曲線S是以E,F為焦點的橢圓.

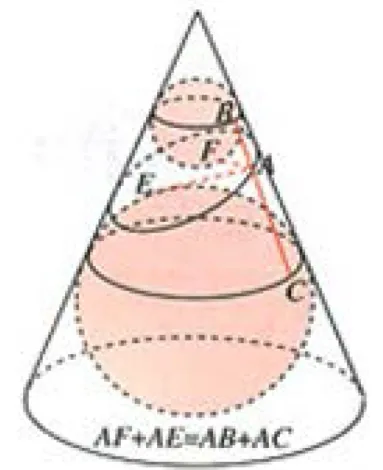
圖3

圖4

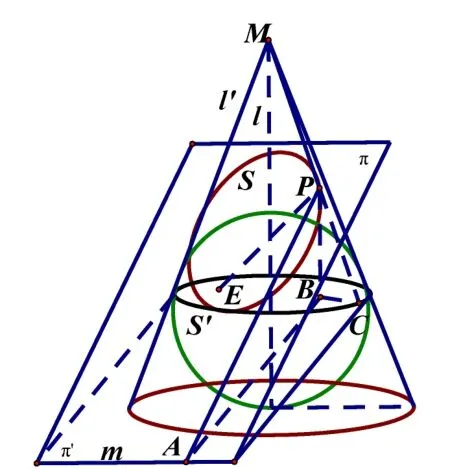
圖5

試題解析(一)依據引理的推導過程, 試題1 可以轉化為分別求橢圓的焦距2c=EF, 長軸2a=BC. 如圖4, 在圓錐的軸截面中, 連接O1O2交EF于點H, 連接O1E,O2F, 則Rt?O2FH∽Rt?O1EH, 于是, 故,從而,所以2c=EF= 3FH= 2,即c= 1. 過點O2作O2D//BC,交O1C于點D,則由圓的外公切線性質可求,,即2a=BC= 6, 所以a= 3, 因此, 橢圓的離心率為.

5 溯源推廣

6 高考應用

在歷年高考與各地的質檢中也出現Dandelin 雙球模型的試題,可以引導考生根據對問題情境的分析,運用已有數學思維方法分析問題的內部結構和內在聯系,調動相關知識與能力解決問題[5].

題目(2021 年成都七中高三二診模擬理12) 如圖6所示, 在圓錐內放入兩個球O1,O2, 它們都與圓錐相切(即與圓錐的每條母線相切),切點圓(圖中粗線所示)分別為⊙C1,⊙C2. 這兩個球都與平面α相切,切點分別為F1,F2,丹德林(G·Dandelin)利用這個模型證明了平面α與圓錐側面的交線為橢圓,F1,F2為此橢圓的兩個焦點,這兩個球也稱為Dandelin 雙球.

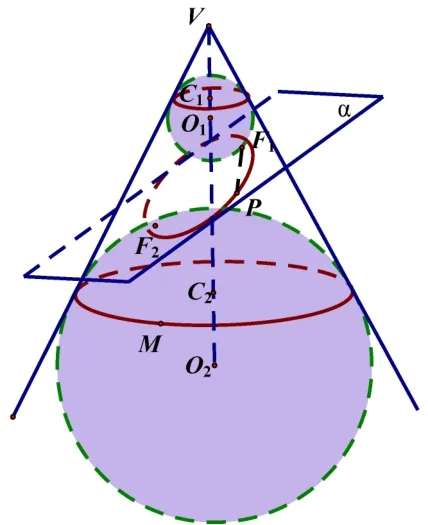
圖6

圓錐的母線與它的軸的夾角為30?,⊙C1,⊙C2的半徑分別為1,4,點M為⊙C2上的一個定點,點P為橢圓上的一個動點,則從點P沿圓錐表面到達點M的路線長與線段PF1的長之和最小值是( )

解題思路根據Dendelin 雙球模型,可以把問題轉化兩個內切球的外公切線長.

題目解析連接VP, 分別交⊙C1,⊙C2于點Q,R, 連接PF1, 則由球的切線性質可得,PF1=PQ. 設點P沿圓錐表面到達點M的路線長為dPM, 則PF1+dPM=PQ+dPM≥PQ+PR=QR,當且僅當點P是母線VM與交線橢圓的交點時取等號,而QR為兩個球O1,O2的外公切線長,故,所以最小值為3√3,因此選A.

評析本試題將圓錐、球、橢圓、動點的軌跡等內容有機結合,考查考生對Dendelin 雙球模型的理解與應用,突出考查考生運用數形結合的思想方法和綜合應用數學知識解決問題的能力,對幾何直觀能力、邏輯推理能力、運算求解能力有一定的要求,重基礎、重能力,對引領數學課程改革有導向作用.

7 結語

在高考評價體系[5]指引下, 高中幾何教學應由傳統的“結果性教學”轉變為素養立意的“過程性教學”,這就要求學生不僅要知其然,更要知其所以然,同時應引導學生探究問題的“本源”,學會舉一反三,夯實數學基礎. 一方面,教師通過探尋幾何問題的本“源”,追溯數學思維發展的源泉,可以提升自身數學專業素養和專業水平[6];另一方面,教師把握幾何問題的“流”[7],登高望遠,拓展視野,可以培養學生思維的深度和廣度. 通過設置精致練習[8],摒棄“題海戰術”,提高學生學習數學的興趣,挖掘學習數學的潛能,促進數學綜合素養的提升[9].