基于IRS輔助MIMO通信的雙時間尺度信道估計

馬詩婷

（南京郵電大學 通信與信息工程學院，江蘇 南京 210003）

0 引言

多輸入多輸出（Multiple-Input Multiple-Output，MIMO）技術自提出以來一直在無線通信領域扮演著重要角色。然而，為降低硬件成本和能源消耗，未來需要更高能效的技術，因此智能反射面（Intelligent Reflecting Surface，IRS）以其低成本、低能耗的優勢脫穎而出［1-3］。IRS 是由低成本的大型無源反射元件組成的平面，每個無源元件可以獨立地反射接收到的信號并調整元件的相移，從而產生幅值和相移可重構的反射信號，以此增強有用信號或抑制干擾信號。然而，IRS 輔助通信的信道估計面臨比傳統通信場景信道估計更為嚴峻的挑戰。這是由于大多數IRS 采用全被動元素，僅配備了簡單的板載信號處理單元，只能反射電磁波，并不具備處理復雜信號的能力，難以獲取信道狀態信息（Channel State Information，CSI）。目前，大多數信道估計方法通過利用基站（Base Station，BS）和用戶設備（User Equipment，UE）的有源收發器估計出BS、IRS 與UE 之間的級聯信道，即BS-IRS-UE 級聯信道［4-5］。盡管大多數預編碼方案都是基于級聯信道的知識，但存在一些預編碼方案［6］需要BS-IRS 信道和IRS-UE 信道的單獨CSI。更重要的是，級聯信道估計方法的導頻開銷非常高，典型的IRS 輔助多用戶無線通信系統配有大的BS 天線、IRS 元件和UE。高導頻開銷在實踐中限制了頻譜效率并導致信道估計延遲，而對于高移動無線通信，這個問題可能更加嚴重，因此研究可以在短相干時間內進行準確信道估計的方法十分必要。

1 相關研究

目前關于IRS 輔助無線通信的研究有很多，例如文獻［6-11］均對聯合優化BS 處的預編碼矩陣和IRS 處的反射系數向量進行了研究，然而多用戶MIMO 的預編碼問題被證明是非凸的和NP-hard［9］的。因此，文獻［10-11］試圖為IRS 輔助的通信系統找到接近最優的聯合波束成形解決方案。此外，文獻［12-13］對IRS 輔助安全通信問題進行了探討。然而，在眾多相關研究中，針對IRS 輔助通信系統信道估計的研究還很有限。例如，文獻［4］提出一個時隙只開啟一個IRS 元件，成功地估計出IRS 元件的級聯信道。由于其他IRS 元件不發射導頻，因此信道估計精度會受到接收信噪比（Signal-To-Noise Ratio，SNR）下降的影響。文獻［5］設計了一系列反射系數向量，并實現了級聯信道的最小方差無偏（Minimum Variance Unbiased，MVU）估計，然而該方案的導頻開銷等于IRS 元件的數量乘以UE 的數量，限制了其在具有大量IRS 元件系統中的應用。文獻［14］提出一種在IRS 輔助MISO 通信系統的場景下利用雙時間尺度特性估計信道的方法，并顯著降低了平均導頻開銷，但只考慮了UE 單天線的情況，有一定局限性。文獻［15］提出一種巧妙的方法減少導頻開銷，首先估計一個UE 的級聯信道，并將其作為參考信道，然后利用不同UE之間信道的相關性估計其他UE 的級聯信道，但該方法在SNR 較低時信道估計不準確。文獻［16-17］利用IRS 信道矩陣的低秩特性構造聯合稀疏矩陣，并設計矩陣填充問題實現級聯信道估計。文獻［18］通過挖掘IRS 級聯信道的結構化稀疏特征提升信道反饋性能，顯著降低了信道估計開銷。文獻［19-20］使用深度學習技術解決信道估計問題。文獻［21］利用毫米波下大規模陣列的信道稀疏性減少導頻開銷。文獻［22-23］概述了IRS 輔助無線通信系統中信道估計的基本原理、解決方案和未來機會，并提出一種具有低導頻開銷的信道估計新方案。文獻［24］研究了IRS 信道的單結構稀疏性，并提出一種降維信道反饋方案，該方案具有較低的信道反饋開銷。

然而，以上文獻中的方法僅適用于低秩或稀疏信道的特殊場景，且存在信道估計實現復雜度過高、準確性較差等問題。為此，本文提出一種基于IRS 輔助的多用戶MIMO 上行無線通信的系統模型，利用信道的雙時間尺度特性分別估計BS-IRS 和 IRS-UE 之間單獨的信道狀態信息。仿真結果顯示，與多種已有方案相比，該方案降低了導頻開銷和歸一化均方誤差，具有一定優勢。

2 系統模型

本文建立的 IRS 輔助的多用戶MIMO 上行無線通信系統模型如圖1 所示，其由一個具有N個反射元件的IRS、1個配備MR根天線的BS和K個配備MT根天線的UE 組成。上行鏈路BS接收到的信號表示為：

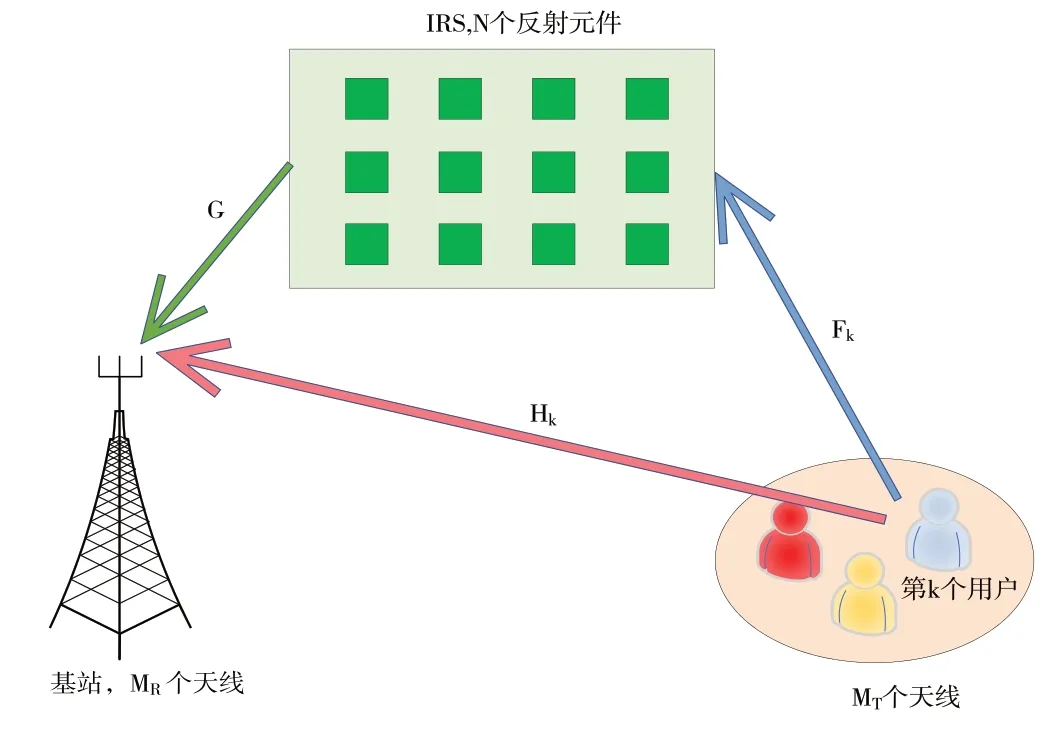
Fig.1 System model圖1 系統模型

3 準靜態BS-IRS信道估計

采用文獻［14］中提出的基于坐標下降的信道估計算法估計準靜態BS-IRS 信道。如圖2 所示，在估計信道G時，傳輸幀由(N+1)個子幀組成，每個子幀持續L個時隙。在第t個子幀中，IRS 處的反射系數向量為。在第m1個時隙中，第m1根BS 天線發送一個非零導頻，其余(MR-1)根BS 天線不發送導頻。其余BS 天線接收到的導頻可表示為：

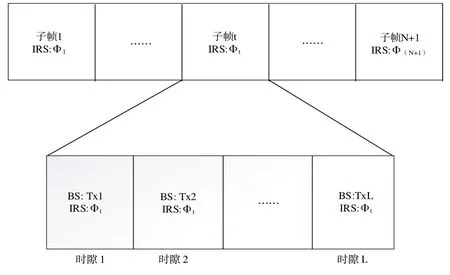
Fig.2 Large-timescale channel estimation frame structure圖2 大時間尺度信道估計的幀結構

以下分3 個階段估計準靜態BS-IRS 信道。首先將問題劃分為N個獨立的子問題，每個子問題為估計BS 與單個IRS 元件之間的信道；其次估計每個子問題的初始值；最后，通過坐標下降法迭代優化對BS-IRS 信道進行估計。

首先將問題分為N個子問題，表示為：

分別通過求解N個子問題估計準靜態BS-IRS 信道。對于給定的n，將第n個子問題表示為：

然后計算信道初始值，表示為：

最后利用坐標下降法迭代優化，在每i次外部迭代中，MR個信道的估計值都從第一個到最后一個進行迭代優化。第i次外部迭代信道估計值（具體證明詳見文獻［14］）表示為：

4 移動IRS-UE和BS-UE信道估計

使用傳統上行鏈路導頻傳輸方案［5］估計移動IRS-UE和BS-UE 信道。如圖3 所示，上行導頻傳輸幀由τ0個子幀組成，每個子幀持續K個時隙。在第t個子幀中，IRS 處的反射系數向量為，反射系數向量的元素從{ +1，-1}中隨機抽取。在一個子幀的K個時隙中，UE 發送上行導頻序列，即，k=1，2，…，K。

為了區分來自不同UE 的導頻，假設不同UE 發射正交導頻序列，即：

Fig.3 The uplink channel estimation frame structure圖3 上行鏈路信道估計的幀結構

在第t個子幀中，將多時隙導頻傳輸模型表示為：

5 導頻開銷分析

在準靜態信道估計中，BS-IRS 信道中有MRN個系數需要在大時間尺度上進行估計。本文使用(N+1)個子幀，每個子幀由L個時隙組成。為確保接收到的導頻數大于信道系數數量，需要L≥2。相關導頻開銷為τ1=(N+1)L，與L成正比。在移動信道估計階段，IRS-UE 信道中含有的NKMT個系數和BS-UE 信道中含有的MTKMR個系數均需在小時間尺度內估計。由于BS 在K個時隙的一個子幀中獲得MRK個導頻測量值，至少需要個子幀。因此，小時間尺度信道估計的導頻開銷為

在兩次信道估計方案中，準靜態BS-IRS 信道在大時間尺度上進行估計，因此需要根據BS-IRS 信道的估計頻率計算平均導頻開銷。具體地，令TL和TS分別表示大時間尺度信道和小時間尺度信道的信道相干時間，并且TL=αTS且α?1。在TS時間段內，平均導頻開銷計算為τ=當L=2 時，所需最小導頻開銷為

表1 為不同信道估計方案導頻開銷比較，其中：A 為本文方案；B 為采用級聯信道的最小方差無偏估計方案［5］；C為利用不同用戶信道之間相關性進行估計的方案［15］。

Table 1 Pilot overhead comparison of different channel estimation schemes表1 不同信道估計方案導頻開銷比較

圖4、圖5、圖6、圖7 分別為導頻開銷與BS 天線數MR、IRS 元件數N、UE 數K、UE 天線數MT之間的關系，其中α=4。在圖4 中，方案A 和方案C 的導頻開銷隨著BS 天線數增加而下降，這是由于BS 可以在具有更多天線的時隙中獲得更多上行鏈路導頻測量值，而方案B 的導頻開銷與BS天線數無關。圖5、圖6、圖7 結果表明IRS 元件數越多，UE越多，UE 天線數越多，需要的導頻越多。可以看出，方案A的導頻開銷略低于方案C，顯著低于方案B。

6 仿真結果與分析

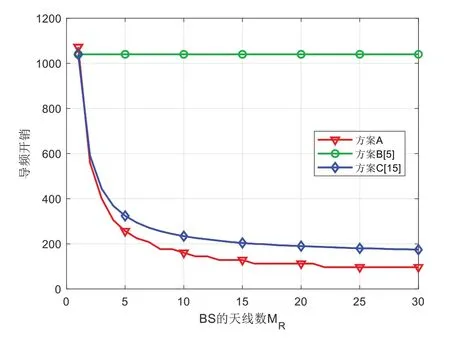
Fig.4 Relationship between pilot overhead and MR（N=64，K=8，L=2，MT=2）圖4 導頻開銷與BS天線數的關系（N=64，K=8，L=2，MT=2）

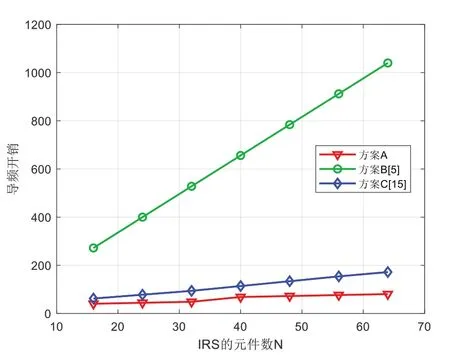
Fig.5 Relationship between pilot overhead and N(MR=32，K=8，L=2，MT=2 ）圖5 導頻開銷與IRS元件數的關系（MR=32，K=8，L=2，MT=2）

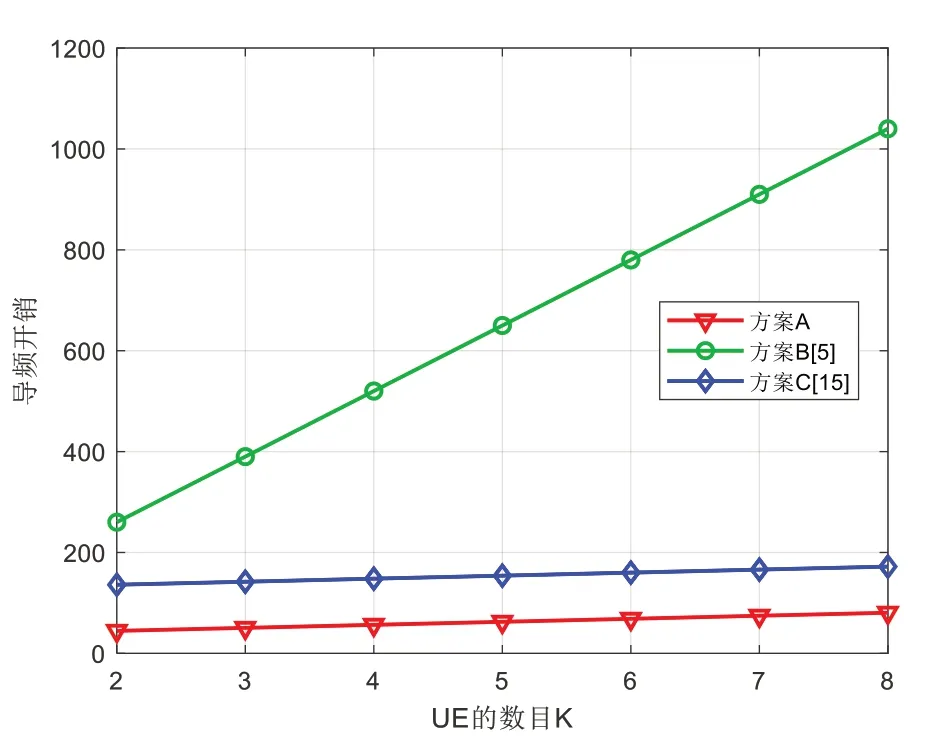
Fig.6 Relationship between pilot overhead and K(MR=32，N=64，L=2，MT=2）圖6 導頻開銷與UE數的關系（MR=32，N=64，L=2，MT=2）

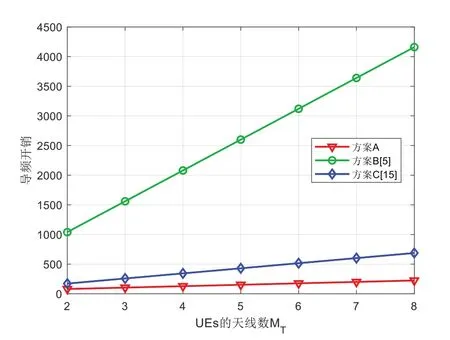
Fig.7 Relationship between pilot overhead and MT（MR=32，N=64，K=8，L=2）圖7 導頻開銷與UE天線數的關系（MR=32，N=64，K=8，L=2）

對于大時間尺度信道估計中的雙鏈路導頻傳輸，將信干噪比定義為：

對于小時間尺度信道估計中的上行導頻傳輸，將信噪比定義為：

NMSE 為歸一化均方誤差（Normalized Mean Square Error），用于評價預測值與實際值的擬合效果。其中，級聯信道的NMSE 定義為：

直接信道的NMSE 定義為：

圖8、圖9 分別為級聯信道和直接信道的NMSE 與上行SNRs的關系，可以看出二者的NMSE 均隨SNR 的變大而降低，且方案A 的NMSE 比方案C 更低。雖然方案B 的信道估計更準確，但這主要是由于其導頻開銷比方案A 高出一個數量級。

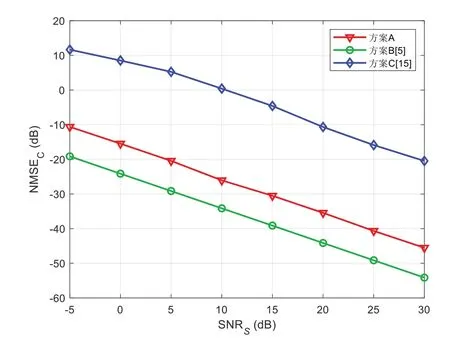
Fig.8 Relationship between NMSE for the cascaded channel and uplink SNRs圖8 級聯信道的NMSE與上行SNRs的關系

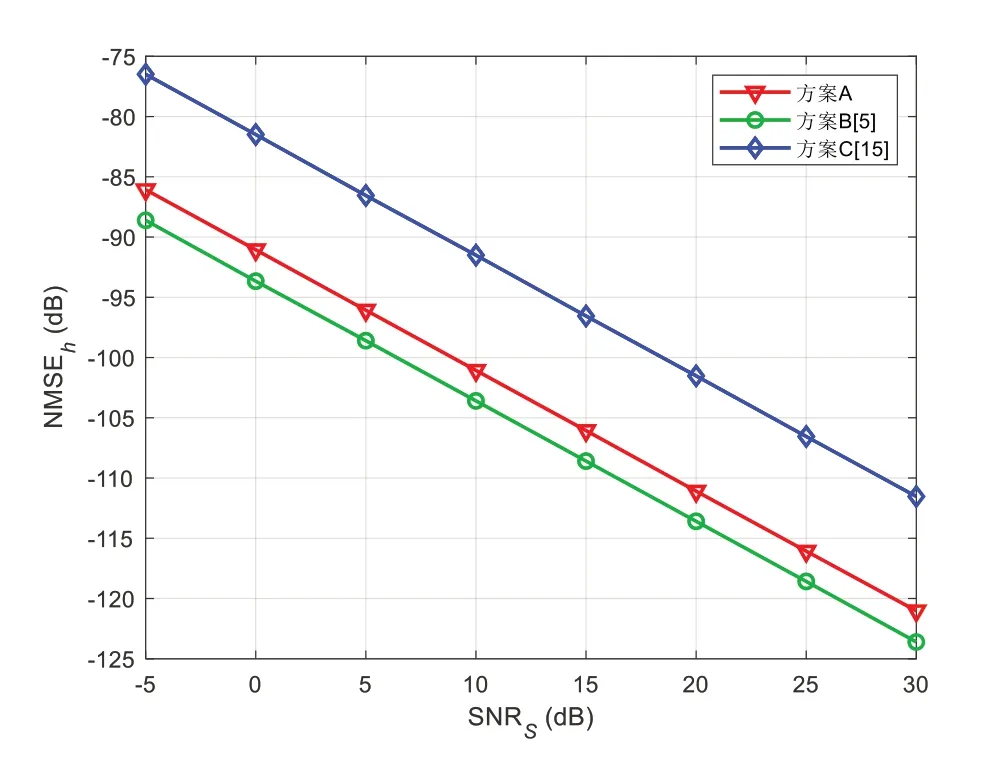
Fig.9 Relationship between NMSE for the direct channel and uplink SNRs圖9 直接信道的NMSE與上行SNRs的關系

7 結語

本文提出IRS 在多用戶MIMO 通信信道估計應用的新場景，利用信道的雙時間尺度特性進行信道估計，分別通過基于坐標下降的信道估計算法和最小二乘算法估計BS-IRS 信道和IRS-UE 信道，在低導頻開銷的情況下實現了信道的準確估計。今后IRS 輔助通信的信道估計還可以擴展到更加豐富的場景，例如：①當使用多個IRS 輔助無線通信時，尋找一種低導頻開銷的信道估計方法；②當IRS 輔助高速移動的無線通信時，尋找一種傳輸協議進行信道估計并緩解多普勒頻移。