無信控交叉口環境下考慮駕駛員誤差的集中式軌跡規劃*

錢立軍，陳 晨，陳 健

（1.合肥工業大學汽車與交通工程學院，合肥 230009；2.南昌理工學院機電工程學院，南昌 330044）

前言

隨著智能網聯汽車（connected and automated vehicle，CAV）技術的發展，車聯網背景下的交通規劃與控制方法已得到大量研究。交叉口是城市交通的重要節點，承擔各向車流的通行任務，大部分交通擁堵甚至安全事故發生于此［1］。在應用高等級自動駕駛汽車的智慧交通場景中，路側單元系統與中央控制器的結合可以有效代替傳統信號燈配時的交叉口管理方案。

在理想環境下交通系統中的車流全部由CAV構成，也是現有研究的通用前提。得益于CAV 的完全可控性，國內外學者已經取得了大量理論研究成果［2］。Dresner 和Stone 提出的“先到先行”原則是無信控交叉口控制的基礎。車輛向路端控制系統提出駛入申請，控制器根據各車道上的車輛位置進行順序分配［3］。

在后續混合交通領域發展中，基于“預約”的通行權高效化調配方法成為研究熱點之一。Yao 等［4］面向混合交通中的CAV，設計了以行駛時間和安全風險為復合目標的離散規劃策略。該策略可將求解時間縮短至10 s 以下，并在不同滲透率工況下均有較好的應用效果。陳一鶴等［5］面向混合交通環境，研究了CAV 滲透率對預約控制方法的影響。但是，這類方法關注靠近交叉口的部分車輛，對于遠端車輛并不管控，因此分布式控制效果與全局最優解相差較大。

另一方面，對交叉口范圍內的車輛進行集中式控制的方法也應用廣泛。柴琳果等［6-7］基于虛擬隊列的思想，將控制范圍內的所有車輛視為一個大規模隊列。該類方法旨在通過控制CAV 的方式影響整體交通性能，并且利用間隙理論建立混合跟車模型保證系統安全。在此基礎上，Chen 等［8］提出由CAV 作為領航車的“1+n”混合隊列，利用最優控制框架提高交叉口處的整體效率和燃油經濟性。

綜上所述，現有研究在進行混合交通的軌跡規劃問題時，普遍以OVM 和IDM 跟馳模型替代人類駕駛汽車（human driven vehicle，HDV），但是沒有考慮隨機性駕駛員誤差在車輛軌跡跟蹤階段的影響。本文中針對混合交通軌跡跟蹤階段中的駕駛員誤差現象，對無信控交叉口的集中式控制策略進行改進。以馬爾科夫鏈描述一定時長內的連續駕駛員誤差，并設計循環式的碰撞檢測框架。對于可能發生碰撞的情況，更新瞬時邊界條件后再次計算最優控制問題。采用重規劃策略調整車輛的跟蹤軌跡，提高混合車流在交叉口內部的安全性。最后，系統性地探討重規劃策略在不同流量、不同滲透率下的效果，分析重規劃過程對交通性能的影響。

1 方法概述

典型的單車道無信控交叉口場景如圖1 所示。以正東方向為x軸、正北方向為y軸、交叉口中心處為原點建立平面坐標系。其中，R為路端專用短程通信技術（dedicated short range communication，DSRC）范圍，r表示車道寬度。中央控制器布置于交叉口原點處，其通信范圍內所有車輛將進行多車協同規劃，而范圍之外的車輛保持自由駕駛。為方便描述，定義沿y軸正方向運動的車輛位于車道1，車道2～4按逆時針方向排布。

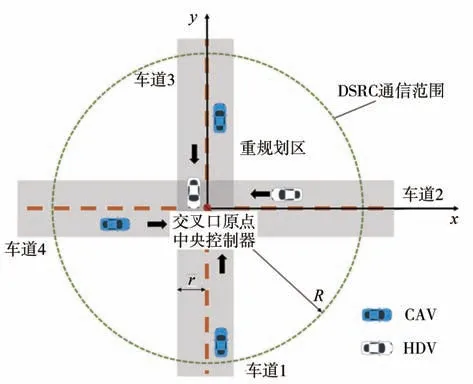
圖1 無信控交叉口示意圖

1.1 集中式重規劃框架

在集中式控制策略中，DSRC范圍內的所有車輛均被視為控制對象。受HDV 的影響，一次性規劃得到的軌跡無法保證后續的行車安全性，這表明按規劃速度進行運動的車輛間仍有危險。當前研究中，解決車輛軌跡跟蹤過程碰撞威脅的方法為對HDV的狀態估計。Zhou 等［9］提出一種簡約的射擊啟發式算法（shooting heuristic algorithm），在有限加速度條件下估計車輛軌跡的最大邊界，但是此類算法估計精度有限。Feng 等［10］基于車聯網信息實現對HDV的運動估計，使CAV 在恒定時間內實時計算軌跡，但其缺陷為計算量過大。

基于現有算法，本文針對混合交通中HDV 的駕駛員誤差估計，提出一種基于碰撞威脅的觸發式重規劃框架。如圖2 所示，根據時域遞進順序，任意車輛駛過交叉口的過程可劃分為以下4個步驟。

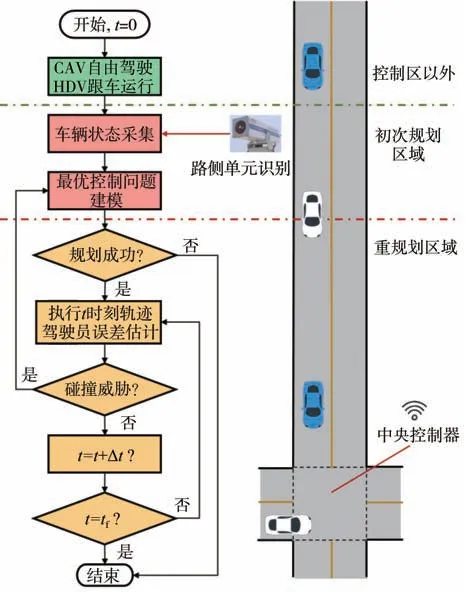
圖2 重規劃框架示意圖

步驟1：自由駕駛。位于控制區以外的車輛將自由駕駛，其中CAV 將保持勻速直線運動，而混合交通中的HDV 則根據智能駕駛員模型進行自主跟車運動［11］。

步驟2：狀態觀察。車輛進入交叉口控制范圍時，首先由路側單元觀察其位置、速度等狀態參數，并且對控制區內的所有車輛進行初次軌跡規劃。

步驟3：軌跡跟蹤。各車輛按計算得到的初始軌跡進行運動，并且根據HDV 的駕駛員誤差模型進行軌跡執行誤差估計。若估計時域內可能發生碰撞，則以初始軌跡為參考值進行多車協同重規劃。

步驟4：發生碰撞或駛離交叉口。在最后一次規劃之后，將生產兩類計算終止條件：（1）車輛運動至規劃終止時刻，且所有車安全離開控制區，回復自由駕駛狀態；（2）隨機誤差導致軌跡規劃失敗，控制區內出現無法避免的碰撞事故。

經過上述步驟，控制區內的所有車輛均在運動過程中收到一段或多段軌跡的持續性引導，且中央控制器將在不同約束條件下進行多次軌跡規劃計算。

1.2 離散最優控制

在步驟2和步驟3中，用于軌跡初次規劃或重規劃的Bolza型最優控制問題，可以總結為一種考慮末值性能函數的標準格式：

式中：根據文獻［12］中所示車輛運動學模型，z(t)表示系統的狀態變量集合，包括車輛坐標(x，y)、車身姿態角、速度和前輪擺角；u(t)表示系統的控制變量集合，包括車輛加速度和前輪轉向角速度；泛函Γ(·)包含了邊界約束和路徑約束；t0為初始時間；tf為終止時間。

采用離散優化法高斯偽譜法（Gauss pseudospectral method，GPM）將原始最優控制問題進行轉化，即使用多項式插值擬合的方式來接近原始最優控制問題的最優解。GPM 插值多項式的構造范圍為[-1，1]，為此引入一個新的時間變量τ∈[-1，1]，其構造式為

此時，式（1）中的系統微分方程約束可以轉化為

在此基礎上，可采用一個H階多項式擬合系統的狀態變量和控制變量，即

該多項式中的擬合點也被稱為Legendre-Gauss配點。由此，z(t)和u(t)可近似表示為

2 最優控制問題建模

2.1 最優控制目標

在控制區中，車道L 上第k輛車的位置可由其后軸中心點坐標表示，且行車速度、加速度分別為在時域系統中，該車輛在任意時刻t下的瞬時軌跡定義為

其中，橫縱坐標值、速度為狀態變量，加速度為控制變量。對于一個由n輛車組成的規劃系統，可構建Bloza型最優控制問題。對于交叉口工況，選擇交通效率、燃油經濟性、行程延誤構建復合優化目標：

式中：n為車輛總數；Δt為計算步長表示第i輛車的瞬時燃油消耗率，其取值為

式中：ms為車輛的對數穩態燃油消耗率；mc為車輛瞬態油耗與穩態油耗比值的對數；Te為發動機輸出轉矩；ωe為發動機轉速；βp，q、α0～α6為模型系數，取值方法依據文獻［14］。

此外，以駛離交叉口的時間為標準，各車的行車延誤定義為實際行駛耗時與自由駕駛耗時的差值。由此，車輛平均延誤時間的取值為

式中：tout，i為第i輛車實際駛離交叉口的時間；v0為車輛的初始車速，且當車輛不受控制時將保持速度為v0的勻速運動；di為第i輛車初始位置到交叉口中心的距離，其表達式為

2.2 約束條件

確定優化目標后，需根據各車輛的駕駛任務及交叉口環境建立不等式約束條件。對于不同行駛方向的車輛而言，其邊界約束條件為

式中：vmax為允許的最大速度；amax為最大加速度；B為車輛行駛邊界區間的集合，具體表達式為

式中w為車輛橫向寬度。對于一個多車協同系統，其規劃重點和前提條件在于車輛間的安全性。在本文研究的單車道交叉口環境中，車輛安全性可分解為兩個部分：同車道的前后車輛間應預防追尾、不同車道的車輛應避免在交叉口內部發生側碰事故。根據此定義，車輛間的安全距離約束不等式為

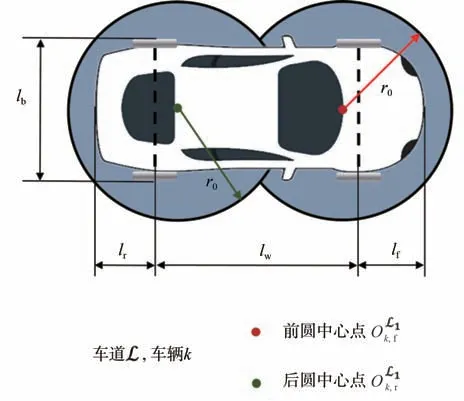
圖3 車輛雙圓模型

基于式（7）～式（14），可建立以obj為最小化目標的最優控制問題。采用GPM 對最優控制問題進行求解后，即可獲得[0，tf]時域內以Δt為時間間隔的n輛車軌跡集合。

3 駕駛員誤差分析

求解上述最優控制問題所得到的軌跡值被定義為理論軌跡，可通過人機交互界面（human-machine interface，HMI）輸出作為輔助駕駛員操作的建議數值。在混合交通環境中，CAV 通常被假設為沒有執行系統誤差，而HDV 則無法避免由駕駛員因素引起的軌跡跟蹤偏差。因此，須在理論軌跡的基礎上，分析駕駛員誤差產生的影響。

3.1 行車數據采集

為了獲得實際的人類駕駛誤差數據，設計了相關實車駕駛試驗。在試驗人員方面，共邀請年齡為25～45 歲、駕齡為1～7 年的駕駛員12 名（其中女性駕駛員3 人）參與試驗。在試驗場地方面，選擇合肥市某開放道路中的直線輔道路段，且在無社會車輛干擾時開展試驗。共設計以下3類試驗工況。

工況1：連續交叉口通行。根據文獻［16］中設計的隨機模型預測控制算法，基于2 個以上的連續信號燈信息進行生態駕駛速度規劃。

工況2：循環加速與減速。參考車輛循環工況中的加速、恒速、減速模塊，設計適用于測試用車的循環試驗。

工況3：無信控交叉口通行。根據文獻［17］中設計的無信控交叉口管理策略，計算多車協同下的車輛行駛軌跡。根據虛擬-現實結合手段，選擇任意車輛軌跡值為速度跟蹤對象開展試驗。

如圖4 所示，車載HMI 可展示當前時刻下的理論速度值、信號燈計時、道路允許車速等參數。在駕駛試驗過程中，車輛須在當前車道內穩定行駛。要求所有駕駛員關注車輛儀表與HMI 提示的理論值，并通過控制加速踏板和制動踏板的方式實現車速跟蹤。由車載上位機記錄車輛運行數據，且每位駕駛員在各工況下成功完成試驗3次以上。

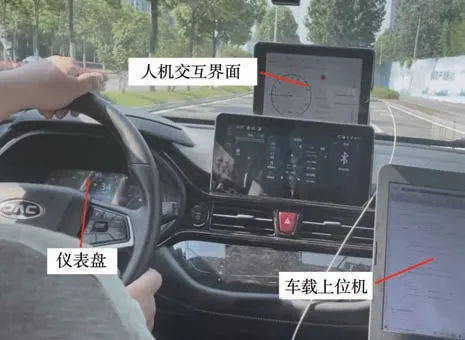
圖4 駕駛試驗示意圖

3.2 駕駛員誤差馬爾科夫鏈

根據上述試驗中采集的實際駕駛數據，開展駕駛員誤差分析。現有研究中駕駛員誤差的表達方式主要有兩類：實際車速或加速度與理論數值的差，且需要將誤差值離散為總數有限的狀態量。駕駛員誤差具有隨機性，同時誤差觀測方式符合馬爾科夫特性［18］，即當前時刻下的誤差值ε(t)決定了下一時刻的誤差值ε(t+1)。基于此，建立以加速度值為誤差的馬爾科夫鏈概率轉移矩陣。

式中：P為概率轉移矩陣；N為駕駛員誤差值狀態總數；pm，s為狀態轉移概率，可表示為

式中：m，s∈[1，N]?N+。根據概率完備性要求，有

3.3 考慮誤差的碰撞估計

根據式（15）可知HDV 的軌跡跟蹤誤差會引起車輛間相對位置的改變，在具有碰撞隱患的情況下將有必要實施軌跡重規劃。然而，執行式（7）～式（14）的軌跡規劃過程所需時間普遍大于系統執行步長Δt。為了提高規劃算法實時性，提出一種考慮駕駛員誤差的固定時域碰撞檢測方法。離散系統中任意HDV在t時刻下的位置參數為

式中為等效時間參數。在此基礎上，對所有HDV的位置進行估計后須判斷任意2 輛車的矩形外輪廓是否有重疊，則車輛k和車輛j之間的安全條件應滿足：

式中：點Aj～點Dj分別為車輛輪廓的4 個角點；點Pk為車輛k的任一角點；SΔ和S□分別為三角形和矩形面積［19］。由于式（18）中的車輛矩形輪廓包含于式（14）中的雙圓模型輪廓，故車輛的碰撞預測條件更為嚴格。

當車輛安全運動至任意時刻t，以ts為估計時間長度，判斷時域(t，t+ts]內是否有事故產生。若所有車輛均安全，則執行下一時刻軌跡；若發生碰撞，則以下t時刻的軌跡P(t)為規劃初值，保留約束條件后進行重規劃計算。

4 仿真結果與分析

為了檢驗重規劃架構在混合交通下的控制效果，設計了多種仿真工況。首先，在固定自動駕駛滲透率情況下分析多車協同運動軌跡，并檢驗車輛間安全性和重規劃的觸發過程。其次，以滲透率為變量分析不同混合交通比例下的重規劃次數和成功率。最后，對行程延誤和燃油經濟性等交通性能指標進行對比。

不同仿真工況下通用的車輛模型和環境參數如表1所示。

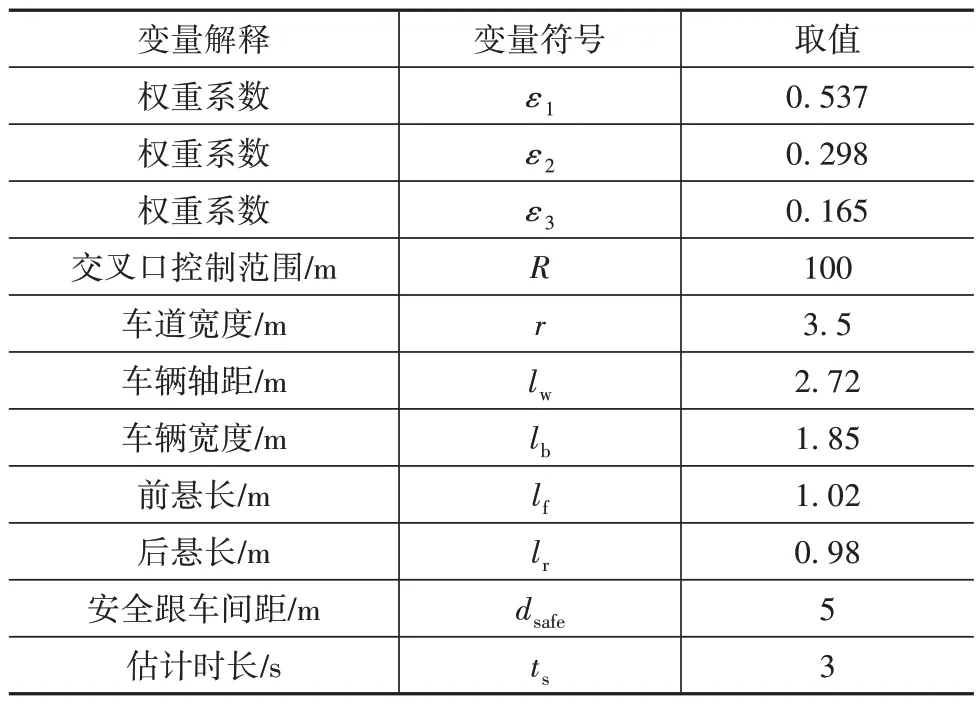
表1 車輛及環境參數

4.1 車輛運動過程分析

通過對實車駕駛數據的分析，獲得的馬爾科夫鏈概率轉移矩陣如圖5 所示。駕駛員誤差等級共分9級，分布范圍為［-0.4，0.4］。在各誤差等級下，轉移概率最大值均出現在對角線處。轉移矩陣峰值出現在ε(t)=0→ε(t+Δt)=0 處，其概率約為58%。且由于駕駛員操作連貫性，相鄰時刻的誤差值跨度越大，則其發生的概率越低。

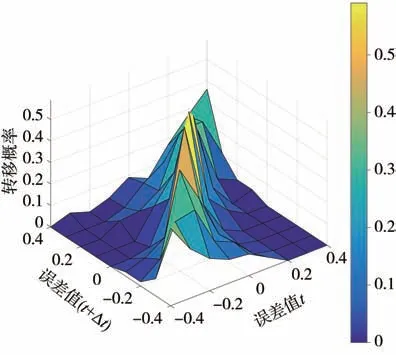
圖5 駕駛員誤差概率轉移矩陣三維圖

為檢驗重規劃框架對駕駛員隨機誤差的修正效果，共選擇10 輛車進行集中控制。其中，HDV 占比為50%，且車輛初始位置數據采集自Vissim 軟件。仿真時，必要的參數取值為：vmax=40 km/h，amax=5 m/s2，dsafe=5 m，并且車輛的運動初始速度v0=vmax。各車輛初始分布狀態及其種類如表2 所示，并根據初始位置的先后對其排序。

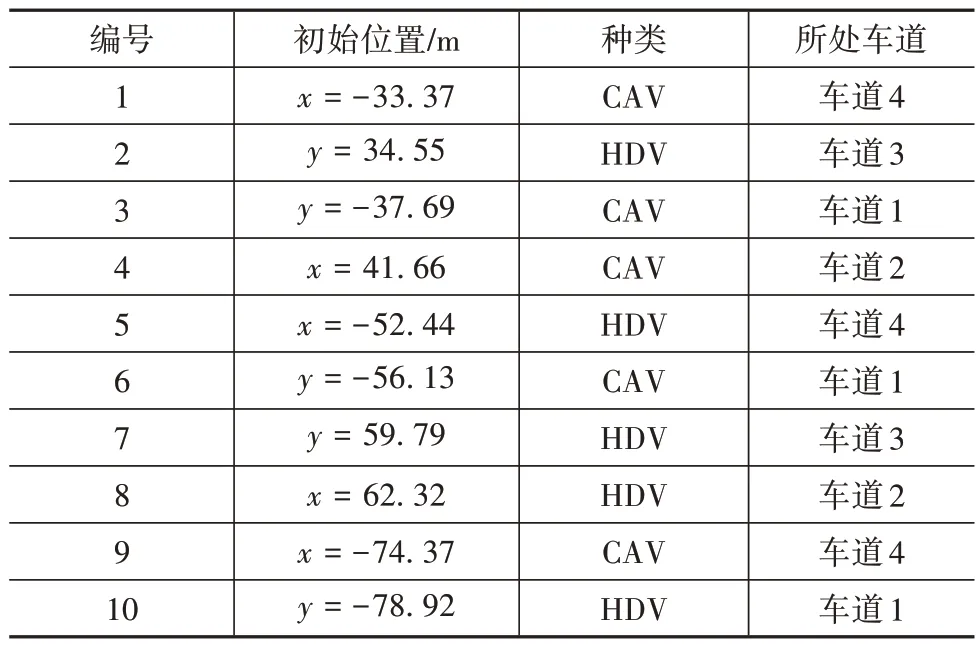
表2 車輛初始分布狀態及種類

10 輛車的運動軌跡如圖6 所示，其中車道1 至車道4 上的車輛分別采用實線、虛線、點劃線和雙點劃線表示。集中式規劃開始約10.5 s后，所有車輛均位于交叉口30 m以外，視為安全駛離。此時，所有車輛的通行順序依次為：車輛3-車輛1-車輛2-車輛4-車輛6-車輛5-車輛7-車輛8-車輛10-車輛9。可以看出，為了滿足式（7）的最小化要求，集中式規劃的結果不同于先到先行（first come first serve，FCFS）的原則，車輛的通行順序將不同于初始位置順序。

圖6 車輛軌跡圖

由于HDV 的影響，集中式規劃過程中共觸發2次重規劃計算，重規劃前后的部分車輛相對位置如圖7 所示。首先，車輛跟蹤初始軌跡運動約3.0 s時，中央控制器根據誤差傳遞鏈估計第5.1 s 時，車輛2 和車輛4 在交叉口中心處將發生側碰，見圖7（a）。進行第1 次重規劃后，此次碰撞隱患消除。其次，車輛對新軌跡的跟蹤過程中，車輛9和車輛10可能在運動開始第7.6 s 時發生碰撞，由此觸發第2 次重規劃計算后隱患消除（如圖7（b）所示）。

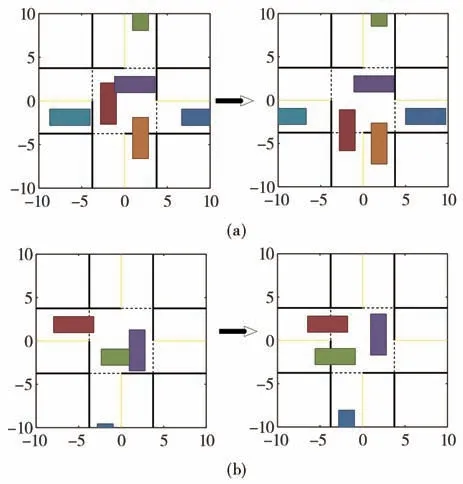
圖7 重規劃前后車輛位置對比

為了體現重規劃后的安全性能，圖8 展示了運動全程中的車輛間距。如圖8（a）所示，當車輛位于相鄰車道時，其間距曲線呈現出交叉口環境中典型的V字型特征。由圖8（b）可知相同車道內的車輛間保持了足夠的安全車距，且所有車輛間的間距均為正值，表明無碰撞事故發生。

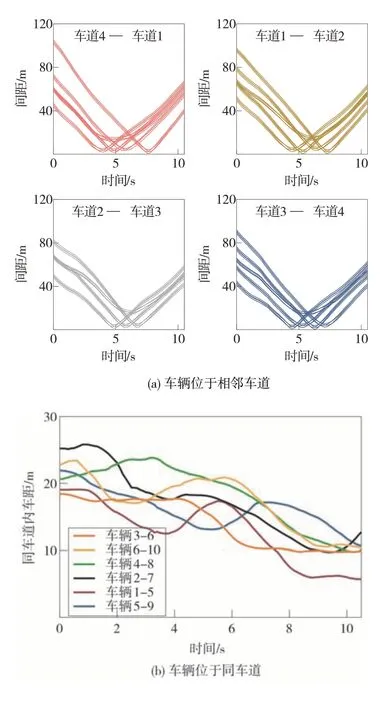
圖8 運動全程車間距

4.2 重規劃效果分析

為了驗證自動駕駛比例對規劃過程的影響，在隨機的車輛初始分布狀態下，改變自動駕駛滲透率后進行多次仿真試驗，直至規劃成功次數達到400次后停止。

統計各滲透率工況下仿真成功率如表3 所示。在完全由HDV 構成的車流中，有10%左右的概率計算失敗。并且，當交通環境中CAV 比例高于HDV時，事故發生率將控制在5%以下。而當自動駕駛占比提升至70%以上時，集中規劃成功率可高于98%。

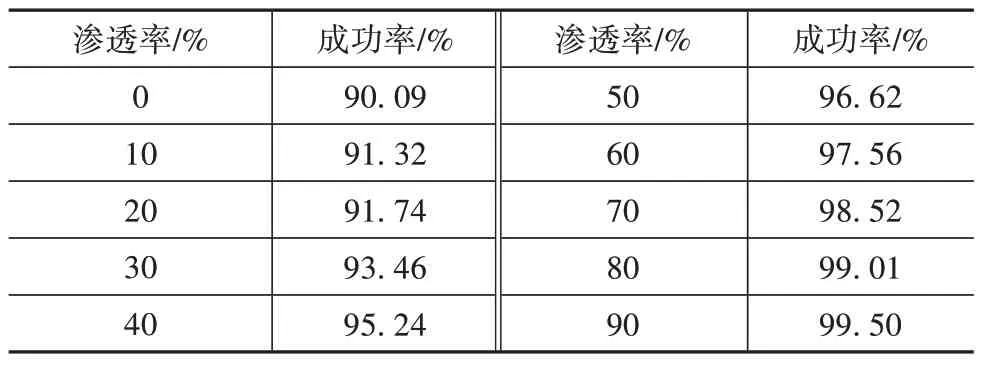
表3 仿真成功率統計結果

在此基礎上，分析各滲透率工況下的重規劃計算情況。如圖9 所示，完全HDV 工況下有約90%的計算過程都需要進行重規劃處理，且有15%左右的計算中進行了3次重規劃操作。隨著CAV 比例的提升，單次規劃的成功率逐漸提升。并且，當滲透率高于60%時，多數情況下進行1 次重規劃即可消除駕駛員誤差的影響。但是，即使CAV 滲透率到達90%，初次規劃的成功率仍只有約60%。

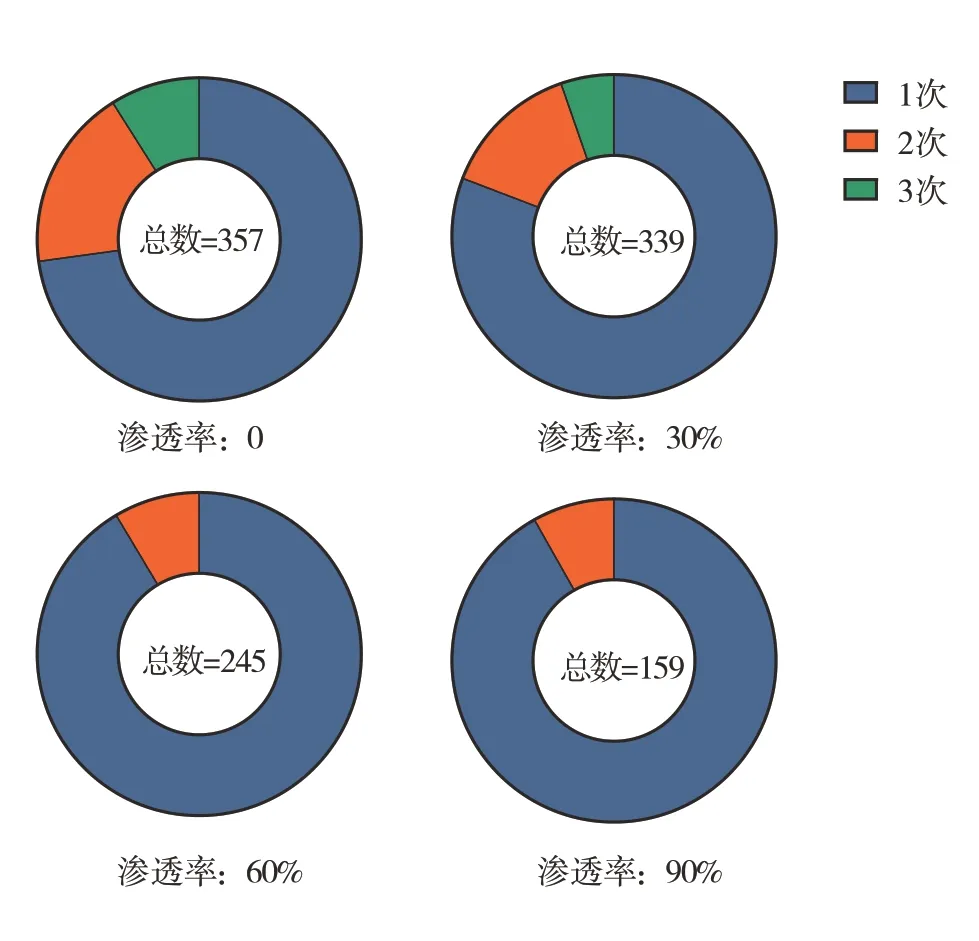
圖9 重規劃次數統計結果

集中式方法雖可以獲得接近全局最優解的計算結果，但其求解過程耗時較長。為分析重規劃實時性，以被控車輛數目和交通滲透率為變量，統計重規劃的平均計算時間。如圖10 所示，隨著車輛數目的增長重規劃耗時由約0.5 增大至約1.5 s，且10 輛車工況下平均耗時為0.7 s左右。此外，滲透率對計算時間影響不大，是因為最優控制問題中HDV 與CAV采用的運動學模型和約束條件均一致，即軌跡求解時并不考慮車輛類型。但是，總體而言集中式重規劃方法的實時性仍不足。

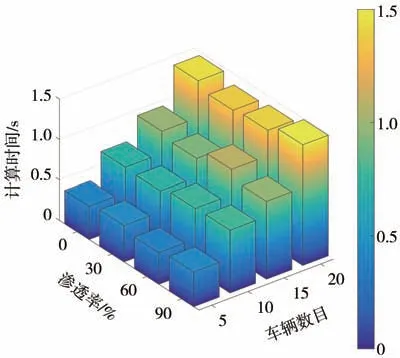
圖10 重規劃耗時統計結果

4.3 交通性能對比

最后，為了體現最優化算法的約束效果，選擇傳統虛擬隊列方法作為對照，以完全自動駕駛工況作為參考，比較不同滲透率下的車輛平均燃油經濟性和行車延誤指標。

如圖11 所示，由于HDV 的影響，集中式規劃方法中的燃油消耗量相比于全CAV 工況增長了3.03%～14.57%，而行車延誤時間也提高了0.14～0.45 s。然而，隨著自動駕駛滲透率的提升，交通性能指標均可得到改善。此外，由于最優化指標中包含了燃油經濟性和行車延誤參數，故整體交通性能指標均優于傳統的虛擬隊列方法。具體地，所提方法中的車輛平均延誤僅為對比方法的60%左右，且受滲透率變化的影響較小，這體現了集中式規劃的結果更近似于全局最優解。

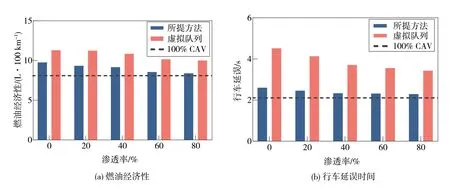
圖11 交通性能對比結果

5 結論

本文面向無信控交叉口環境，提出一種考慮駕駛員誤差的集中式軌跡重規劃方法。

首先，設計了面向無信控交叉口的集中式軌跡規劃框架，以運動總時間、燃油消耗、行車延誤等復合指標作為優化目標，并根據交叉口環境參數建立邊界約束條件。在此基礎上，基于HDV 誤差和車輛輪廓相交判別式設計重規劃觸發條件。

其次，通過實車駕駛試驗，在不同輔助駕駛測試工況下獲得多位試驗員的操作誤差數據，并根據誤差分布等級建立傳遞矩陣，并驗證了重規劃的可行性和安全性。

最后，統計了仿真結果，分析了自動駕駛滲透率對重規劃次數的影響，驗證了規劃成功率可達90%以上。并且將所提方法與傳統虛擬隊列方法進行比較，結果表明采用集中式規劃方法將可獲得更優的交通性能指標。但是，所提方法在低滲透率工況下的失效率仍過高，這也是后續研究的改進方向。