一類具有隔離項的時滯分數階SIQ傳染病模型的穩(wěn)定性分析

王娜

( 山西工商學院 計算機信息工程學院, 太原 030006 )

0 引言

很多傳染病(如霍亂、傷寒、流感、肺結核、艾滋病、鼠疫等)會嚴重危害人類的健康,因此做好預防工作具有重要意義.目前,已有許多國內外學者利用分數階微積分建立了傳染病模型,并對模型的穩(wěn)定性和分岔等動力學特性進行了研究.例如:Mousa Mohamed等[1]建立了一個關于兒童疾病(麻疹、腮腺炎、水痘等)的分數階“易感-感染-恢復”SIR模型,并定性考察了該模型的動力特性.Karaji等[2]建立了一個分數階乙型肝炎流行模型,并利用分數階Barbalat引理研究了該模型的全局動力學.Miao等[3]在分數階SIRS傳染病模型中引入了兩種不同的耦合控制器,并利用不動點定理研究了Julia集的復雜性和不規(guī)則性.Wang等[4]提出了一類帶有飽和方程的時滯分數階SIR傳染病模型,并在任意時滯下分析了模型的穩(wěn)定性與分支情況.在上述研究的基礎上,為了進一步探討引入時滯對分數階傳染病模型的動力學特性的影響,本文建立了一類具有隔離項的時滯分數階SIQ傳染病模型,并研究了其動力學性質.

1 預備知識

定義1[5]連續(xù)函數f:(0,+∞)→R的α(α>0)階Caputo分數階導數為:

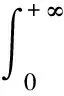
引理1[6]Caputo分數階導數的Laplace變換為:

引理2[7]已知時滯分數階系統:

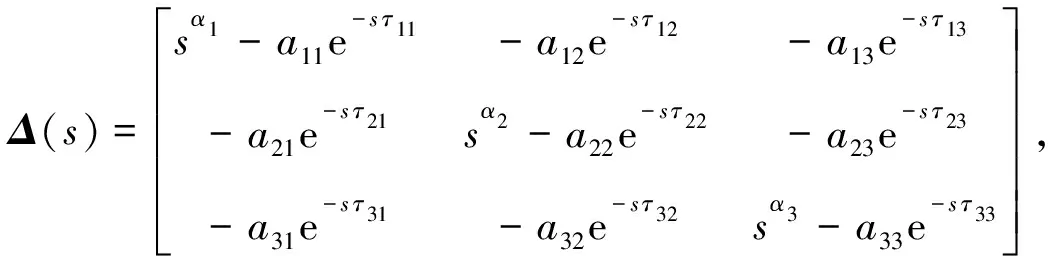
引理3[8](Routh-Hurwitz判據)已知一元多項式方程λn+a1λn-1+a2λn-2+…+an-1λ+an= 0,其所有的根均具有負實部的充要條件是:

2 具有隔離項的時滯分數階SIQ傳染病模型的建立

文獻[9]的作者建立了如下一類具有隔離項的常微分SIQS的傳染病數學模型:

(1)

其中:S(t)、I(t)、Q(t)分別為t時刻人群中的易感染者、感染者、隔離者人數……