水泥砂漿面層加固砌體墻抗震可靠指標研究

吳樂樂,唐曹明,2,羅開海,2,黃世敏,2,羅 瑞,程紹革,2

(1.中國建筑科學研究院,北京 100013;2.住房和城鄉建設部防災研究中心,北京 100013;3.北京城建-其士建筑聯營,北京 100080)

0 引言

我國砌體房屋存量巨大,隨著城市更新進程的不斷推進,對老舊的砌體房屋進行加固升級以滿足功能需求和抗震設防的要求成為一項重要的工作。水泥砂漿面層加固是砌體房屋加固的一種常見且簡單高效的方法[1-2]。《砌體結構加固設計規范》(GB 50702-2011)(簡稱“規范”)[3]和《建筑抗震加固技術規程》(JGJ 116-2009)(簡稱“規程”)[4],均給出了水泥砂漿和鋼筋網水泥砂漿面層加固方法及驗算公式。然而“規范”與“規程”的驗算結果卻大相徑庭[5-6]。在水泥砂漿面層和鋼筋網水泥砂漿面層加固砌體結構方面,不少學者進行了理論和試驗研究。黃忠邦[7]對水泥砂漿和鋼筋網水泥砂漿面層加固磚砌體進行了試驗研究,結果表明：采用水泥砂漿抹面加固墻體可提高抗剪能力約1倍,采用鋼筋網水泥砂漿抹面加固墻體可提高抗剪能力2倍以上;蘇三慶等[8]對夾板墻進行了低周反復荷載作用下的試驗研究,指出夾板墻加固磚墻可以提高墻體的抗震能力,并建議抹面砂漿與樓地面進行可靠連接;許清風等[9]對采用舊房拆下的八五磚并用黏土石灰砂漿砌筑的8片墻進行了鋼筋網水泥砂漿加固試驗研究,研究表明：雙側鋼筋網水泥砂漿加固舊磚墻,不僅可以提高抗震能力還可大幅提高受壓承載力;李明等[10]對8片鋼筋網砂漿抹面加固的低強度砂漿磚砌體墻進行了抗側力對比試驗研究,研究表明：采用鋼筋網砂漿抹面加固后,可顯著提高墻體的初裂荷載、極限荷載和剛度,同時豎向壓力越大,墻體的位移延性比越小,剛度越大;羅瑞等[11-13]和唐曹明等[14]對4組共12片砌筑砂漿強度等級低于M2.5的低強度磚墻進行了擬靜力試驗,并對水泥砂漿面層加固方法的適用性進行了分析,研究表明：水泥砂漿及鋼筋網水泥砂漿加固后可改善原磚墻的脆性破壞模式,提高受剪承載力、變形和耗能能力,高應力條件下(應力不小于0.6 MPa),面層厚度對抗震能力影響明顯且面層鋼筋網即使不錨入地梁也能屈服。通過上述研究可知：目前對鋼筋網水泥砂漿面層加固的研究主要聚焦在加固墻體的抗震性能、破壞模式和強度增強系數方面,而鋼筋網水泥砂漿面層加固的抗震可靠度研究還很少。本文將對“規范”與“規程”的可靠度進行分析研究,并進行10片未加固低強度磚墻和20片單面水泥砂漿和鋼筋網水泥砂漿面層加固低強度磚墻的擬靜力試驗研究,給出適用于水泥砂漿面層加固磚墻的抗震驗算公式和對應的抗震可靠指標。

1 砂漿面層加固磚墻的增強系數

規程：采用水泥砂漿面層和鋼筋網砂漿面層加固墻體的設計時,原砌體實際的砌筑砂漿強度等級不宜高于M2.5,面層的砂漿強度等級宜采用M10,鋼筋網片宜采用φ6@300,此條件下原墻厚240mm加固后的抗震能力基準增強系數見表1。

表1 規程面層加固的基準增強系數Table 1 Benchmark improvement coefficient of JGJ 116-2009

面層加固后各墻段抗震能力的增強系數可按式(1)計算：

(1)

式中：ηPij為第i樓層第j墻段面層加固的增強系數;η0為基準增強系數,磚墻體按表1采用;tw0為原墻體厚度;fvE為原墻體的抗震抗剪強度設計值。

規范：采用鋼筋網水泥砂漿面層加固法加固砌體構件時,對磚砌體,其原砌筑砂漿強度等級不宜低于M1,但若為低層建筑,允許不低于M0.4,加固后的砌體墻的抗震受剪承載力如式(2)所示：

(2)

式中：VME這為原砌體抗震受剪承載力,按現行國家標準《砌體結構設計規范》(GB 50003-2011)[15]的有關規定計算確定;Vsj為采用鋼筋網水泥砂漿面層加固后提高的抗震受剪承載力;γRE為承載力抗震調整系數,取γRE為0.9,此系數與《建筑抗震設計規范》(GB 50011-2010)(簡稱抗規)[16]中的承載力抗震調整系數不同,為避免與抗規混淆,抗規中承載力抗震調整系用γRES表示。

采用手工抹壓施工的鋼筋網水泥砂漿面層加固后提高的受剪承載力Vsj按式(3)計算：

Vsj=0.02fbh+0.2fyAs(h/s)

(3)

式中：f為面層砂漿軸心抗壓強度設計值,M10砂漿軸心抗壓設計值為3.4 MPa[3];b為砂漿面層厚度;h為墻體水平方向長度;fy為水平向鋼筋的設計強度值;As為水平向單排鋼筋截面面積;s為水平向鋼筋的間距。

按規范中墻體抗震受剪承載力換算的增強系數如式(4)和式(5)所示：

(4)

(5)

規程與規范中fvE=ξNfv,ξN為正應力影響系數,如式(6)所示：

(6)

式中：fv為抗剪承載力設計值;σ0為對應于重力荷載代表值的砌體截面平均壓應力。

2 水泥砂漿面層加固磚墻的可靠度分析

2.1 可靠指標計算

加固前墻段抗震驗算的功能函數如式(7)所示：

(7)

式中：γG為重力荷載分項系數;SGE為重力荷載代表值;γEh為水平地震作用分項系數;SEhk為水平地震作用標準值的效應。

按規程加固后的墻段抗震能力驗算如式(8)所示：

(8)

式中：A為墻段截面面積。

按規程加固后墻段抗震驗算的功能函數如式(9)所示：

(9)

按規范加固后墻段抗震驗算的功能函數如式(10)所示：

(10)

加固后磚墻的抗震可靠指標可如式(11)所示,各變量的分布特征見表2[17-19]。

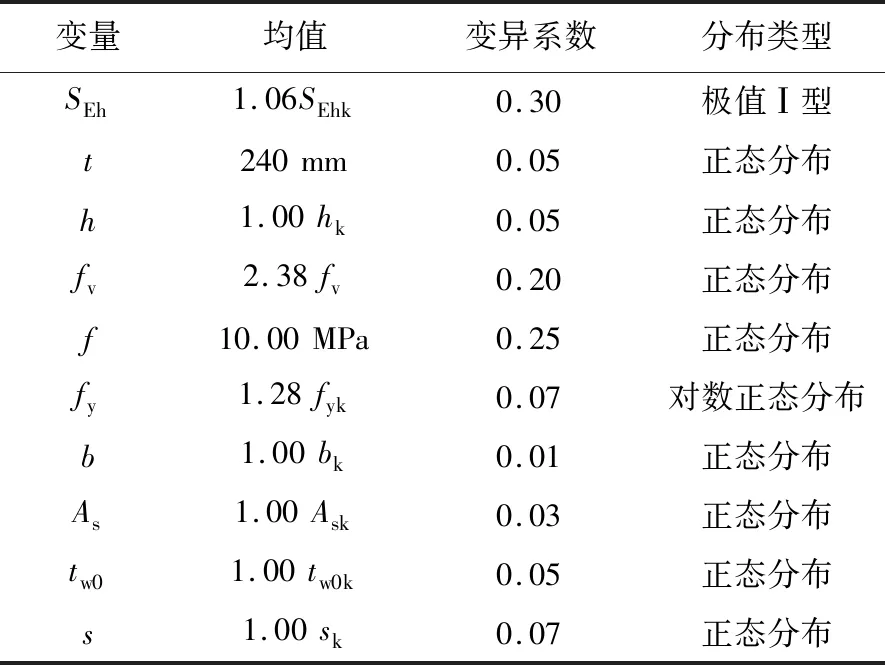
表2 各變量統計特征Table 2 Statistical characteristics of each variable

β=-Φ-1(Pf{g(x)<0})

(11)

式中：Pf{g(x)<0}為構件失效概率;Φ-1(·)為標準正態分布函數的逆函數。

本文采用蒙特卡洛一般抽樣的方法計算可靠指標,加固后結構的可靠指標提高值由Δβ表示,Δβ=βafter-βbefore,其中：βbefore為原砌體墻抗震可靠指標;βafter為加固后砌體墻抗震可靠指標。Δβ與增強系數ηPij類似,可以反映加固后墻體抗震性能的變化規律。

根據表1中給出的面層厚度、砂漿強度等級、配筋、單雙面加固條件和表2中變量的分布特征,按照式(7)、式(9)-式(11)計算“規范”和“規程”中水泥砂漿面層加固前后的抗震可靠指標提高值Δβ的步驟如下：

1)根據式(7),令gbefore=0(對砌體墻抗震驗算時僅考慮水平地震作用效應),計算水平地震作用效應標準值SEhk;

2)根據式(7)和表2中變量統計特性計算原砌體墻抗震失效概率Pfbefore;

3)將SEhk帶入式(9)和式(10),根據表2中變量統計特性分別計算按照“規程”和“規范”加固后失效概率Pf1after和Pf2after;

4)根據式(11)分別計算加固前可靠指標βbefore、按“規程”和“規范”加固后可靠指標β1after和β2after;

5)計算按規程和規范加固后的可靠指標提高值Δβ=βafter-βbefore。

2.2 規范與規程抗震可靠指標

加固后可靠指標提高值Δβ如圖1-2所示,Δβ整體的變化規律與文獻[6]中增強系數的變化規律一致。規程與規范的抗震可靠水平差別較大。不同砂漿強度等級下,規程的Δβ離散程度高于規范,隨著豎向壓應力的提高規范中不同砂漿強度等級的Δβ趨于一致。隨著砂漿強度等級的提高,規程與規范的Δβ差異明顯減小。當砂漿強度等級為M2.5時,按規程計算的可靠指標提高程度非常有限,甚至出現負增長情況,這反映出規程公式的不合理性。對比240 mm墻體和360 mm墻體加固后的Δβ可以發現：360 mm墻體的Δβ普遍低于240 mm墻體,這也說明水泥砂漿面層加固更適用于240 mm厚的磚墻。

3 單面水泥砂漿面層加固低強度砌體墻試驗研究

3.1 試驗概況

課題組對10片未加固低強度磚墻(簡稱“未加固墻”)和20片單面水泥砂漿面層加固低強度磚墻(簡稱“加固墻”)進行了擬靜力試驗,試件幾何模型如圖3所示。磚強度等級為MU10,砌筑砂漿強度等級分別為M0.4和M1.0,磚墻厚度分別為240 mm和360 mm,試件頂部施加豎向荷載分別為0.1 MPa、0.3 MPa和0.6 MPa。試件加載方式如圖4所示,加載時保持豎向荷載不變,按照《建筑抗震試驗規程》(JGJ/T 101-2015)[20]的規定,采用力-位移雙控制方法對頂梁施加水平往復荷載。試件編號方式：墻體厚度-砌筑砂漿強度等級-面層砂漿厚度-豎向壓應力;EW為240 mm墻,SW為360 mm墻;例如,EW-0.4-D20-0.1表示240 mm墻-砌筑砂漿強度等級M0.4-單面加固面層砂漿厚度20 mm-豎向壓應力0.1 MPa。試件面層砂漿強度等級均為M10,面層砂漿厚度為20 mm時不配筋,面層砂漿厚度為40 mm時配φ6@300的鋼筋網片。

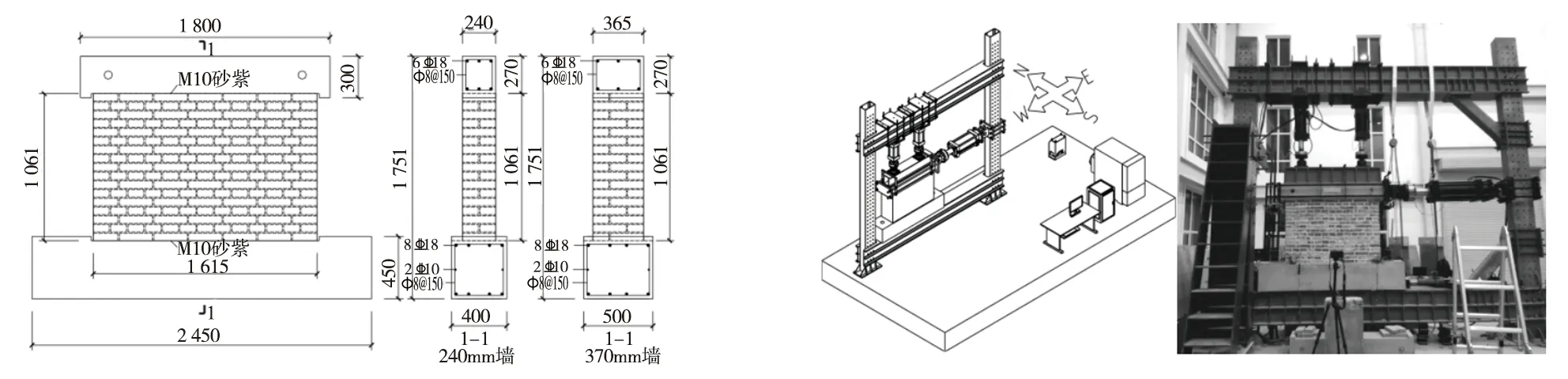
圖3 設計試件幾何模型 圖4 試件加載裝置Fig. 3 Geometry model of designing specimens Fig. 4 Test devices

3.2 試驗現象及破壞機理

各試件試驗現象及典型的破壞模式,如表3和圖5所示。由表3可知：不同豎向壓應力下,未加固墻破壞模式大部分為沿階梯形斜裂縫受剪破壞,而加固墻呈現出沿通縫受剪破壞與沿階梯形斜裂縫受剪破壞兩種模式：(1)當σy/fm≤0.11時,加固墻主要呈現出沿通縫受剪破壞模式,屬于典型的剪摩破壞。該破壞模式發生的條件為,當豎向壓應力較小時,水平荷載使水平灰縫中砂漿產生較大的剪切變形,剪切面出現相對水平滑移,此時由垂直于剪切面的壓應力產生的摩擦力抵抗水平荷載。在試驗中則具體表現為：未配筋面層加固試件的磚墻底部首先出現水平裂縫,隨后砂漿面層底部也出現水平短裂縫,磚墻裂縫與砂漿面層裂縫逐漸擴展貫通,產生相對滑移現象;配筋面層加固試件的磚墻底部首先出現水平貫通縫,而由于配筋面層抗剪能力大于磚墻使兩者變形不一致,導致磚墻底部與面層脫離。這也表明：在較低的豎向壓應力下,配筋砂漿面層并不能充分發揮其抗震能力;(2)當σy/fm>0.11時,加固墻主要呈現出沿階梯形斜裂縫受剪破壞模式,屬典型的主拉應力破壞模式。該模式發生的條件為,當豎向壓應力較大時,加固墻的剪摩強度超過加固墻斜截面的平均主拉應力強度,因斜截面抗主拉應力的強度不足而產生剪壓破壞。在試驗中則具體表現為：加載過程中磚墻先出現少量水平短裂縫,但隨著荷載的繼續增加,水平短裂縫不繼續擴展,而是砂漿面層與磚墻同時產生沿灰縫的階梯形斜裂縫,并持續擴展形成貫通的X型斜裂縫。這也表明：在較高豎向應力作用下,砂漿面層與磚墻協同工作良好,并可較好的發揮其抗震能力。

圖5 試驗中磚墻的典型破壞模式Fig. 5 Failure modes of masonry wall in experiments

表3 試件破壞模式Table 3 Failure modes of test-members

3.3 強度增強系數

規程、規范與試驗強度增強系數如圖6所示。強度增強系數試驗均值為1.12,提高程度不明顯。規程與規范計算的強度增強系數均值分別為1.49和1.23,高于試驗值。20 mm未配筋加固墻：規范增強系數與試驗值基本接近;規程增強系數,在砂漿強度等級M0.4時,高于試驗值。40 mm配筋面層加固墻：規程與規范值均高于試驗增強系數,隨著豎向壓應力的提高,規范的計算值逐漸接近于試驗值。整體上,規范與規程對于未配筋面層加固墻的抗震承載力驗算較為準確,但過高估計了配筋面層加固墻的抗震承載力。

圖6 規程、規范與試驗強度增強系數Fig. 6 Comparison of the coefficients of strength enhancement of GB 50702-2011,JGJ 116-2009 and experiments

3.4 建議公式

據表3試驗現象及破壞模式可知：沿通縫受剪破壞的加固墻的配筋砂漿面層未出現破壞。沿階梯形斜裂縫受剪破壞的加固墻的砂漿面層開裂后,鋼筋并未達到屈服,即鋼筋網片并不能完全發揮作用,宜考慮砂漿和鋼筋網的整體貢獻,而不宜分開考慮。

鋼筋網水泥砂漿面層的貢獻建議按式(12)考慮,[·]內表示砂漿面層的整體貢獻：

(12)

σy/fm≤0.11時,加固墻發生沿通縫受剪破壞,符合剪摩(庫倫)破壞準則,建議采用公式(13)計算加固墻的極限承載力,通過擬合得到,系數a1=0.57,a2=1.2,b1=0.01。

(13)

式中：a1和a2為擬合系數;fv0m為原砌體抗剪強度均值。

σy/fm>0.11時,加固墻發生沿階梯形斜裂縫受剪破壞,符合主拉應力準則,建議采用公式(14)計算加固墻的極限承載力,通過擬合得到系數a1=2.98,b1=0.07

(14)

3.5 極限承載力校核

3.5.1 未加固墻極限承載力校核

式(13)和式(14)的第一項表示未加固墻的極限承載力。規范中未加固墻極限承載力驗算公式可表示為：

FuG=ξNfv0mA

(15)

本文建議公式和規范公式計算值與試驗值見表4。本文建議公式計算值誤差均值為0.12,標準差為0.10。規范公式計算值誤差均值為0.25,標準差為0.13。表明建議公式能較好的反映未加固墻極限承載力。

表4 未加固墻本文建議公式計算值與試驗值對比Table 4 Comparison of test-value and calculated value of unreinforced walls

3.5.2 加固墻極限承載力校核

采用式(13)和式(14)計算的極限承載力見表5,與試驗值之間的誤差均值為0.11,方差為0.10,可以較好的反映砂漿面層單面加固低強度砌體墻的極限承載力。采用式(13)和式(14)校核不同文獻中鋼筋網砂漿面層雙面加固砌體墻試件見表6(文獻[7]豎向荷載為施加于頂梁端部的集中力,本文進行了均布荷載簡化考慮,其他文獻的加載方式與本文一致)。對雙面加固的試件,建議公式的計算值誤差均值為0.15,方差為0.09,能夠較合理的反映雙面加固構件的實際極限承載力。由fv0=0.42fv0m知[18]：式(13)和式(14)第一項乘以0.42可得到未加固墻設計驗算表達式;式(13)和式(14)第二項中用砂漿面層軸心抗壓強度設計值和鋼筋網屈服強度設計值代替相應的均值和標準值可以得到面層強度的設計表達式。因此,砂漿面層加固砌體墻的設計驗算表達式如式(16)。

表5 加固墻建議公式計算值與試驗值對比Table 5 Comparison of test-value and calculated value of reinforced walls

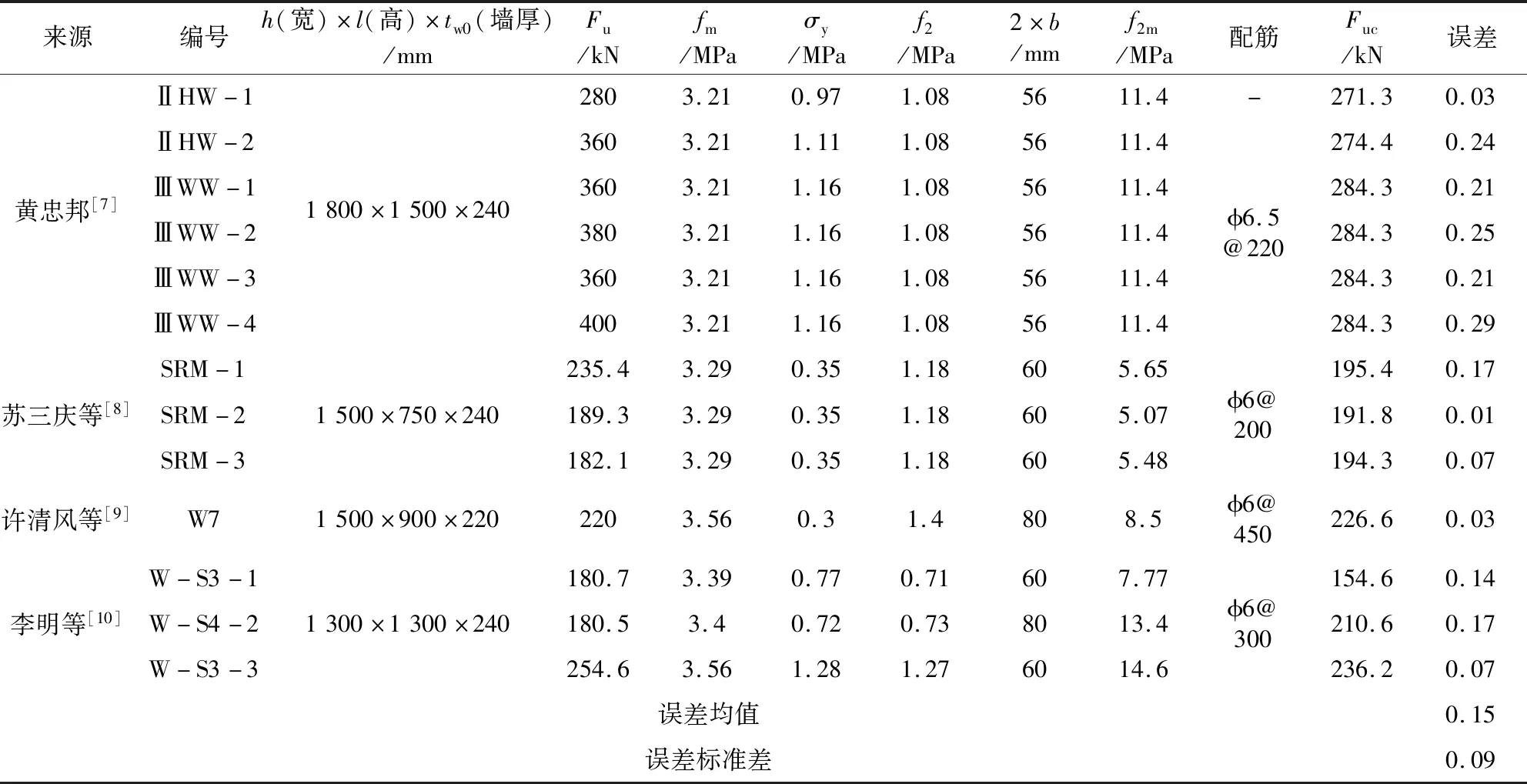
表6 本文建議公式校核雙面加固試件Table 6 Check the double reinforced members by proposed expression

(16)

式中：fv0為砌體抗剪強度設計值;fd為抗壓強度設計值fm=2.22fd[18];σy為重力荷載標準值下的豎向壓應力。

4 基于建議公式的抗震可靠指標

未加固墻功能函數：

(17)

加固墻功能函數：

(18)

未加固墻抗震可靠指標：令式(17)g′before=0,計算地震作用SEhk(相當于原結構所能承受地震作用的上限值),將SEhk帶入式(17),根據表2中變量的分布特征,采用蒙特卡洛方法計算未加固墻的抗震可靠指標,可得未加固墻抗震可靠指標β′before≈2.2。

加固墻抗震可靠指標：將上述SEhk帶入式(18),根據表2中變量的分布特征計算滿足表1條件的加固墻抗震可靠指標見表7。可知：加固墻抗震可靠指標隨砌筑砂漿強度等級提高而降低,隨面層厚度的增加而提高;240 mm加固墻可靠指標高于360 mm加固墻;加固墻的抗震可靠指標為2.5～3.1,與未加固墻相比提高0.3～0.9。

表7 建議公式的抗震可靠指標Table 7 Reliability indices of proposed expression

5 結論

1)《砌體結構加固設計規范》和《建筑抗震加固技術規程》中砂漿面層加固砌體墻驗算表達式的抗震可靠水平有較大不同,兩標準在實際工程應用中容易出現矛盾。

2)未加固墻破壞模式一般為沿階梯形斜裂縫受剪破壞,加固墻在σy/fm≤0.11時,發生沿通縫受剪破壞,σy/fm>0.11時,發生沿階梯形斜裂縫受剪破壞。

3)《砌體結構加固設計規范》和《建筑抗震加固技術規程》對未配筋面層的加固墻的抗震承載力驗算較為準確,但過高估計了配筋面層加固墻的抗震承載力。

4)建議公式的極限承載力驗算值與試驗值吻合良好,可以較為準確的反映未加固墻、水泥砂漿面層單面和雙面加固墻的極限承載力。

5)建議公式驗算的未加固墻抗震可靠指標為2.2,砂漿面層加固后抗震可靠指標為2.5～3.1,采用砂漿面層加固砌體結構可以顯著提高結構的抗震性能。