基于阿基米德螺旋加密重構技術的無人航行器KT 辨識研究

韓璐羽，白佳鈺，于曹陽，連 璉,2

(1.上海交通大學海洋學院，上海 200030；2.上海交通大學海洋工程國家重點實驗室，上海 200240)

0 引言

近年來，無人航行器被廣泛應用于海洋科學與工程任務，建立高精度操縱模型是航行器設計、優化與控制的基礎。目前常用的Abkowitz 整體模型和MMG分離模型中水動力參數較多，相應的辨識系統輸入矩陣維度增加，辨識計算量較大[1]；而Notomo提出的操縱響應方程參數較少、計算簡捷且可直接從約定試驗中獲得，這有利于提高運動控制、性能預測等的實時性，在無人航行器研究領域得到廣泛應用。

精確辨識方程中各水動力系數是優化建模的關鍵一環。傳統系統辨識方法包括最小二乘法(least square,LS)[2–3]、極大似然法(maximum likelihood,ML)[4]、卡爾曼濾波法(Kalman filter,KF)及其拓展[5–6]等，基于現代人工智能技術又發展出了人工神經網絡(artificial neural network,ANN)[7]和支持向量機(support vector machine,SVM)[8]等方法。孫功武等[3]優化最小二乘法，提出了一種基于模糊控制的動態遺忘因子迭代最小二乘(recursive least square,RLS)算法，實現了遺忘因子針對誤差的動態調整，有優越的辨識精度與收斂速度。褚式新等[4]根據辨識原理與前向差分法設計了一種極大似然辨識方法，較傳統卡爾曼濾波算法預報更為精準。秦操[6]采用無跡卡爾曼濾波(unscented Kalman filter,UKF)算法，設計分步辨識，有效提高了辨識精度。以上研究側重于在現有試驗數據的基礎上，改進算法以提高收斂速度以及辨識精度。

但在系統辨識算法已較為成熟的情況下，用于計算的航向數據質量對精度影響可能更為顯著。動態試驗中，航向傳感器的數據采集頻率與精度相互制約[9–10]，不足以支持高精度的模型辨識。當前技術水平限制下，對稀疏數據進行插值重構是高效提高辨識精度的重要途徑。常用的插值方法有拉格朗日插值、分段線性插值、三次樣條插值等，但三者重構的光滑程度不完全符合無人航行器航向隨時間光滑連續變化的實際情境[11 –12]。

阿基米德螺旋(Archimedesspiral, AS)在變量光滑連續變化方面具有較大優勢。現有研究中，AS結構多用于平面天線的設計與實現[13–14]。此外，在對非圓二次曲線與樣條曲線輪廓機械加工時，應用AS擬合離散點，較一系列折線、圓弧等，實現了確保精度前提下的計算量減少[15]。本文嘗試將AS應用于初始航向數據的插值重構，探索該方法在操縱辨識數據預處理方面的更大潛力，對于優化原始稀疏數據以得到更為精準的操縱模型有重要意義。

本文首先引入無人航行器一階線性響應模型，使用采樣頻率不同的數據集進行參數辨識，揭示航向預測精度與采樣頻率的關系；之后，使用AS插值重構數據，改善最小二乘算法在初始采樣數據稀疏時的辨識精度。最后，通過與初始稀疏數據集、基于三次樣條插值的加密集辨識結果對比，證明AS插值方法的優越性。

1 無人航行器操縱運動數學模型

為實現對無人航行器航向的精準預測與控制，需建立其航向角與垂直舵角之間的響應方程。假定前向速度恒定，忽略橫搖、縱傾和浮潛自由度耦合的影響，無人航行器的水平面動力學方程可簡化為[16]：

式中：m為 無人航行器的質量；mii(i=1,2,6)表示其附加質量；Y?和N?為 線性/非線性水動力系數；Y和N為無人航行器驅動執行器產生的側向推力及偏航力矩；Iz表示繞z軸的慣性矩。

假設僅小舵角操縱無人航行器，則式(1)可進一步簡化為：

式(2)經變換，得到：

式中： δ為舵角，rad；T1，T2，T3為時間常數，s，表征無人航行器的應舵性和航向穩定性；K為舵角增益，s?1，也稱旋回性指數。上述K和T參數具體表達為：

式(3)即為日本Notomo教授提出的一般性首搖響應線性方程，通常稱作二階線性KT方程。本文側重于探究響應方程參數辨識過程中由于輸入數據“航向-舵角”稀疏產生的問題及相應優化方法。為此，在操舵不很頻繁的前提下，參數辨識與設計優化階段選取進一步簡化的一階線性KT模型：

也可用航向角 φ(rad)表示為：

式中：

2 響應模型參數辨識及辨識精度判定原理

2.1 基于最小二乘算法的響應模型參數辨識

對一階線性KT 模型進行參數辨識時，首先將式(9)作離散化處理，即用向前差分代替原本微分形式。整理得：

式中： ?t表示航向/舵角傳感器兩次采樣的間隔時長，s；φ(t) 和δ (t) 分別為t時刻無人航行器航向角和舵角。

將式(11)表達為矩陣形式，即可得到最小二乘法的標準辨識模型AX=b。矩陣具體表達為：

輸出矩陣

輸入矩陣

參數矩陣

此參數矩陣X的最小二乘解為：

因此，將操縱試驗中航向/舵角傳感器采集的數據依次代入輸入矩陣和輸出矩陣，即可解得式(9)中一階線性響應模型的K和T參數。

2.2 參數辨識精度的判定

為確定K和T的辨識精度，將式(11)整理得到如下遞推關系式：

代入初始采樣數據集 ?t，t和δ(t)等數據以及辨識所得參數K和T，預測無人航行器航向角φ′(t)。通過與操縱試驗 φ(t)對比，計算各時刻絕對誤差和總均方根誤差作為參數辨識精度的定量判定標準。

3 數據采樣頻率對辨識精度影響的定量分析

3.1 參數辨識輸入矩陣數據采集

Z 形操縱試驗于1943年由Kempt 提出，用于衡量船舶操縱性能，目前被廣泛應用于無人航行器性能分析，是確定參數K和T的標準方法。本文利用文獻[17]中模型數據，以Matlab為平臺，開展15°Z 形全數字仿真試驗。仿真采樣時間間隔為0.1 s，采樣總時長為20 s，所得數據如圖1所示。

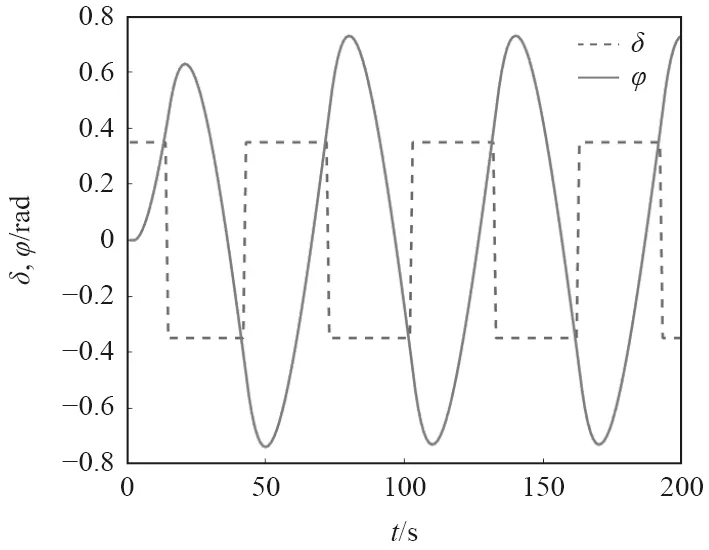
圖1 15° Z形仿真試驗數據Fig.1 Data in 15° zigzag simulation

3.2 輸入矩陣采樣頻率對辨識精度的影響分析

基于圖1中的仿真數據，建立初始采樣數據集S0。從S0中取時間間隔放大為0.5 s和0.2 s 的數據，即分別取t=0.5 s，t=1 s，…，t= 20 s 和t= 0.2 s，t=0.4 s，…，t=20 s 時舵角 δ(t)和航向角φ(t)，構成稀疏數據集S1和S1′。S0、S1和S1′數據如圖2所示。

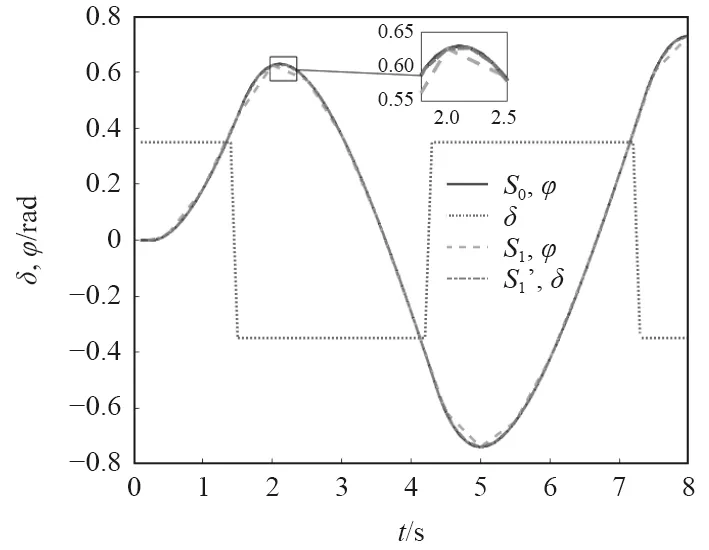
圖2 不同采樣頻率數據集S0、S1和S1′對比圖Fig.2 Comparison of data sets(S0,S1 and S1′)with different acquisition frequencies

對各數據集開展KT參數辨識，辨識結果如表1 所示。

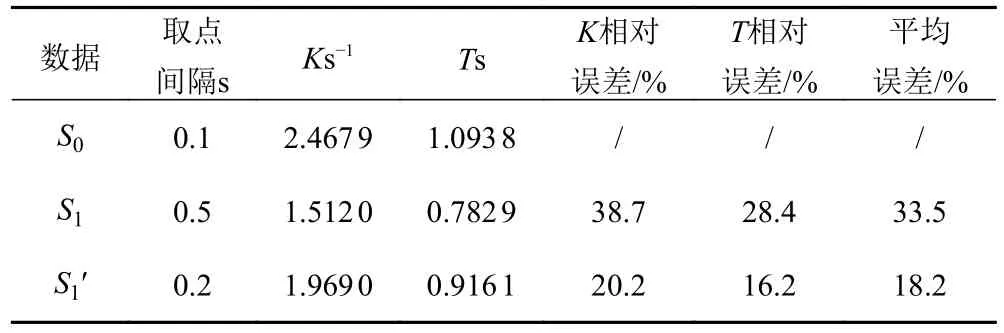
表1 S0，S1和S1′辨識結果對比Tab.1 Comparison of identification results using S0,S1 and S1′

利用上述3個數據集辨識得到的KT數據，輔以式(16)得到無人航行器的航向預測對比結果，如圖3所示。

圖3 S0、S1和S1′所得KT 模型對應的航向預測結果對比Fig.3 Comparison of heading results derived from three data sets(S0, S1 and S1′)

不同密度數據辨識的航向結果均與實測數據存在一定誤差。S0模型預測的絕對誤差在0.02 rad 以內，精度較高，能夠滿足無人航行器響應建模與路徑預測的實際需求。然而，隨著數據采集頻率降低，數據集稀疏程度加深，相應的辨識誤差增大，說明有必要保持一定的數據采集密度。在航向/舵角傳感器數據采集頻率固定的情況下，應用合適的數據插值加密方法對參數辨識輸入矩陣預先進行優化處理，有利于得到高精度無人航行器KT響應模型。

4 基于阿基米德螺旋(AS)重構加密的改進辨識

4.1 稀疏數據集AS插值重構

阿基米德螺旋(AS)的極坐標表達形式如下：

式中：r和 θ分 別為極徑和極角，θ ∈[0,θmax]；k為正常數。

選取采樣間隔為0.5 s的數據集S1進行重構，以t和 φ為基本變量。設第i個數據點為Ai(ti,φi)(i=1,2,3,…)，Ai與Ai+1之 間采用AS幾何連接，記作ASi，參數化表達為：

式中： ρ為依據Ai與Ai+1相對位置關系確定的AS螺旋方向， ρ=1表示螺旋路徑從極坐標的原點(Ai)按順時針方向傳播； ρ=?1即按逆時針方向傳播； σ表示螺旋初始角度。由于需給定螺旋初始方向，插值至少從采集的第2個數據點(A2)開始，由A2與前點A1確定 σ。ρ和σ 的表達式如下：

為盡可能縮小時間維度響應不足對 σ值的影響，設Ai與Ai?1離散化插值所得點中最接近Ai?1者 為B(i?1)ilast(i>2)，將σ計算調整為：

每段AS重構終止于點Ai+1(ti+1,φi+1)，以此為邊界條件，給定常數k和θmax。完成重構的數據集記作S2。

A1,…,A4數據點為例，重構方法示意如圖4所示。

圖4 AS插值重構方法示意圖Fig.4 The schematic diagram of ASinterpolation method

4.2 重構數據集辨識效果對比

為了進一步體現AS重構加密的優越性，除將其模型參數辨識精度與原稀疏數據集S1對比外，還選取S1基于三次樣條插值的加密集S3作為對照。S0，S1，S2和S3參數辨識結果如表2所示，航向預測精度對比分別如圖5和圖6所示。

由表2，圖5和圖6可以看出，重構加密后的數據集S2和S3較原稀疏數據模型辨識效果有明顯改善，KT參數辨識精度顯著提高，其中K的相對誤差縮小至不到1%；基于KT模型的航向角預測結果絕對誤差縮小了一個數量級。此外，AS彌補了三次樣條插值光滑性不足的缺陷，更加符合Z 形操縱試驗中航向角光滑連續變化的實際情景。圖6表明，AS較三次樣條重構加密精度提高了20%，展現了AS的卓越性。圖5和圖6表明，S2，數據集辨識已較為接近S0所得結果，很大程度上減小了傳感器采樣頻率較低時對無人航行器響應模型辨識的影響。

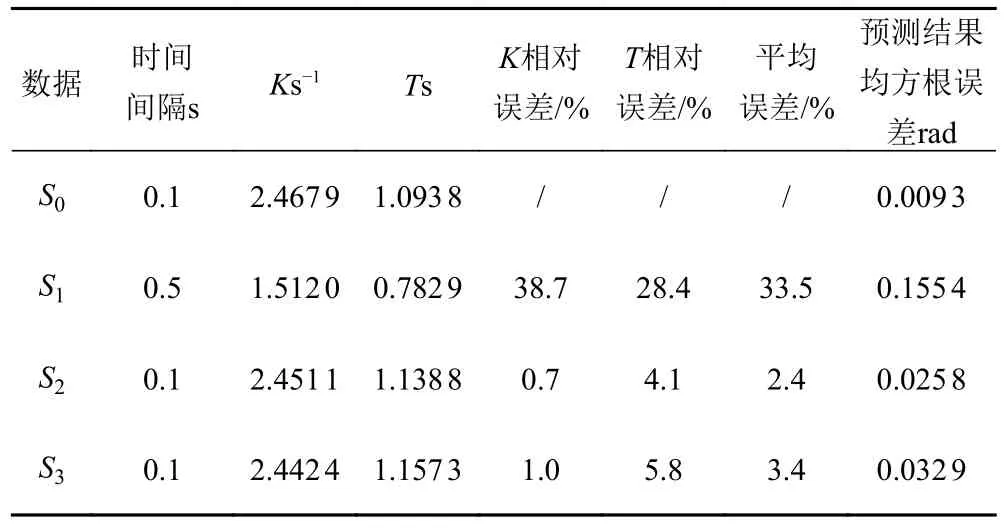
表2 S0，S1，S2和S3辨識結果對比Tab.2 Comparison of identified results of S0,S1,S2 and S3

圖5 S0，S1和S2 所得KT 模型預測結果對比Fig.5 Comparison of heading results derived from three data sets(S0,S1 and S2)

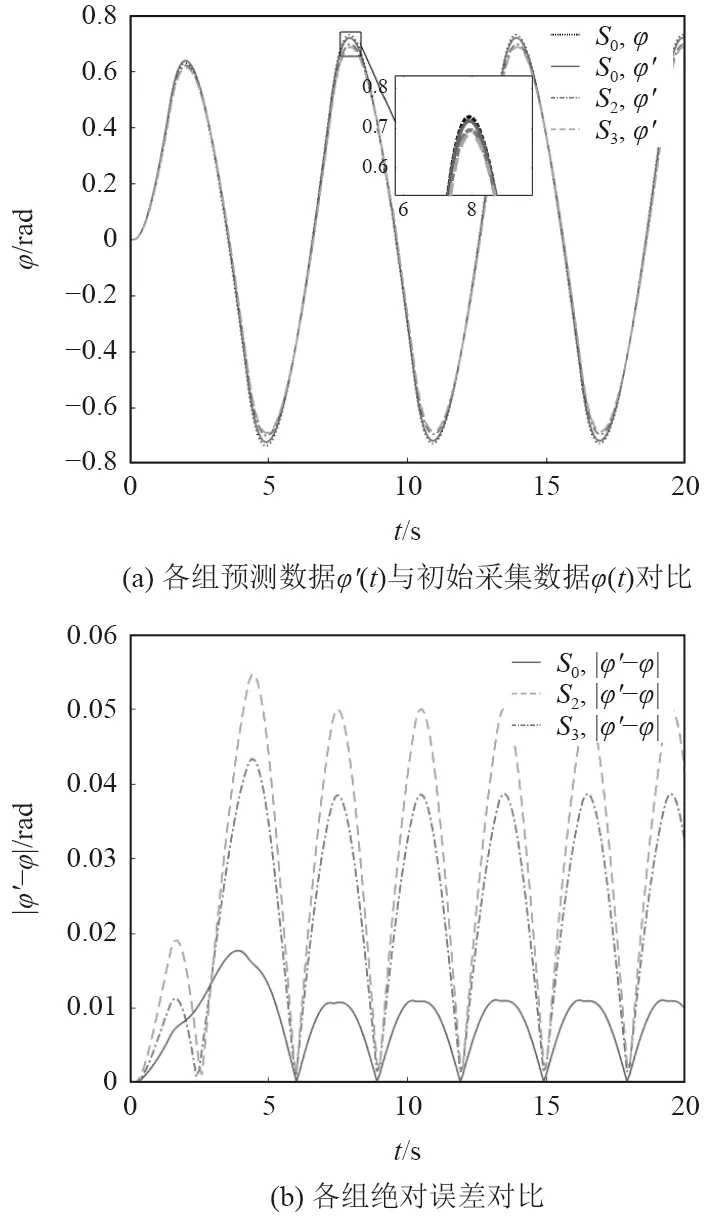
圖6 S0，S2 和S3所得KT 模型預測結果對比Fig. 6 Comparison of heading resultsderived from three data sets(S0,S2 and S3)

5 結語

本文將阿基米德螺旋加密重構算法應用于Z 形操縱試驗數據的插值優化中，并基于重構數據集進行一階線性操縱響應方程的參數辨識。該方法優化了系統辨識算法在稀疏數據集上的表現，并且有效彌補了三次樣條插值光滑程度有限的不足。本文從AS插值優化算法的引入必要性、數據預處理與辨識過程、辨識結果分析與對比等三方面展開研究，得到以下結論：

1）航向數據采集間隔由0.1 s 下降至0.5 s時，KT參數辨識平均誤差增大了33.5%，說明數據采集頻率對參數辨識精度有很大影響。

2）在數據采集頻率受限的情況下，AS加密預處理的數據集與高精度高頻率采樣數據集的參數辨識平均誤差僅相差2.4%。同時依據辨識所得模型預測航向，與實際仿真試驗結果對比，均方根誤差僅為0.0258 rad。表明AS插值優化算法提高稀疏數據集辨識精度的有效性。

3）與基于三次樣條插值算法加密數據的效果對比表明，KT辨識與預測結果誤差均有所下降，驗證了AS在變量光滑連續變化方面具有較大優勢，更適合航向數據優化的實際情境。