基于啟發式算法求解電動汽車碰撞測試排程問題

曹劍雕 陳淮莉

(上海海事大學物流科學與工程研究院 上海 201306)

0 引 言

汽車碰撞測試是汽車生產中的重要一環,其結果往往作為驗證和提升汽車質量的重要考量。消費者也常以此作為購買依據。但是由于碰撞測試的破壞性,使它們的調度既特別重要又受到限制。測試調度過程希望能最大限度地提高車輛的利用率,即安排在同一輛測試車的測試盡可能多以使被毀壞的車輛數量最少,從而增加可用于其他用途或測試的未損壞部件的供應。

在汽車碰撞測試方面,國內研究較少,蓬勃發展的電動汽車也為測試提出了新要求。我國研究此類問題主要還是從整車的結構框架設計要求出發。Sun等[1]研究了新能源汽車發展過程中碰撞的結構性能。為了使新能源汽車不少于傳統燃料汽車乘員保護性能,認為需要關注的加強和優化結構,如復發縱梁、橫梁面前、側板b、閾值和上肢的剛度。Zhang等[2]根據燃油車和電動汽車的區別,對碰撞測試中的汽車電池的安放位置上提出一些建議。

相較于國內,國外研究比較深入,在汽車碰撞測試方面,國內研究較少,國外則比較深入,Garey等[3]證明了機器數量不確定并行機調度屬于NP-Hard問題。而后有學者將碰撞測試調度問題看作是典型的裝箱和并行機器調度問題的混合,Garey等[4]研究將不同尺寸的物品裝入容量有限的箱子中,并確定所需箱子的最小數量。在此基礎上,Elhedhli等[5]則提出了一種具有項目間沖突的裝箱問題。作者給出了該問題的集劃分公式,并提出了一種分枝定價算法,將定價問題作為一個有沖突的背包問題來解決。在碰撞測試調度的背景下,研究人員努力將各種理論方法和技術擴展到實際應用中。Kravchenko等[6]以最大限度地減少機器的數量為目標,同時滿足項目的時間窗要求。使用一種兩階段的方法,首先使用一個時間索引公式來形成項目序列,然后使用啟發式方法把項目分配給每臺機器。Bartels等[7]考慮將建立原型車輛作為決策的一部分,并將問題描述為混合整數規劃(Mixed Integer Programming,MIP)模型。Limtanyakul等[8]提出了一種使用MIP和約束規劃(Constrained Programming)的混合模型安排碰撞測試;他們使用MIP來估計原型車的需求和CP來尋找一個完整可行的時間表,然而,這些削減純粹是組合的,可能會導致緩慢的收斂。馮忠魁等[9]考慮原型樣車可用性,測試優先順序和資源能力等方面的約束,采用約束規劃來求解測試排程問題,Lockledge等[10]應用多階段數學規劃模型來求解原型樣車排程問題。算法上,Lin等[11]將提出的迭代混合遺傳算法與禁忌搜索和蟻群算法做了比較。Liu[12]提出了一種新穎的混合遺傳算法(HGA),用于確定性調度問題,多個不相關的并行機上處理具有任意優先級約束的多個作業。

綜上所述,汽車測試問題上,多以最少數量原型車作為目標函數,在求解策略和算法上有較深入的研究,少有將碰撞測試作為特定研究對象。本文將原型車測試當中的碰撞測試為研究對象,首先使用整數規劃(Integer Programming)模型將碰撞測試聚合成組。將分組的碰撞視為單個測試,而后通過混合貪心策略的啟發式算法將符合測試排程要求的測試安排到原型車,在求解上,分別使用以上方法和約束規劃(Constrained Programming)求解,分析兩種方法的性能。

1 問題描述

1.1 問題概述

電動汽車碰撞測試具有破壞性,通常安排在一般測試之后,某些測試項目損壞程度高,往往一輛車只能安排這一項測試,非其測試時間段則空閑,測試項目中不同測試速度下不同接觸面測試比例較多,可提前設置其兼容性要求,減少車輛的損壞。

傳統原型車車輛測試如圖1所示,圖1中間的橫線表示m輛的原型車,用來測試右邊表示n項測試。圖左表示的是L個樣車變體,這是因為不同的測試要求所造成的,另外是為了了解各個零部件之間最好的搭配和協調。在測試中,為了貼合實際,將原型車的可用、準備時間、可用時間、各項測試的時間因素,測試要求等考慮。建立模型,使得所有的測試都能在截止時間內有序地安排在符合要求的原型車上。

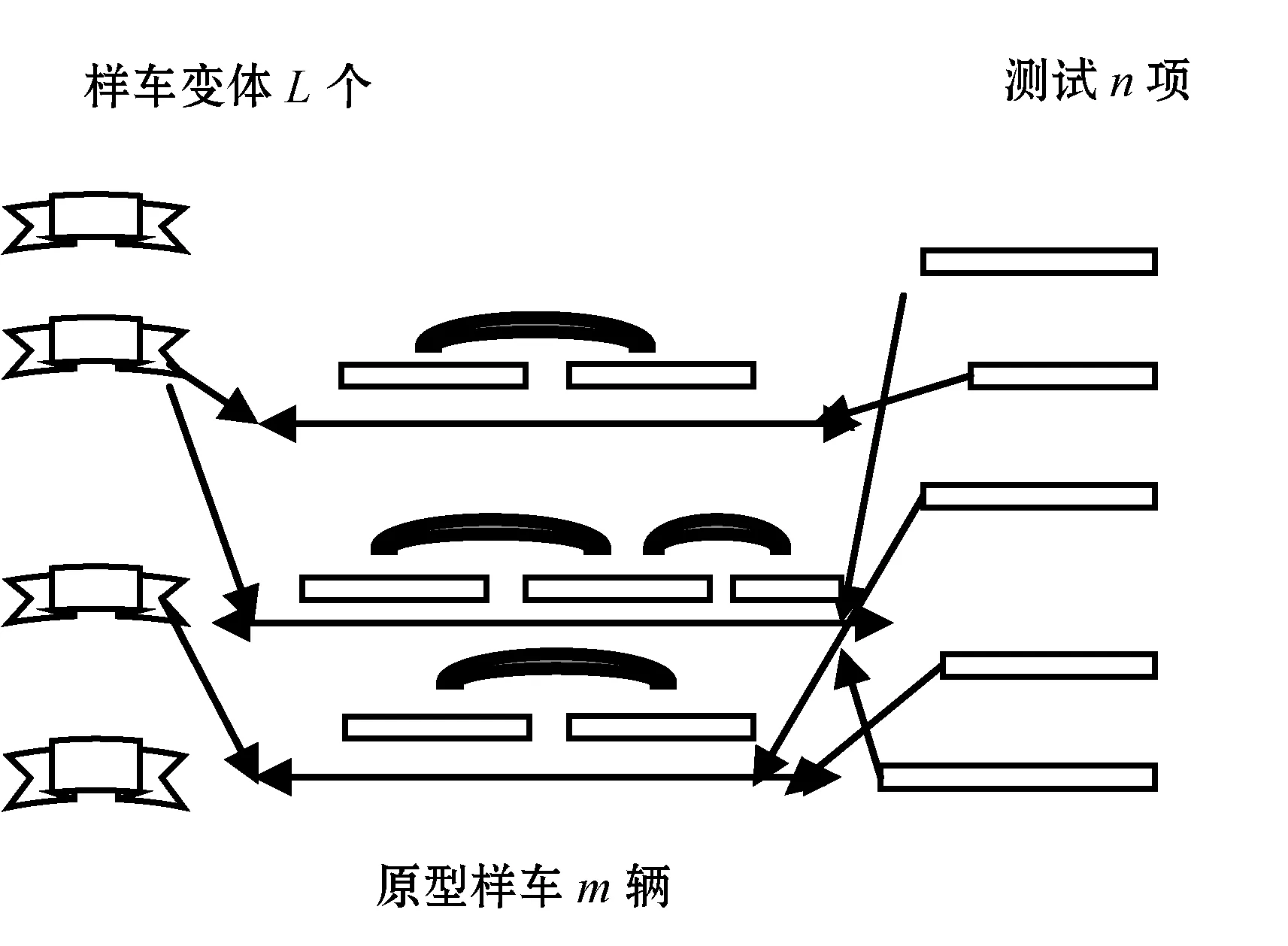
圖1 原型車測試示意圖

本文研究的是新能源汽車中的電動汽車碰撞測試問題。電動汽車普遍采用的是高密度電池模塊來代替燃油。一般來說,汽車在進行各種測試前,無論是燃油車還是電動車,其動力系統應該是最先準備好的,在電動汽車中電池作為一個模塊已經通過了各項安全的要求,但是在整車實驗和現實中電動汽車發生自燃的現象來看,往往是因為在汽車發生碰撞時電池部分受損引起的,因此,在碰撞測試中考慮電池因素很有必要,更符合實際情況。

1.2 問題假設

(1) 測試一旦開始就不能中斷。

(2) 測試的有關時間都是已知的。

(3) 任意時刻任意原型或者變體只能執行一項測試。

(4) 不存在特殊優先關系的約束之間具有同等優先級。

(5) 每一項測試的執行時間具有不確定性,且該測試執行時間與測試順序無關,測試順序都將以最后的優化調度結果給出。

(6) 各項測試之間的轉換時間忽略不計。

(7) 每輛原型車最多匹配一個變體,凡使用一輛原型車或者是變體車都可以視為使用了一輛原型車。

本文主要研究的是新能源汽車中的電動汽車碰撞測試問題。電動汽車與傳統汽車最大的不同就是動力源的不同。電動汽車普遍采用的是高密度電池模塊來代替燃油。這樣的改變也將對碰撞測試提出新的要求。一般來說,汽車在進行各種測試前,無論是燃油車還是電動車,其動力系統應該是最先準備好的,在電動汽車中就是電池作為一個模塊已經通過了各項安全的要求,但是在整車實驗和現實中電動汽車發生自燃的現象來看,往往是因為在汽車發生碰撞時電池部分受損引起的,因此,在整車碰撞測試后,對電池進行一些測試很有意義和很有必要的。本文結合了傳統燃油汽車的碰撞測試經驗與電動汽車的特點進行深入研究。

1.3 聚合測試組整數規劃參數設置及模型

T是碰撞測試項目的集合?t∈T={1,2,…,n}。

I是原型車的集合?i∈I={1,2,…,m}。

ut1.t2,i∈{0,1},取值為1時,表示t1、t2安排在同一輛車,且t1在t2之前測試,取0則為其他情況。

Ei是所有類似于{t1,t2}的集合,并且不符合測試的各項要求,比如:在碰撞測試中,速度高的測試應安排在速度低的測試之前,是因為速度高的測試項目損壞程度可能會影響到后續速度低的測試。

(1)

s.t.

(2)

(3)

ut1,t2,i=0,{t1,t2}∈Ei,i∈I

(4)

ut1,t2,i∈{0,1},t1,t2∈T,i∈I

式(1)是最大數量碰撞測試組;式(2)保證每個測試至少與另外一個安排在同一輛原型車上,同時保證每一對測試最多安排在一輛車;式(3)確保每一輛原型車至多使用一次;式(4)加強兼容性要求。

此模型主要考慮的汽車碰撞測試項目中測試匹配原則較多,如上所述速度高低不同下的碰撞毀壞程度不同,能在一定程度上降低汽車損傷。為了成對匹配的數量最大化,可以迭代多次使更多的單個測試匹配起來,提高求解效率。求出測試匹配集合后需要更新匹配集的各項數據。設測試匹配集tG=(t1,t2,…,tn),ptG、dtG、rtG分別為處理時間、截止時間、投放時間。

rtG∶=dtG-ptG;

fori=n-1:1do

rtG∶=min{dtI,rtG}-ptI

end

2 啟發式算法

啟發式算法的定義為一個基于直觀或經驗構造的算法,在可接受的花費(指計算時間和空間)下給出待解決組合優化問題每一個實例的一個可行解,該可行解與最優解的偏離程度一般不能被預計。電動汽車碰撞測試問題一定程度上也屬于NP-hard 問題,因此采用一種混合貪心策略的啟發式算法,使測試項目在貪心策略下通過啟發式算法安排到原型車上,該算法綜合利用了貪心算法和啟發式算法特點。

2.1 參數設置

T(與1.3節不同)是碰撞測試匹配集tG的集合tG=(t1,t2,…,tn),將單個匹配集視為單個測試項目。

I(與1.3節不同)是已經安排有測試集的原型車的集合?i∈I={1,2,…,m}。

V是樣車變體的集合?v∈V={1,2,…,i}。

M是原型車數目。

N是測試數目。

E是不相容測試集的集合。

pt為測試t的處理時間。

dt為測試t的最后期限。

rt為測試t的投放時間。

ai為第i輛汽車的準備時間。

Ct為測試t的完成時間。

st為測試t的開始時間。

2.2 貪心-啟發式算法

貪心-啟發式算法代碼如算法1所示。

算法1貪心-啟發式算法

%將原型車集合I可用時間降序排列

%將測試項目集合I處理時間降序排

Foreachi∈Ido

Foreacht∈Tdo

Ifi有可用時間 then

Ifi上可用時間滿足測試t,則將t安排在i上;

End

Else

If 排程可滿足問題是可行的,則t安排在上;

End

End

End

從測試集T中移除已經分配的測試;

在i′∈I中找出最少可用時間的,這樣i′上的測試集可以重新分配給i;

Ifi′≠ithen

將所有測試從i重新分配到i′;

在I中調換i和i′的位置;

End

End

該算法的核心思想是盡可能每次都將測試安排到已使用的原型車上,并且符合測試排程要求,從而提高車輛的利用率達到減少使用原型車的數量的目的。

2.3 測試排程滿足模型

當在貪心啟發式算法中將每項新測試安排到原型車時,基于測試之間的兼容性關系和單個測試發布日期和截止日期,必須確定是否存在可行的排序,為了有效地解決這個問題,提出一個全整數規劃模型來求解排程的可滿足性問題。在實際求解CP問題中,往往將約束傳播算法與搜索策略相結合。這樣能夠加快求解的效率。

it1.t2∈{0,1},取值為1時,表示t1、t2安排在同一輛車,且t1在t2之前測試,取0則為其他情況。

Zi.v∈{0,1} ,取值為1時,表示第i輛原型車匹配第v個樣車變體,,取0則為其他情況。

(5)

s.t.

st1+pt2≤st2+M(1-it1.t2)

(t1,t2)∈T*T,t1≠t2

(6)

it1.t2+it2.t1=1 (t1,t2)∈T*T

(7)

it1.t2=0 (t1,t2)∈E

(8)

st≥rtt∈T

(9)

st≥ait∈T,i∈I

(10)

st+pt≤ct≤dtt∈T

(11)

it1.t2∈{0,1}st≥0

式中:T*T表示的是分配在同一輛車上測試的集合。

式(5)為目標函數,為最小數量原型車,將決策變量原型車與變體聯系起來,每使用一輛變體相當于使用一輛原型;式(6)通過使用大M公式對被分配給同一車輛的測試執行成對排序關系;式(7)表示的是安排在同一輛車上進行的測試只執行一次;式(8)加強測試兼容性要求,加快求解時間。式(9)至式(11)確保測試在時間窗口內進行,測試在預定時間內完成。

2.4 約束規劃模型

此模型參數與前文一樣,在此不贅述。

(12)

s.t.

Xi.t≤Zi.vi∈I,t∈T

(13)

(14)

xi.j=xi.ki∈I?j.k∈Tj≠k

(15)

at1+pt1≤at2+M(1-it1.t2)

(t1,t2)∈Tt1≠t2

(16)

it1.t2+it2.t1≤1 (t1,t2)∈Tt1≠t2

(17)

itlows,thighs=1 (tlows,thighs)∈T

(18)

it正,t側=1 (t正,t側)∈T

(19)

pt≥ait∈T,i∈I

(20)

rt+pt≤ct≤dtt∈T

(21)

xi.t∈{0,1},it1.t2∈{0,1},st≥0

式(12)為目標函數,為最小化最晚完工時間;式(13)將決策變量X原型車與變體V聯系起來,每使用一輛變體相當于使用一輛原型;式(14)確保每一項測試集都被分配到車輛進行測試;式(15)表示的是安排在同一輛車上進行的測試集;式(16)和式(17)通過使用大M公式對被分配給同一車輛的測試集執行成對排序關系;式(18)和式(19)表示分配到同一輛汽車的碰撞測試集,低速碰撞集必須安排在高速碰撞集之前,正面碰撞集也必須安排在側面碰撞集之前,這樣直接設定碰撞測試中的某些測試排程順序能夠極大地減少搜索時間,加快可行解的求解時間。式(20)至式(21)確保每次測試在其時間窗口期間執行以及一些變量值域。

3 算例及結論

選取某電動汽車碰撞測試的24項測試項目為例。有關于24項測試項目的相關數據如表1所示。原型樣車準備好的時間都為0,能夠完成每項測試t的測試車輛集合如表2所示。除此之外,測試之間還存在一些要求。

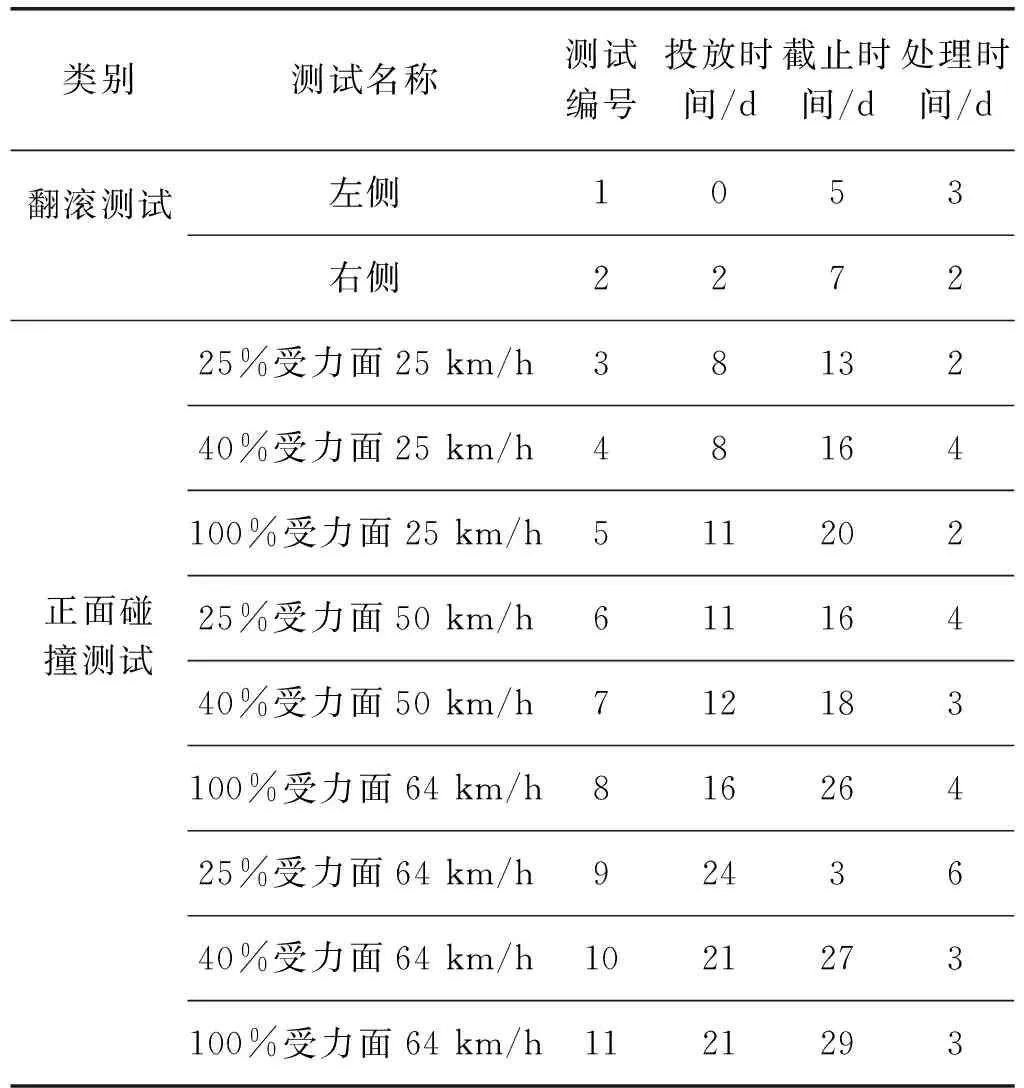
表1 某車型24項碰撞測試數據

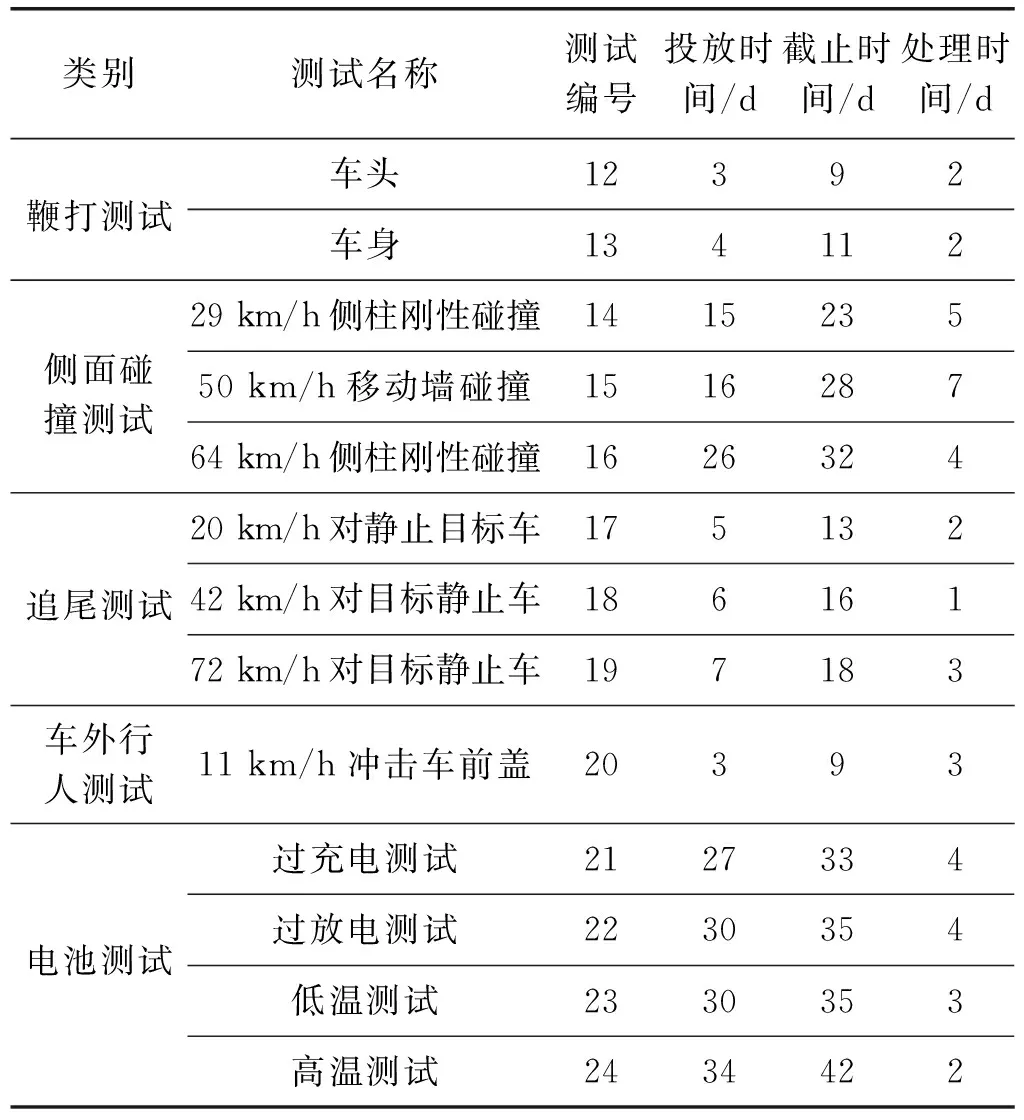
續表1

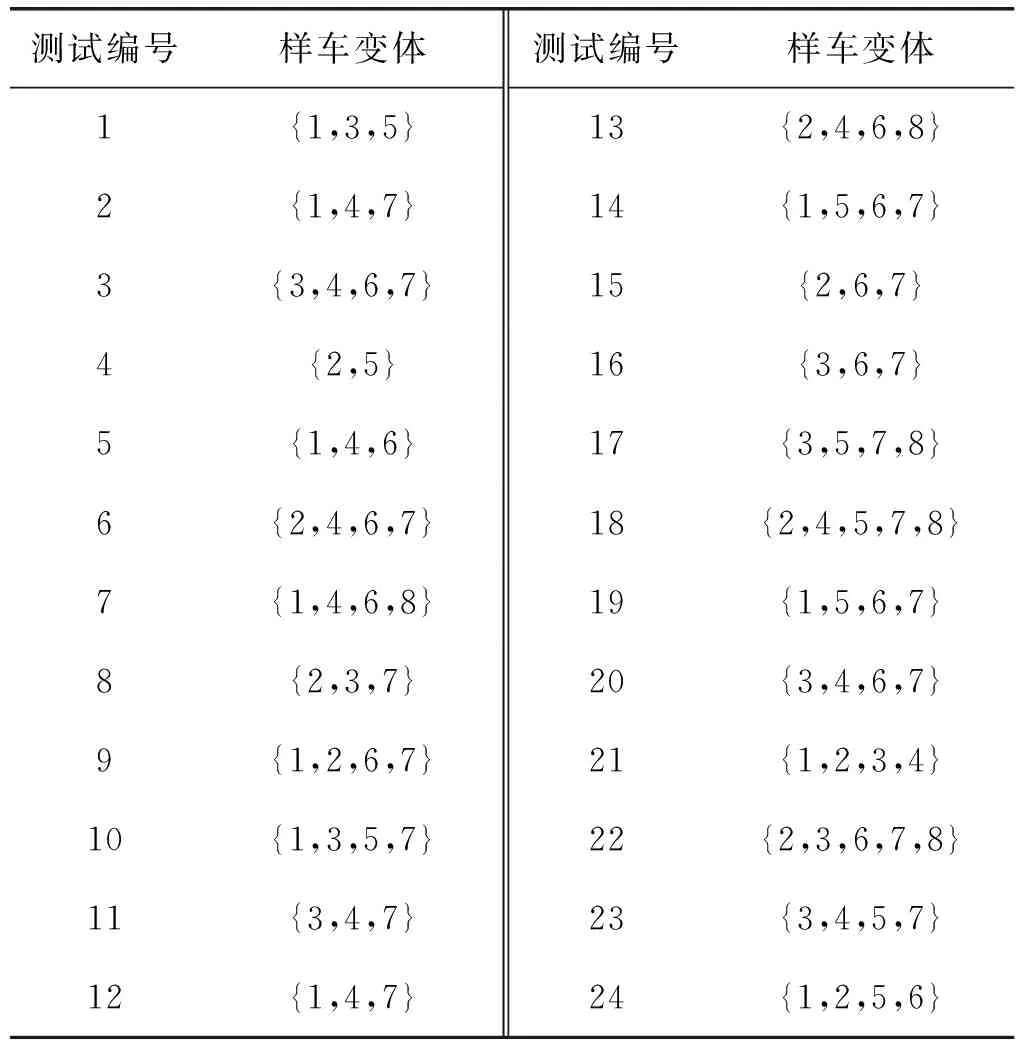
表2 測試與可用樣車變體集合表

1) 測試當中的第8、第9、第10項測試不能放在同一輛車上進行測試。

2) 測試當中的第19、第20項測試必須放在同一輛測試。

3) 測試當中的第4項測試優先于第7項測試,并且必須安排在同一輛車上進行測試。

給定原型車數量6,編號分別為(i1,i2,…,i6)。將這個值作為CP模型中的原型車數量參數,其相應的準備時間為(0,2,4,2,5,3)。表3為樣車與變體之間的關系。

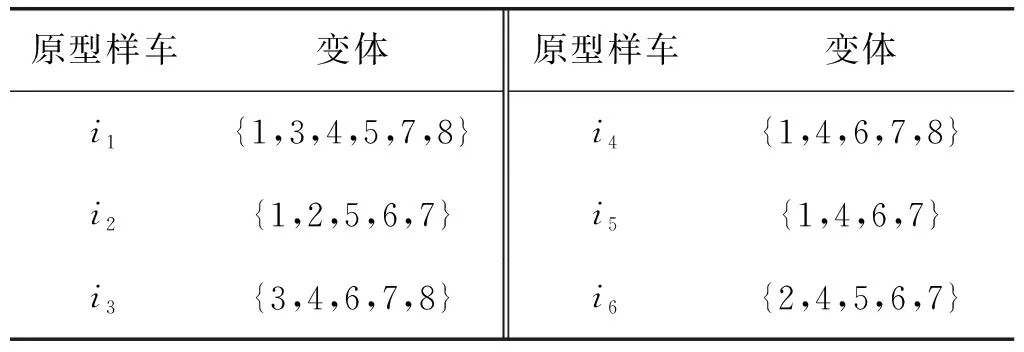
表3 樣車與變體關系

在MATLAB中求解該案例,排程方案如表4所示,分析表4, 24項測試被合理地安排到編號為i1、i2和i6上,與圖2原型車的1、2和3對應。原型車數量為6,減少了一半,完成時間為36 d,達到測試要求。整個測試車輛的平均利用率超過70%,屬于高利用率。之后使用CP約束規劃方法對同問題進行求解,得出的結果在原型車數量和完工時間上相同,證明此算法在電動汽車碰撞測試排程問題上的有效性。

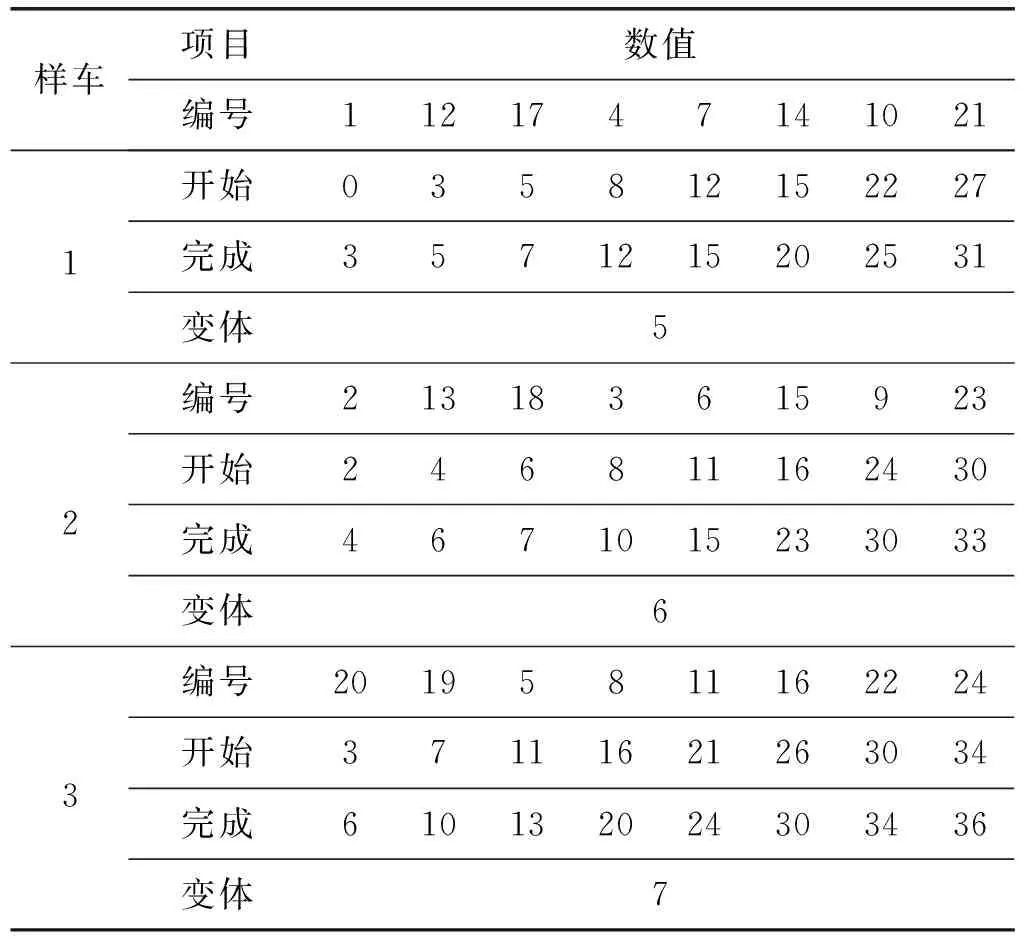
表4 某車型24項碰撞測試排程方案 單位:d

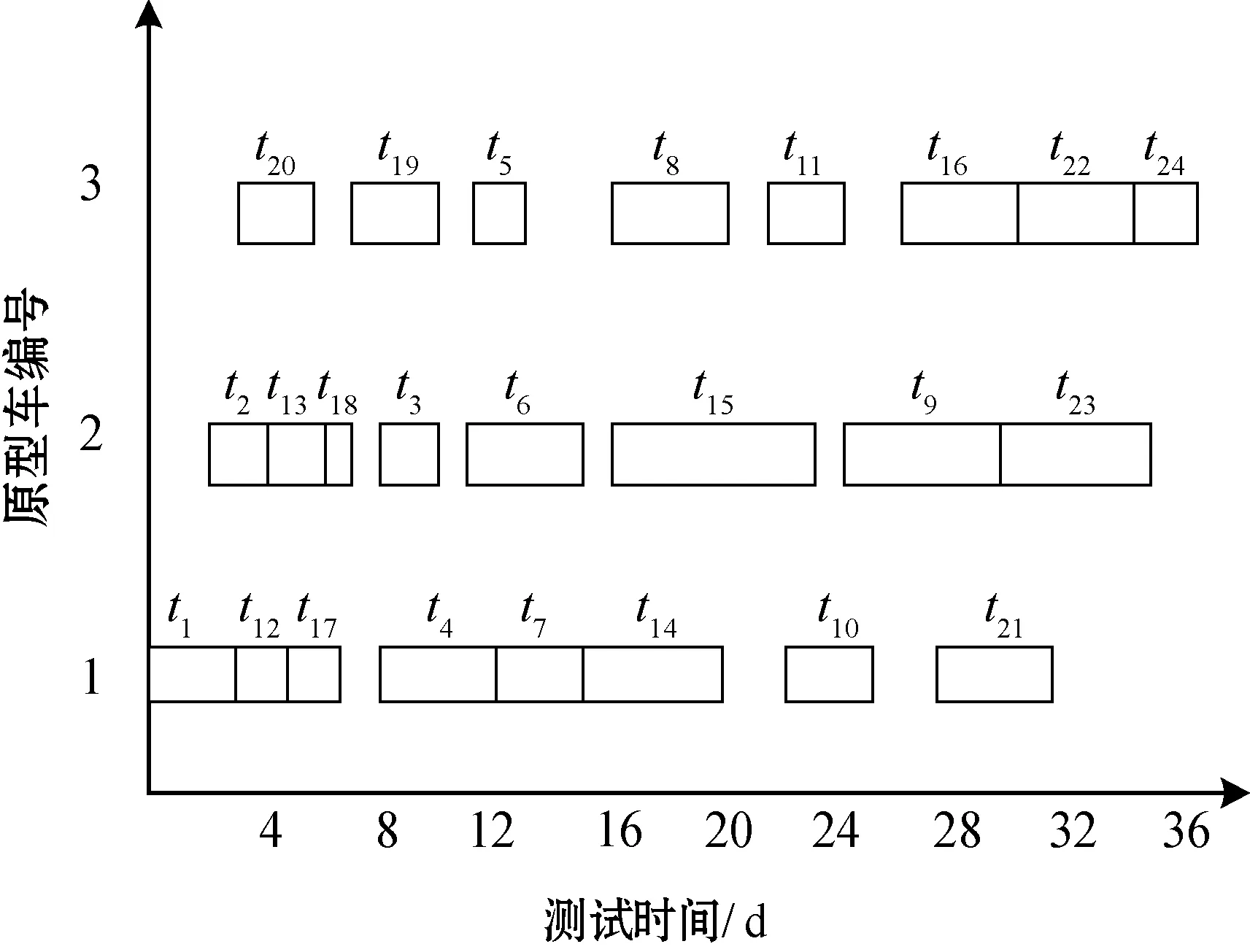
圖2 某車型24項碰撞測試排程甘特圖

現有文獻多以汽車一般測試作為研究對象,碰撞測試是整個汽車測試的重要環節,因其破壞性一般安排在所有測試之后,特選取某新車型20項汽車測試數據如表5所示,在是否使用本文模型算法情況下來分別求解進行分析。

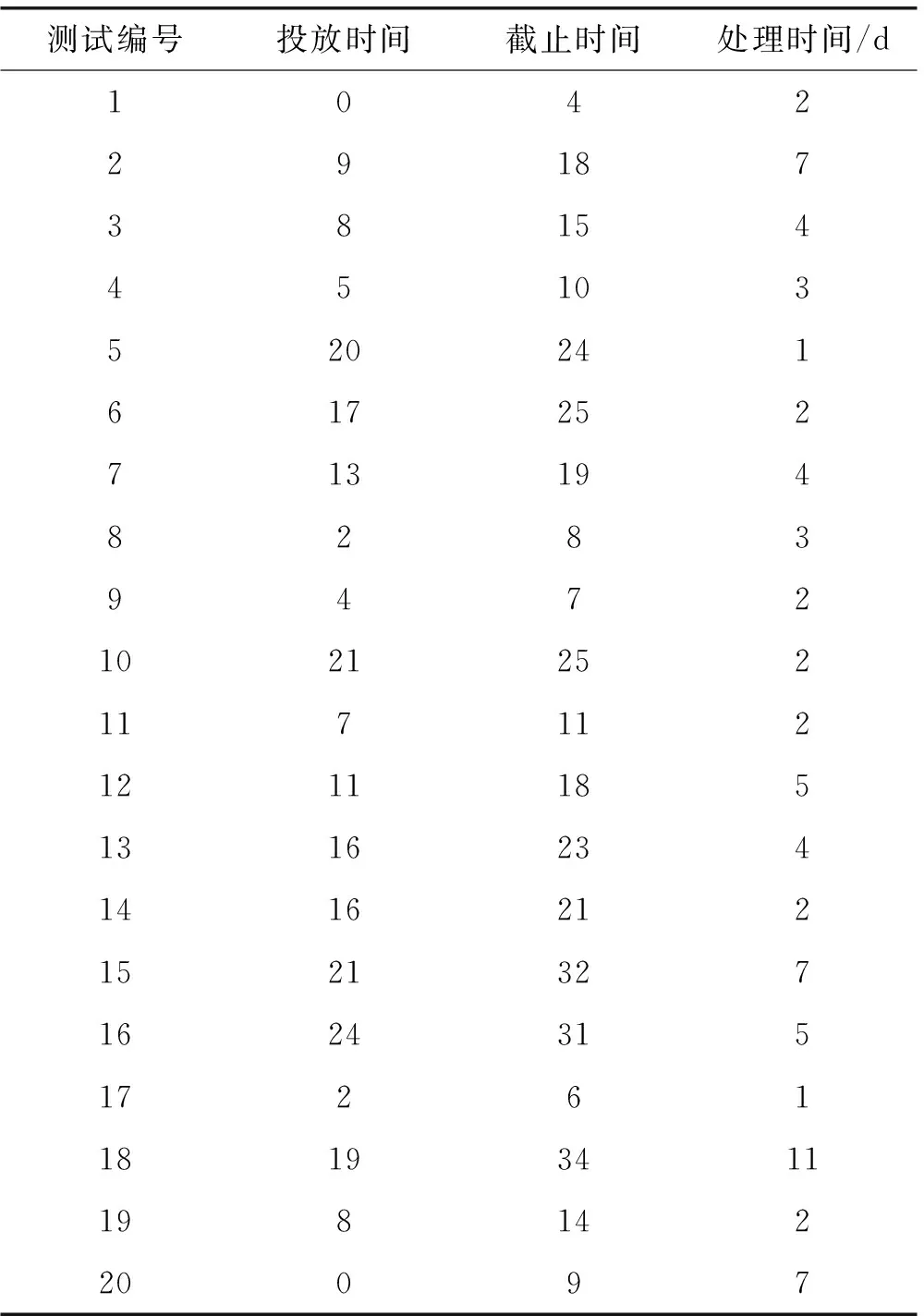
表5 某新型車輛20項測試數據

由表6可知,在使用本文算法和模型情況下,測試時間比沒有使用本文算法和模型下縮短了4 d,在原型車數量上,由5減少到3。

表6 求解結果

以上數據規模較小,為了驗證算法的普遍適用性,擴大數據規模進行分析,數據如表7所示并使用CP求解。

表7 數據集信息及CP求解結果

為了更好地體現算法特點,將是否使用聚合碰撞測試模型進行分別求解,求解結果如表8所示。

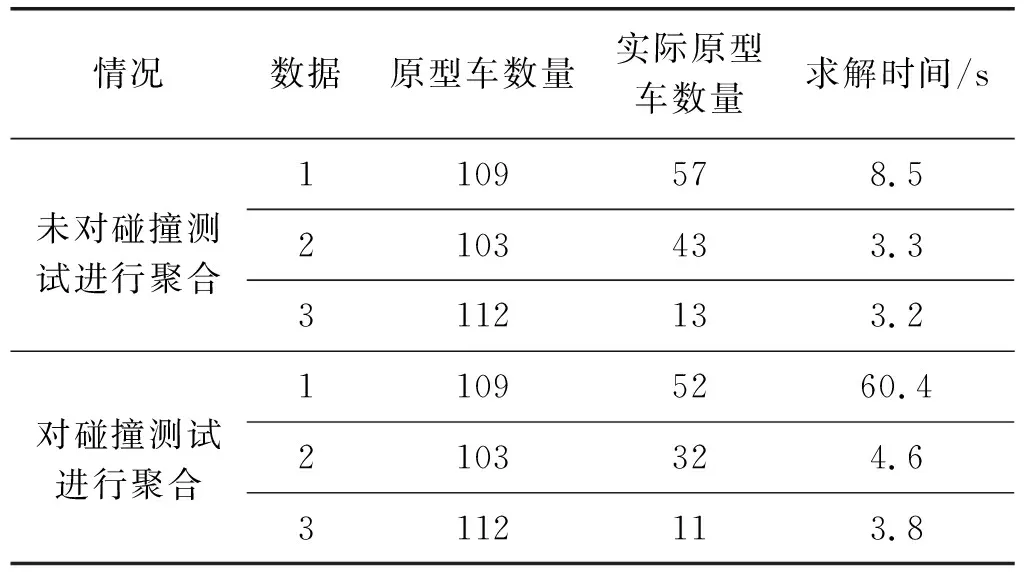
表8 求解結果數據

通過分析表7和表8,可以得出以下幾個結論:(1) CP約束規劃在求解較大規模數據時不能在規定時間內找到可行解,本文算法則都能快速求得可行解;(2) 實際原型車數量使用與碰撞測試數呈正相關關系,符合實際情況,相對原給定原型車數量,實際使用數量有大幅下降;(3) 在兩種可求解到可行方案方法中,未對碰撞測試進行聚合的求解速度是較快的,對碰撞測試進行啟示在實際測試中,啟示應該盡可能完善匹配測試集,減少匹配時間;(4) 對碰撞測試進行聚合的情況下,求解較慢,但減少實際原型車數量較多。

4 結 語

本文主要是研究電動汽車碰撞測試排程問題,考慮電動汽車特點和碰撞測試的具體內容,測試之間的兼容性比較多,在模型和算法設計中進行體現,將單個測試項目聚合成測試集,得到新的測試集數據,而后采用貪心啟發式算法對滿足測試排程要求測試進行排程。通過實例證明本文算法在電動汽車碰撞測試排程問題上的有效性和可行性。對于后續的研究,可進一步優化測試匹配集的細節同時將測試的不確定性情況考慮進來,使模型更加完善。