河流生態系統中兩個相互作用種群的空間模式的形成①

喻鳳斯， 尹甜， 黃啟華

西南大學 數學與統計學院，重慶 400715

大量水生生物(如浮游生物、藻類、溪流昆蟲等)生活在河流、溪流等具有單向水流的生態系統中.為何生物種群在受到從上游向下游單向水流不斷沖刷的情形下能夠生存?這是河流生態理論中一個重要的被稱為“漂移悖論”(driftparadox)的科學問題.為了解釋該科學問題,多位科學工作者建立并研究了一系列包括對流和擴散過程的反應-擴散-對流方程模型和積分-微分方程模型[1-7].這些模型描述了河流種群的時空演變過程,其長期動力學行為(持久性或滅絕)通過多種數學理論和工具被深入研究,例如一致持久性、零解的穩定(不穩定)性、正穩態解的存在性和穩定性、臨界區域長度、行波解和漸進傳播速度等.基于上訴文獻中的單個種群模型,許多研究者建立了兩個相互作用的河流種群模型,著重研究了水流的速度、種群的擴散系數等因素如何影響種群的共存(排斥),例如: 文獻[8-10]研究了兩個競爭種群的模型; 文獻[11]研究了河流生態系統中的捕食-食餌種群的模型.這些模型具有以下一般的形式:

(1)

其中:u(x,t),v(x,t)表示位置在x處、時間在t處兩物種的密度;di(i=1,2)是擴散常數,qi(i=1,2)是對流系數(即水流速度),f(u,v)與g(u,v)為反應函數．

當q1=q2=0時,系統(1)變成經典的兩個相互作用種群的反應-擴散方程模型.反應-擴散方程模型中由擴散導致的常數穩態解的不穩定性稱為Turing不穩定性．

本節的主要目的是研究反應-擴散-對流模型(1)中的單向水流(即對流項)對斑圖動力學的影響(q1=q2=q).為此,我們考慮如下長度為L的河流中兩個相互作用種群的動力學模型:

(2)

其中的Neuman邊界條件表示河流上游有隨著河流自然流入的種群,河流下游隨著時間流逝有被河水帶走的種群．

1 q=0時的Turing不穩定

本節討論沒有水流的影響,及q=0的情形下,系統(2)的Turing不穩定性．

假設(u*,v*)是系統(2)的常數穩態解,將系統(2)在(u*,v*)處線性化,令φ=u-u*,φ=v-v*,則有

(3)

其中f1=fu(u*,v*),f2=fv(u*,v*),g1=gu(u*,v*),g2=gv(u*,v*).用矩陣表示為

Ψt=DΔΨ-QΨ+JΨ

(4)

其中

在一維Neuman邊界條件情形下,系統(4)解的形式為

(5)

(6)

其中

(7)

(8)

在(5)式中ω=ω(k)是決定穩態(u*,v*)穩定性的特征值.對于k=0,(6)式的兩個根滿足

(9)

假設

f1+g2<0,f1g2-f2g1>0

(10)

這意味著穩態(u*,v*)在沒有空間作用的情況下是線性穩定的.現在對于k>0,(6)式的兩個根滿足

(11)

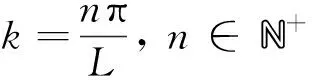
d1g2+d2f1>0

(12)

和

(d1g2+d2f1)2-4d1d2|J|>0

(13)

(14)

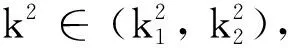
(15)

事實上不等式(15)是不等式(13)的充分條件.通過上面討論得出如下定理．

定理1假設(10),(12),(15)式同時成立的情況下,系統(2)的空間齊次穩態解(u*,v*)會發生Turing不穩定．

2 水流(q>0)對Turing不穩定的影響

接下來考慮在發生Turing不穩定后,加入對流的情況,即系統(2)中q>0．

這時系統(4)解的形式變為

同上討論,(6)式變成:

(16)

其中

Mk的跡和行列式值為:

(17)

aq4+bq2+c=0

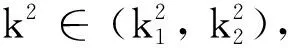
(18)

3 一個捕食-食餌模型的斑圖動力學

標準的Lotka-Volterra捕食-食餌模型假設單位捕食率只依賴于食餌的數量.但在大多數情況下,特別是當捕食者需要花更多時間去尋找食物時,更適合的捕食-食餌系統應建立在所謂的比例依賴性理論上[12].也就是說,單位捕食者增長率應該是食餌與捕食者比值的函數.文獻[13-14]討論了擴散驅動捕食-食餌模型產生空間結構的一些條件.近年來一些研究者研究了比例依賴(即反應項具有收獲率)的捕食-食餌模型[15-16].我們考慮生活在河流生態系統中的捕食和食餌種群的相互作用,研究以下具有捕食者收獲率的反應-擴散-對流比例依賴捕食-食餌模型的時空模型

(19)

其中:u(x,t),u(v,t)分別代表食餌與捕食者的密度,r表示食餌的內在增長率,K代表環境容納量,c代表捕獲率,c1代表轉化系數,m代表半捕獲飽和常數,e代表捕食者死亡率,h代表收獲率.為了方便,對系統(19)進行無量綱化:

仍記變量為u,v,x,t,q,則系統(19)可以寫成

(20)

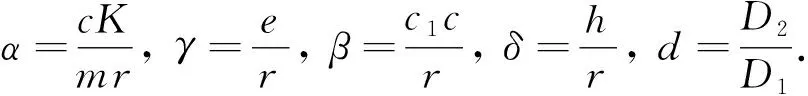
系統(20)對應的常微分系統為

(21)

模型(21)在E*的Jacobian矩陣為

其中:

對應的特征多項式為

P(λ)=λ2-(f1+g2)λ+f1g2-f2g1

對于Jacobian矩陣J(u*,v*)有如下結論．

引理11) 如果(H1)成立,則f1g2-f2g1>0．

2) 如果

(H2)αβ2+β(γ+δ)2<α(γ+δ)2+(γ+δ+1)β2

成立,則f1+g2<0．

3) 如果

(H3)αβ2+β(γ+δ)2>α(γ+δ)2+(γ+δ+1)β2

成立,則f1+g2>0．

通過對Jacobian矩陣J的討論,可得出如下結論．

定理3假設(H1)成立.如果(H2)成立,系統(21)的唯一正平衡點E*是局部漸進穩定的; 但如果(H3)成立,系統(21)的唯一正平衡點E*是不穩定的．

系統(21)正平衡點E*也是系統(20)的空間齊次穩態解.由定理1知,發生Turing不穩定當且僅當

(22)

下面利用Matlab對上訴模型進行數值模擬,以此來驗證以上理論分析的結果．

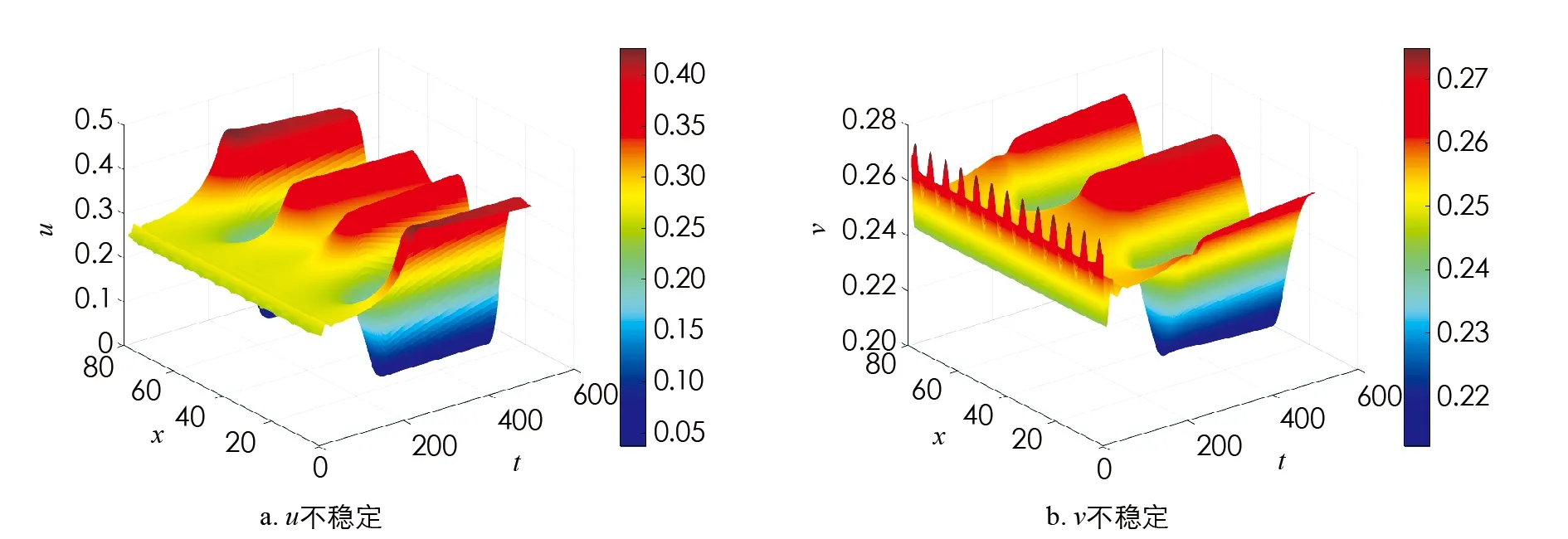
圖2 模型(20)正常數穩態解的Turing不穩定性

圖3 加入q后模型(20)正常數穩態解的Turing不穩定性

圖4 模型(20)重新穩定后的正常數穩態解

4 討論

我們利用反應―擴散―對流方程來描述河流生態系統中的捕食者與食餌的相互作用,研究了在河流長度一定的條件下發生Turing不穩定性的一些必要條件,還研究了對流項對Turing不穩定的影響.發現存在一個對流系數臨界值,當對流系數大于臨界值時會使發生Turing不穩定的常數平衡解重新穩定,但當對流系數小于臨界值時,加入對流項對Turing不穩定性不產生影響.但本文研究的情況比較特殊,本文中的邊界條件是一維Neuman邊界條件,還假設了對流項系數相等.如果對流項系數不等,那么河流長度無限長等情況都有待進一步研究．