含相關(guān)色噪聲和周期方波信號的雙穩(wěn)系統(tǒng)的隨機共振

曾小玲 任芮彬 鄧科

摘 要 ???：本文研究了含相關(guān)色噪聲和周期方波信號的雙穩(wěn)系統(tǒng)的隨機共振（SR）.在絕熱極限條件下，本文利用統(tǒng)一色噪聲逼近（UCNA）法將原系統(tǒng)轉(zhuǎn)化為相關(guān)高斯白噪聲驅(qū)動的新雙穩(wěn)系統(tǒng)，給出其Fokker-Planck方程后基于雙態(tài)理論推導(dǎo)了系統(tǒng)信噪比（SNR）的表達式.本文分析了勢參數(shù)、噪聲參數(shù)及外力參數(shù)對信噪比的影響，發(fā)現(xiàn)對所有參數(shù)隨機共振均出現(xiàn). 本研究可望為實際應(yīng)用提供理論基礎(chǔ).

關(guān)鍵詞 ：隨機共振； 相關(guān)色噪聲； 周期方波信號； 雙穩(wěn)系統(tǒng)

中圖分類號 ：O29 文獻標(biāo)識碼 ：A DOI ： ?10.19907/j.0490-6756.2023.041003

Stochastic resonance in a bistable system with correlated ?colored noises and periodic square wave signal

ZENG Xiao-Ling ?1， REN Rui-Bin ?2， ?DENG Ke ?1

（1. School of Mathematics， Sichuan University， Chengdu 610064， China；

2. College of Mathematics， Southwest Jiaotong University， Chengdu 611756， China）

Stochastic resonance （SR） in a bistable system with correlated colored noises and periodic square wave signal is explored. Given the adiabatic limit condition， the original system is transformed into a new bistable system driven by correlated white Gaussian noises by using the unified colored noise approximation （UCNA） method. Then the Fokker-Planck equation is given for the new system and exact expression for the signal-to-noise ratio （SNR） is deduced by virtue of the two-state theory. Finally， dependence of SNR on the system parameters， including the potenial paramaters， the noise parameters and the external force parameters， is analized. It is shown that SR appears for all parameters. The obtained results are expected to provide a theoretical basis for practical applications.

SR; Correlated colored noises; Periodic square wave signal; Bistable system

1 引 言

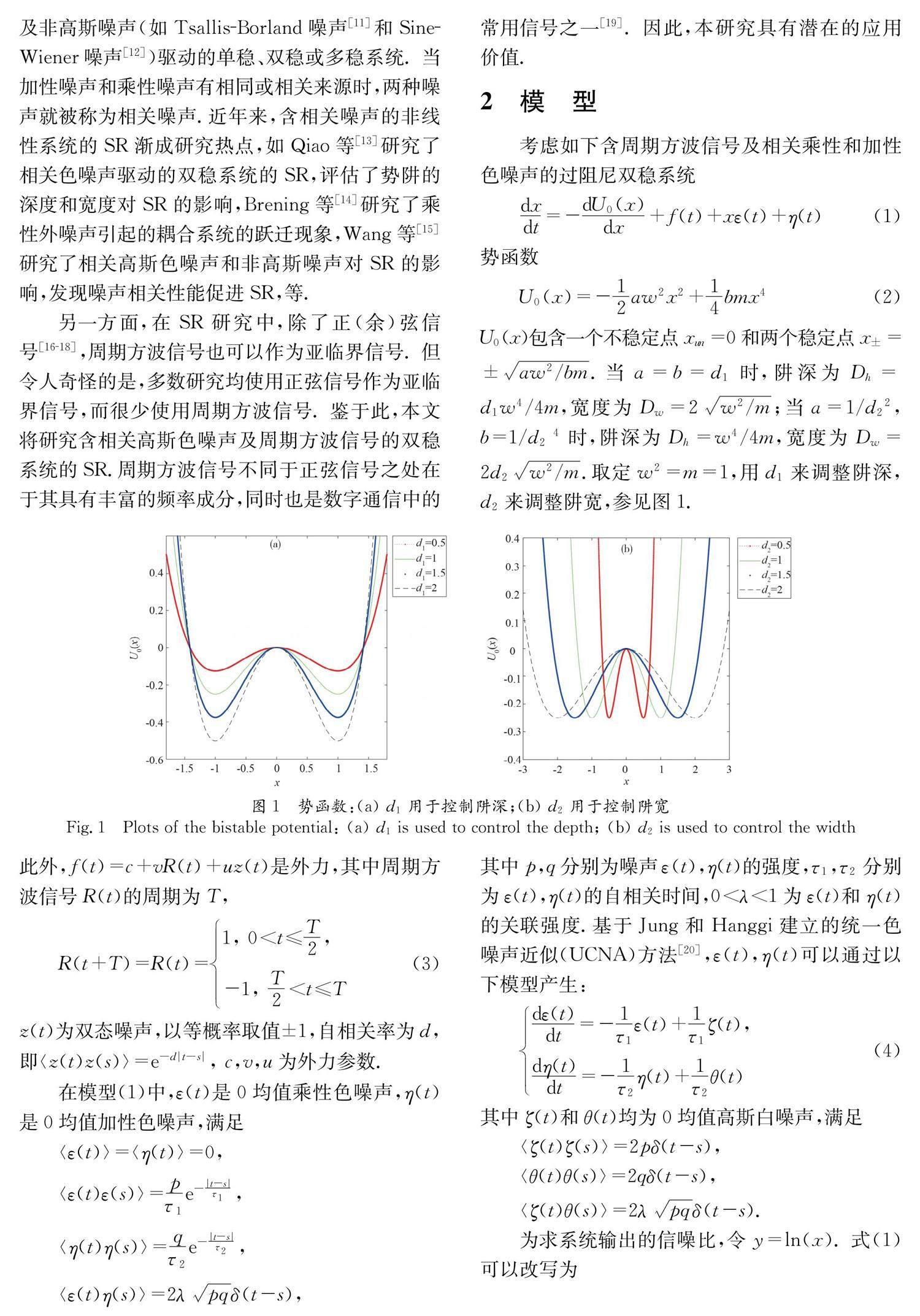
作為噪聲起建設(shè)性作用的例子，經(jīng)典隨機共振（Stochastic Resonance，SR）主要研究噪聲對弱信號（亞臨界信號）的放大作用 ?［1， 2］. 隨后，SR泛指與系統(tǒng)相關(guān)的量化指標(biāo)， 如信噪比（Signal-to-Noise Ratio， SNR），輸出增益（Output Gain， OG）等對系統(tǒng)參數(shù)的非單調(diào)鐘形依賴. SR在物理、生物、化學(xué)及工程等領(lǐng)域均有應(yīng)用， 相關(guān)研究已有很多 ?［3-8］.

最初，SR研究多考慮高斯白噪聲（White Gaussian Noise， WGN）驅(qū)動的單穩(wěn)、雙穩(wěn)或多穩(wěn)系統(tǒng). 然而，鑒于高斯白噪聲在自然界中并非真實存在，近年的研究逐漸轉(zhuǎn)向高斯色 噪聲（如Ornstein-Uhlenbeck噪聲 ?［9］和Mittag-Leffler噪聲 ?［10］） 以及非高斯噪聲（如Tsallis-Borland噪聲 ?［11］和Sine-Wiener噪聲 ?［12］）驅(qū)動的單穩(wěn)、雙穩(wěn)或多穩(wěn)系統(tǒng). 當(dāng)加性噪聲和乘性噪聲有相同或相關(guān)來源時，兩種噪聲就被稱為相關(guān)噪聲.近年來，含相關(guān)噪聲的非線性系統(tǒng)的SR漸成研究熱點，如Qiao等 ?［13］研究了相關(guān)色噪聲驅(qū)動的雙穩(wěn)系統(tǒng)的SR，評估了勢阱的深度和寬度對SR的影響，Brening等 ?［14］研究了乘性外噪聲引起的耦合系統(tǒng)的躍遷現(xiàn)象，Wang等 ?［15］研究了相關(guān)高斯色噪聲和非……