適用于強(qiáng)化學(xué)習(xí)慣性環(huán)境的分?jǐn)?shù)階改進(jìn)OU噪聲

王濤 張衛(wèi)華 蒲亦非

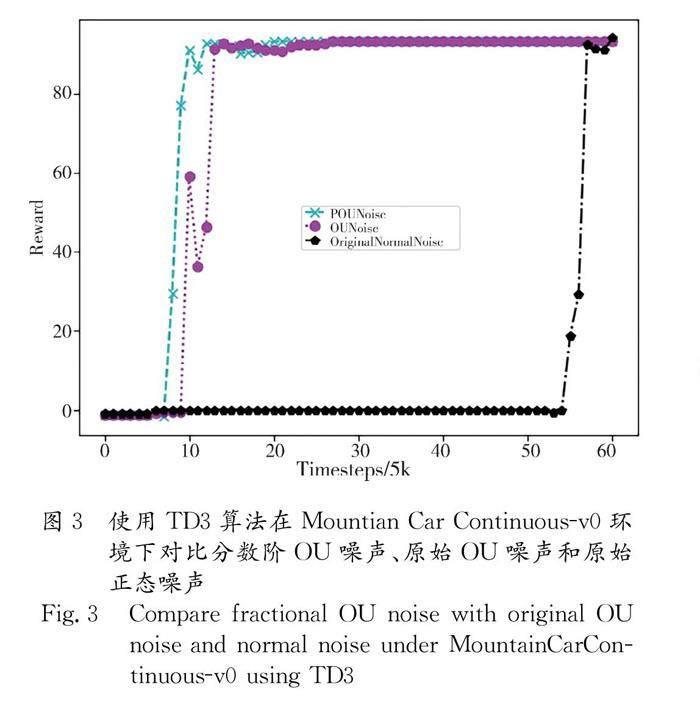
本文將DDPG算法中使用的Ornstein-Uhlenbeck （OU） 噪聲整數(shù)階微分模型推廣為分?jǐn)?shù)階OU噪聲模型，使得噪聲的產(chǎn)生不僅和前一步的噪聲有關(guān)而且和前K步產(chǎn)生的噪聲都有關(guān)聯(lián).通過(guò)在gym慣性環(huán)境下對(duì)比基于分?jǐn)?shù)階OU噪聲的DDPG和TD3算法和原始的DDPG和TD3算法，我們發(fā)現(xiàn)基于分?jǐn)?shù)階微積分的OU噪聲相比于原始的OU噪聲能在更大范圍內(nèi)震蕩，使用分?jǐn)?shù)階OU噪聲的算法在慣性環(huán)境下具有更好的探索能力，收斂得更快.

DDPG算法; TD3算法; 分?jǐn)?shù)階微積分; OU噪聲; 強(qiáng)化學(xué)習(xí)

TP39A2023.022001

收稿日期： 2022-03-26

基金項(xiàng)目： 四川省科技計(jì)劃（2022YFQ0047）

作者簡(jiǎn)介： 王濤（1997-）， 男，? 碩士研究生， 四川資陽(yáng)人， 研究方向?yàn)榉謹(jǐn)?shù)階微積分與強(qiáng)化學(xué)習(xí). E-mail： 2647877536@qq.com

通訊作者： 張衛(wèi)華. E-mail： zhangweihua@scu.edu.cn

An improved Ornstein-Uhlenbeck exploration noise based on fractional order calculus for reinforcement learning environments with momentum

WANG Tao， ZHANG Wei-Hua， PU Yi-Fei

（College of Computer Science， Sichuan University， Chengdu 610065， China）

In this paper， the integer-order Ornstein-Uhlenbeck （OU） noise model used in the deep deterministic policy gradient （DDPG） algorithm is extended to the fractional-order OU noise model， and the generated noise is not only related to the noise of the previous step but also related to the noise generated in the previous K steps in the proposed model.The DDPG algorithm and twin delayed deep deterministic（TD3） algorithm using the fractional-order OU noise model were compared with the original DDPG algorithm and TD3 algorithm in the gym inertial environment. We found that， compared with the original OU noise， the fractional-order OU noise can oscillate in a wider range， and the algorithm using the fractional-order OU noise had better exploration ability and faster convergence in inertial environment.

Deep deterministic policy gradient； Twin delayed deep deterministic； Fractional calculus； Ornstein-Uhlenbeck process； Reinforcement learning

1 引 言

深度Q網(wǎng)絡(luò)（DQN）［1］的提出開(kāi)創(chuàng)了深度學(xué)習(xí)和強(qiáng)化學(xué)習(xí)結(jié)合的先例，DQN算法直接使用了深度神經(jīng)網(wǎng)絡(luò)來(lái)擬合強(qiáng)化學(xué)習(xí)中的Q（s，a） 函數(shù)，并根據(jù)貪心策略選擇下一步需要執(zhí)行的動(dòng)作，這一工作使得算法在Atari游戲上達(dá)到了近似人類玩家的水平.

基于DQN的工作，后續(xù)還有人還提出了DDQN［2］，Dueling DQN［3］，Rainbow DQN［4］等工作，這些工作極大地改進(jìn)了基于值函數(shù)估計(jì)類算法的效果.不過(guò)，這些工作的動(dòng)作空間都是離散的，智能體每次只能選擇有限的幾個(gè)動(dòng)作.然而，在實(shí)際的應(yīng)用場(chǎng)景下，更多的是需要強(qiáng)化學(xué)習(xí)算法處理連續(xù)控制任務(wù).比如無(wú)人機(jī)追逃控制［5］，飛行器高度控制［6］，機(jī)械臂軌跡規(guī)劃［7，8］，無(wú)人機(jī)航跡規(guī)劃［9］等.

對(duì)于連續(xù)控制任務(wù)則無(wú)法直接使用DQN系列的算法，研究人員參考DQN系列算法值函數(shù)估計(jì)的思想，提出了DDPG算法［10］，在……