可視化劈尖干涉法測金屬絲楊氏模量

奉勇輝 宋蕊 李澤昕 張安鑫 李延標 白忠

摘 要 本文利用劈尖干涉法測量微小長度量，對楊氏模量測定儀進行改進，借助CCD視像系統增加儀器操作和讀數的穩定性、精確性。本文的測量方法設計合理，減小了塑性形變和形變的遲滯特性帶來的影響。通過計算結果的誤差分析可知，本文的實驗設計能精確地計算出金屬絲的楊氏模量。該實驗原理清晰，裝置簡單易懂，操作方便，能滿足對材料楊氏模量研究，同時為微小長度量的測量提供了新的思路。本次實驗設計也是對課堂教學的鞏固與拓展，在實驗教學案例中具有很好的推廣價值。

關鍵詞 楊氏模量;劈尖干涉;微小量測量

在外力作用下，受力固體材料發生形變，彈性模量是描述固體材料抵抗形變能力的物理量。各向同性材料的彈性模量包括拉壓彈性模量E、剪切彈性模量G、體積彈性模量K 、泊松比μ 以及拉梅彈性常數λ 等[1]。為了表征材料抵抗縱向弾性形變能力的大小，英國物理學家托馬斯· 楊（Thomas Young，1773—1829）提出：在彈性限度內，材料所受的應力與發生的應變之比是一個常數，因此縱向弾性模量（正應力與線應變之比）也被稱為楊氏模量[2]。楊氏模量越大，表示材料越不容易發生形變。楊氏模量只與材料的固有特性有關，是選定材料力學性能的關鍵依據。特別在軍事應用中如渡河架橋、防彈破甲，精確測量材料的楊氏模量就顯得尤為重要。因此，楊氏模量的測量實驗在當前軍事院校的大學物理實驗課程中的重要性是不言而喻的。同時它在培養學生掌握材料特性和測量理論、鍛煉實踐動手能力等方面具有非常重要的作用。

目前，楊氏模量的測量方法通常分為以下4種：靜態拉伸法、動態共振法、梁彎曲法以及超聲波測量法。其中靜態拉伸法又可分為光學測量和電學測量兩大類。動態共振法又可分為普通共振法、負載動態法、激光雙光柵法等幾類。梁彎曲法可分為激光光杠桿放大測量、單縫衍射法、霍爾傳感器測量法及光纖布拉格傳感器法等[3]。當前在高校教學和拓展研究中，光學測量被大量研究：光杠桿法[4]、莫爾條紋測量法[5]、等厚干涉法[6，7]、邁克耳孫干涉法[8，9]、雙縫干涉法[10]、數字激散斑法[11，12]、數字全息比較法[13]、光纖傳感器法[14]、光柵衍射法[15]等。其中干涉法具有很好的精度，但是光學拉伸法普遍存在實驗裝置穩定性低、鋼絲伸長存在延遲導致誤差、實驗操作過于復雜等缺點[3]。本文將設計基于拉伸法并利用劈尖干涉法測量微小形變量，測金屬絲楊氏模量的實驗裝置。我們首先在拉伸法的楊氏模量測定儀器的基礎上，設計制作合適的劈尖，同時結合JCD-3型讀數顯微鏡和CCD 視像系統作為穩定的測量讀數裝置，設計合理的測量方法，測量微小形變量造成的劈尖干涉圖樣的變化，精確測量出金屬絲的微小形變量，最后求出金屬絲的楊氏模量。本實驗設計巧妙，讀數穩定、操作簡便，推廣性實用性強。

2 實驗設計與實現

本實驗裝置包括JCD-3型讀數顯微鏡、鈉燈、楊氏模量測定儀、數字拉力計、螺旋測微器、卷尺、游標卡尺，及光學玻璃a、b。

1） 劈尖制作

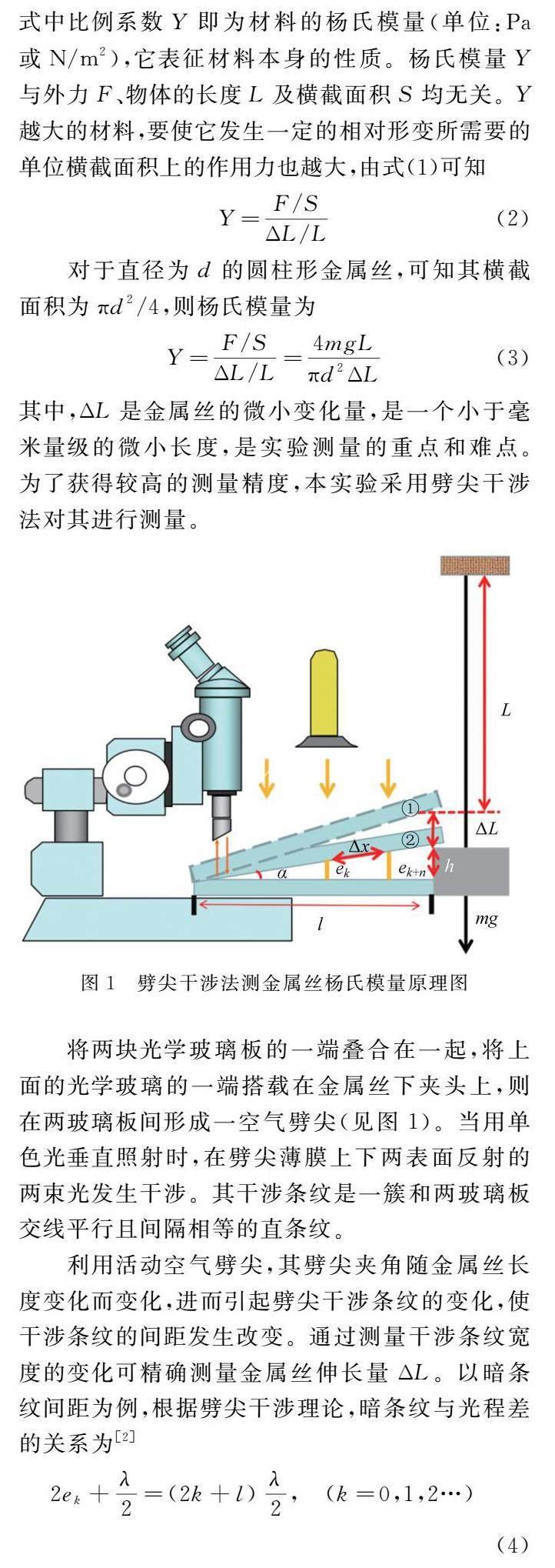
如圖2所示，將劈尖設置在楊氏模量測定儀的下夾頭的實驗平臺上;準備兩塊光學玻璃a、b，規格分別為150mm×20mm×4mm，130mm×20mm×4mm。將長度為150mm 的玻璃a固定在實驗平臺上，將長度為130mm 的玻璃b一端置于實驗平臺在金屬絲下夾頭處，另一端與玻璃a相接形成劈尖;在a、b光學玻璃接觸點后面，用橡膠圈套在a支撐b的末端，避免b產生向后相對滑動。劈尖的初始夾角的大小可通過拉力計施加拉力調節夾頭高度進行微調，達到形成清晰劈尖干涉的合適角度。

2） 裝置搭建

如圖3所示，將楊氏模量測定儀置于水平桌面，連接數字拉力計為金屬絲提供拉力;在金屬絲下夾頭的實驗平臺放置劈尖，JCD-3型讀數顯微鏡連接CCD視像系統，放置讀數顯微鏡使其物鏡在待觀測劈尖的正上方;將鈉燈置于裝置一側，使光源最亮的部分照在劈尖位置。

3） 實驗測量

（1） 調整讀數顯微鏡。首先，打開數字拉力計和鈉燈開關，預熱10分鐘。調節鈉燈光源的高度和方向;調整讀數顯微鏡物鏡下方的半反半透鏡，使讀數顯微鏡內視場最亮。調節目鏡聚焦，使十字交叉絲清晰。

（2） 調整劈尖厚度。緩緩調節旋轉數字拉力計的施力螺母，給金屬絲施加預拉力，使金屬絲拉直并且調整劈尖夾角，使干涉條紋清晰、條紋間距適中，以便于測量暗條紋條數;同時調整讀數顯微鏡的焦距，觀察CCD視像中的干涉圖樣，直至一個清晰穩定的干涉圖樣為止;最后將數字拉力計調零。

（3） 測量微小伸長量。緩慢旋轉施力螺母，逐漸均勻增加金屬絲拉力，每次增加0.20kg，須等待讀數穩定后，轉動讀數顯微鏡的讀數手輪，測出相鄰20條干涉暗條紋間距Δxi，取不同位置測兩組暗條紋間距;重復以上步驟，共施加拉力8次，直到增加至數字拉力計讀數為1.40kg;注意在每次增加拉力都需調整讀數顯微鏡焦距使干涉條紋清晰。

（4） 測量其他物理量。取金屬絲不同位置不同方向，利用螺旋測微器測量其直徑d。利用卷尺測量金屬絲在施加預拉力后的原長L。利用游標卡尺測量劈尖夾角到金屬絲下夾頭的距離l。

（5） 測量完畢。放松施力螺母，使金屬絲自由伸長，并關閉數字拉力計與鈉燈。

4 結語

本文通過測量干涉條紋間距的變化測量微小形變量的大小，從而測得金屬絲楊氏模量。該方法原理清晰，設計精巧;讀數望遠鏡的精度達到10-5m，實驗結果準確性較高;借助CCD 視像系統讀數不僅使讀數便捷，同時也減小人為因素對干涉平臺的影響，顯著增加儀器操作的穩定性。實驗的測量采用逐步均勻適中的施力，多組讀數，多次測量的方法，減小了金屬絲材料發生塑性形變得可能和形變的遲滯特性帶來的影響，同時減小單次施力可能造成的人為因素的不穩定性。最后，從計算結果對比學校本科學員采用光杠桿放大法測得實驗數據的統計（相對不確定度在5%～10%之間，平均相對不確定度約6.2%，最佳結果的相對不確定度約5%），可以認為本次利用劈尖干涉對楊氏模量測定儀的改進，為微小量的測量提供了新的思路，確實提高了楊氏模量測量的精度。同時，本次實驗設計也是對課堂教學的很好鞏固和拓展，完成了從理論知識到實驗學習，再到實踐拓展的學習閉環，在課堂實驗教學中具有很好的教學推廣價值。

目前世界上比較先進的幾款坦克，比如豹2A6、M1A2SEP等，炮塔正面防穿甲能力大概在600～700 毫米范圍。我國99A 坦克防護力在1000毫米范圍。這得益于其新型復合裝甲。復合裝甲是由幾種物理性能不同的材料，按照一定的層次比例復合而成，依靠各層材料之間物理性能的差異來干擾來襲彈丸（射流）的穿透，消耗其能量，最終達到阻止彈丸（射流）穿透的目的。復合裝甲的性能受很多參數影響，其中彈性模量對材料性能的影響尤為突出。為了檢驗本實驗設計方案的實用性和有效性，我們計劃在后續的研究中，測量我國99A 坦克的復合裝甲的彈性模量。

參 考 文 獻

[1] 劉建林，夏熱.托馬斯· 楊之力學貢獻[J].力學與實踐，2011，33（3）：84-86.

LIU J L， XIA R. Thomas Yangs contribution to mechanics[J].Mechanics and Practice， 2011，33（3）：84. （in Chinese）

[2] 白忠，李延標，林上金.大學物理實驗[M].7版.北京：高等教育出版社，2018.

[3] 段陽，楊浩林，伍泓錦，等.楊氏彈性模量測量實驗綜述[J].物理與工程，2020（3）：89-102.

DUAN Y， YANG H L， WU H J， et al. Summary ofYoungs elastic modulus measurement experiment[J]. Physicsand Engineering， 2020， 30（3）： 89-102. （in Chinese）

[4] 黃菊，梁小沖.拉伸法測鋼絲楊氏模量實驗儀器的改進[J].實驗科學與技術，2018，16（5）：178-184.

HUANG J， LIANG X C. Improvement of tensile methodfor measuring Youngs modulus of steel wire[J]. ExperimentalScience and Technology， 2018， 16（5）： 178-184. （inChinese）

[5] 隗群梅，孟德迎，何立志.雙光柵在不同夾角下測量楊氏模量的實驗研究[J].大學物理實驗，2017，36（8）：41-45.

WEI Q M， MENG D Y， HE L Z. Experimental study onmeasuring Youngs modulus with double gratings at differentangles[J]. University Physics Experiment， 2017， 36（8）：41-45. （in Chinese）

[6] 賴學輝，梁詠棋，蘇文青，等.利用等厚干涉測量鋼絲的楊氏模量[J].大學物理實驗，2019，32（1）：50-52.

LAI X H， LIANG Y Q， SU W Q， et al. Measurement ofYoungs modulus of steel wire using equal thickness interference[J]. College Physics Experiment， 2019， 32（1）： 50-52. （in Chinese）

[7] 許巧平.劈尖干涉法測量金屬絲楊氏模量[J].大學物理，2016，35（4）：30-32.

XU Q P. Measurement of Youngs modulus of metal wire bywedge interference[J]. University Physics， 2016， 35（4）：30-32. （in Chinese）

[8] 李儒頌，葉文江.金屬絲楊氏模量測量裝置的設計[J].大學物理實驗，2014，27（5）：51-53.

LI R S， YE W J. Design of measuring device for Youngsmodulus of metal wire[J]. College Physics Experiment，2014， 27（5）： 51-53. （in Chinese）

[9] 徐勛義，張祖豪，劉子健，等.基于邁克耳孫涉的金屬絲楊氏模量測量[J].物理實驗，2016，36（9）：19-22.

XU X Y， ZHANG Z H， LIU Z J， et al. Measurement ofYoungs modulus of metal wire based on Michael Suns theory[J]. Physical Experiment， 2016， 36（9）： 19-22. （in Chinese）

[10] 方運良，崔娟，朱偉玲.雙縫干涉法測量金屬的楊氏模量[J].物理實驗，2014，34（1）：37-39.

FANG Y L， CUI J， ZHU W L. Measurement of Youngsmodulus of metals by double-slit interferometry[J]. PhysicalExperiment， 2014， 34（1）： 37-39. （in Chinese）

[11] 汪濤，蔡小龍，李遠，等.數字激光散斑法測量楊氏彈性模量的實驗設計[J].激光與紅外，2017，47（10）：1201-1204.

WANG T， CAI X L， LI Y， et al. Experimental design ofmeasuring Youngs modulus of elasticity by digital laserspeckle method[J]. Laser and Infrared， 2017， 47（10）：1201-1204. （in Chinese）

[12] 韓艷嬌，劉憲.利用數字散斑照相術測量金屬絲楊氏模量[J].河南科學，2016，34（11）： 1884-1888.

HAN Y J， LIU X. Measuring the Youngs modulus ofmetal wire by digital speckle photography[J]. Henan Science，2016， 34（11）： 1884-1888. （in Chinese）

[13] 嚴琪琪，陳彥，胡湘，等.數字全息比較法測量鋁板的楊氏模量[J].大學物理，2018，37（10）：25-29.

YAN Q Q， CHEN Y， HU X， et al. Measurement ofYoungs modulus of aluminum plate by digital holographiccomparison method[J]. College Physics， 2018， 37（10）：25-29. （in Chinese）

[14] 葉天明，周穎東，潘寧，等.用光纖傳感器測量金屬絲的楊氏模量[J].物理實驗，2015，35（12）：36-38.

YE T M， ZHOU Y D， PAN N， et al. Measurement ofYoungs modulus of metal wire using optical fiber sensor[J]. Physical Experiment， 2015， 35（12）： 36-38. （in Chinese）

[15] 孟赟，鄧文浩，秦鵬程，等.基于光柵衍射的彈性模量小角度測量[J].物理實驗，2017，37（6）：54-57.

MENG Y， DENG W H， QIN P C， et al. Small anglemeasurement of elastic modulus based on grating diffraction[J]. Physical Experiment， 2017， 37（6）： 54-57. （inChinese