基于諧響應分析的調節器殼體動態特性研究與改進

馮 濤,楊軍杰,趙 彬,賈 佳

(中國航發西安動力控制科技有限公司,西安 710077)

0 引言

正弦振動是隨時間按正弦(或余弦)函數變化的振動,常出現在存在旋轉、脈動、振蕩現象的電子產品和艦船、飛行器、各類車輛等裝置上[1]。航空燃油調節器做為飛機發動機附件設備因受到飛機發動機高速旋轉振動載荷變化產生周期振動激勵,對其結構會產生直接影響,嚴重的會造成機體振動斷裂破壞。采用諧響應分析方法可以用來研判共振的發生,提前采取措施,減小共振以及其他受迫振動引起的有害現象,從而保證設備的安全穩定[2],因此正弦振動試驗是考察航空產品結構可靠性設計和環境適應性要求的主要內容之一。

現有某型航空燃油泵調節器,其作為航空發動機燃油附件安裝在發動機附近承受發動機振動帶來的正弦載荷,其殼體在正弦振動試驗階段出現殼體開裂,為了適應機載環境的性能與結構可靠性要求,需要對問題產品改進設計。本文通過仿真手段,建立試驗件的振動試驗仿真模型,分析產品在正弦振動載荷條件下的振動響應,并通過實際試驗與仿真結果進行對比,驗證仿真分析的可行性,對比改進結構與原結構的動態特性,分析產品振動性能薄弱環節,檢驗產品振動安全裕量,并進行了多次減振優化仿真分析,為產品結構動力學設計提供參考,所做工作幫助提高了產品抗振性能。

1 正弦振動的數學描述

航空燃油泵調節器受發動機旋轉振動載荷產生周期振動激勵。

振動系統可看成由質量、彈簧和阻尼器組成,一般認為彈簧與阻尼器皆為線性元件,即彈性力與位移成正比,阻尼力與速度成正比,具有比例阻尼的多自由度系統其運動方程為[3]:

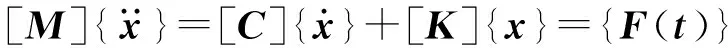
(1)

其中:[C]=α[M]+β[K],α和β為比例常數; [C]為阻尼矩陣,復合式的阻尼稱為比例阻尼;[M]和[K]分別為質量矩陣和剛度矩陣;F(t)表示激振力。

一般情況下旋轉機械受到的動載皆為周期性激擾,可視為簡諧力,當激振力為簡諧力時,即F(t)=f(t)sin(ωt),加入簡諧載荷下受迫振動的運動微分方程為:

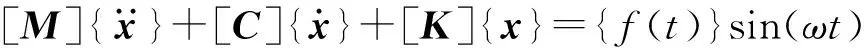
(2)

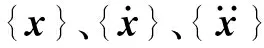
移響應方程為:

{x}={A}sin(ωt+φ0)

(3)

其中:φ0為位移響應滯后激振力的相位角;{A}為位移幅值向量。

將式(3)代入式(2)得:

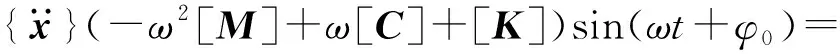
諧響應分析用于確定結構在承受隨時間按正弦變化的載荷時的穩態響應,在一定頻率ω范圍及間隔下,通過有限元軟件對上述方程的求解,能夠計算出相應振動位移,從而得出振幅-頻率關系,進而根據曲線得出峰/谷值頻率。通過振動諧響應分析,還可得出應力、應變及加速度與激振頻率之間的響應曲線,能夠幫助預測結構的持續動力特性,從而驗證其設計是否能夠克服疲勞、共振及其他受迫振動引起的有害結果[4]。

2 調節器諧響應分析

本文以某型航空燃油泵調節器殼體為例,在前期振動試驗基礎上,通過對整機有限元仿真模型的標定調試,根據仿真結果,對其殼體結構在工作狀態下的振動進行了分析、標定與優化。

在我國跨境電商物流的發展過程中，基礎設施的不完善及體系不完整等，物流的成本較高，根據相關資料得出結論，從成本來看，我國跨境電商物流的成本遠遠高于其他國家甚至是國際標準。跨境電商物流需要考慮的問題多而復雜，涉及國內物流、國內海關、 國際運輸、 國外海關、 國外物流眾多環節，在實際操作中風險很大，因此，在一定程度上大大增加了我國跨境電商的物流成本。

2.1 振動分析模型建立

根據該調節器幾何結構,建立調節器組件裝配模型如圖1所示。調節器殼體組件在進行振動實驗時,依靠12個螺釘將殼體組件固定在振動實驗臺工裝上。

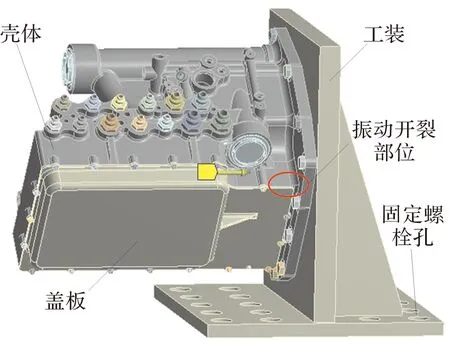
圖1 調節器組件裝配模型

根據振動試驗中組件的實際安裝情況,設置工裝底板螺栓孔區域為固定約束。分析時,振動載荷通過工裝底板約束施加,振動載荷X、Y、Z三個方向分別按最大20g施加。

2.2 阻尼比的選取

在進行諧響應分析中,振動系統的阻尼比的確定是關鍵問題,工程中阻尼比經常是取經驗值,容易造成分析結果跟實際不符。阻尼對模態頻率的影響很小,其主要作用是降低共振處的振幅,阻尼越小,共振的振幅會越大,阻尼比的確定也影響著對系統分析結果的評定。

目前阻尼問題研究的還不是很透徹,并沒有很多的理論支持,本文結合試驗測試的數據,采用半功率法估算出調節器組件結構的阻尼比,并以此進行諧響應分析。

半功率帶寬法是根據簡諧振動系統共振時的振幅放大因子曲線來推算阻尼比,特別是在環境激勵的情況下,被廣泛用于測量結構阻尼比。其計算公式如下[5]:

a、b兩點稱為半功率點,這兩點所對應的頻率為:

或(fa/fn)2=1-2ξ,(fb/fn)2=1+2ξ

由此可得:

由于在小阻尼情況下fa≈fn≈fb,所以,

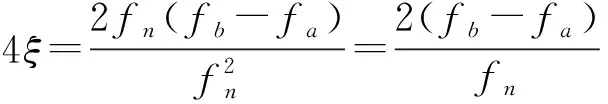
其中:ξ為阻尼比;fn為系統共振頻率;H是共振峰幅值,fa、fb是幅值為0.707H時所對應的兩個頻率點[6-7]。

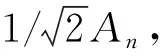
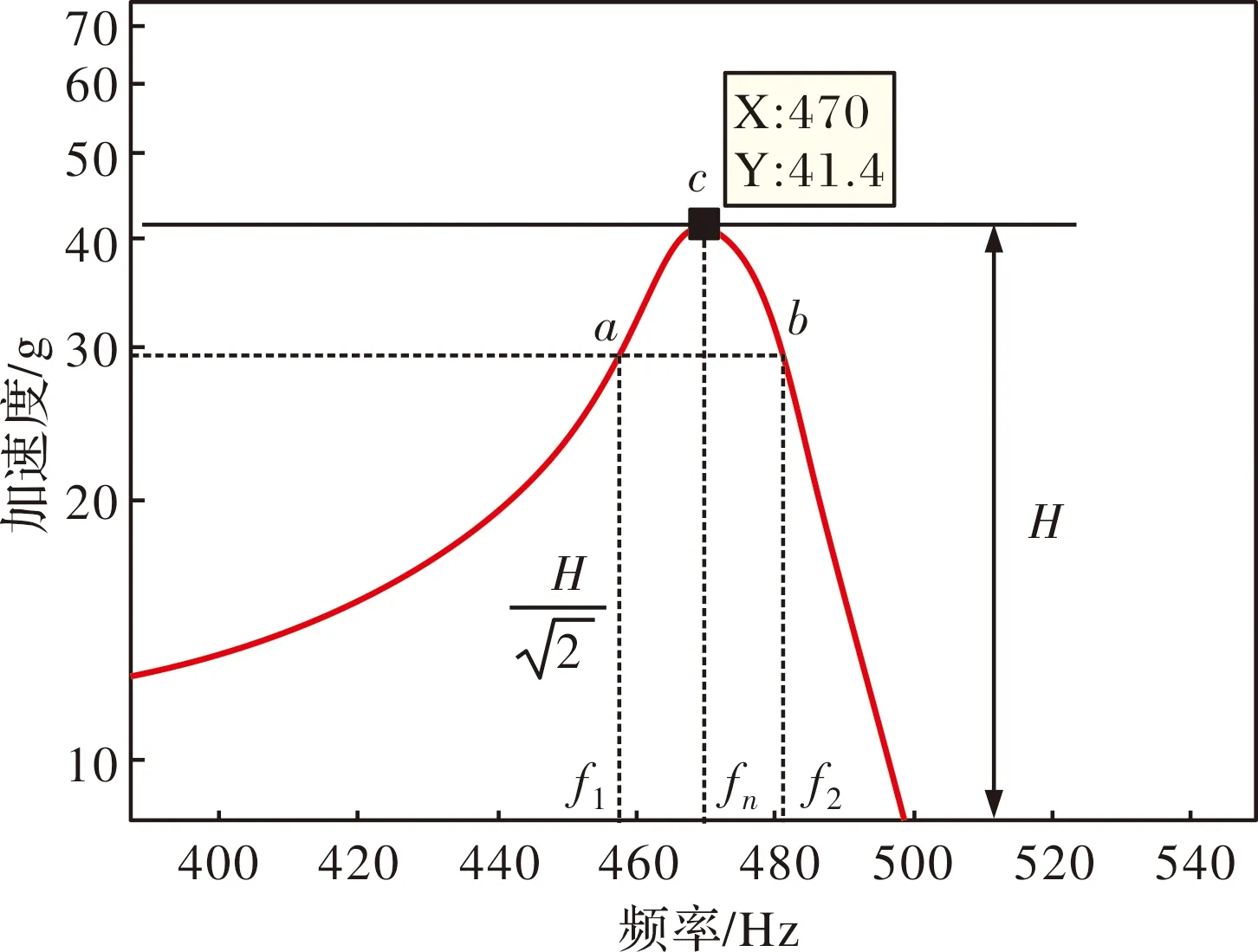
圖2 振系的幅頻特性及半功率點

通過上述公式和試驗實測峰值數據,計算出調節器組件裝配模型的阻尼比為:

將該阻尼比應用到調節器裝配組件三個方向的諧響應分析,得到原殼體傳感器位置處的仿真頻響曲線與試驗曲線。X方向振動和試驗頻響曲線對比如圖3所示,Y方向振動和試驗頻響曲線對比如圖4所示,Z方向振動和試驗頻響曲線對比如圖5所示。

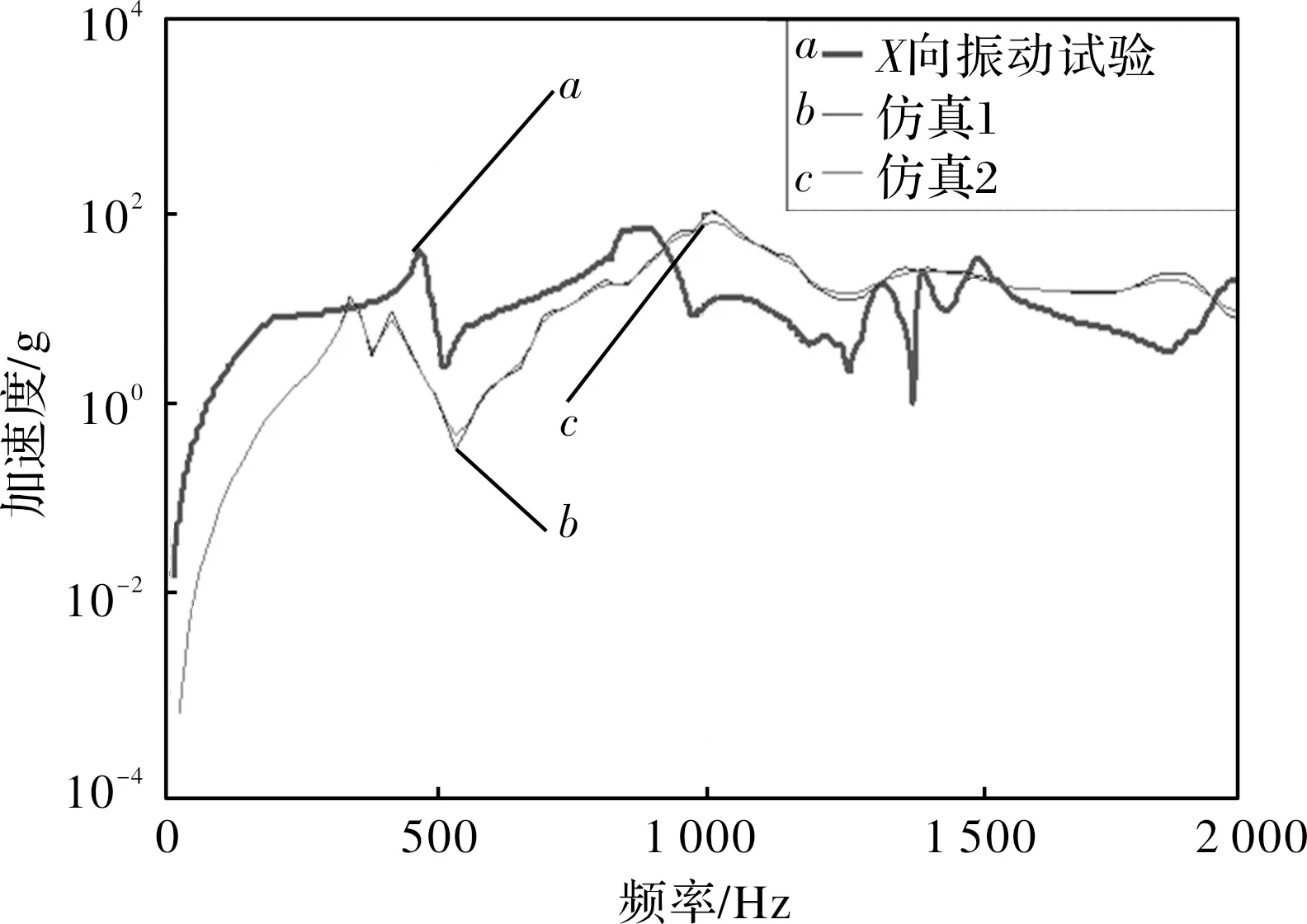
圖3 X方向振動和試驗頻響曲線對比

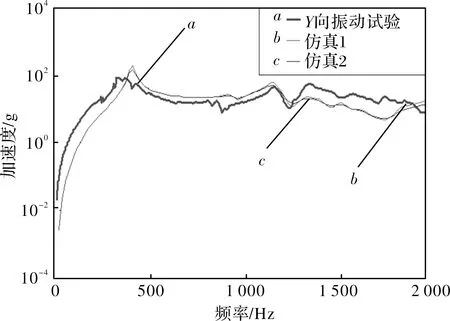
圖4 Y方向振動和試驗頻響曲線對比

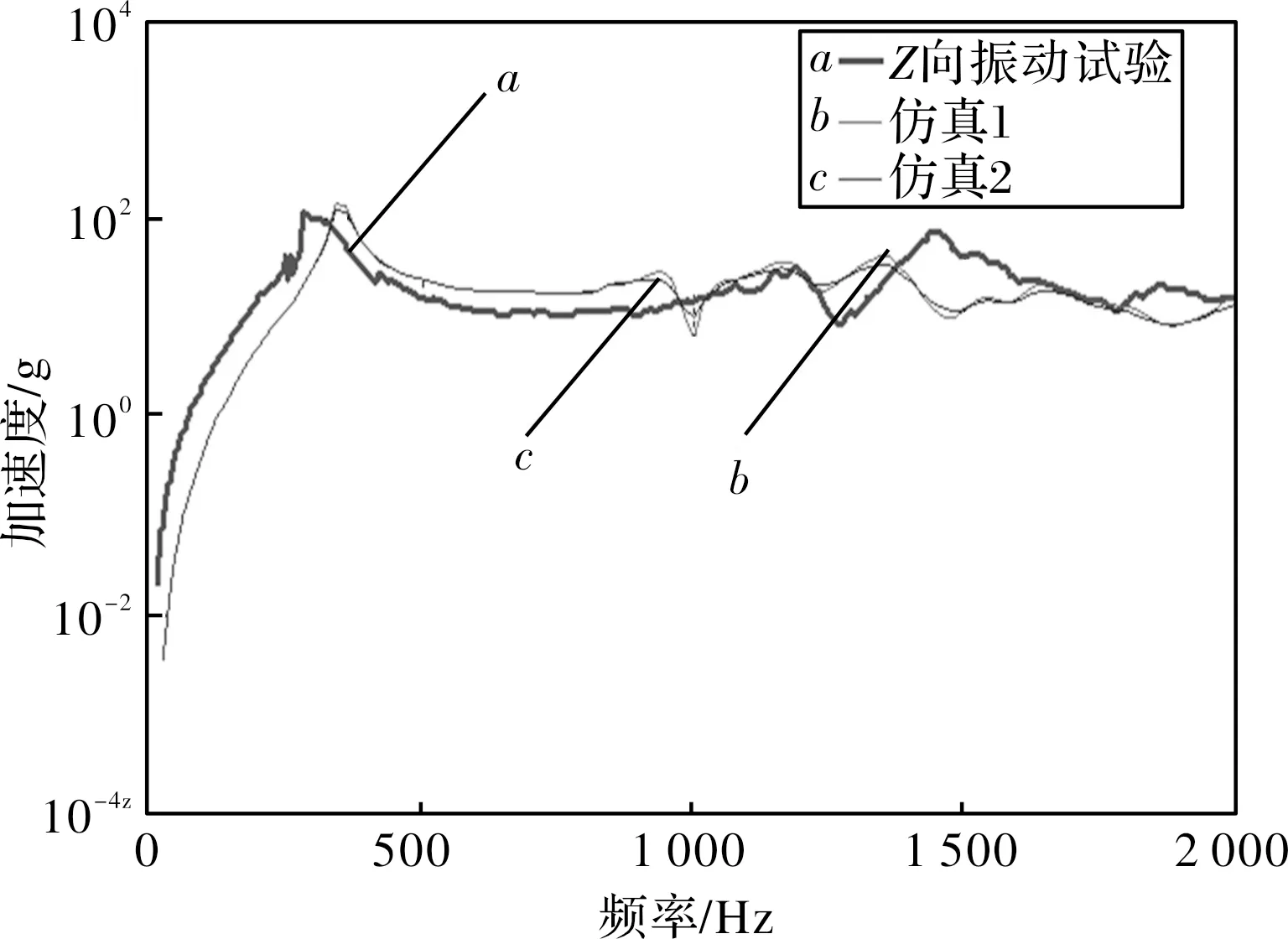
圖5 Z方向振動和試驗頻響曲線對比

從3個方向振動試驗和仿真加速度頻響曲線對比可見,3個方向仿真和試驗頻響曲線趨勢相對一致,其中X向偏差相對較大,Y、Z向吻合較好。仿真1和仿真2是阻尼比分別為0.01、0.02下的曲線,阻尼比對系統振動加速度幅值有一定影響,阻尼比越大振幅越小。得到殼體結構第一階頻率為186.85 Hz,最大響應73.2g。總結可知,仿真結果有一定的精度,測點的加速度與試驗結果有一定偏差,這與整體結構裝配邊界模擬、各部件連接特性以及阻尼設定有關,同時由于仿真計算基于線性假設,而實際試驗時結構接觸間難免會出現一定程度的非線性,這就難以保證仿真和試驗保持一致。

3 結構優化設計

該調節器殼體在正弦振動試驗時,其殼體在Z向振動試驗階段底部出現殼體開裂,振動開裂部位位于圖1圈中所示部位。由于該殼體結構較長,底部固定后形成較大懸臂結構,同時因內部油路和減重需要,在底部中間部位存在較大挖空設計,這影響了殼體底部抵抗變形的剛度,造成殼體在外部載荷作用下激發出較大的振動,靠近底部的尖角部分承受了較大振動應力,容易發生破壞。

為了改善調節器殼體在工作過程中的振動性能,需要提升其最大加速度部位后端的剛度,減小殼體振動加速度。因此在控制整體重量的前提下,結合標定完成的有限元模型,對加速度較大的部位進行針對性的多方案優化分析。

優化方向主要從兩方面考慮:一是提高殼體薄弱部位的剛度,采取的措施如設置加強筋、增加壁厚、減少破壞結構連續的孔洞;二是盡量降低整體結構重心,調整功能布局,減少懸臂效應。

對優化前后兩種殼體結構做了諧響應分析對比,優化前后6階固有頻率對比如表1所示。對出現故障的Z向諧響應振動,調節器殼體改進前后Z向正弦振動仿真應力云圖如圖6所示。從表1中對比可以看出,優化后殼體前6階頻率都有很大的提高,1階提高了26.9%。出現殼體開裂的Z向受載時進行正弦振動仿真分析,優化前殼體等效應力云圖顯示最大應力為182.02 MPa,其余部位應力值相對較小,從圖中可以直觀看出試驗件上的應力的最大位置位于殼體底部轉角處,這與實際開裂部位一致;其主要原因為電氣部位的薄壁腔承擔了類似加強筋的作用,處于殼體的主要承力部位,由于該薄壁腔自身強度不足,導致在振動試驗中產生裂紋。優化設計中,將殼體的電氣腔遠離承力部位,避免電氣腔的薄壁結構出現應力集中的情況,以提高產品的強度能力。優化后的振動等效應力云圖也顯示殼體整體振動應力得到降低。

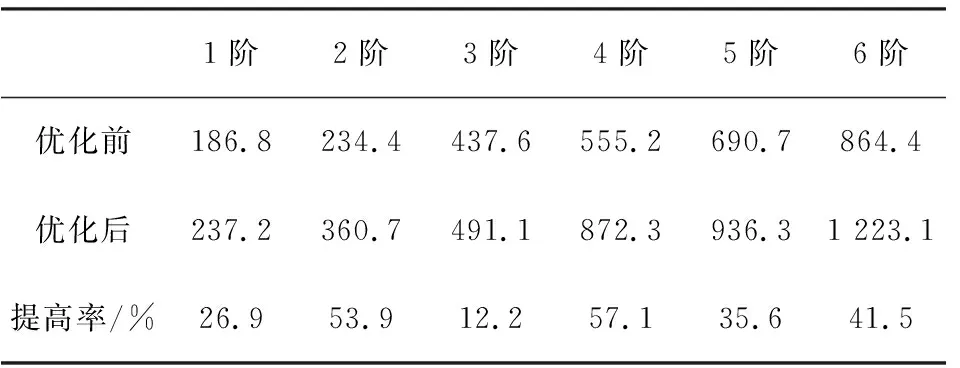
表1 優化前后6階固有頻率對比(Hz)

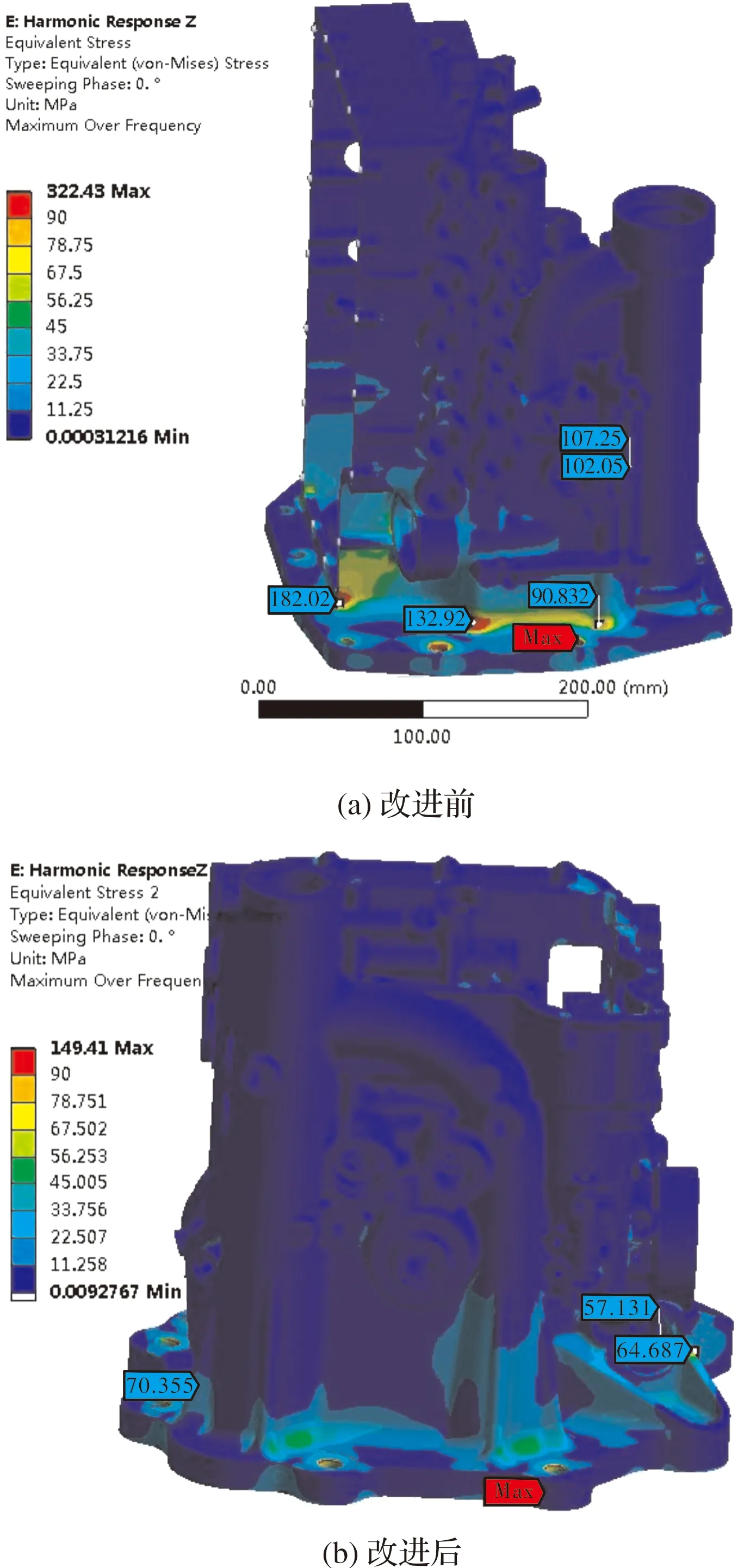
圖6 調節器殼體改進前后Z向正弦振動仿真應力云圖

4 結論

通過對調節器組件諧響應振動試驗的仿真分析,并與真實試驗結果進行對比修正,印證了殼體開裂的試驗現象,找出了殼體振動失效機理和改進方向;借助仿真對改進件的響應峰值頻率及振動應力大小進行預測,使設計結果可視化,有助于設計人員對產品進行優化,改進后的新殼體底部設置加強筋的結構形式及調整功能布局、降低整體高度,重量減輕,經仿真分析及試驗驗證,結構強度富裕,抗振能力得到提高。