基于響應曲面法的DPF捕集性能多目標優化

黃粉蓮,李玲玲,夏大雙,佘超杰,萬明定,畢玉華

(昆明理工大學云南省內燃機重點實驗室,云南 昆明 650500)

柴油機因其輸出扭矩大、熱效率高、經濟性好、工作可靠等特點,廣泛應用于交通運輸、國防裝備、工農業機械等領域[1-2]。然而,柴油機運行過程中會產生大量的顆粒物(Particulate Matters,PM)排放,對人類健康和環境構成重大威脅[3]。柴油機顆粒捕集器(Diesel Particulate Filter,DPF)是目前公認的能夠有效降低柴油機顆粒物排放的關鍵后處理裝置[4-5]。隨著顆粒物在DPF內部不斷沉積,DPF前后壓降致使發動機排氣背壓升高,流動阻力增大,甚至導致燃燒過程惡化,發動機經濟性、動力性和排放性能下降[6-7]。DPF結構參數是影響DPF捕集性能和流動阻力的主要因素[5]。優化DPF的結構設計,提高DPF捕集效率,同時有效降低壓降,對減少柴油機PM排放和提升經濟性能具有重要意義。

國內外研究學者針對DPF結構優化設計進行了廣泛且深入的研究。Basu等[8]建立了一維DPF通道模型,研究了不同壁面滲透率、通道數量和孔隙率對DPF捕集性能的影響,結果表明:隨著孔隙率和壁面滲透率的增加,DPF捕集效率增加;隨著通道數量的減少,DPF進出口氣體流速降低,壁內氣體滲透速度降低。白曼等[9]研究了不同比例孔結構下DPF壓降特性,結果表明:使用非對稱孔結構可以有效提高炭煙和灰分容量,降低DPF壓降。Xiao等[10]提出了一種非對稱孔道顆粒捕集器,其孔道橫截面形狀由六邊形、矩形及三角形組成,研究表明,新型非對稱孔道顆粒捕集器可以通過提高過濾壁的利用率和過濾壁面表面積來有效降低壓降。湯東等[11]借助DPF再生模型研究了DPF 結構參數和運行參數對再生性能的影響,評估了結構參數與運行參數對再生性能影響的顯著性。Zhang等[12]為了提高DPF的整體性能,基于壓降、再生性能等目標函數,利用自適應變尺度混沌優化算法對DPF進行優化設計,結果表明:優化后DPF的壓降減少了14.5%,再生效率提高了17.3%。

目前針對DPF捕集性能的結構參數優化研究主要涉及單個結構參數對多個性能的影響或多個參數對單個性能的影響,缺乏多參數交互影響和多目標優化研究,且大多數研究方法都采用控制變量法,無法同時優化多個目標。本研究以最大壓降和初始過濾效率為優化目標,以結構參數孔隙率、孔直徑、壁厚、過濾體長度以及過濾體直徑為優化變量,提出基于響應面模型的DPF捕集性能多目標優化方法,建立了基于最大壓降和初始過濾效率目標函數的DPF捕集性能多目標優化模型,根據響應曲面回歸方程分析了DPF結構參數對最大壓降和初始捕集效率的交互作用,采用滿意度函數法進行多目標參數優化。研究結果可為優化DPF結構設計、提高捕集性能提供理論支持。

1 數值模型理論

DPF顆粒物加載模型的物理結構見圖1,顆粒過濾器 DPF 由進氣管、多孔介質過濾器和排氣管3個主要部分組成,其核心部件是多孔介質過濾器,它是決定 DPF 捕集效率以及壓降的關鍵。多孔介質過濾器采用壁流式結構,由一系列交替堵塞的入口和出口通道組成。圖2示出壁流式過濾載體通道示意。當柴油機廢氣從入口通道經過過濾壁流入出口通道時,廢氣中的顆粒物會被多孔過濾壁截留,并沉積在入口通道的過濾壁上,從而達到凈化廢氣的目的。

1—進氣管;2—多孔介質過濾器;3—排氣管。圖1 DPF結構示意

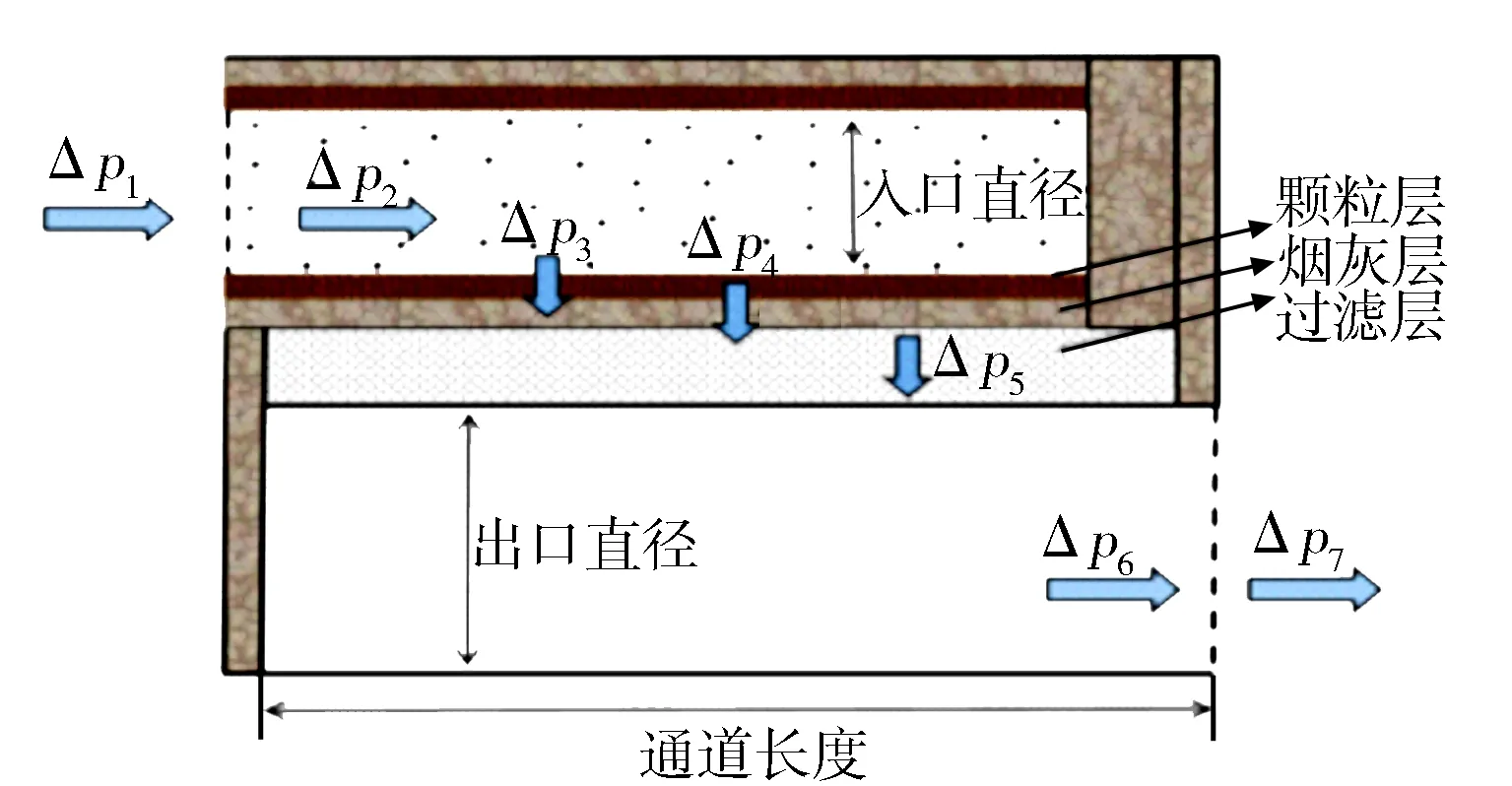
圖2 DPF進出口通道示意

1.1 壓降數學模型

針對壁流式柴油機顆粒過濾器,GT-Power軟件中提供了合適的壓降計算模型與炭煙捕集模型,能夠準確預測DPF加載過程中的總壓降和炭煙捕集量。發動機排氣流經DPF的總壓降Δp滿足達西定律[13],主要由7個部分組成,其計算公式見式(1)。

Δp=Δp1+Δp2+Δp3+
Δp4+Δp5+Δp6+Δp7。

(1)

式中:Δp1,Δp7分別為氣體流入通道時的收縮損失和流出通道時的膨脹損失;Δp2,Δp6分別為入口和出口通道中摩擦引起的壓力損失;Δp3為氣體通過顆粒層的壓力損失;Δp4為氣體通過煙灰層的壓力損失;Δp5為氣體通過過濾層的壓力損失。

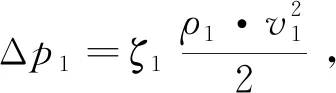
(2)

(3)

(4)

(5)

(6)

(7)

(8)

式中:ζ1,ζ2分別為氣體流入通道和流出通道摩擦損失系數;vw,1為入口通道壁面流速;μ為排氣的黏性系數;d1,d2分別為進出口通道直徑;kw為過濾層滲透率;kac為煙灰層滲透率;ksc為顆粒層滲透率;δw為壁面厚度;δac為煙灰層厚度;ρ1,ρ2為入口和出口通道氣流密度;v1,v2為入口和出口孔道氣體流速;ρg,1,ρg,2分別為孔道入口與出口氣流密度;L為孔道有效長度。

1.2 炭煙捕集數學模型

DPF炭煙捕集模型主要基于布朗擴散和直接攔截捕集機理,DPF的綜合捕集效率按下式計算:

k=1-e-α,

(9)

(10)

式中:δ是過濾壁的厚度;d是過濾壁的微孔直徑;ε是過濾壁的孔隙率;η是過濾壁的綜合捕集系數。

2 仿真模型的建立與驗證

2.1 試驗設備

DPF微粒加載試驗采用一臺D20TCI柴油機,其主要技術參數見表1,DPF主要參數見表2。采用瞬態循環測試工況來進行炭煙加載試驗,達到滿載狀態加載時間約為11 h。試驗中利用壓力傳感器監測DPF前后兩端壓降損失,利用電子天平對不同加載時間段的DPF進行熱稱重。試驗測試設備見表3。

表1 發動機主要技術參數

表2 DPF主要基本參數

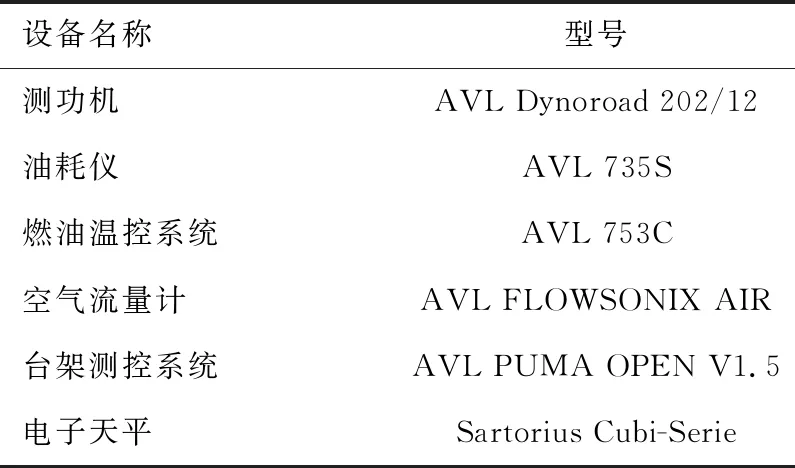
表3 試驗用測試設備

2.2 模型建立

利用GT-Power建立DPF一維捕集模型(見圖3),該模型分為進口邊界模塊、出口邊界模塊、DPF 顆粒物加載模塊、壓降損失及捕集效率監控模塊。根據試驗采集的發動機排放數據標定模型仿真邊界,DPF入口和出口邊界設置相應的大氣壓力、大氣溫度與氣體組分。

圖3 DPF一維仿真模型

2.3 仿真模型驗證

為驗證仿真模型的準確性,試驗中選取6個時間點來測量DPF炭煙加載量。由于DPF炭煙加載試驗耗時過長,為了縮短仿真時間,故將模型中顆粒噴射器噴射的炭煙濃度設置為0.124 kg/h,排氣流量為150 kg/h,排氣溫度為600 K,仿真時間為600 s。通過對比DPF捕集過程中壓降損失的仿真結果與試驗數據,對DPF捕集模型進行驗證,結果見圖4。由圖4可知,仿真值與試驗值的誤差均小于5%,且壓降變化趨勢符合Shigeki Daido提出的三層壓降損失理論[14],因此所建立的DPF捕集模型準確、有效,可用于進一步的DPF捕集性能分析與參數優化。

圖4 DPF捕集階段壓降損失模擬值與試驗值的對比

3 基于響應面法的參數優化

響應面法(Response Surface Methodology,RSM)是一種結合統計與數學理論來分析多因素多響應問題的試驗設計方法,該方法通過合理的試驗設計得到相應試驗數據,并擬合自變量和因變量之間的函數關系建立響應面回歸模型,從而對影響過程的因子及其交互作用進行評估與優化[15]。DPF捕集性能的優化方法見圖4。優化過程主要分為3個部分:1)通過GT-Power構建DPF捕集性能仿真模型,根據發動機臺架試驗對仿真模型進行驗證;2)基于Box-Behnken試驗設計構建響應面回歸模型,對擬合的回歸模型進行診斷分析,并對結構參數的顯著性與交互作用進行研究;3)利用滿意度函數法對響應函數進行轉化,得到目標函數,對目標函數進行最大化尋優,獲得優化設計參數。

圖5 響應面法優化流程

3.1 確定優化目標和優化變量

DPF低壓降和高捕集效率的優化設計是保證發動機具有良好經濟性能與排放性能的關鍵,而最大壓降與初始捕集效率能夠很好表征DPF捕集效率和壓降的整體情況[16],因此,將最大壓降最小化與初始捕集效率最大化作為DPF捕集性能的優化目標。參照已有的DPF捕集性能單因素影響研究結果[17-19],選取對捕集效率和壓降有重要影響的5個關鍵結構參數作為優化變量,以加載試驗所用的DPF結構參數為初始值,參考GT-Power軟件中提供的設計經驗值選取變量的優化范圍,具體優化變量的初始值和優化范圍見表4。

表4 變量的初始值和優化范圍

3.2 響應面試驗設計

響應面法優化采用Box-Behnken設計(BBD)方法,BBD試驗設計方法具有試驗次數更少,效率更高,有效降低試驗成本的優勢[20]。以DPF最大壓降和初始捕集效率為評價指標,孔隙率、微孔直徑等5個結構參數為研究對象,進行五因素三水平試驗,試驗設計因子及水平編碼見表5。根據BBD試驗設計需求,共進行46次試驗,試驗結果利用DPF捕集模型計算獲取,由于試驗組數較多,僅給出部分試驗設計方案及結果(見表6)。

表5 試驗設計因子及其水平編碼

表6 部分試驗設計方案及結果

3.3 擬合響應面模型

根據試驗設計和仿真結果,擬合自變量和因變量之間的函數關系建立響應曲面二階回歸方程[21]。采用二階多項式擬合得到的壓降實際因子回歸方程見式(11),捕集效率實際因子回歸方程見式(12)。

y1=+80.454 85+8.052 28A+0.361 98B-
0.270 49C+73.488 41D-0.803 62E+
0.156 44AB-0.088 985AC+0.684 52AD-
0.204 77AE-5.717 61×10-4BC+
0.089 318BD-5.717 61×10-4BE-
0.111 18CD-1.228 77×10-3CE-
0.529 11DE+32.727 67A2+34.022 33D2-
4.533 90×10-3B2+3.710 80×10-4C2+
2.416 41×10-3E2。

(11)

y2=-0.613 16+2.020 64A-0.110 70B+
4.276 14×10-3C-2.460 11×10-3AC+
0.010 024E+0.066 305AB-1.844 62AD+
3.385 01D+0.086 287BD+2.729 43BE-
5.968 79×10-3AE+1.119 99×10-4BC-
3.032 03×10-3CD-9.882 92×10-6CE-
7.478 28×10-3DE-9.413 94×10-4B2-
4.642 91×10-6C2-2.434 28D2-
0.711 10A2-1.829 69×10-5E2。

(12)

3.4 響應面診斷及分析

響應面模型各優化目標的實際值和預測值見圖6和圖7。圖中的點表示模型的實際值,實線表示模型的預測值。模型實際值越接近45°斜線,模型的預測精度越高。通過分析可知,擬合的響應面模型具有較高精度,能夠準確反映DPF捕集性能響應規律。

圖7 捕集效率的實際值和預測響應值

表7 方差分析結果

3.5 結構參數顯著性分析

在DPF結構參數中,不同參數之間相互影響和制約,共同影響DPF最大壓降和初始捕集效率,為了在前期設計階段了解DPF捕集性能與結構參數之間的復雜關系,減小后期優化難度,需對影響因素進行顯著性分析。方差分析結果中的P值可以用于判斷結構參數對響應的影響是否顯著,編碼因子回歸方程系數可以直觀反映顯著性相對強弱。編碼因子回歸方程根據試驗設計和仿真結果擬合得到,最大壓降編碼因子回歸方程系數見圖8,圖中數值的大小代表參數對響應影響的程度,數值的正負代表對響應起到正面或負面作用。由圖8可知,各單參數對最大壓降的影響強弱順序為E>D>C>A>B,結合方差分析結果可知,孔直徑B對最大壓降的影響非常小(P≥0.05),其余4個參數對最大壓降影響顯著(P<0.05);兩參數對最大壓降的交互影響強弱順序為CE>DE>AD>AC>AE>CD>BC>BE>AB>BD,其中過濾體直徑E和其他參數之間的交互作用對最大壓降的影響最大,孔隙率A、過濾體長度C、壁厚D3個參數之間的交互作用對最大壓降也有顯著影響(P<0.05),孔直徑B與其他參數之間的交互作用不顯著(P≥0.05)。

圖8 最大壓降編碼因子系數

初始捕集效率編碼因子回歸方程系數見圖9。由圖9可知,單參數對初始捕集效率的影響強弱順序為B>D>A>E>C,5個結構參數對初始捕集效率都有顯著影響(P<0.05);兩參數對初始捕集效率的交互影響由大到小為AB>BD>BC>AD>BE>AC>AE>CD>DE>CE,5個結構參數之間的交互作用對初始捕集效率的影響都很顯著(P<0.05),其中孔直徑B和其他參數之間的交互作用最顯著。

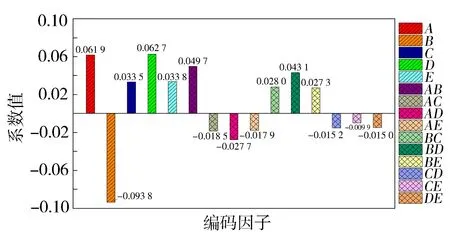
圖9 初始捕集效率編碼因子系數

3.6 結構參數的交互作用分析

由于影響最大壓降與初始捕集效率的結構參數之間存在交互作用,為進一步分析不同因素對響應的影響,通過三維響應面圖分析交互作用顯著的結構參數。圖10a示出孔隙率與壁厚在其余結構參數為零水平時對最大壓降的影響響應曲面。圖10a中響應曲面最大壓降的低值區向小孔隙率小壁厚方向傾斜,表明隨著孔隙率和壁厚的減小,DPF最大壓降減小。試驗中,孔隙率為0.38,壁厚為0.15 mm時DPF最大壓降最小,僅為3.17 kPa。圖10b示出孔隙率與過濾體直徑在其余結構參數為零水平時對最大壓降的影響響應曲面。由圖10b可知,隨著DPF孔隙率和過濾體直徑的減小,DPF最大壓降減小,且兩參數交互作用中過濾體直徑占主導因素,壁厚對最大壓降的影響隨過濾體直徑的增大逐漸減弱,過濾體直徑在0～1水平時,即使選擇較大孔隙率,DPF最大壓降仍能維持在10 kPa以下。因此,選用較大的過濾體直徑可有效降低最大壓降。圖10c示出壁厚與過濾體直徑在其余結構參數為零水平時對最大壓降的影響響應曲面。由圖10c可知,隨著孔隙率的減小和過濾體直徑的增大,DPF最大壓降減小,且最大壓降在高值區響應曲面坡度陡峭,在低值區響應曲面坡度平緩,表明較大的過濾體直徑和較小的壁厚會使最大壓降處于較高水平,因而實際設計中應避免同時出現壁厚很大與過濾體直徑很小的情況。綜上分析,為實現DPF最大壓降最小化的目標,孔隙率與壁厚需選擇較小,過濾體直徑需選擇較大。

圖11a示出孔隙率與壁厚在其余結構參數為零水平時對初始捕集效率的影響響應曲面。圖11a中,響應曲面的初始捕集效率高值區向大孔隙率大壁厚方向傾斜,表明隨著DPF孔隙率和壁厚的增大,DPF初始捕集效率增大,且壁厚占主導因素,壁厚在0～1水平時,初始捕集效率能保持在一個較高水平,而壁厚與孔隙率取值在零水平以下時,初始捕集效率的等值線變得密集,響應曲面坡度變陡,DPF初始捕集效率顯著下降。因此,選用較大的壁厚有利于提高初始捕集效率。圖11b示出孔隙率與過濾體直徑在其余結構參數為零水平時對初始捕集效率的影響響應曲面。由圖11b可知,隨著DPF孔隙率和過濾體直徑的增大,DPF初始捕集效率增大。另外,響應曲面整體坡度平緩,表明孔隙率與過濾體直徑對初始捕集效率的交互影響相對較弱。圖11c示出壁厚與過濾體直徑在其余結構參數為零水平時對初始捕集效率的影響響應曲面。由圖11c可知,隨著壁厚和過濾體直徑的增加,DPF初始捕集效率增加,壁厚與過濾體直徑取值在零水平以下時,DPF初始捕集效率會顯著下降,為優化初始捕集效率,過濾體直徑與壁厚應盡量避開低水平區域。

綜上分析,DPF采用較大的過濾體直徑配合適中的壁厚和孔隙率才能使最大壓降保持在低值區,初始捕集效率保持在高值區域。

圖11 結構參數對初始捕集效率的交互作用

4 多目標參數優化

4.1 滿意度函數法

綜上分析可知,結構參數對DPF捕集性能的影響較復雜,參數間交互作用顯著,且最大壓降與初始捕集效率之間相互制約。滿意度函數法是一種適合于多目標優化的方法[22],該方法將每個響應面的響應函數yi(i= 1,2,…n)轉換為0～1之間無量綱尺度滿意度函數d(yi),通過求取各響應面d(yi)的幾何平均值將多個單響應滿意度函數轉化為一個復合滿意度函數D,從而實現多響應優化問題轉變為單響應優化問題。

針對響應問題的性質差異,可將其歸類為 3 種情況:望大特性、望小特性和望目特性,相應的滿意度函數如式(13)至式(15)所示。滿意度函數d(yi)隨相應響應值的滿意度增大而增大,d(yi)=0表示響應值不可接受,d(yi)=1表示響應值完全可取。

1) 望大特性,響應值越大越好,相應函數為

(13)

2) 望小特性,響應值越小越好,相應函數為

(14)

3) 望目特性,響應值達到某一期望值時最佳,相應函數為

(15)

式中:i是響應序號;y是響應值;yi是第i個響應的響應值;mi是第i個響應的上限;li是第i個響應的下限;Ti是第i個響應響應值的目標值;r是響應的權重。

對于多響應優化問題,在計算得到單個響應的滿意度函數d(yi)之后,采用幾何平均的思想定義復合滿意度函數D(0≤D≤1),單個滿意度函數轉化為復合滿意度函數計算表達式為

(16)

式中:ωi表示響應的重要程度,各響應權重的總和∑ωi=1。本次優化設定最大壓降權重ω1= 0.5,初始捕集效率權重ω2= 0.5。

4.2 DPF結構參數優化

基于自變量和因變量之間的響應曲面二階回歸方程式(11)和式(12),通過滿意度函數法分別對兩個響應函數進行轉化,由于DPF設計以最大壓降最小化和初始捕集效率最大化作為優化目標,故最大壓降響應滿足望小特性,初始捕集效率響應滿足望大特性,以試驗設計中最大壓降的最小值和初始捕集效率的最大值為目標值,得出最大壓降與初始捕集效率的滿意度函數,見式(17)和式(18)。

(17)

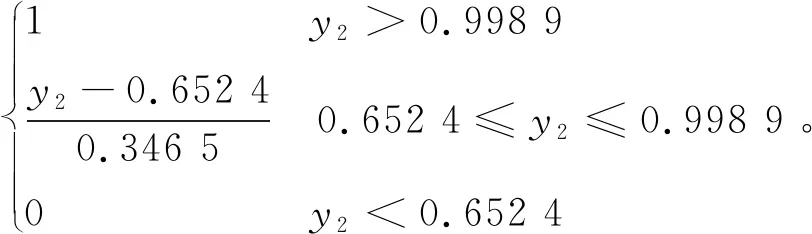
(18)

將式(17)與式(18)代入式(16)中,可得d(y1)與d(y2)的復合滿意度函數D,此復合滿意度函數即為優化的目標函數,利用優化算法對目標函數D進行最大化尋優,從而確定最優解[23]。

(19)

4.3 優化結果及仿真驗證

優化后的結構參數見表8。由表8可見,結構參數最優組合滿意度為0.98,此時最大壓降為3.09 kPa,初始捕集效率為99.89%。孔隙率、壁厚和過濾體直徑在優化范圍內取值適中,微孔直徑取值在下邊界,過濾體直徑取值在上邊界,優化結果與交互作用分析結果相符。

表8 優化結果比較

優化后的DPF壓降曲線和捕集效率曲線見圖12和圖13。初始壓降較優化前下降36.67%,最大壓降較優化前下降51.42%。優化后DPF在整個加載過程中的壓降顯著降低,有利于減緩發動機排氣背壓增加速度、提高發動機燃油經濟性以及減少DPF再生頻率。優化前后的DPF最大捕集效率基本相同,但初始捕集效率有了很大提高,達到了99%以上,這表明優化后DPF在整個加載過程中都能保持較高捕集效率,具有更強的顆粒物攔截能力。因此,優化后的DPF捕集性能明顯優于原始DPF。

圖12 優化前后的壓降對比

圖13 優化前后的捕集效率對比

5 結論

a) 采用響應曲面法建立了DPF捕集過程中最大壓降和初始捕集效率的回歸模型,診斷分析結果表明,響應面擬合結果較好,模型具有較高的精度,可以用來預測DPF最大壓降和初始捕集效率;

b) 孔直徑對最大壓降的影響非常小,孔隙率、過濾體長度、壁厚以及過濾體直徑對最大壓降的影響顯著;5個結構參數對初始捕集效率影響均極顯著;

c) 較小的孔隙率與壁厚、較大的過濾體直徑有利于降低DPF最大壓降,而適當增大過濾體直徑與壁厚可提升DPF初始捕集效率,因此,采用較大的過濾體直徑配合適宜的壁厚和孔隙率有利于提高DPF整體捕集性能;

d) 基于滿意度函數法對DPF結構參數進行多目標優化,優化后的DPF最大壓降較優化前下降51.42%,優化后的DPF初始過濾效率趨近于100%。