基于無位置傳感器的潛航器集成電機推進系統

蘇錦智，張繼鵬，安群濤，王 輝，張偉峰

（1. 包頭長安永磁電機有限公司，內蒙古 包頭 014030；2. 哈爾濱工業大學 電氣工程及自動化學院，黑龍江 哈爾濱 150001；3. 內蒙古自治區先進永磁電機及其控制技術企業重點實驗室，內蒙古 包頭 014030）

0 引言

潛航器無軸推進技術取消了傳統推進系統的傳動軸，將推進電機的轉子和與螺旋槳一體化設計構成了集成電機推進系統，具有噪聲低、體積小、可靠性高的特點，得到了研究與應用[1-2]。永磁同步電機因效率高、功率密度高、控制特性好，在潛航器推進系統中得到廣泛應用[3]。永磁同步電機的高性能運行控制需要檢測轉子位置信息，然而在集成電機推進系統中，傳統推進電機軸系上的位置傳感器極大地增加了水下動密封的難度，給系統的可靠性帶來風險，為此，無位置傳感器控制技術被應用于水下潛航器推進系統[4]。

永磁同步電機無位置傳感器技術可以分為2類：1）基于電機凸極效應的高頻注入法，受信噪比等因素的影響它僅適合于零速和低速階段；2）基于電機基波模型的方法，主要采用觀測器獲取電機反電動勢或磁鏈估計值，進而計算轉子位置和速度。由于反電動勢和磁鏈的幅值與電機轉速成正比，低速下幅值較小導致觀測誤差較大，因此該類方法僅適合于中、高速階段。目前常用的觀測器方法有滑模觀測器（SMO）[5]、龍貝格觀測器[6]、模型參考自適應（MRAS）[7]、擴張狀態觀測器（ESO）[8]、擴展卡爾曼濾波器（EKF）[9]等。與其他方法相比，滑模觀測器具有動態響應快、魯棒性好等優點，得到了研究者的關注[10]。為實現電機的全速域無位置傳感器運行，需要將這類方法相結合。文獻[4]研究了高頻脈振電壓信號注入法和模型參考自適應法相結合的無位置傳感器復合檢測方法，實現了潛航器推進電機的全速域運行。文獻[11]研究了將高頻注入與觀測器相結合的加權切換策略，減小了切換時的力矩擾動。文獻[12]將恒流頻比控制（IF）起動與滑模觀測器結合，通過設計過渡狀態實現了2 種控制策略的平滑切換。

IF 控制是永磁同步電機無位置控制中常用的起動方式，它通過恒電流頻率頻比控制拖動電機運行到一定轉速，從而開啟觀測器算法并過渡到閉環控制的無位置模式。為提升IF 到SMO 的切換速度，減小切換擾動并提高切換的可靠性。本文將IF 控制構建的虛擬dq坐標系與SMO 觀測的dq坐標系相結合，通過dq軸電流的平滑過渡，實現IF 和SMO 之間的無擾切換。將該策略應用于一臺潛航器集成電機推進系統中，實現了電機轉速良好的動態響應。

1 永磁同步電機的矢量控制

1.1 數學模型

永磁同步電機的電壓、電流、反電動勢等變量在abc自然坐標系中為交流量，不利于實現高性能控制，通常結合坐標變換思想，建立永磁同步電機在同步旋轉轉子dq坐標系下的數學模型。在dq坐標系中，各變量變換為直流量，獲取類似于直流電機的控制性能。永磁同步電機在dq坐標下的數學模型描述為

式中：ud、uq和id、iq分別為d、q軸電壓和電流；R為繞組相電阻；Ld、Lq分別為d、q軸電感；ω為轉子電角頻率；ψf為永磁磁鏈；Te為電磁轉矩；np為電機極對數。

1.2 矢量控制系統

對于交、直軸電感相等的表貼式永磁同步電機，電磁轉矩大小與q軸電流成正比，且d軸電流為0 時可以實現最大轉矩電流比控制。采用id=0的永磁同步電機矢量控制系統如圖1 所示，它借助坐標變換將檢測的繞組電流變換到同步旋轉的dq坐標系中，在dq坐標系下分別對d、q軸電流分量進行調節，由于d、q軸的電流為直流量可采用PI調節器實現其無靜差控制。與基于機械轉子位置傳感器的矢量控制不同的是，這里電機轉子的位置和速度信息通過SMO 和反正切計算構成的位置和速度估算單元獲取，從而取代了傳統通過位置傳感器檢測的方案。SMO 建立在兩相靜止的αβ坐標系下，根據電機的α、β軸電壓和電流觀測得到電機的反電動勢估計值e?α和e?β，將其送入到反正切計算單元得到位置估算值θ? 和速度估算值ω?，用于矢量解耦和閉環反饋。

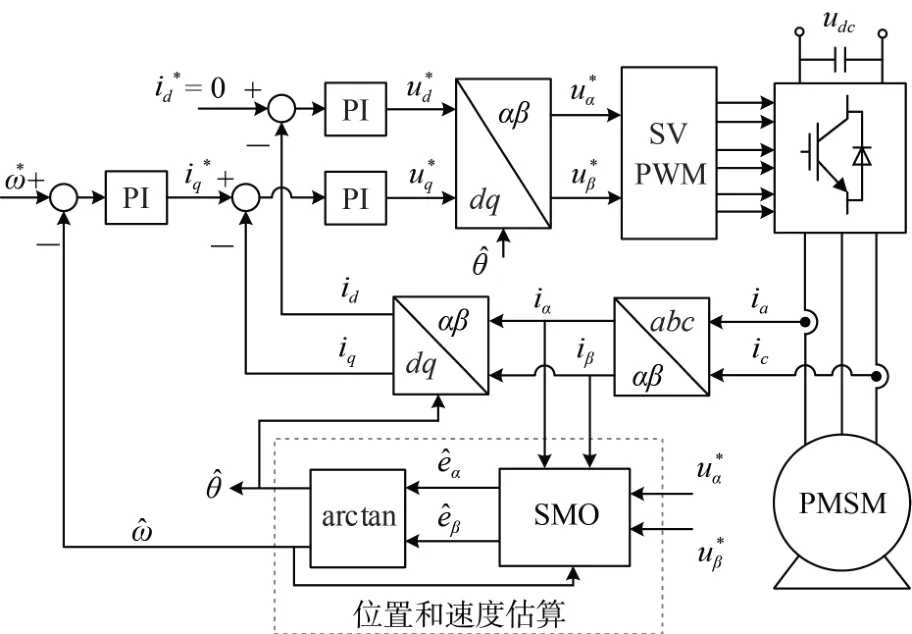
圖1 永磁同步電機無位置傳感器矢量控制系統Fig. 1 Sensorless vector control of PMSM

在無位置傳感器控制系統中，轉子位置和速度獲取的響應和精度直接影響到電機的性能甚至穩定性，且在電機運行的全速范圍內，電機從零速起動，需要結合低速運行的IF 策略，并在轉速到達一定值后切換至SMO 模式。同樣地，當電機由高速減速到低速運行或停機時，則需要由SMO 模式切換至IF 模式。

2 基于滑模觀測器的位置和速度估算

2.1 滑模觀測器

根據永磁同步電機的數學模型可以構建αβ坐標系下的狀態方程為

式中：eα、eβ、iα、iβ、uα、uβ分別為電機α、β軸的反電動勢、電流和電壓；L為繞組電感，對于隱極電機有Ld=Lq=L。這里的反電動勢為轉速ω和位置θ的函數，即

根據式（2）可以構建電流狀態觀測模型為

式中：“?”表示變量的估算值；zα和zβ為滑模切換函數，通常采用如下符號函數：

式中：sgn（）表示符號函數；k為增益，為保證觀測器穩定，取分別為α、β軸的電流誤差。將式（4）代入到式（2）中，得到SMO 的狀態誤差方程為

在控制量zα和zβ的調節下系統收斂，上式的α、β軸電流誤差趨于0，這樣電機的反電勢可由控制量zα、zβ進行低通濾波后得到，即滑模觀測器估算αβ軸反電勢為

式中：ωc為低通濾波器的截至頻率，濾波后的反電勢包含電機的轉速與位置信息，可以按如下公式進行求取：

滑模觀測器的結構框圖如圖2 所示。

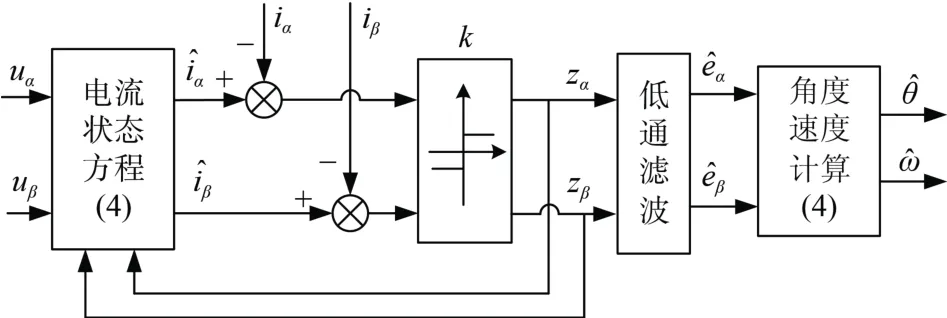
圖2 滑模觀測器結構框圖Fig. 2 Diagram of the SMO

2.2 起動與切換策略

電機起動時轉速和反電動勢均為0，無法通過觀測器獲取轉子位置，可以通過恒流頻比的IF 控制拖動電機起動。IF 控制下，電機轉子角度由控制器給定，且頻率逐步提升。在電流iq*的拖動下，電機逐步旋轉起來，給定坐標系d*q*將超前于實際坐標系dq一個負載角Δθ，如圖3 所示，電機的力矩為

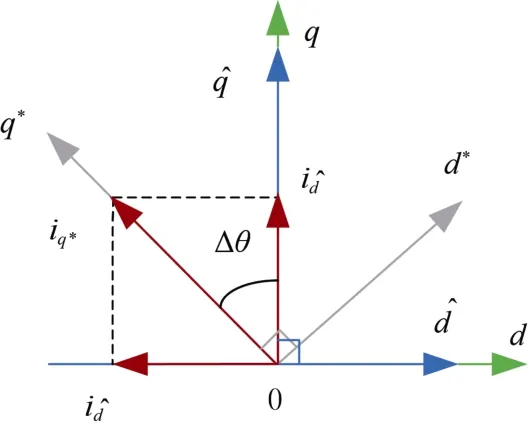
圖3 IF 坐標系與觀測坐標系之間的關系Fig. 3 Relationship between IF coordinate system and observing coordinate system

為實現永磁同步電機全速閾范圍內的無位置傳感器控制，需要實現IF 控制與SMO 雙閉環控制之間切換。在狀態切換過程中，電機可能會切換策略不當、切換過程中負載擾動等因素導致電機失步。常見的加權函數狀態切換法能改善切換時的轉矩和轉速擾動，但對負載的適應性較差。基于功角自平衡原理逐步減小電流幅值的切換策略對負載的適應性較好，但快速性較差且容易因為負載擾動導致電機失步。

下面介紹在雙dq坐標系實現的狀態切換策略。電機起動到一定轉速后，SMO 可以準確估算出轉子的位置，這樣SMO 估算坐標系與實際坐標系dq重合。在IF 控制下，由于d*q*坐標系與dq坐標系之間存在角度差Δθ，由IF 控制直接切換到轉速閉環模式時，將產生較大的擾動且容易出現失步。為提高切換的穩定性、加快響應，d*q*的電流指令賦值給d?q? 坐標系中，使切換前后電流矢量的大小和方向均保持不變，即

3 實驗結果

設計1 kW 集成電機推進系統，并對本文所采用的無位置控制算法和切換策略進行驗證。電機額定轉速為1 200 r/min，額定轉矩為8 N·m，系統供電電壓為270 V。控制器采用TMS320F28335 作為主控芯片，逆變器選用集成功率模塊（IPM），開關頻率為10 kHz。

電機軸上分別施加5 N·m 和8 N·m 負載力矩，采用傳統減小電流矢量幅值切換策略的位置波形分別如圖4 和圖5 所示。在5 N·m 負載力矩下電機由IF 切換至SMO 過程中，轉速出現大幅跌落后能夠逐步穩定到SMO 模式運行，并且在多次測試中偶爾會出現切換失敗導致電機失步現象。在8 N·m 負載力矩下，IF 至SMO 切換過程中電機頻繁出現失步停機，并且多次實驗表明，電機所帶負載越大失步的概率越高。上述實驗表明：IF 與SMO 之間切換過程中，切換策略的選取影響到電機的帶載能力，決定了電機對負載擾動的抵抗性能。傳統通過逐步減小電流使負載角趨于零時進行切換的策略存在易受負載擾動影響，切換時間較長的問題。

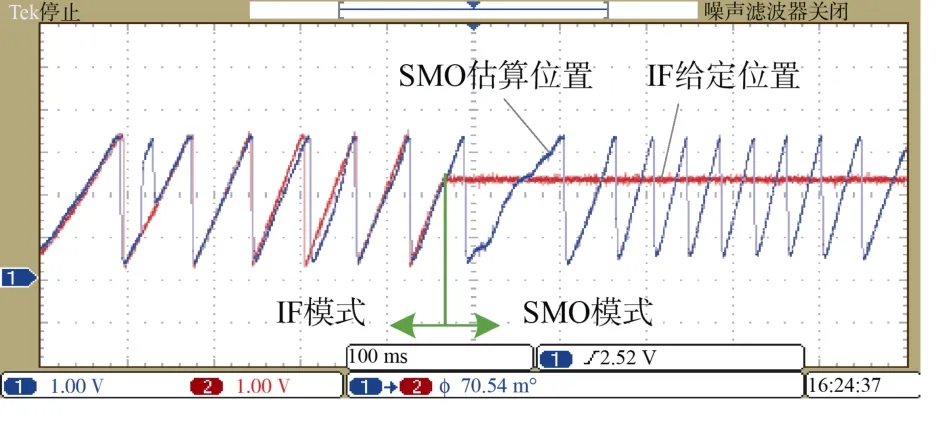
圖4 切換過程中的轉速擾動Fig. 4 Speed disturbance when switching from IF to SMO

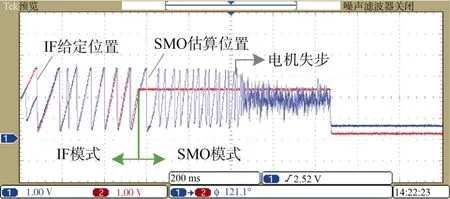
圖5 切換過程中的失步Fig. 5 The motor is out of step when switching from IF to SMO

圖6 為采用本文所述的雙dq坐標系切換策略的實驗結果，電機帶額定的8 N·m 負載起動，由IF 至SMO 模式可以平滑切換，切換前后轉速平穩無擾動，并且多次測試中電機均能快速平滑地起動和穩定運行。對集成電機推進系統進行水下起動和正反轉測試，測試結果表明：采用本文所設計的算法電機表現出良好的動態特性和穩定性，滿足潛航器對集成電機推進系統的要求。

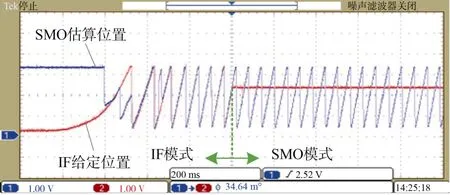
圖6 雙dq 坐標系下的平滑切換Fig. 6 Smooth switching under the double dq frames

基于該算法開發的集成推進電機系統已應用于潛航器中，經過4 年左右的充分驗證，表明了該算法可靠性高、性能穩定。

4 結束語

采用無位置傳感器控制永磁同步電機的潛航器集成電機推進系統具有體積小、效率高、可靠性高等優點。本文設計了基于滑模觀測器的永磁同步電機無位置控制系統，通過對電機起動過程的研究，低速段采用IF 控制，高速段為SMO 無位置控制，采用雙dq坐標系的切換策略實現了IF 控制和SMO 控制的無擾切換，提升了系統運行的穩定性和快速性。測試結果驗證了該系統具有良好的綜合性能，能夠滿足潛航器垂推系統的需求。