一種混合社會群體優化算法

王也 曲會晨 林奕森

摘要：為了提高社會群體優化算法的整體性能，提出一種混合社會群體優化算法。在提高階段，通過對最差個體進行反向學習，提高種群的搜索空間，從而使得種群整體能夠快速的向最優解收斂；在獲得階段，通過Logistic映射產生混沌擾動，增大種群的多樣性，從而能夠增加算法跳出局部最優解的可能性。基于標準測試函數的實驗研究結果表明改進算法整體提升了尋優效果。

關鍵詞：社會群體優化算法；反向學習；混沌搜索；Logistic映射；優化

中圖分類號：TP301.6? ? ?文獻標識碼：A

文章編號：1009-3044（2023）06-0047-04

開放科學（資源服務）標識碼（OSID）

0 引言

社會群體優化算法（Social Group Optimization，SGO）在2016年，由學者Satapathy等人[1]提出的一種新興群智能優化算法，該算法通過模擬社會成員在社會群體中學習能力和知識的過程，實現社會群體整體能力的提升。該算法與目前現有的優化算法相比，結構簡單易懂、設置參數較少，對處理一些函數優化問題效果較好，Satapathy等人[1]證明了SGO算法在整體性能上優于TLBO算法和GA、PSO、DE、ABC算法及改進算法。Anima Naik等人[2]通過將SGO算法與8種PSO改進算法對比，證明了SGO算法具有較好的解決多模態和數據聚類問題。劉亞軍[3]等人通過將量子學習和多子群學習方法共同引入到SGO算法中，提出了基于多子群社會群體學習算法（MPSGO），并與目前熱門的TLBO算法及其改進算法進行了比較，證明了其改進算法的有效性。

在算法應用方面，Jiake Fang等人[4]提出了一種改進型社會群體優化算法（ISGO），并將該算法用于變壓器故障診斷中。SGO算法目前已經還被應用到求解涂抹加強筋法的解析解[5]、腦MRI缺血性腦損傷分割[6]、皮膚黑色素瘤圖像評價[7]、云環境資源有效配置與任務調度[8]等眾多領域中，并取得良好的效果。

綜上所述，雖然SGO算法從提出之日起就廣受學者的歡迎，被廣泛應用，并且也提出了一些改進算法，但是該算法在搜索最優解的過程中，算法的收斂精度和穩定性還有待提升。為此，本文提出一種混合社會群體優化算法（Hybrid Improved Social Group Optimization，HISGO）算法來提升算法的整體性能。

在提高階段，通過加入反向學習機制，擴大了種群搜索最優解的范圍，使得算法能夠快速收斂。在獲得階段，通過加入Logistic映射，使種群產生擾動策略，從而防止種群因多樣性丟失，而陷入局部最優。仿真實驗表明，本文提出的算法在算法收斂精度和穩定性方面都有明顯提升。

1 社會群體優化算法

基本的社會群體算法的主要步驟分為提高階段和獲得階段兩部分。

1.1 提高階段

在社會群體優化算法的提高階段，社會群體成員以最優個體作為學習對象進行學習和提高。該階段所產生的新個體按照式（1）產生。

[Xnewj i=c*Xoldji+r*（Xjbest-Xoldji）]? ? ? ? ? ? ? ? ? ?（1）

式中：c通常取值為0～1的隨機數，代表每個個體在提高階段自我反省系數，根據文獻[1]可知，其在c取值為0.2時，算法效果達到最佳；r為0～1間的隨機數；n和m分別表示種群個數和維數，[j=1，2，...，n，i=1，2，...，m;Xjbest]為目前種群中最優個體的第j維向量；[Xoldji]表示第i個個體第j維向量還未進行提高階段的值；[Xnewj i]表示進行完提高階段第i個個體第j維向量。社會群體成員[Xi]的能力值是否獲得提升，通過適應度值[函數f（Xi）]來做評判標準；以最大化為標準下，如果[f（Xnewi）]大于[f（Xoldi）]表示社會群體成員[Xi]在經歷提高階段后，其能力值獲得提升，則用[Xnewi]更新[Xoldi]，否則不更新個體，保留[Xoldi]。

1.2 獲得階段

在社會群體優化算法的獲得階段，社會群體成員，通過目前種群中最優個體的引導，與社會群體其他成員之間進行相互交流學習的方式進行能力的獲得和提升。該階段所產生新個體按照式（2）產生。

[Xnewj i=Xoldji+r1*Xjbest-Xoldji+r2*Xoldjk-Xoldji? ? ? ? fXoldk>fXoldi Xoldji+r1*Xjbest-Xoldji+r2*Xoldji-Xoldjk? ? ? ?fXoldi>fXoldk]? ?（2）

式中：[r1]和[r2]為0～1的隨機數；[Xoldji]和[Xoldjk]分別為未進行獲得階段的第i和第k個個體的第j維向量；[Xjbest]為目前種群中最優個體的第j維向量；[Xnewj i]表示進行完獲得階段第i個個體第j維向量。社會群體成員[Xi]的能力值是否獲得提升，通過適應度值[函數f（Xi）]來做評判標準；以最大化為標準下，如果[f（Xnewi）]大于[f（Xoldi）]，表示社會群體成員[Xi]在經歷獲得階段后，其能力值獲得提升，則用[Xnewi]更新[Xoldi]，否則不更新個體，保留[Xoldi]。

2 HISGO

社會群體優化算法存在設置參數較少、結構簡單易懂、收斂能力強等優點；但根據文獻[1-4]的仿真實驗結果可知，算法還存在收斂精度、已陷入局部最優解等問題。為此本文通過在算法的提高階段和獲得階段，分別加入反向學習機制和Logistic映射產生的混沌搜索，來擴大最優解的搜索范圍，并保持算法的種群多樣性，避免算法陷入局部最優解，提升算法的精度和穩定性。從而整體上使社會群體優化算法的性能獲得提升。

2.1 反向學習策略

反向學習（Opposition-Based Learning， OBL）是Tizhoosh [9] 于2005年提出了一種通過同時比較當前解和其反向解，并從中擇優選擇的一種策略[9]。

假設n維空間上一個解[X=（x1，x2，...，xn）]，并且[x1，x2，...，xn∈R，xi∈[ai，bi]]，則解X的反向解[X*=（x*1，x*2，...，x*n）]，可由式（3）獲得。

[x*i=ai+bi-xi]? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （3）

為保證社會群體優化算法種群的整體性能，提高搜索空間，在算法提高階段更新種群后，根據式（3）對種群最差個體進行反向學習，產生反向學習個體，并用反向學習個體替代最差個體，從而擴大搜索最優解的范圍，提升算法搜索到最優解的可能性。

2.2 混沌搜索

在社會群體優化算法搜索最優解的過程中，存在陷入局部最優解的現象。在算法尋優的過程中，通過增加種群的多樣性的方式，有利于算法跳出局部最優解[10]。為此，本文通過產生相應的隨機解的方式，對種群進行擾動，從而達到增加種群的多樣性的目的，增加算法跳出局部最優解的可能性。

本文采用Logistic映射產生混沌序列來對種群進行擾動。Logistic映射公式如式（4）所示。

[zk+1=μzk（1-zk）]? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

式中：[ k=1，2，...，n]表示混沌的序列的序列號，[zk]為區間（0，1）上的數，混沌序列z的第k+1個個體用[zk+1]表示，[μ]是可調參數，取值范圍為[0，4]。

2.3 算法實現流程

綜上所述，本文提出的HISGO算法的具體實現步驟如下：

步驟一：初始化，設置社會群體中社會成員人數即種群個體數目m，社會成員需提升的能力個數即種群的維度n，算法最大迭代次數[Tmax]，并產生[m×n]的初始種群；

步驟二：按照式（1）產生經過提高階段后的新個體，并計算適應度值，當新個體適應度值優于舊個體時，則用新個體更新舊個體，反之不更新個體；

步驟三：對提高階段進行更新后的個體，按照式（3）對最差個體進行反向學習，產生相對應的反向學習個體，用反向個體替代最差個體；

步驟四：按照式（2）產生經過獲得階段后的新個體，并計算適應度值，當新個體適應度值優于舊個體時，則用新個體更新舊個體，反之不更新個體；

步驟五：對獲得階段進行更新后的個體，按照式（4）進行Logistic映射擾動，產生相對應的擾動個體，并計算適應度值，當新個體（擾動個體）適應度值優于舊個體時，則用新個體更新舊個體，反之不更新個體；

步驟六：直到滿足終止條件為止（一般為滿足算法最大迭代次數[Tmax]），算法結束，并輸出當前最優個體。

3 實驗仿真與結果分析

為驗證本文提出的改進算法的整體性能，選取CEC2005測試函數集中[10]9個標準函數作為測試函數，對算法的整體性能進行驗證，并與SGO算法[1-2]、目前SGO算法改進效果較好的MPSGO算法[3]和ISGO算法[4]，進行對比。

3.1 測試函數選取

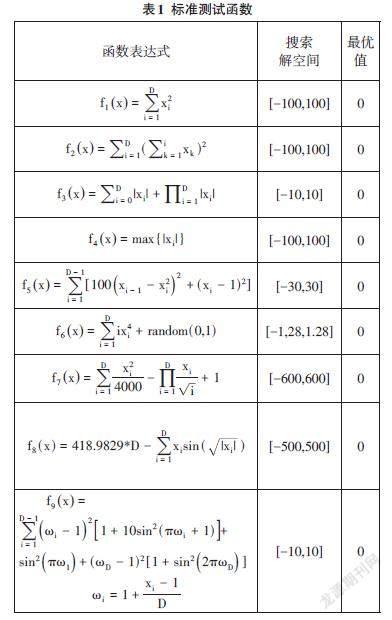
本文所選取測試函數的表達式、取值范圍和理論最優值如表1所示。

在表1中，D表示待優化的函數的決策變量的維數，設置維數D為30進行實驗。本文仿真實驗在Intel（Ｒ） Core（TM） i7-8550U CPU@1.8GHZ，8G內存，操作系統為window10家庭版的計算機上進行，仿真軟件環境為Matlab 2018a。

3.2 算法實驗結果與分析

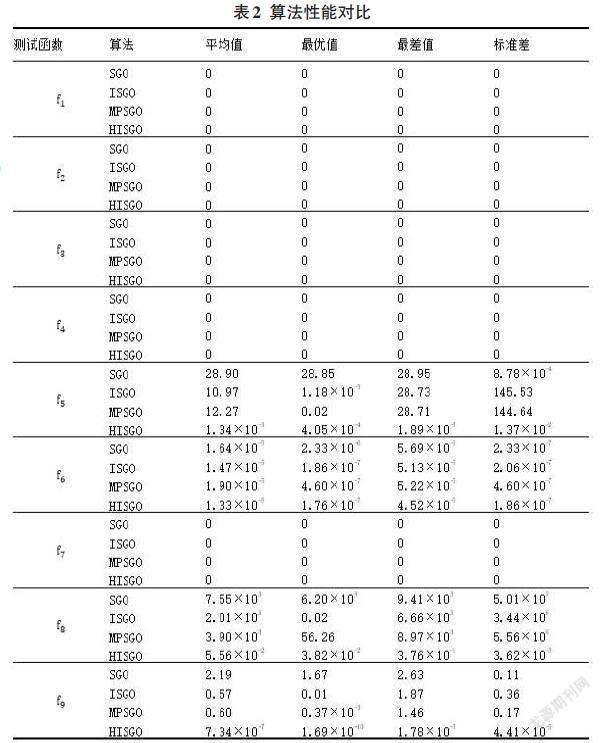
為了驗證本文算法的有效性，通過對比每個算法的平局值、最優值、最差值、方差來驗證算法的性能，并且為了避免特殊情況的影響，本文每種算法對于每一個測試函數都獨立運行30次。算法的性能對比如表2所示。

從表2可以看出，本文提出的HISGO算法在總共9個測試函數中與對比算法進行測試，對于測試函數[f1～f4]和[f7]，4種算法都能收斂到測試函數的理論最優值0，表明在3個對比算法已經能夠獲得理論最優值的情況下，HISGO算法能夠保持原有的收斂精度。

對于測試函數[f5]、[f6]、[f8和f9]，HISGO算法和3個對比算法未能收斂到理論最優值0。但從平均值、最優值和最差值3方面上看，本文的HISGO算法都優于3個對比算法，并且除了測試函數[f6]以外，HISGO算法獲得的最差值都要遠遠優于其他3種算法的最優值，因此可以得出，本文提出的HISGO算法在收斂精度上，對于現有的SGO及其改進算法MPSGO和ISGO，都獲得了較大的提升。方差上看，HISGO算法也要遠優于其他3個對比算法，尤其是測試函數[f5]、[f8和f9]，相對于3種對比算法都要高出數十幾個數量級，這也進一步證明了本文算法在穩定性方面，對于現有算法存在穩定性差的方面進行了較大幅度的提升。

4 結束語

本文基于反向學習策略和Logistic映射混沌擾動思想，在SGO算法的提高階段結束后，將最差個體進行反向學習，在獲得階段結束后加入Logistic映射對種群進行擾動，提出了HISGO算法。通過將本文算法與3個對比算法在典型標準測試函數上進行測試表明，通過加入反向學習策略，增大了最優解搜索空間，使得本文算法相對于對比算法具有較好的收斂精度；通過加入混沌擾動策略，增加了種群的多樣性，使得本文算法相對于對比算法具有較好的收斂精度和穩定性；從而整體提升了算法的性能。

參考文獻：

[2] Naik A，Satapathy S C，Ashour A S，et al.Social group optimization for global optimization of multimodal functions and data clustering problems[J].Neural Computing and Applications，2018，30（1）：271-287.

[1] Satapathy S，Naik A.Social group optimization （SGO）：a new population evolutionary optimization technique[J].Complex & Intelligent Systems，2016，2（3）：173-203.

[2] Naik A，Satapathy S C，Ashour A S，et al.Social group optimization for global optimization of multimodal functions and data clustering problems[J].Neural Computing and Applications，2018，30（1）：271-287.

[3] 劉亞軍，陳得寶，鄒鋒，等.基于多子群的社會群體優化算法[J].計算機應用研究，2019，36（5）：80-85.

[4] Fang J K，Zheng H B，Liu J F，et al.A transformer fault diagnosis model using an optimal hybrid dissolved gas analysis features subset with improved social group optimization-support vector machine classifier[J].Energies，2018，11（8）：1922.

[5] Minh-Tu.Optimisation of stiffeners for maximum fundamental frequency of cross-ply laminated cylindrical panels using social group optimisation and smeared stiffener method[J].Thin-Walled Structures，2017，120：172-179.

[6] Rajinikanth V，Satapathy S C.Segmentation of ischemic stroke lesion in brain MRI based on social group optimization and fuzzy-tsallis entropy[J].Arabian Journal for Science and Engineering，2018，43（8）：4365-4378.

[7] Dey N，Rajinikanth V，Ashour A，et al.Social group optimization supported segmentation and evaluation of skin melanoma images[J].Symmetry，2018，10（2）：51.

[8]，Janakiramaiah B.Effective allocation of resources and task scheduling in cloud environment using social group optimization[J].Arabian Journal for Science and Engineering，2018，43（8）：4265-4272.

[9] Tizhoosh H R.Opposition-based learning：a new scheme for machine intelligence[C]//International Conference on Computational Intelligence for Modelling，Control and Automation and International Conference on Intelligent Agents，Web Technologies and Internet Commerce （CIMCA-IAWTIC'06）.November 28-30，2005，Vienna，Austria.IEEE，2006：695-701.

[10] 肖婧，許小可，張永建.差分進化算法及其高維多目標優化應用[M].北京：人民郵電出版社，2018：31-32.

【通聯編輯：謝媛媛】