基于CS 的帶時間窗多技能人力資源路徑優化

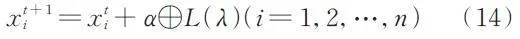
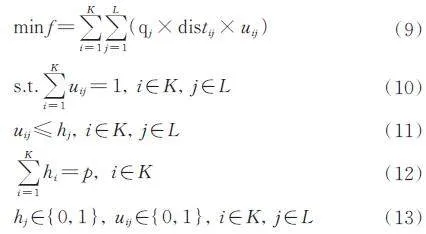
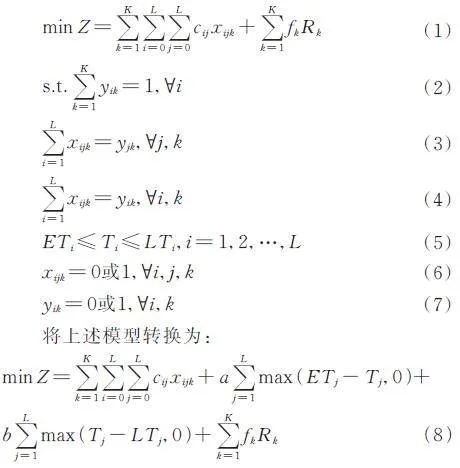
摘 要：針對帶時間窗多技能人力資源路徑優化問題，分別構建了兩種數學模型，利用改進的布谷鳥搜索算法（Cuckoo Search Algorithm， CS）對模型進行求解。求出不同類型客戶群企業或組織的運作成本，并對模型的適用性進行了討論，對密集型客戶適合模型Ⅱ，即先分區后指派；對分散型客戶適合模型Ⅰ，即直接指派。該研究可為企業或組織的決策提供參考，為員工的招聘和安排提供理論指導。

關鍵詞：布谷鳥搜索算法；人力資源路徑優化；時間窗；多技能

中圖分類號： TP3 文獻標識碼： A 文章編號： 1673-8462（2023）03-0086-05

0 引言

隨著勞動力數量和質量的雙變導致企業用工成本增加，給企業的經營管理帶來巨大壓力。具備多技能的員工能適應多種工作崗位，使企業的人員安排更加靈活，能有效降低企業的人力成本，因此，在企業實踐管理中，多技能員工越來越受到企業的青睞。然而，在不同技能員工的工作安排中涉及多個任務，每個任務有時間窗要求和所需不同技能，如何合理安排不同技能員工的工作任務，使企業的運作成本最低，成為企業亟待解決的問題。

近年來，不少專家學者對人力資源管理從不同角度進行研究，袁方潔等人［1］提出基于多階段遺傳算法的人力資源管理，針對企業員工雇傭計劃的優化問題建立數學模型，通過合理控制不同時段解聘數量來提高雇員的平均工作能力，從而實現項目的人力資源優化。李明等人［2-3］分別提出基于均衡優化的項目多技能人力資源指派與調度方法和項目多技能人力資源指派與調度混合算法，其在文獻［2］中首先采用啟發式方法對項目進行資源均衡化并建立整數規劃模型，通過編程計算驗證了可以有效降低項目人力資源成本，在文獻［3］中將原問題分為指派問題和調度問題構建模型，編程實現提高多技能人力資源的使用率。康麗等人［4］提出基于時間窗的家庭醫療護理人力資源分配，其在資源分配階段考慮時間窗約束和所提出的層次優化算法，實驗結果驗證了模型的有效性。王一凡等人［5］提出求解多技能人力資源約束的項目調度問題的兩階段算法，實驗結果顯示其是一種有效方法。段鵬飛等人［6］提出求解廣義優先關系下多技能人員項目調度問題的改進布谷鳥搜索算法，實驗結果表明其是一種有效方法。李松等人［7］提出人力資源調度的蟻群算法模型，實例證明該算法能有效節省人力資源成本。沈國軍等人［8］提出基于改進遺傳算法的人力資源指派模型，簡化了人力資源指派流程，產生較好的項目績效。伊雅麗等人［9］提出基于蟻群算法求解研發型多項目人力資源調度研究，為人力資源調度方案提供了新的解決途徑。但鮮有研究將時間窗與多技能約束統籌考慮，雖然文獻［10］將兩者綜合考慮，但未對客戶類型進行細分研究。本文根據現實管理需求，建立兩種數學模型分別用CS 算法求解，通過六種不同類型客戶群的仿真實驗，針對不同類型客戶群適合哪種數學模型企業的運作成本最小給出了理論指導。

1 問題描述與數學模型

1.1 問題描述

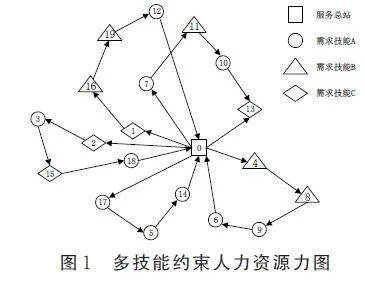
在企業或管理者安排技術人員服務客戶時，多個客戶在地理位置上的分布一般較為不同，在同一時間內，不同客戶所提需求也不盡相同，從而構成一個復雜的服務網絡。本文以帶時間窗的多技能約束服務網絡為研究對象，網絡由一個服務總站，若干個客戶節點構成，如圖1 所示。服務總站即圖中編號為0的節點，由其派遣多個專業技術人員為不同需求的客戶進行服務，每個技術人員從服務總站出發，完成任務后返回出發點；每個客戶具有需求技能約束和時間窗約束，在圖1 中分別用不同形狀進行表示。對管理者而言，如何合理安排各種專業技術人員在滿足各客戶技能約束和時間窗約束的基礎上，使組織的運作成本最小化。

1.2 數學模型Ⅰ

假設服務總站需派遣K （ k = 1，2，…，K ） 名技術人員服務L （ i = 1，2，…，L ） 個客戶，每個客戶的服務時間為si （ i = 1，2，…，L ），客戶i 到客戶j 的路徑成本為cij、行程時間為tij （ i，j = 0，1，2，…，L ），技術人員到達客戶i 的時間為Ti（ i = 1，2，…，L ），客戶i 的服務時間窗約束為[ ETi，LTi ]，技術人員的工資成本為f（k 不同技術人員工資標準參見表1），每個技術人員所服務的客戶數為Rk，顯然，在成本結構上，除了路徑成本以外，還有人員工資成本、時間約束懲罰成本。其數學模型如下：

式（1）表示目標函數，式（2）～式（4）表示每個客戶只能被一名技術人員服務，式（5）表示時間窗約束，式（6）～式（7）表示0-1 變量，式（8）中的a，b 分別表示早晚到懲罰系數。

1.3 數學模型Ⅱ

由于客戶地理位置分布不同，通常的做法是將地理位置較近的客戶劃分為一個片區，然后再安排相關的技術人員對其進行服務。假設L 個客戶需要劃分K 個片區，使得K 個片區總距離最短及所需技能最少，每個客戶的技能需求為qi，每個客戶只能由一名技術人員服務，假設服務總站的技術人員足以滿足客戶群的技能需求。因此片區劃分數學模型為：

式（9）表示片區劃分的目標函數，distij 表示客戶i與客戶j 之間的距離，uij 為1 時表示第j 個客戶由第i名技術人員服務，式（10）～式（13）為約束條件。

2 算法設計

2.1 布谷鳥搜索算法

布谷鳥搜索算法（Cuckoo Search Algorithm，CS）由Yang 于2010 年提出，［11］該算法模擬布谷鳥尋窩產卵的過程來求解連續優化問題，其位置更新公式為：

式（14）中xti 表示第i 鳥巢在第t 的位置，α 表示步長控制量，一般取值為0.01；⊕ 表示點乘，L （ λ ） 為Levy 飛行的搜索路徑，且L～u = t-λ，（ 1 lt; λ ≤ 3 ）。位置更新并評價目標函數后，用隨機數r ∈ [ 0，1 ] 與棄巢概率pa 比較，如果r gt; pa，則對xt + 1i 位置隨機改變，否則不變。最后保留最優鳥巢。

2.2 布谷鳥搜索算法離散化

顯然基本布谷鳥搜索算法不能直接求解離散優化問題，因此，采用文獻［12］的方式將其離散化，現假設最優解best＝［2 8 3 5 4 6 7 1］，第i 個Customer＝［2 1 8 3 5 7 4 6］，隨機產生num、Length∈ [ 1，8 ] 之間的兩個整數，比如num＝3，Length＝4，即將Cus?tomer 的值從第3 個位置開始取長度為4 的元素變換成最優解best 一致，變換后的Customer'＝［2 1 3 5 46 8 7］，通過這種隨機選擇位置和改變長度的方式趨向最優解。

2.3 編碼與解碼

編碼是智能算法求解問題的關鍵，它影響著算法的求解性能與效率，本文采用自然數的編碼方式。以圖1 為例，即需求技能r=3，則相應的技術人員按表1 分為2r - 1=7 種類型：

那么，對一個有L 個客戶的帶時間窗多技能人力資源問題，設計雙倍L 編碼：假設客戶編號為Cus?tomer，技術人員編號為Staff。則圖1 所示的一個可行解可以表示為：

Customer：1，7，17，2，16，4，11，5，3，19，15，8，10，14，12，9，18，13，6。

Staff：1，2，4，5，1，3，2，4，5，1，5，3，2，4，1，3，5，2，3

其解碼過程為：

員工1：0–1–16–19–12–0

員工2：0–7–11–10–13–0

員工3：0–4–8–9–6–0

員工4：0–17–5–14–0

員工5：0–2–3–15–18–0

2.4 遺傳算法操作

由于本文算法采用雙倍體編碼方式，遺傳算法不能直接作用于客戶Customer 編碼上，如果這樣在交叉過程中會產生重復客戶編號，因此，將其作用于技術人員Staff 編碼方式上，這樣既可以減少客戶重復編碼的處理又可以改變技術人員服務不同的客戶。同時在遺傳算法的選擇、交叉和變異過程中均采用精英保留策略。

2.5 CS 算法求解步驟

（1） CS 算法求解帶時間窗多技能人力資源路徑優化問題的實施步驟如下（簡稱算法1）。

Step1：參數初始化：種群規模n、棄巢概率pa ，交叉概率pc，最大迭代次數Iter max，遺傳算法迭代次數ga_num、計劃安排人數k 和導入客戶信息等數據。

Step2：按2.3 節介紹的編碼方式隨機產生客戶編號和員工編號，并按式（8）計算每個鳥巢的目標函數值，求出最優值及最優解。

Step3：判斷迭代次數是否達到最大迭代次數，如果是，則退出循環，輸出結果；否則進入Step4。

Step4：執行離散布谷鳥搜索位置的更新，評價此時最優值與最優解；如果隨機數r gt; pa，則對xt + 1i 位置隨機改變，再評價此時最優值與最優解，然后再執行一定次數遺傳算法操作并評價此時最優值與最優解。

Step5：判斷若此時最優值較Step2 中的最優值優越，則替換最優值和最優解，算法進入Step3。

（2） CS 算法求解客戶片區劃分（簡稱算法2）。

算法2 的片區劃分的求解過程，只需要改變算法1 的編碼方式，采用文獻［13］編碼方式（其過程在此不再贅述），目標函數值的計算采用式（9）即可，其余操作與算法1 相同。

（3） CS 算法求解片區內客戶順序（簡稱算法3）。

將算法2 計算的片區劃分結果作為算法3 的輸入，其編碼方式依然采用自然數編碼，目標函數值的計算采用式（8），其余操作與算法1 相同。

3 仿真實驗與分析

為了將兩種不同數學模型+算法設計對企業所產生的成本進行對比。由于本文所研究內容業界尚缺乏標準的數據庫，故采用Solomn 提出的算例庫，其中包含C1、C2、R1、R2、RC1、RC2 六種類型，其中C類表示客戶位置是聚集分布的，R 類表示客戶位置是隨機分布的，RC 類表示客戶位置是混合分布的。另外，又將C，R，RC 類分為1 類和2 類：1 類表示客戶所處范圍較小，2 類表示客戶所處范圍較大。每種類型均包含服務總站、客戶坐標、服務時間、貨物需求量和時間窗。所不同的是將貨物需求量改為客戶所需技能種類，技能種類在［1，3］之間隨機生成，其余不變。

所有的實驗均運行在操作系統為Win10，處理器為Intel（R） i6-6750H CPU， 2.60 GHZ 、內存為8 G的PC 上，采用Matlab R2010a 編程。參數設置見表2所示，由于本文算法是啟發式算法，無法保證每次運行結果一致，故取其運行30 次結果中最好的一次進行分析。所有實驗假設安排10 名技術人員進行服務。

3.1 C201 客戶類型測試

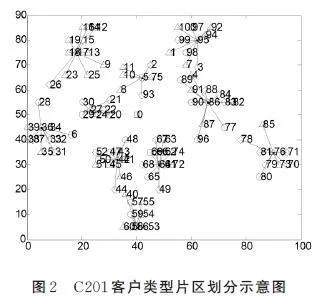
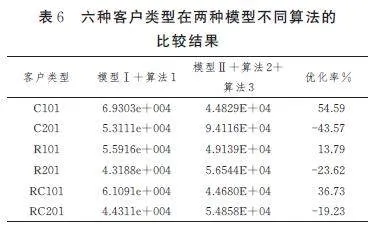
對C201 客戶類型進行實例演算并詳細分析，先展示數學模型Ⅱ+算法2 的計算結果，片區的劃分結果如表3 所示，片區劃分示意圖如圖2 所示。采用算法3 優化客戶順序及所支出成本結果如表4 所示。

再展示數學模型Ⅰ+算法1 的運行結果，計算結果如表5 所示。

對客戶位置較分散的C201 客戶類型來說，從表4 和表5 可得出如下結論：

（1） 如果先分區再指派相應的技術人員進行片區服務與數學模型Ⅰ+算法1 求解結果比較可知，企業或組織所承擔的費用需多支出4.1E+04。

（2） 從表3 可知，盡管將距離較近的客戶劃分成一個片區再由技術人員進行服務，僅考慮了距離成本及所需技能，既沒有考慮技能需求的差異，也要求員工全部掌握3 種技能；而從表5 可知，各種技術人員的合理搭配比單純的路徑優化重要，一組合理的人員搭配可以大大減少企業的運作成本。因此在實踐管理中，不同種類的多技能員工合理搭配可以使企業員工調度更加靈活，并有效降低生產成本。

（3） 從表5 可知，在服務范圍和路徑順序不變的情況下，若全部派遣7 類人員則企業需要多支出的費用。

3.2 其他客戶類型測試

上述僅對一種客戶類型進行實驗演算，下面對其他五種類型進行同樣實驗，計算結果如表6 所示。

從表6 可知，對地理位置分布較小的客戶群C101、R101 和RC101 來說，模型Ⅰ + 算法設計所求成本高于模型Ⅱ + 算法設計；即該類客戶群適用于先分區后指派員工，即適合采用模型Ⅱ+算法2+算法3，由于客戶所處位置分布較小，優化距離比優化多技能員工的合理搭配效果更明顯。而對地理位置分布較大的客戶群C201、R201 和RC201 來說，模型Ⅰ + 算法設計所求成本低于模型Ⅱ + 算法設計；即該類客戶群適合采用模型Ⅰ+算法1，而且越分散優化效果越好，多技能員工的合理搭配效果顯著。因此，對不同類型客戶群需采用不同數學模型和算法進行求解，可以有效降低企業運作成本。

4 結 語

本文利用改進的布谷鳥搜索算法求解帶時間窗的多技能人力資源路徑優化問題，考慮了路徑成本、人力成本、等待成本和延誤成本，更加符合實際情況。通過六種不同類型客戶群，驗證了模型的有效性。同時對模型的適用性進行了討論，對密集型客戶適合模型Ⅱ，即先分區后指派；對分散型客戶適合模型Ⅰ，即直接指派。該研究可為企業或組織的決策提供參考，為員工的招聘和安排提供理論指導。

［參考文獻］

[1] 袁方潔，張佳萍. 基于多階段遺傳算法的人力資源管理[J].云南民族大學學報（自然科學版），2016，25（3）：275-279.

[2] 李明，徐哲. 基于均衡優化的項目多技能人力資源指派與調度方法[J]. 工業工程，2016，19（1）：108-114.

[3] 李明，李前進. 項目多技能人力資源指派與調度混合算法[J]. 數學的實踐與認識，2017，47（19）：20-28.

[4] 康麗，馬塔·安德瑞. 基于時間窗的家庭醫療護理人力資源分配[J]. 工業工程與管理，2017，22（3）：83-92.

[5] 王一帆，劉士新，陳迪. 求解多技能人力資源約束的項目調度問題的兩階段算法[J]. 東北大學學報（ 自然科學版），2014，35（2）：184-189.

[6] 段鵬飛，余杰，聶慧，等．求解廣義優先關系下多技能人員項目調度問題的改進布谷鳥搜索算法[J]. 計算機應用研究，2018，35（5）：1315-1319．

[7] 李松，姜楠. 人力資源調度的蟻群算法模型[J]. 遼寧工程技術大學學報（自然科學版），2014，33（5）：679-682.

[8] 沈國軍. 基于改進遺傳算法的人力資源指派模型及方法[J]. 統計與決策，2014（16）：52-55.

[9] 伊雅麗. 研發型企業多項目人力資源調度研究——基于蟻群優化的超啟發式算法[J]. 工業工程，2018，21（4）：104-109.

[10] 吳建林. 含時間窗和多技能約束的人力資源路徑問題模型與算法研究[D]. 武漢：華中師范大學，2018.

[11] YANG X S， DEB S.Cuckoo search via Levy flights [C]／／proceedings of World Congress on nature amp; Biologically In?spired Computing，India：IEEE Publications，2009：210-214.

[12] 魏小迪，鄭洪清. 求解帶時間窗車輛路徑問題的改進離散花朵授粉算法[J]. 數學的實踐與認識， 2020， 50（2）：193-200．

[13] 劉敏. 改進的花朵授粉算法在物流配送中心選址問題中的應用[J]. 計算機應用與軟件，2019，36（6）：277-281，361．

［責任編輯 蘇琴］