參數化建模在多類型干擾效能預測中的應用

梁 懿 余建宇,2 王 超 文凱歌

(1.西安電子工程研究所 西安 710100;2.西北工業大學 西安 710072)

0 引言

針對脈沖多普勒雷達的干擾效能預測目前鮮有研究,但其基本思想和原理方法可以借鑒干擾效能評估。由于效能評估的主觀性較強,目前沒有公認準則。

崔炳福[1]系統介紹了干擾有效性評估理論;周林[2]等采用多屬性決策法提出了幾種有效性評估指標;袁凱[3]等基于雷達特點采用模糊算法判斷干擾效果;王博陽[4]提出了一種針對不確定性目標和評估時效性的在線雷達干擾評估方法;李志軍[5]等采用G1法與改進TOPSIS法評估干擾效果。以上方法均具有一定效果,但最大問題是計算復雜且主觀性較強。綜合以上方案選取的指標,本文決定從雷達干擾方程著手計算最小干擾距離[6-7],但其干信比參數設置往往依賴于研究和試驗人員的經驗積累,主觀性強,對最終預測結果影響較大。

本文基于趙國慶[8]著作的基本原理,研究自衛干擾機的遮蓋式干擾樣式[9],參照石曉娟[10]和張小飛[11]等人從能量和功率比較的角度,使用參數化建模的方法結合脈沖積累增益和時寬帶寬積,提出補償干信比計算方法,用于計算更為合理的干信比值,并結合Swerling起伏模型檢測概率[12]應用在多個干擾類型下針對脈沖壓縮雷達的干擾效能預測中。

1 補償干信比

實際雷達對抗中,干擾機與雷達平臺屬于非合作關系,無法直接獲取雷達平臺眾多指標信息[13]。通過對一些易于獲取的參數計算,得到干擾信號功率在雷達端信號和信息處理后相對于雷達回波信號的衰減,即為補償干信比,將該值作為干擾方程中的干信比參數,更具有參考意義。

1.1 指標確定

在合理性、系統性和科學性的原則指導下征詢雷達對抗領域專家意見后,運用參數化建模的思想建立了如圖1所示的補償干信比估算模型。

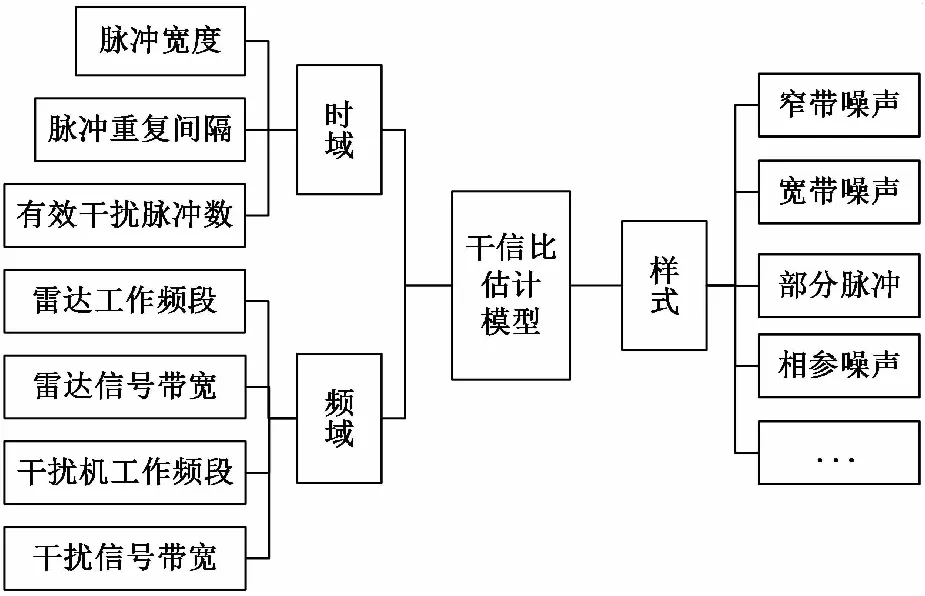
圖1 補償干信比的依據指標

1.2 補償系數的計算

1.2.1 平均干擾脈沖積累

雷達發射的脈沖信號經過目標散射及來回路程大氣衰減,最終雷達接收回波信號很小。其最有效的增益方式來自脈沖積累。對于轉發式干擾,干擾信號如要獲得脈沖積累增益,須接收擁雷達信號獲取其相參特性并采取干擾措施轉發該信號對雷達實施干擾。將干擾細化到雷達信號每個相參處理周期(Coherent Processing Interval,CPI)內能夠干擾的脈沖數,則定義平均干擾脈沖積累EPJ為

(1)

圖2 平均干擾脈沖積累示意圖

1.2.2 有效帶寬

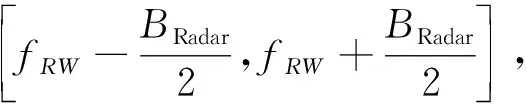
干擾機實際工作頻段為[fJ1,fJ2]。定義有效帶寬BFact為干擾機與雷達信號頻段重疊部分(見圖3)。

BFact=min(fR2,fJ2)-max(fR1,fJ1)

(2)

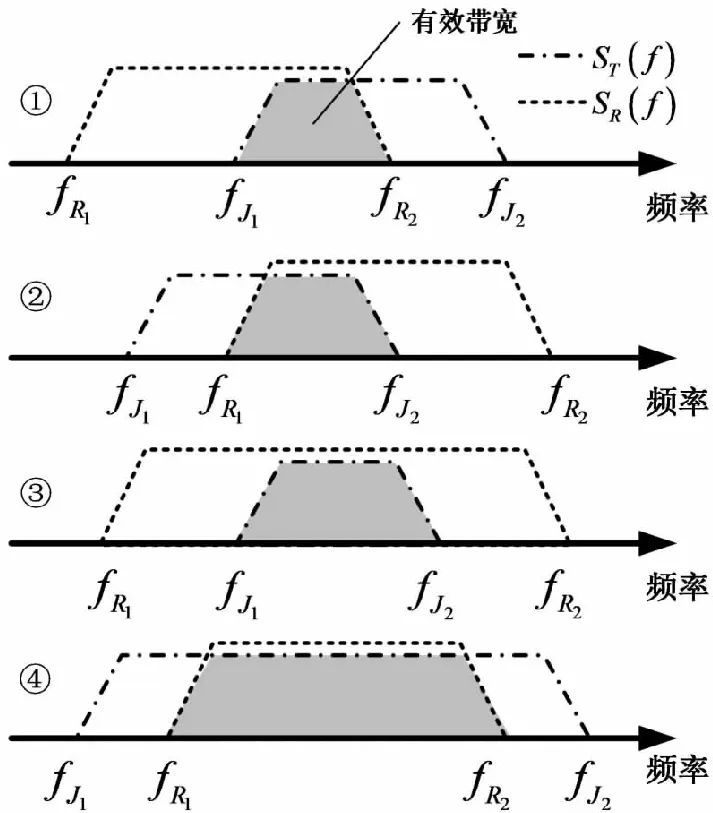
圖3 有效帶寬的幾種情況

1.2.3 干擾發射效率

如圖3所示,真正能夠用于干擾雷達積累脈沖的功率處于有效帶寬BFact上,故實際干擾發射效率為

(3)

從功率譜角度計算干擾發射效率與雷達接收效率較為復雜不便于干擾機實時計算,可以采用簡化帶寬比實現:在實際干擾情況中,干擾機工作的中心頻點一般會與雷達信號頻點對準,兩者功率譜大部分重疊。用有效帶寬與信號帶寬的比值大致可以表示發射效率。則有

(4)

其中ηT是干擾發射效率。

按上述方法計算效率,需要注意的是當一方頻段完全覆蓋另一方時,會出現ηT等于1。現實中由工程實現的限制,效率不可能達到1。本文會依據工程的先驗經驗設定一個系數對其加權。

1.2.4 有效脈寬比和有效功率比

圖4是對雷達脈沖進行部分脈沖干擾的時序原理圖。這其中涉及到兩個參數,一個是對雷達脈沖進行采樣的時間,另一個是對雷達脈沖發射干擾的時間。

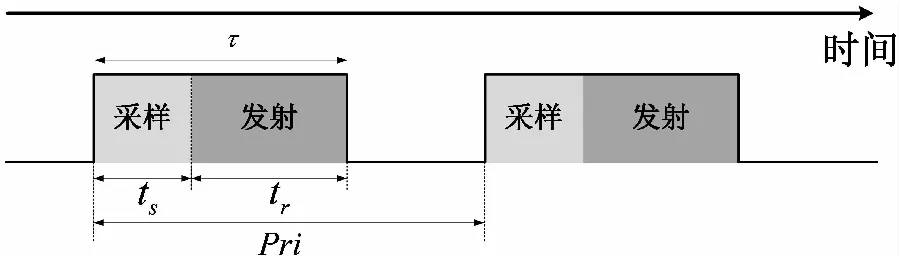
圖4 部分脈沖樣式時序原理

有效脈寬比:指一個雷達脈沖期間干擾機對其進行采樣和干擾時間占比的綜合度量:對雷達脈沖進行采樣時間占總脈寬越大,干擾機能夠獲取的雷達脈沖信息(如頻率、相位)等越多;發射干擾時間占總脈寬越大,干擾信號對雷達原信號在脈寬上覆蓋程度越高。定義有效脈寬比為

(5)

其中τ是雷達信號脈寬,ts是干擾機采樣時長,tr是干擾發射時長。

有效功率:指干擾機發射的所有能量中真正對雷達起到干擾作用的部分。不同干擾樣式可能會產生不同的功率浪費或損耗(例如某些干擾樣式會同時發射多個頻段的干擾信號,總能量會被各個頻段均分,非雷達信號瞬時頻段的干擾信號則無法對雷達干擾起作用)。根據描述,定義有效功率為式(6)所示。

(6)

其中Ptj是干擾機發射功率,Pte是能夠作用于實際干擾的信號功率。

1.3 補償干信比計算

前一小節敘述了各個補償系數的設置原理和計算方法,所有系數如式(7)所示。

C0={ηT,EPJ,ητ,ηPt}

(7)

得到所有系數組成的集合C0后,將各元素轉化為dB形式后累加可估算雷達信號處理后干擾信號相較于雷達回波會產生的損失為

Kj=∑(C0)dB

(8)

其中Kj是補償干信比,∑(C0)dB表示將集合C0中所有元素累加。

2 多種類型下的干擾預測

2.1 雷達作用距離計算

本文對最小干擾距離計算是從干信比著手,對雷達的仿真是整個系統信號功率級,不考慮太過細致的信號處理流程。根據該原則本文將基本雷達方程[14]引入與作用距離相關的大氣衰減率,使得該方程成為超越方程(9)為

(9)

方程參數說明詳見表1所示。

表1 雷達方程參數說明

由式(9)可知,目標到雷達距離增大時,傳輸損耗增大,相應地雷達最大探測距離隨之減小。此類方程可用如圖5的圖解法計算,分別以方程左式和右式為函數繪制曲線,兩條函數相交的點是該方程的解,即雷達最大作用距離。

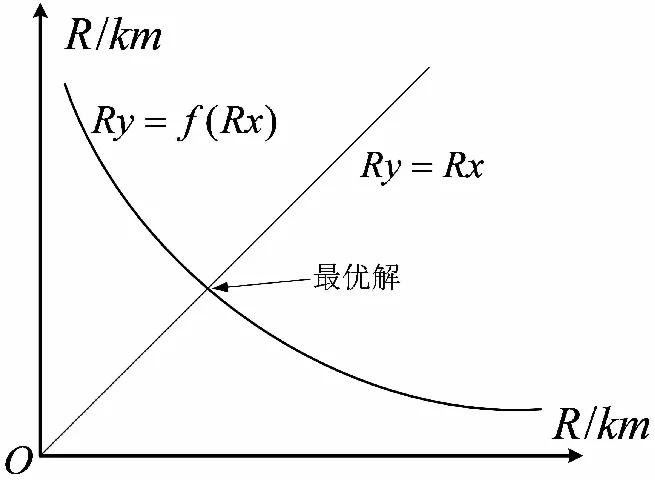
圖5 圖解法求解超越方程

2.2 基本干擾方程

根據雷達干擾概念定義:在遮蓋干擾情況下,雷達能夠發現目標的最大距離稱為燒穿距離[15];換個角度,干擾機恰好能夠對雷達進行正常干擾使其無法發現目標的距離,即為最小干擾距離。目標與雷達距離比該距離小,干擾信號功率不足以正常干擾雷達;反之,干擾信號功率足夠干擾雷達。

雷達接收到目標回波功率大小為

(10)

其中Rt是目標與雷達距離,其余參數的說明與表1一致。

由于干擾信號從干擾機處發射后,經過單程大氣損耗即可到達雷達處,故雷達接收到的干擾信號大小為

(11)

其中為Pj干擾機發射功率;Gj為干擾機天線增益;Gts為雷達接收干擾信號的天線增益;Ij為干擾信號脈沖積累個數;Rj為干擾機距雷達距離;Lj為干擾機系統損耗。

由式(10)、式(11)及干信比的定義,得到期望干信比為

(12)

(13)

由定義知期望干信比Ke與補償干信比Kj互為倒數,故根據式(13)可以得到基本干擾方程為

(14)

干擾方程也是一個超越方程,可用圖5的圖解法得到最優解。

2.3 多類型下最小干擾距離計算

由于干擾類型不同,干擾機與掩護目標位置關系、掩護目標編組數量變動等因素會導致基本干擾方程中參數有所變動,下面將按照自衛干擾、隨隊支援、遠距離支援、近距離支援四種類型(見圖6所示),分別討論最小干擾距離的計算。

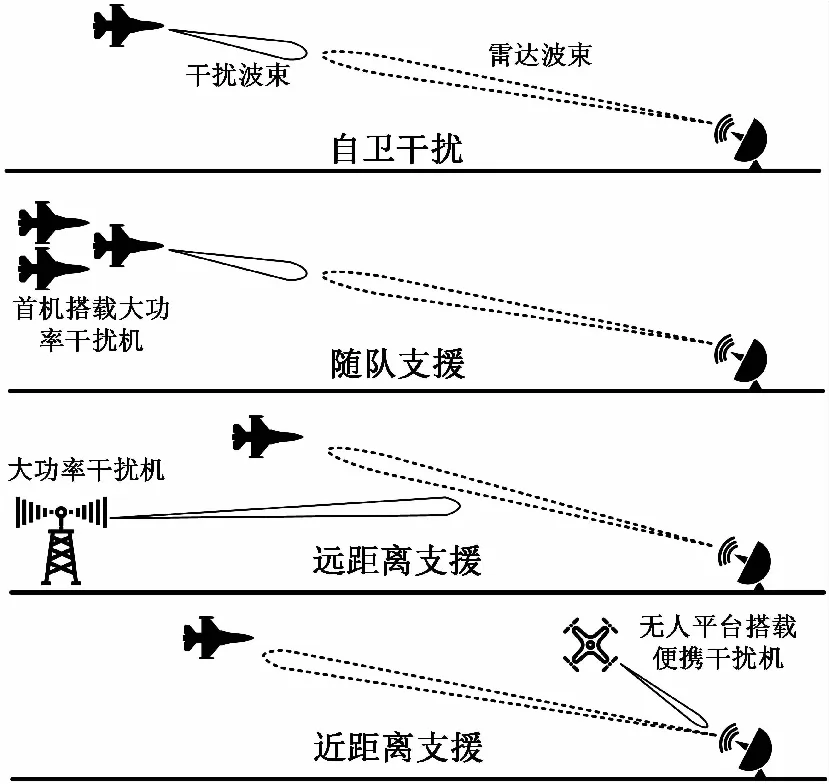
圖6 干擾類型示意圖

2.3.1 自衛干擾

自衛干擾(Self-screening Jamming,SSJ)是最常見的干擾類型[16]。電子干擾設備安裝在欲保護的平臺上(如飛機、軍艦、地面基地),干擾信號從雷達天線主瓣進入接收機,目的是擺脫敵雷達跟蹤和后續攻擊。根據設計情況可以使用遮蓋干擾和欺騙干擾。SSJ是現代作戰飛機、艦艇、地面重要目標等必備的干擾手段[17]。

由于電子干擾設備安裝在掩護目標平臺本身上,兩者到雷達距離相等(Rj=Rt),故自衛干擾類型下的最小干擾距離為式(15)所示。

(15)

2.3.2 隨隊支援

隨隊支援干擾(Escort-support Jamming,ESJ)類型中,干擾機位于目標附近,通過輻射強干擾信號掩護目標。它的干擾信號是從雷達天線的主瓣(ESJ與目標不能分辨時)或旁瓣(ESJ與目標可分辨時)進入接收機的,一般采用遮蓋性干擾。掩護運動目標的ESJ具有同目標一樣的機動能力。空襲作戰中的ESJ往往略微領前于其它飛機,在一定的作戰距離上還同時實施無源干擾。出于自身安全的考慮,進入危險區域時的ESJ常由無人駕駛飛行器擔任。

假設一個分組內共n架飛機,由前出飛機負責整個分組的電子掩護,若干擾信號由主瓣進入雷達接收機,最小干擾距離為

(16)

若干擾信號由旁瓣進入雷達接收機,最小干擾距離為

(17)

其中Gsl是雷達天線旁瓣增益,n是分組飛機總數。

2.3.3 遠距離支援

遠距離干擾(Stand-off Jamming,SOJ)類型中,電子干擾設備通常安裝在一個遠離防區的平臺上(即遠離敵方武器的威力范圍)。SOJ的目的通常是擾亂敵防空戰線的搜索雷達,以使已方的攻擊部隊能安全地突防進入敵領地。

由于電子干擾設備遠離掩護目標,處于雷達天線的非主瓣區域,最小干擾距離為

(18)

2.3.4 近距離支援

近距離支援(Stand Forward Jamming,SFJ)類型中,干擾機到雷達的距離領先于掩護目標,通過輻射干擾信號掩護后續目標。由于距離領先,干擾機可獲得寶貴的預先引導時間,使干擾信號頻率對準雷達頻率。主要采用遮蓋性干擾。距離越近,進入雷達接收機的干擾能量也越強。由于自身安全難以保障,SFJ主要由投擲式干擾機和無人機擔任,無人機蜂群作戰應用于SFJ也是近年來一大熱門研究點。

由于干擾機距離雷達較近,干擾信號從雷達主瓣與副瓣進入均有可能。若干擾信號從雷達主瓣進入,則干擾方程為

(19)

若干擾信號從雷達副瓣進入,則干擾方程與式(18)一致。

2.4 干擾效能判定

2.4.1 干擾概率

根據上文推導的最小干擾距離方程得出最優解Ropt和目標雷達距離Rt相比較:

1)若Ropt≤Rt則目標在最小干擾距離外,干擾信號功率大于回波信號,能夠完全壓制,此時干擾概率為1。

2)若Ropt>Rt則目標在最小干擾距離內,干擾信號功率小于回波功率,不一定能夠完全壓制,此時干擾概率根據Swerling起伏目標模型在一定虛警概率Pfa下(假設目標起伏狀態滿足Swerling I-V型模型)的檢測概率PD計算得到

PJam=1-PD

(20)

Swerling I-V型起伏模型在不同脈沖積累下檢測概率曲線不同,考慮到干擾概率計算的相對平滑性及干擾信號也能獲得部分脈沖積累增益的特點,本文假設雷達誤報概率極低,選取Pfa=10-9情況下CPI=10的曲線(見圖7所示)用于計算最小干擾距離內的干擾概率。

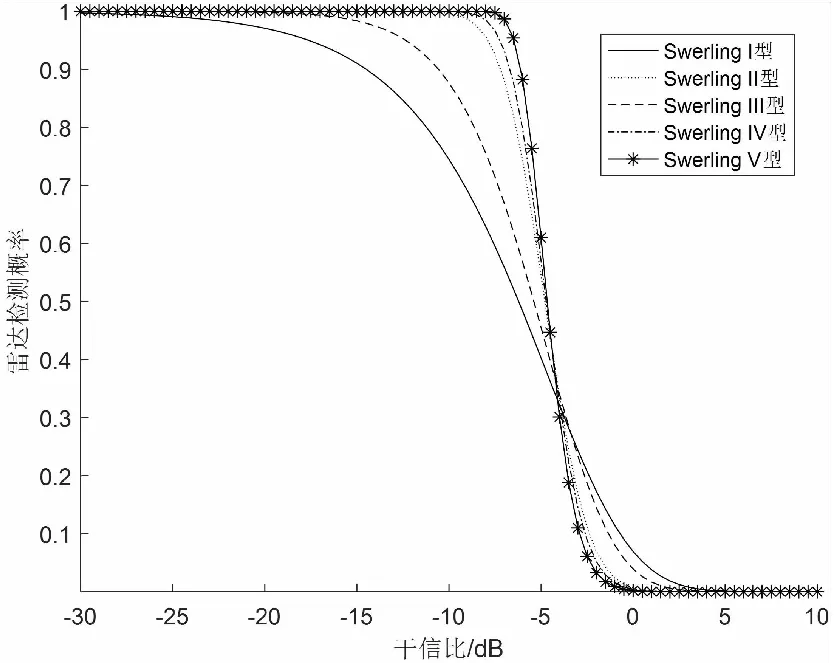
圖7 Pfa=10-9,CPI=10時不同起伏類型檢測概率

2.4.2 雷達威力削減

雷達最大探測距離RDmax可通過第二小節式(9)雷達作用距離方程求出,再結合各個類型下求出的最小干擾距離Ropt,可得到雷達威力削減計算式為

(21)

使用干擾概率和雷達威力削減兩個標準,再結合類型、雷達與干擾機性能參數等條件,可以得出較為直觀的干擾效能預測結果。

3 多種類型干擾效能預測仿真

相較傳統方法,本文采用的方法最大特點為:根據不同干擾類型和干擾信號樣式,得到一個比經驗參數(通常假設為10～20dB)更準確、先驗依賴性更弱的干信比,從而得出更貼合當前干擾狀態的最小干擾距離及參考干擾概率,能夠對干擾效能進行定量預測。本部分將以某型機載多功能雷達為例進行仿真試驗,從而說明這種方案在電子對抗論證和干擾測試時的參考價值。

3.1 雷達與干擾機參數設置

某型機載多功能雷達參數如表2所列。

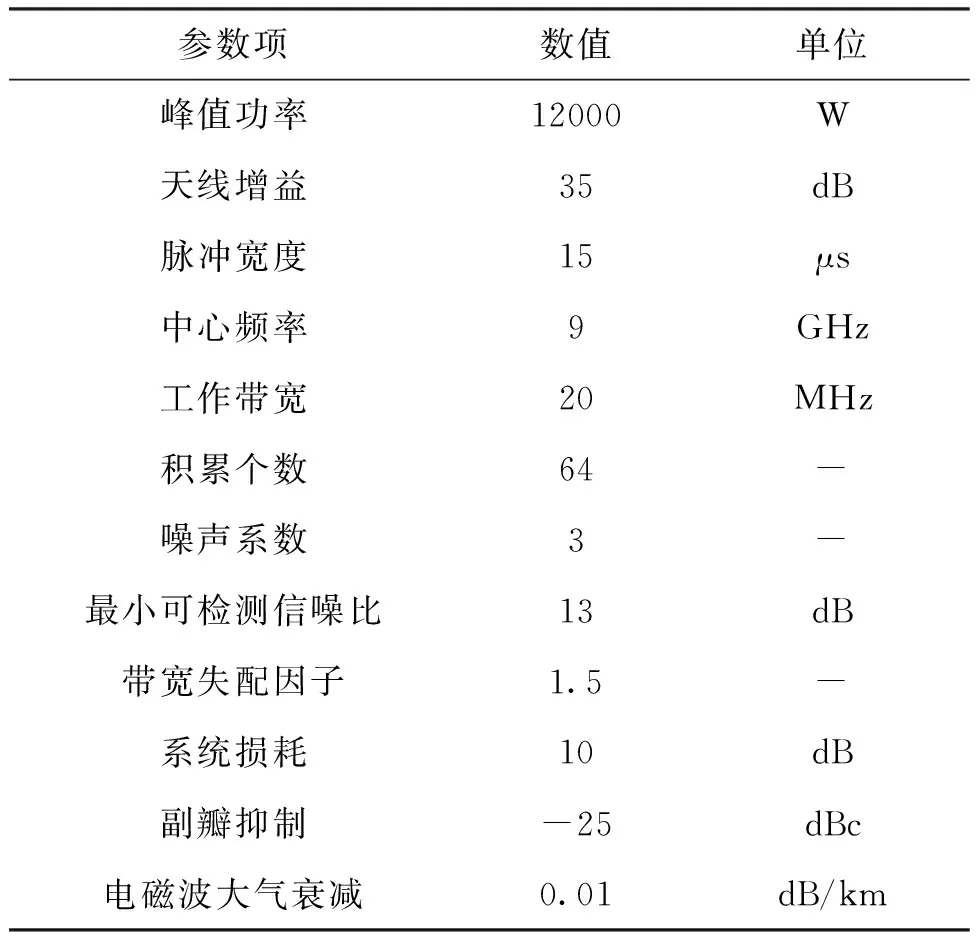
表2 某型機載多功能雷達參數

干擾機按使用類型不同分為小功率便攜式自衛干擾機與大功率壓制干擾機,具體參數如表3所示,數值欄“/”左側為小功率便攜式干擾機數據,右側為大功率壓制干擾機數據。

表3 干擾機參數

3.2 類型與干擾樣式設置

3.2.1 類型設置

1)自衛干擾:該類型中干擾機放置在掩護目標上,兩者與雷達距離相等,在設置類型參數時只需指定目標雷達截面積RCS、Swerling起伏類型和與雷達距離即可。

2)隨隊支援:與自衛干擾類似,干擾機放置在與掩護目標同一編組的某一平臺上,該平臺與掩護目標一同行動,可以視作兩者與雷達距離相等。該類型除了指定目標RCS、Swerling起伏類型、距雷達距離外,還需指定編隊中目標數量。

3)近距離支援和遠距離支援:這兩種類型中干擾機與掩護目標不在同一距離,除了與自衛干擾相同設置外,還需依具體類型指定干擾機距離。

3.2.2 干擾樣式設置

采用寬帶噪聲、窄帶噪聲、相參噪聲和部分脈沖四種干擾樣式對雷達進行干擾,干擾參數設置如表4所示。

壓制式干擾(寬帶噪聲、窄帶噪聲)采取的策略是使用大功率噪聲對雷達全頻段覆蓋以期抬高雷達檢測門限。

轉發式干擾(相參噪聲、部分脈沖)從補償干信比的計算原理看,單次采樣、發射時間越長最終功率越大,但實際情況中對雷達有效干擾需要使得雷達在MTD處理后距離維出現盡可能多的干擾尖峰,以此抬高CFAR檢測門限。對于采樣、轉發時間較短導致功率不足問題,轉發式干擾信號可通過獲得部分相參積累增益來改善。因此轉發式干擾常采用較小發射間隔發射脈沖干擾來達到功率與距離維干擾數的平衡。

表4 干擾樣式設置

3.3 仿真演示

按照前文所述的各參數設置,通過Matlab仿真來計算多種干擾類型下的雷達作用距離、最小干擾距離、實際干信比、參考干擾概率及雷達威力削減。

3.3.1 自衛干擾及參考干擾概率驗證

首先討論同種干擾類型下不同干擾樣式對干擾效能的影響:類型為自衛干擾,目標RCS=20m2,起伏類型為Swerling III型,選取便攜式小功率干擾機搭載在掩護目標上,距雷達50km依次使用寬帶噪聲、窄帶噪聲、相參噪聲、部分脈沖四種方式進行干擾,分別如圖8(a)至圖8(d)所示。

圖8 自衛類型下多種干擾樣式對比

在其它條件相同的情況下,轉發式干擾由于擁有相參特性可以獲得脈沖積累增益,頻域對準能量利用率高,最終干擾效果優于壓制式干擾。壓制式干擾信號能量分散在較寬的帶寬上,利用率低且沒有相參特性,最終干信比較低。尤其是寬帶噪聲干擾結果中,掩護目標處于最小干擾距離之內,無法受到有效保護。

窄帶噪聲干擾的最小干擾距離為29.27km,目標在50km時,干擾機能夠完全掩護目標。目標與雷達距離逐漸縮小,取33km、27km和12km驗證參考干擾距離的變化,如圖9、圖10和圖11所示。

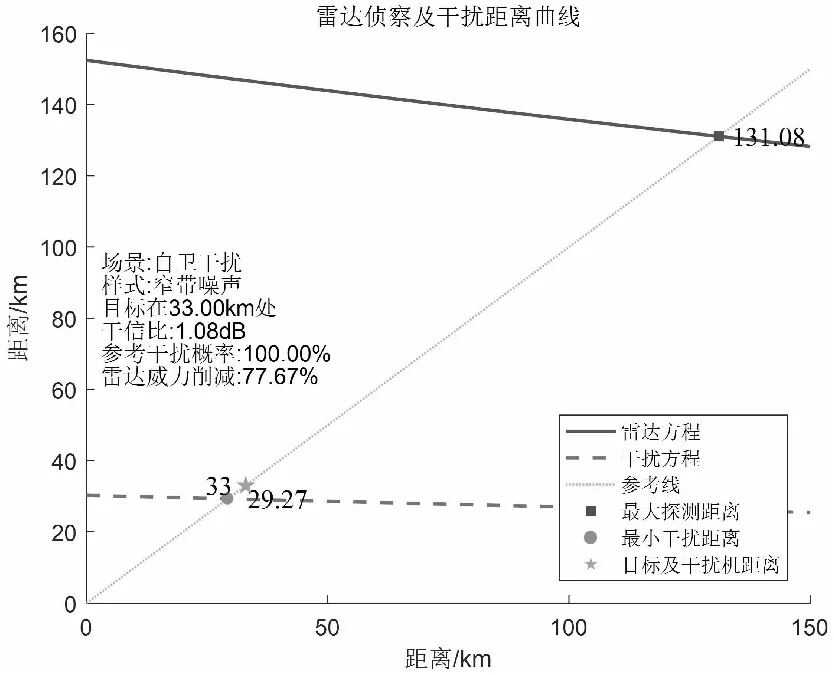
圖9 目標在33km處參考干擾概率

圖10 目標在27km處參考干擾概率

圖11 目標在12km處參考干擾概率

目標處于33km時,雖然在最小干擾距離之外,但其干信比只有1.08dB,干擾信號對雷達回波功率的壓制效果已經不明顯。目標處于27km時,干信比小于0,此時已無法保證100%干擾效率,而是根據Swerling起伏模型計算對應干信比下的干擾概率,當目標處于12km時,干信比為-7.92dB,參考干擾概率為25.10%,幾乎無法對雷達產生有效干擾。故最小干擾距離作為判斷干擾效能臨界點是一個較為合適的值。

3.3.2 隨隊支援

大功率干擾機能量轉換率低(通常低于20%),體積龐大不便用于自衛用途攜帶。一般放置在雷達探測距離外對挺進的掩護目標進行遠距離支援干擾或由一個平臺搭載后編入需掩護的編隊進行隨隊支援干擾。

假設隨隊干擾類型,包括搭載大功率干擾機平臺共3機編隊距雷達50km,每個目標RCS=20m2,起伏類型為Swerling Ⅲ型。采用相參噪聲對雷達主瓣干擾,結果如圖12所示。

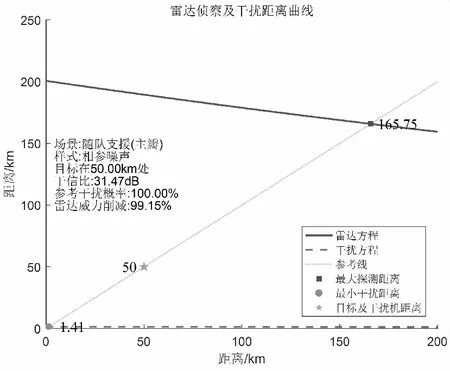
圖12 隨隊支援下相參噪聲主瓣干擾

得益于于大功率干擾機的發射功率和天線增益,隨隊支援下采用窄帶噪聲干擾和相參噪聲干擾都能取得較好的壓制效果。但編隊中須有一個作戰平臺用于搭載大功率干擾設備,毀傷武器的負載相應減少,編隊整體進攻能力會降低。

如果編隊內飛行器數目較大、隊形分散或RCS較大,當雷達照射編隊邊緣目標時,干擾信號會從副瓣進入雷達。如圖13所示,編隊飛機數量增加至9架,單機RCS不變,最小干擾距離增幅明顯,干信比也相對較低,干擾能力大打折扣,當掩護目標體型較大或數量較多時,對每個目標單獨使用自衛干擾是更明智的選擇。

圖13 隨隊支援下相參噪聲副瓣干擾

3.3.3 遠距離支援

若將大功率干擾機應用在遠距離支援中,假設目標距雷達45km,RCS=20m2,起伏類型為Swerling Ⅲ型,干擾機在距雷達140km處掩護目標。分別采用窄帶噪聲和相參噪聲對雷達干擾,仿真結果如圖14、圖15所示。

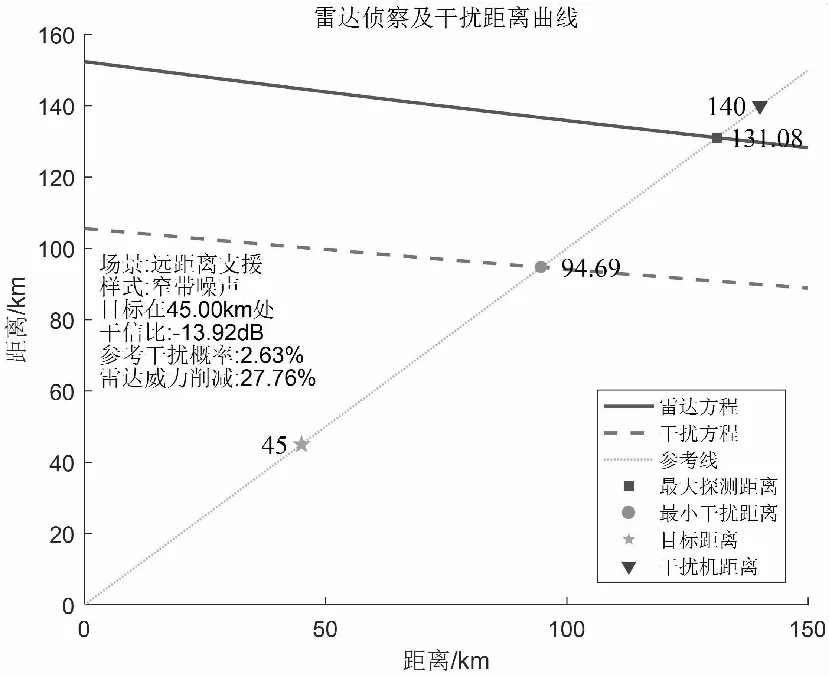
圖14 遠距離支援下窄帶噪聲干擾

圖15 遠距離支援下相參噪聲干擾

遠距離支援類型下,由于干擾波束不易對準雷達主瓣且干擾距離較遠,干擾信號損失大。壓制式干擾與遮蓋式干擾對雷達威力削減效果均不佳,45km處的干信比也不理想。采用更大功率干擾設備雖可以改善這種情況,但系統復雜度高不易實現。遠距離支援最大短板是距離戰場較遠,無法根據戰場實時戰況及時更換干擾策略。

3.3.4 近距離支援

小功率便攜式干擾機由無人平臺搭載后,可以先于掩護目標沿前進方向至更靠近雷達的距離對其進行干擾。在近距離支援類型下,假設目標距雷達45km,RCS=20m2,起伏類型為Swerling Ⅲ型。

搭載便攜式干擾機的無人設備RCS=0.01m2,根據雷達最大探測距離計算,該設備在22.22km處會被雷達探測。故設定該無人設備在25km處投放并開啟干擾,干擾樣式選擇部分脈沖。對雷達主瓣和副瓣干擾結果如圖16、圖17所示。

圖16 近距離支援下部分脈沖主瓣干擾

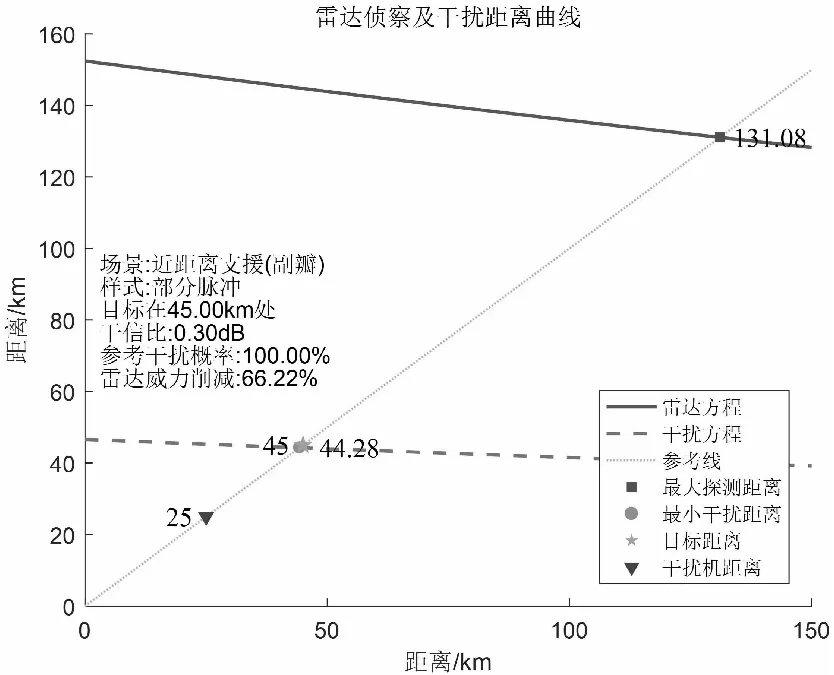
圖17 近距離支援下部分脈沖副瓣干擾

兩種情況下,雖然都能起到保護目標的作用,但干擾信號從雷達副瓣進入后干信比較差,干信比幾乎為0。想要得到更理想的干信比,需要無人平臺盡量靠前及盡可能從主瓣進行干擾,但這又對無人平臺飛行性能指標和隊形控制提出了很高的需求。

在干擾設備小型化、便攜化發展的大趨勢下,綜合炮射式干擾彈、小型長續航無人機集群作戰體系的發展及系統成本復雜度考量,今后的干擾策略多會圍繞自衛干擾與近距離支援采用靈活性更強的轉發式干擾,輔以隨隊支援和遠距離支援采用壓制式干擾來實現。

4 結束語

國內電子對抗領域廣泛采用干擾方程來計算遮蓋式干擾最小干擾距離,但決定該距離的干信比參數往往是一個經驗數值。針對該問題,本文通過參數化建模,基于補償干信比并結合不同類型干擾方程對干擾效能進行合理預測。建立的模型可直觀看出干擾效能定量預測,對電子對抗的總體論證和干擾樣式的研究具有一定參考意義。

由于篇幅限制,本文仍有許多可以完善的地方:比如在干擾類型設計中,為簡化模型將干擾方向只分為主瓣和副瓣,后續完善可采用雷達方向圖,從各個方向進行干擾均有不同接收增益;以及預測方法顆粒度較大,對雷達接收回波信號作簡化處理,沒有過多體現雷達系統的信號級處理過程。故將這一思想方法寫出,期望能夠起到拋磚引玉的作用,便于同行學者和研究人員交流學習。