基于SEA的常規導彈封鎖機場跑道作戰效能分析的系統建模和解析
李新其,李紅霞,邱艷粉
(1.火箭軍工程大學 初級指揮系,陜西 西安 710025;2.西北政法大學 軍民融合發展研究院,陜西 西安 710025;3.中國人民解放軍96723部隊,廣西 柳州 545000)
常規導彈武器系統效能分析的方法大致分為統計試驗方法和解析方法兩大類[1]。解析法具有公式透明性好、推導過程嚴密、理論體系完備等優點,便于快速分析武器系統的作戰效能;系統效能分析(system effectiveness analysis,SEA)方法是目前效能分析理論中研究復雜動態環境下系統效能的最得力工具,具有較強的分析能力與廣泛適用性[2-3]。
目前,以跑道失效率(disability pavement rate,DPR)為指標的封鎖把握程度的建模研究都以成爆彈量(成功命中單個目標所需導彈數量)為基礎和前提,但無法描述動態、不確定條件下突防戰法、突防技術對于作戰效果的影響[4-6]。因此,在推導出封鎖把握程度的解析模型后,還必須根據導彈攻防體系對抗的特點,對封鎖把握程度的分布密度進行統計推斷分析[7]。因此,本文從作戰效能分析理論的基本原理出發,結合常規導彈封鎖機場跑道的作戰特點,建立一種常規導彈封鎖機場跑道作戰效能分析的解析方法。在此基礎上,根據SEA效能分析的要求,結合現有研究成果,建立了封鎖時間性能量度的解析計算模型,并重點就封鎖時間性能量度的分布函數進行統計推斷。
1 基本框架
運用SEA方法分析常規導彈打擊機場跑道作戰效能的步驟如下:
①確定常規導彈封鎖作戰的系統、環境和使命。
這里,系統指常規導彈武器系統。環境指與系統發生作用而不屬于系統的所有元素的集合。如圖1所示,展示了導彈武器系統與作戰環境。
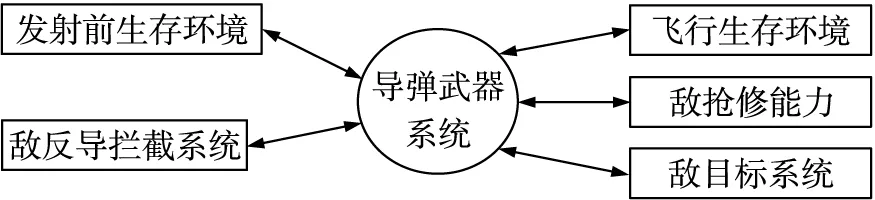
圖1 導彈武器系統及其環境Fig.1 Missile weapon system and its environment
可用以下兩方面數據作為描述系統環境的環境原始參數:一是目標信息,包括跑道長Lx、寬Ly,最小起降窗口長Lx,min、寬Ly,min,單彈坑平均修復時間等;二是導彈飛行環境參數,包括各類反導防御武器系統的組成、部署、技術戰術指標、戰法等。令A表示所有環境原始參數組成的向量。
使命是系統運動過程的秩序,常規導彈武器系統封鎖機場的使命就是使敵空軍基地在一定時間內喪失保障飛機起降的主要功能。
②由作戰使命抽象出性能量度空間{Oi}。
描述系統完成使命品質的“量”稱為性能量度或屬性,記為O。第i個性能量度則記為Oi,i=1,2,…,n。令描述封鎖把握程度的性能量度及跑道封鎖時間分別用O1和O2表示,則:
式中:φDPR為跑道失效率,tf為跑道失效時間。
③根據封鎖作戰特點,建立系統原始參數到性能量度的映射。
描述系統能力,影響性能量度的獨立變量被稱為系統原始參數,這里主要指武器方面的性能及數據,如武器精度、拋撒半徑、裝填子彈數、單枚子彈對跑道的毀傷能力(毀傷面積),發射彈量、發射成功率、飛行可靠性、突防概率等。令V表示所有系統原始參數組成的向量。如果性能量度空間O是n維的,那么
{Oi}v={fvi(V,A)}v,i=1,2,…,n
根據攻防對抗環境和封鎖與反封鎖對抗過程,需要分別建立O1和O2的映射,即研究突防及封鎖與反封鎖對抗條件下跑道失效率φDPR和跑道失效時間tf的建模問題。
④根據封鎖作戰的任務要求,建立使命原始參數到性能量度的映射。
用于描述使命特征的基本變量稱為使命原始參數,這里使命原始參數就是作戰要求的封鎖時限和封鎖把握程度。令G表示所有使命原始參數組成的向量。使命映射通過把使命原始參數的值域要求轉化為性能量度O的值域要求而實現。顯然使命映射fg(G,A)也應是n維,且有:
{Oi}g={fgi(G,A)}g
導彈部隊封鎖機場跑道的任務要求可以簡單表示為至少封鎖機場若干時間(tXX)的把握程度不低于某一概率(PYY),其使命軌跡在性能空間內的區域必須滿足不等式:
⑤由fv和fg在{Oi}空間上產生系統軌跡Lv和使命軌跡Lg。
假設經過推導或統計分析得到O1和O2的分布密度函數,分別記為f1(O1)和f2(O2);O1和O2的聯合分布密度函數記為f(O1,O2)。根據前文的分析,可以畫出系統映射和使命映射在性能空間{Oi}上所生成的系統軌跡Lv和使命軌跡Lg。如果O1和O2的分布密度函數相互獨立,當f1(O1)和f2(O2)都為正態分布,或都為均勻分布時,Lv和Lg的關系分別如圖2、圖3所示。
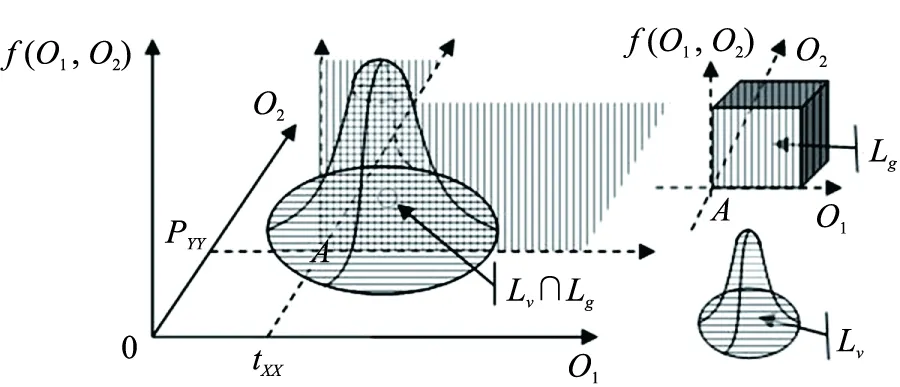
圖2 正態分布下性能量度空間上示意圖Fig.2 Performance measure space under normal distribution
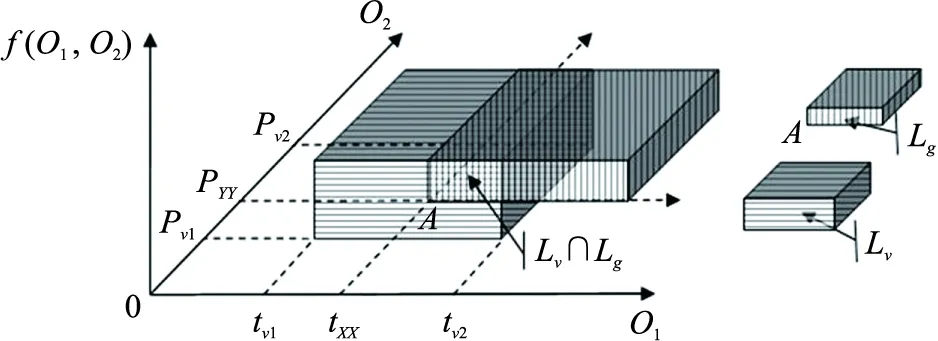
圖3 均勻分布下性能量度空間上示意圖Fig.3 Performance measure space under uniform distribution
⑥根據兩軌跡空間的重合程度求解封鎖作戰效能E。
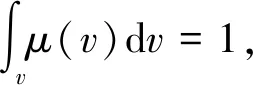
(1)
式中:Lv∩Lg為系統軌跡Lv與使命軌跡Lg的交集。
根據式(1),可以計算出常規導彈封鎖機場跑道的作戰效能E。如果f1(O1)和f2(O2)相互獨立,聯合分布密度函數f(O1,O2)=f1f2,則常規導彈封鎖機場跑道的作戰效能為
E=?Lv∩Lgf1(O1)f2(O2)dO1dO2
2 封鎖把握程度的解析模型
2.1 成爆彈威力環“切割”跑道的解析模型
為解決子母彈封鎖機場跑道毀傷效果指標計算的解析算法問題,本文提出采用威力環“切割”跑道思想8-9]。具體思想為:
①按最小起降窗口的長度要求,將跑道“切割”分成若干段;
②假設子彈在拋撒圓內均勻散布,其半徑為Rth,子彈對跑道的平均毀傷半徑為Rde,用Rλ表示威力環半徑,則Rλ=Rth+Rde。
③當導彈拋撒子彈后形成的威力環使跑道不存在供飛機起降的最小起降窗口時,認為該段跑道被成功“切割”。
④綜合各段跑道成功“切割”的概率,得到多枚彈打擊下整條跑道的失效概率。
按以上思想可以得到單瞄準點、單枚成爆彈情況下,跑道被成功“切割”概率的解析表達式[10]。
命題一假設第j段待“切割”的跑道,其寬為Ly,b,其長為2Lx,d,最小起降窗口長Lx,min,寬Ly,min,導彈的瞄準點位于該段跑道中央。第j段跑道被一枚成爆彈成功“切割”的概率[5]的解析計算式為
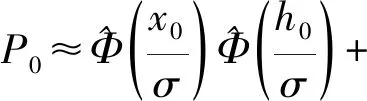
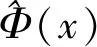
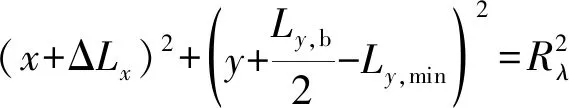
證明
1)以跑道中心為原點,跑道方向為x軸方向,建立直角坐標系。
根據瞄準點選取方法,可知待切割的長為2Ld這段跑道,一般2Lx,d≤2Lx,min,令ΔL=Lx,min-Lx,d。
2)根據母彈落點、威力環與被“切割”跑道之間的幾何關系,確定有利彈著區。
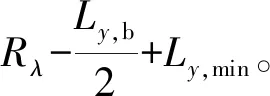
②母彈彈著點向左移動。顯然橫向(即左右方向)之間的移動,不能超過-Rλ-ΔLx。
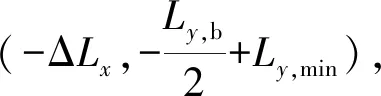
④母彈彈著點向其他方位移動。
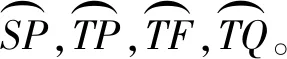
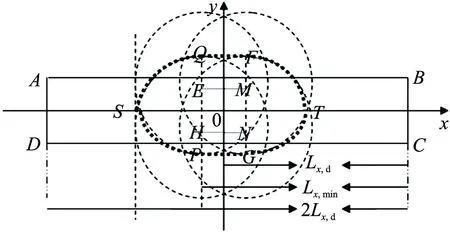
圖4 母彈有利彈著區示意圖Fig.4 Schematic diagram of the favorable impact area of projectile
3)計算單瞄準點、單枚成爆彈情況下,某段跑道被成功“切割”的概率。
根據火力運用理論可知,求某段跑道被成功“切割”的概率,就是計算母彈落入有利彈著區內的概率。為此,做如下假設:
①導彈瞄準點與落點中心重合,即不考慮系統誤差;
②母彈彈著點散布為圓散布,即σx=σy=σ,彈著點縱向和橫向的分布密度分別為
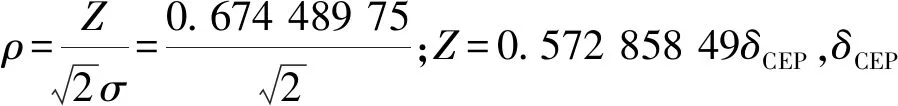
為便于計算,把圖4中的有利彈著區劃分為5個部分,如圖5所示。
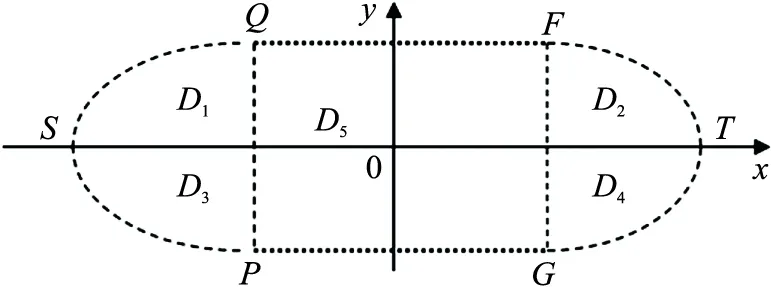
圖5 有利彈著區劃分示意圖Fig.5 Carve out spheres of favorable target
彈著點于有利彈著區內的概率為
由于正態分布密度函數對于分布中心(與瞄準點重合)是點對稱的,而區域SQFTGP對于瞄準點也是點對稱的,且被積函數相等,所以:P{(x,y)∈D1}=P{(x,y)∈D2}=P{(x,y)∈D3}=P{(x,y)∈D4}。
對于D1有:
為保證計算積分的精度,將區域按x0,x1,…,xn等距離分割,則:
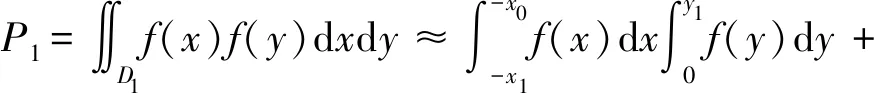
同樣,可得到P2,P3,P4的積分表達式。經整理得:
對于D5,知其為一矩形區域,即:
簡化為
故單瞄準點、單枚成爆彈情況下,某段跑道被成功“切割”的概率P0為
證畢。
2.2 跑道失效率的解析計算模型
在此基礎上,可以推導出多枚成爆彈、多瞄準點情況下跑道失效概率的計算式。
推論設某跑道瞄準點有m個,與各個瞄準點相對應的各枚導彈發射、突防及解爆情況如表1。表中,解爆成功率為導彈命中機場跑道后,在爆炸前的一定時間內,被對方解除爆破的成功概率。

表1 瞄準點與各枚導彈的發射成功概率、突防概率及解爆成功率關系表Table 1 Aim point and probability of Successful launch,Penetration probability,probability of Successful disexplosion
則跑道失效率的計算式為
(2)
式中:P0,ε為第ε枚成爆彈成功“切割”某段跑道的概率。
2.3 封鎖把握程度O1分布規律推斷
突防情況對封鎖把握程度計算結果的影響是顯著的,需結合具體的作戰環境,對O1的計算結果進行分析推斷。
在設定具體攻防對抗條件的基礎上,主要考慮運用古典概率論方法研究各突防事件出現的概率,根據各突防事件的成爆彈量情況計算相應的φDPR值,再綜合得出φDPR值的概率分布情況,最后對數據進行回歸分析,推斷φDPR服從何種分布。
2.3.1 問題描述
在導彈攻防對抗環境描述中,多枚導彈成功突防的概率服從二項式分布:
式中:Nmax為反導系統可同時攔截的來襲導彈枚數的最大值;N0為Nmax枚導彈中突防成功的枚數;Pxy為反導武器對來襲導彈的攔截概率,1-Pxy為突防概率。
假設常規導彈部隊為打擊某機場跑道,瞄準點的選擇和分配彈量分別為θ和αθ,其中θ=1,2,…,m。

表2 發射導彈編號與瞄準點對應關系表Table 2 Missile number and its aim point
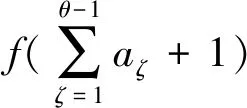
2.3.2 確定基本事件
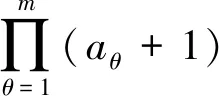
2.3.3φDPR的分布函數
令某枚導彈被攔截記為“0”,該枚導彈成功突防記為“1”,某次突防對抗的結果可表示成如表3所示。

表3 發射導彈編號與瞄準點對應關系表Table 3 The missile number and its aim point
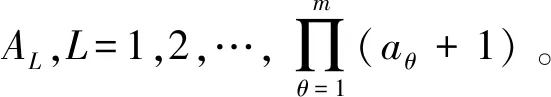
P{φDPR=φDPR(AL)}=P(AL)
根據上式,得到φDPR的分布函數:
F1(φDPR)=P{φDPR≤φDPR(AL)}
2.3.4φDPR分布密度統計推斷
大量的統計分析表明,對于導彈的發射成功率、飛行成功率等成敗型事件,其參數大都服從于Beta分布[12],在推斷φDPR的概率密度函數時,首先假設其近似服從Beta分布。
Beta分布的密度函數為
式中:0 2.3.5 關于模型計算精度的說明 用解析法建立起來的跑道失效率計算模型存在系統誤差。按本模型計算出來的結果,要略低于實際值,故要分析其計算的精度。 命題二本模型的計算精度估算公式為 根據該精度估算公式,可以計算出母彈拋撒半徑Rth=200 m,子彈毀傷半徑Rde=200 m,δCEP=180 m,最小起降長度為800 m,實際選取瞄準點間隔為700 m時的φDPR計算精度,其值為0.951 9;即使當實際選取瞄準點間隔為750 m時,模型的計算精度仍有0.913 8,此計算精度可以滿足作戰需要。 3.1.1 排爆作業過程的描述 為構建延時子母彈排爆時間的計算模型,做出如下假設: ①攻方在對機場跑道進行打擊時,可單獨使用侵徹子母彈,也可組合使用延時子母彈,侵徹子母彈中的子彈成爆率為Px,未爆子彈和延時子母彈都視為排爆對象; ②所投放的所有子彈在跑道上分布均勻,且彈坑不重合; ③為保證跑道在最短時間內恢復一定的起降能力,排爆分隊僅對某塊能夠滿足飛機最小起降要求的矩形區域進行排爆作業; ④起爆時間按正態分布模型裝定,即:在侵徹跑道35~65 min的時間范圍,以均值為50 min,標準差為5 min進行裝定; ⑤機場排爆分隊有M1組人機系統,每組均可獨立作業(或并行作業),每組系統可經受k次毀傷; ⑥延時子母彈的反排概率為Pr,每個排爆小組排除一枚延時子母彈的平均時間為t,并定義一輪排爆任務,是指各排爆小組同時開始排爆,每組都排完一枚未爆彈或延時子母彈所需的時間,可以認為每輪的時間均相同,都為t; ⑦當全部排爆小組都被炸毀,排爆作業視為癱瘓,停止排爆,彈坑搶修分隊直接開始作業[13-14]。 3.1.2 排爆時間建模 根據前文中命中跑道子彈數的計算方法,可以得到某塊最小起降窗口區域內實際含有的未爆侵徹子母彈和延時子母彈的總數,記為M2每個排爆小組一次只對一顆子彈進行排爆,則M1個排爆小組完成第一輪排彈任務時,共對M1枚子彈進行排爆操作,其中反排成功的彈為M1(1-Pr)個,則有M1Pr個排爆小組受到一次損傷。記每組受損傷概率為Pda,則Pda=Pr。由于每個排爆小組可承受k次損傷,定義每個小組的受損傷狀態集為D={W0,W1,…,Wk}。對于任意一個排爆小組在排除n枚彈時,所處的狀態是一個隨機變量,記為Xn。由于對任意n≥1,該小組的狀態值都只與前一輪狀態值有關,故這是一個馬爾科夫鏈[15]。 M1個排爆小組處于狀態Wρ的有: 當所有的排爆小組都處于Wk狀態時,有: M1個小組參與第n輪時所排除的彈數為 完成第n輪排爆作業時所排除的彈數為 完成第n輪排爆作業所用時間為tc=nt。比較M2與M3,當M2=M3時,表示完成了最小起降區域的排爆工作。 3.2.1 彈坑搶修過程的描述 彈坑搶修過程指跑道搶修分隊在搶修區域內填補彈坑、修復道面的過程。對機場封鎖與反封鎖對抗過程的4個階段進行描述的基礎上給出如下假設: ①為保證跑道在最短時間內恢復一定的起降能力,跑道搶修分隊采取重點搶修策略,即彈坑搶修分隊的作業區域為某塊能夠滿足飛機最小起降要求的矩形區域; ②最小起降區域內需修復的彈坑總數應為已爆侵徹子彈(其成爆率為Px)與排爆失敗后延時子彈彈坑數(其反排概率為Pr)之和,令Mx1、Mx2分別為落入跑道的侵徹、延時子母彈總數,則彈坑總數M4為 ③跑道搶修分隊的編組能力視子母彈戰斗部的毀傷威力的不同而相應變化,對第ω型戰斗部,可編成M5個組,由于不同型號戰斗部對跑道的毀傷能力相差很大,機場搶修分隊搶修時的工作量差別也很大,故進行這樣的假設是必要的; ④各個修復分隊可并行作業,且修復彈坑的能力相同; ⑤每個搶修分隊修復彈坑的時間服從于(αω,βω)間的均勻分布。 3.2.2 彈坑修復時間建模 命題三已知隨機變量X的概率密度函數為fX(x),分布密度為FX(x)。今取出容量為ψ的樣本,分別記為{x1,x2,…,xψ},記Y為樣本中的最大值,則Y=max{x1,x2,…,xψ},記Y的分布密度函數為FY(y),則樣本的最大值的概率密度函數為 證明 FY(y)=Pu(Y≤y)=Pu(x1≤y,…,xψ≤y)= 故其概率密度函數為 當X服從均勻分布時,有: 經簡化得: (3) 證畢。 根據式(3),結合上述假設可以計算出重點搶修策略下的彈坑修復時間trp的概率密度函數。 ①如果M4≤M5,則: (4) 最后一輪修復時間的概率密度函數為 累計彈坑修復時間為 trp=M6trp1+trp2 (5) 由trp2 根據連續型隨機變量分布密度求取方法[15],可推導其概率密度函數為 (6) 根據3.2.1中的分析,跑道失效時間應為判定跑道損毀情況、確定應急跑道搶修方案、排爆作業和彈坑修復四部分時間之和,記判定跑道損毀情況時間為tdm,確定應急跑道搶修方案為tpl,排爆作業時間為twk,則有: tf=tdm+tpl+twk+trp (7) 式中:tdm和tpl均為定值。 由式(3)、式(6)和式(7)可推導得概率密度函數: 在機場遭受攻擊后,機場毀損情況判定系統完成判定所需時間tdm及機場確定應急跑道搶修方案需要時間tpl往往并不是固定的,這里,為簡化問題,都取其均值。如果能給定tdm、tpl的概率密度函數,可以根據隨機變量和的卷積公式,獲得更為精確的跑道失效時間tf的概率密度函數。 如果直接根據式(5),利用隨機變量和的卷積公式[15]來推導累計彈坑修復時間trp的概率密度函數,其結果非常復雜,因此,對最后一輪修復時間trp2進行了簡化處理。考慮到實際對抗過程中某些不確定因素的存在對跑道修復時間的影響,這種簡化是合理的。3 封鎖時間性能量度O2的映射
3.1 延時子母彈排爆時間的計算模型
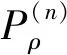
3.2 彈坑修復時間的計算模型
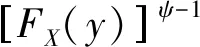
Pu(x1≤y)…Pu(xψ≤y)=[FX(y)]ψ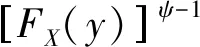
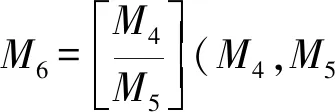
3.3 跑道失效時間的計算式
3.4 O2的分布特性
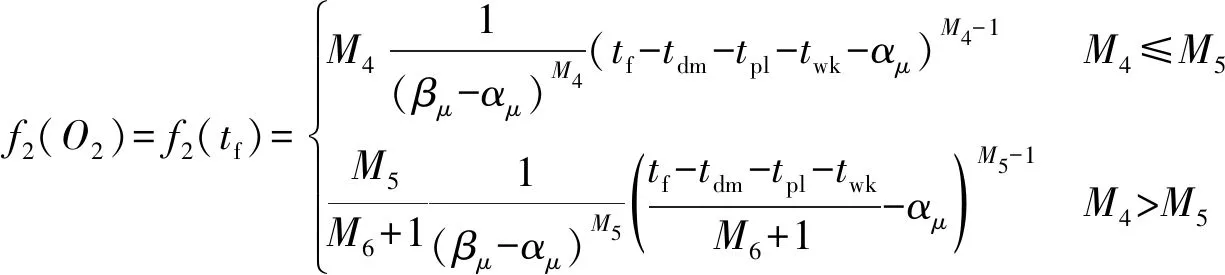
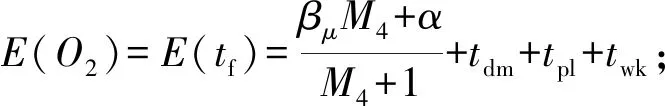
4 結束語

