火炸藥靜電感度試驗數理統計方法分析與優化

孫銘澤，王艷平，羅太明，饒云鵬，張騰月，曾 丹

(1.中國兵器工業火炸藥工程與安全技術研究院， 北京 100053；2.中國兵器科學研究院， 北京 100089)

引 言

靜電放電一直是火炸藥安全生產領域重點關注的安全風險因素之一，其放電火花可引起火炸藥燃燒或爆炸，繼而對火炸藥生產、儲運等過程造成潛在風險和重大安全隱患[1-5]。因此，火炸藥的靜電感度，或者靜電放電引燃的最小能量(Emin)，是表征火炸藥安全性能的重要參數之一。

由于靜電放電最小引燃能量(Emin)難以直接且準確地測量，加之環境因素影響具有隨機性和偶然性，故當前火炸藥的靜電安全特性主要通過靜電感度來表征，即火炸藥在靜電放電火花的作用下，發生燃燒或爆炸的難易程度[2,4]。

當前，靜電感度試驗主要基于數理統計方法設定試驗程序，開展系列靜電發火試驗，計算得到靜電放電能量與火炸藥響應概率的關系[7-12]。現行火炸藥靜電感度試驗標準[13-17]都采用升降法設定試驗程序，準確度較差，只能得到被試樣品50%響應概率所對應的靜電放電能量(E50)，不能準確測算極小概率(如百萬分之一)響應點，一定程度上影響了火炸藥靜電安全風險評估的準確性和有效性。

除升降法外，典型的感度試驗數理統計方法還包括蘭利法和最優化D法。蘭利法是一種變步長的升降法[9]，被應用于部分炸藥短脈沖起爆感度試驗方法和標準中，可快速得到50%概率感度數據；最優化D法屬于最優化方法[7-8]，操作和計算流程較為復雜，但試驗準確性較高，已被應用于美國感度試驗軍用標準。但因缺少相關研究驗證，蘭利法和最優化D法均未被應用于國內的火炸藥靜電感度試驗方法和標準之中。

因此，亟需開展基于不同數理統計方法的靜電感度試驗準確性研究，優選或改進現有數理統計方法，在最少試驗次數內，獲得更準確地火炸藥靜電感度分布，以提高對百萬分之一概率發火能量(E1ppm)等極小概率響應點的測算準確性，也能更準確地估計Emin等火炸藥安全性能參數。

本研究利用蒙特卡羅方法進行計算機模擬試驗對比，分析基于典型數理統計方法進行靜電感度試驗的特點，并對現有的蘭利法進行優化和改進，開展升降法、蘭利法、最優化D法以及優化和改進后的蘭利法4種方法的準確性研究，以期為優化火炸藥靜電感度試驗方法和標準提供理論依據，也為獲得更準確的火炸藥靜電最低引燃能量提供方法和途徑。

1 典型數理統計方法及對比分析

國內現行的感度試驗數理統計方法標準[18]中推薦了升降法和蘭利法等方法，美國軍用標準 MIL-DTL-23659D于2013年將最優化D法作為火炸藥感度試驗數理統計方法。因此，升降法、蘭利法和最優化D法都是目前國內外最具代表性的感度試驗方法，本研究將對這3種典型數理統計方法展開研究分析。

1.1 升降法

升降法最早由 W. J. Dixon 和 A. M. Mood 在1948年提出[5,10,12,19]，其流程簡單，是國內最常用的火炸藥靜電感度試驗數理統計方法。GJB/Z 377A-94對升降法的數據處理給出的均值計算公式為：

(1)

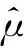
(2)

(3)

(4)

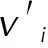
1.2 蘭利法

蘭利法由H. J. Langlie于1963年提出，并由Guillaume 在2010年補充了操作細節[20]，是一種變步長升降法，可快速得到50%概率感度數據，具有可操作性高的特點，試驗前只需提供全不響應刺激量xL作為試驗下限、全響應刺激量xU作為試驗上限，每次試驗點的計算只涉及簡單的四則運算。首次試驗時選擇上下限平均值作為初始靜電刺激量x0，隨著試驗次數增加，測點集中在感度分布均值處，可快速收斂獲得靜電感度分布均值，但不能準確測算分布方差，繼而影響了如E1ppm等依賴于方差的極小概率靜電引燃能量的測算準確性。

1.3 最優化D法

最優化D法是由Barry T. Neyer在1994年提出的一種基于Fisher信息矩陣的靜電感度試驗數理統計方法[7,8,21,22]，每次試驗前需先計算靜電感度分布，然后優化新的刺激量，使試驗后靜電感度分布的整體測算誤差最小，但每次試驗需要求解復雜的非線性優化問題，程序設定和計算十分復雜，操作難度大。此外，最優化D法需在預試驗后進行，Barry T. Neyer 最初提出的方法被稱為Neyer-D法，基于折半查找法進行預試驗[22]。華東師范大學的吳蔚[23]對其進行改進提出蘭利-最優化D法，可同時獲得較為準確的感度分布均值和方差，并對E1ppm等極小概率靜電引燃能量進行準確度較高的測算。因此，本研究選擇蘭利-最優化D法作為最優化D法的代表。

基于最優化D法進行靜電感度試驗時，若試驗次數較少時，則會因樣本不足以覆蓋極端情況而使測算的方差整體偏小，可通過引入大于1的偏量修正因子提高方差測算的準確性：

σC=β×σ

(5)

式中：β為修正因子，是試驗次數N的函數；σ為修正前方差；σc為修正后方差。本研究基于最優化D法開展不同次數的模擬試驗，計算得到靜電感度分布方差與設定真值之比作為偏量修正因子βi：

(6)

式中：Ni為模擬試驗次數；βi為Ni次模擬試驗對應的偏量修正因子；σi為Ni次模擬試驗后靜電感度分布方差測算值；σ0為靜電感度分布方差設定真值。將試驗次數Ni與對應的偏量修正因子與組合為數據對(Ni,βi)，并基于最小二乘法擬合得到最優化D法的偏量修正因子β與試驗次數N之間的數學表達式。

本研究分別基于修正前后的最優化D法進行不同次數的模擬試驗，不僅能驗證修正因子的有效性，也能分析基于該方法開展靜電感度試驗的特性。

2 蘭利法的優化和改進

針對蘭利法方差測算準確性不高的問題，本研究突破了原有方法測點集中在50%概率響應點附近的模式，探索性地提出將測點分散在30%概率和70%概率響應點周圍，以尋找被測樣品靜電感度分布的離散程度，從而更準確地捕捉分布方差。

基于改進的蘭利法開展靜電感度試驗的具體做法如下：

(1)試驗前設定全不響應刺激量xL作為試驗下限、全響應刺激量xU作為試驗上限，首次試驗選擇試驗上下限的算數平均值作為測點刺激量；

(2)在計算出的刺激量下進行靜電感度試驗，記錄第i次試驗的刺激量xi和響應vi后，從本次試驗開始往前查找歷史試驗記錄。

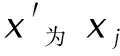
(4)若查找到j=1仍未滿足要求，則當vi=1時取定中間變量為xL，反之vi=0則取定中間變量為xU。

(6)重復步驟(2)～(5)，直至試驗次數滿足設定要求后，基于最大似然法計算靜電感度分布均值和方差以及不同響應概率臨界刺激量等結果。

當試驗次數足夠多時，符合條件的xj會接近樣品50%概率響應點，而中間變量取為其和試驗上限或下限的均值，則可有效地將測點分散在較小或較大概率響應點周圍，可比傳統蘭利法更準確地測算靜電感度方差。同時，改進后的蘭利法雖然操作上略復雜于原方法，但其每次測點建議值依然可通過簡單的四則運算得到，計算復雜度遠低于最優化D法。

基于改進的蘭利法進行靜電感度試驗時，也可根據(5)式和(6)式引入偏量修正因子減小方差的測算誤差。本研究通過模擬試驗，擬合得到改進蘭利法的偏量修正因子，并分別基于修正前后的改進蘭利法進行不同次數的模擬試驗，不僅能驗證修正因子的有效性，也能分析基于該方法開展靜電感度試驗的特性。

3 蒙特卡羅試驗研究方法與流程

蒙特卡羅方法是一種對隨機過程進行模擬后統計結果的計算機模擬試驗方法。本研究將通過蒙特卡羅法開展計算機數值模擬試驗，分析基于升降法、蘭利法、最優化D法、改進的蘭利法4種不同數理統計方法獲得結果的準確性，具體研究方法如下：

(1)設定初始刺激量x0=μ，步長d=σ，分別基于勘誤前后的升降法進行模擬試驗，對比勘誤前后結果的準確性；分別設定d=σ和d=σ/2進行模擬試驗，分析不同步長對升降法準確性的影響。

(2)設定試驗上下限為[xU,xL]=[μ+3σ,μ-3σ]，基于蘭利法進行不同次數的模擬試驗。

(3)基于最優化D法進行模擬試驗，擬合偏量修正因子；設定試驗上下限為[μ+3σ,μ-3σ]，對比有無偏量修正因子時，基于最優化D法進行模擬試驗的準確性；分別設定試驗上下限為[μ-3σ,μ+3σ]和[μ-2σ,μ+σ]兩種情況，基于最優化D法進行模擬試驗，對比分析試驗上下限對其準確性的影響。

(4)基于優化和改進后的蘭利法進行模擬試驗，擬合偏量修正因子；設定試驗上下限為[μ+3σ,μ-3σ]，對比有無偏量修正因子時，基于改進的蘭利法進行模擬試驗的準確性；分別設定試驗上下限為[μ-3σ,μ+3σ] 和[μ-2σ,μ+σ]兩種情況，基于改進的蘭利法進行模擬試驗，對比分析試驗上下限對其準確性的影響。

(5)對比分析基于上述4種方法開展模擬試驗的測點選擇的有效性，靜電感度分布均值和方差的測算準確性，以及小概率響應點的測算準確性。

上述研究內容中開展模擬試驗的具體流程如下：

(1)設定靜電感度分布的真值，將其設為均值μ0=10，方差σ0=1的正態分布；

(2)按方法計算每次試驗的測點刺激量xi，并基于靜電感度分布真值計算響應概率，并生成試驗結果vi；

(3)設定模擬試驗的次數N，完成一組N次試驗后，根據測點刺激量x1,x2,…,xN和響應情況v1,v2,…,vN，基于所選方法計算靜電感度分布均值和方差的測算值μα、σα，其中α=1,2,...標記不同組模擬試驗；

(4)基于測算出的均值和方差計算1%、0.01%、10-4%等小概率響應點臨界刺激量：

xα(p)=μα+upσα

(7)

式中：μα、σα為第α組模擬試驗得到的靜電感度分布均值和方差；xα(p)為概率p響應點靜電臨界刺激量；up為概率p對應的標準配位數，例如u1%≈-2.33，u1ppm≈-4.75；

(5)重復步驟(2)～(4)進行M組模擬試驗后，統計分析靜電感度分布測算值與真值之間誤差的均值與標準差：

ΔXα=Xα-X0

(8)

(9)

(10)

式中：Xα為第α組模擬試驗測算結果(可為感度均值、方差或小概率響應點)；X0為對應設定真值；ΔXα為第α組模擬試驗測算誤差；ME(ΔXα)為第α組模擬試驗測算誤差均值；SD(ΔXα)為第α組模擬試驗測算誤差標準差；M為模擬試驗組數；

(6)計算模擬試驗測算結果誤差在約68.26%置信度(單σ)下的置信區間，并繪制誤差線圖：

ΔXU=ME(ΔX)+Z(1-p)/2SD(ΔX)

(11)

ΔXD=ME(ΔX)+Z(1-p)/2SD(ΔX)

(12)

式中：p為置信度；ΔXU為置信區間上限；XD為置信區間下限；ME(ΔX)為結果X誤差的均值；SD(ΔX)為結果X誤差的標準差;；Z為正態分布標準分數，為計算方便本研究將其取1對應約68.26%的置信度。

當靜電感度分布均值和方差測算誤差的均值和標準差相對較小時，小概率響應點臨界刺激量測算誤差的均值和標準差可由其計算得到：

ME[Δx(p)]=ME(Δμ)+upME(Δσ)

(13)

SD[Δx(p)]=SD(Δμ)+upSD(Δσ)

(14)

式中：μ、σ、x(p)和up的定義同式(7)；ME為其均值；SD為其標準差。因此，本研究在通過數值模擬試驗分析4種方法特點時只分析了靜電感度均值和方差。

試驗中需令M?N(將M取為100×N)，使單組模擬試驗不確定性帶來的誤差降低到可忽略，保證統計的有效性。此外，取不同的試驗次數N進行模擬試驗，研究試驗次數對結果準確性的影響，并將最大試驗次數取為1000。蒙特卡羅計算機模擬試驗的具體技術途徑如圖1所示。

圖1 蒙特卡羅計算機模擬試驗流程圖Fig.1 Flow chart of Monte Carlo computer simulation test

4 結果對比與準確性分析

針對升降法、蘭利法、最優化D法和改進的蘭利法進行蒙特卡羅模擬試驗的結果進行對比分析，具體見圖2。

4.1 升降法

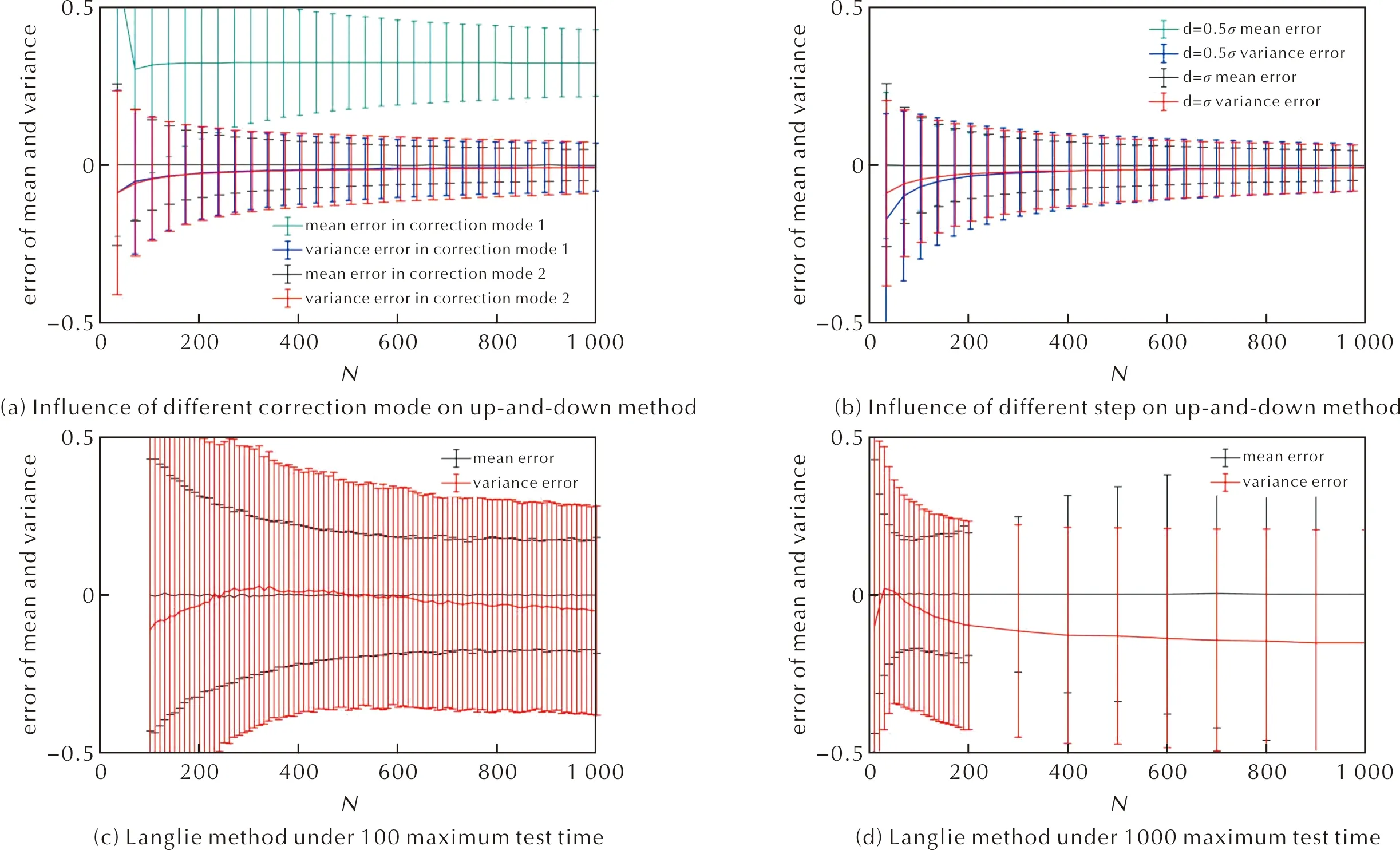
模擬試驗結果顯示，按照前文1.1中介紹的勘誤模式1的升降法進行模擬試驗，當試驗次數達1000次時，絕對誤差的統計平均值仍有約+0.32；而經前文1.1中勘誤模式2的升降法對靜電感度分布均值和方差的測算都較準確，誤差統計平均值幾乎為0，且測算誤差隨試驗次數增加而降低，如圖2(a)所示，圖2和圖3中的所有子圖均以誤差線的形式展現測算誤差，因此，本研究采用模式2對GJB/Z 377A-94中介紹的升降法勘誤；此外，當步長設定為靜電感度分布方差真值時，升降法的準確性尚可，但當步長設定偏離方差真值時，其在試驗次數較少時，對方差的測算誤差顯著增大，如圖2(b)所示。

因此，基于升降法進行試驗可對靜電感度分布的均值有效測算，得到較準確的50%響應點，但對方差測算誤差較大，所以無法獲得準確的極小概率響應點；而且升降法測試結果的準確性依賴于初始步長設定，穩定性較低。

4.2 蘭利法

模擬試驗結果顯示，基于蘭利法進行靜電感度試驗時，在約40次試驗內可以快速獲得較準確的靜電感度分布均值；但隨著試驗次數增加，試驗中的靜電刺激量會聚集在測算出的50%概率靜電響應點處，無法獲取其他響應點信息，導致測算誤差隨試驗次數增加反而增大，如圖2(c)和(d)所示。此外，蘭利法和升降法類似，只對靜電感度分布均值測算較準，而對方差的測算誤差較大。

4.3 最優化D法

根據模擬試驗結果，可擬合最優化D法偏量修正因子表達式：

(15)

式中：β為修正因子；N為試驗次數；a為擬合參數。模擬試驗結果顯示，基于最優化D法進行靜電感度試驗可同時準確獲得其分布均值和方差，且偏量修正因子會顯著降低100次試驗以內的方差的測算誤差，如圖2(e)所示，只有100次試驗內修正前后的感度分布方差測算誤差有所區別，其他上下限條件下的結果幾乎在圖像上重合，如圖2(f)所示，說明上下限取值對最優化D法獲得的靜電感度分布測算誤差無明顯影響。

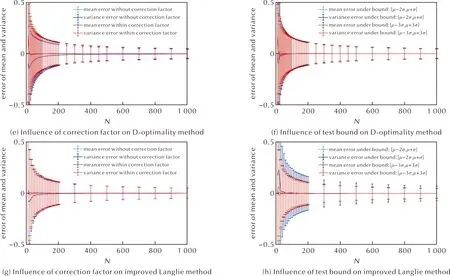
圖2 四種數理統計方法在不同情況下試驗結果測算誤差對比Fig.2 Comparison of the test result error under different conditions by four different mathematical statistical methods

因此，引入偏量修正因子后，最優化D法對靜電感度分布的均值和方差可同時準確測算，且結果準確性不依賴于試驗上下限的選取，穩定性較高。

4.4 改進的蘭利法

根據模擬試驗結果，可擬合改進的蘭利法偏量修正因子表達式：

(16)

式中：β為修正因子；N為試驗次數；a,b為擬合參數。模擬試驗結果顯示，基于改進的蘭利法進行靜電感度試驗，也可同時準確地測算分布均值和方差，修正因子可有效改善100次試驗內方差測算的整體偏差，如圖2(g)所示，只有100次試驗內修正前后的感度分布方差測算誤差有所區別，其他情況下修正前后的數據線在圖中重合。此外，上下限選擇會影響改進蘭利法的測算結果，特別是方差測算結果準確性，但其穩定性依然優于原始的蘭利法，如圖2(h)所示。

因此，引入偏量修正因子后，改進的蘭利法可憑借遠低于最優化D法的操作難度和計算復雜度，對靜電感度分布均值和方差同時進行準確測算，只是穩定性略差于最優化D法。

4.5 方法準確性對比與分析

首先，對比4種不同方法試驗的測點分布：升降法測點集中在靜電感度分布均值及其兩側；蘭利法測點聚集在均值附近；最優化D法的測點分散在約15%和約85%概率響應點兩處；而改進的蘭利法測點均勻地分散在約30%概率和約70%概率響應點周圍，如圖3(a)所示。

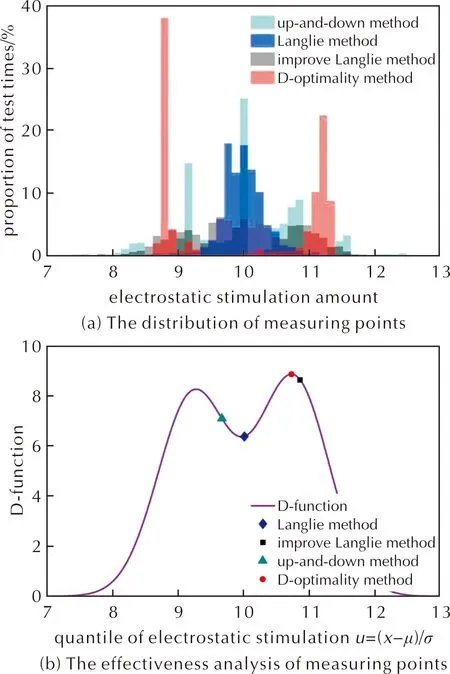
圖3 不同數理統計方法測點對比分析Fig.3 Comparison and analysis of measuring points with different mathematical statistics methods

利用Fisher信息矩陣的行列式，即D函數，可評估試驗中測點選擇的有效性。在測點位置進行一次新的試驗后，靜電感度分布測算誤差矩陣的行列式等于D函數的倒數，可反映測點對靜電感度分布準確測算的有效貢獻。結果顯示，從蘭利法、升降法、改進的蘭利法到最優化D法，D函數遞增，測點選擇有效性依次增加，如圖3(b)所示。

其次，對比不同方法對靜電感度分布均值與方差的測算誤差。結果顯示，與均值為10和方差為1的設定真值比較，升降法、最優化D法和改進的蘭利法對靜電感度分布的測算誤差均隨試驗次數增加而降低；升降法對均值的測算誤差尚可，但對方差的測算誤差最大；蘭利法能快速測算出較準確的均值，但試驗次數增多后測算誤差反而增大；優化和改進的蘭利法對均值與方差的測算誤差均尚可；最優化D法表現最佳，對均值和方差的測算誤差均最小，如圖4(a)和(b)所示。

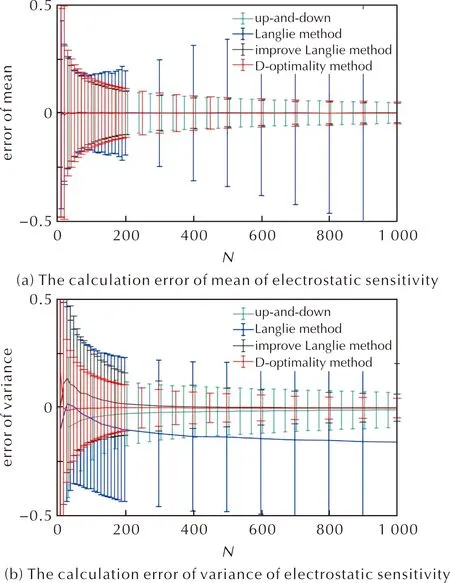
圖4 不同數理統計方法均值和方差誤差對比Fig.4 Comparison of measurement errors of mean and variance by different mathematical statistics methods

僅從均值和方差的測算上考慮，優化和改進后的蘭利法和最優化D法的準確性難分伯仲。因此，進一步分析其對小概率響應點的測算準確性，與百萬分之一、萬分之一和百分之一3個小概率響應點的設定真值(約5.245、6.28、7.67)比較，各方法的測算誤差如圖5所示，典型試驗次數下百萬分之一概率響應點的測算結果的測算誤差對比如表1所示。

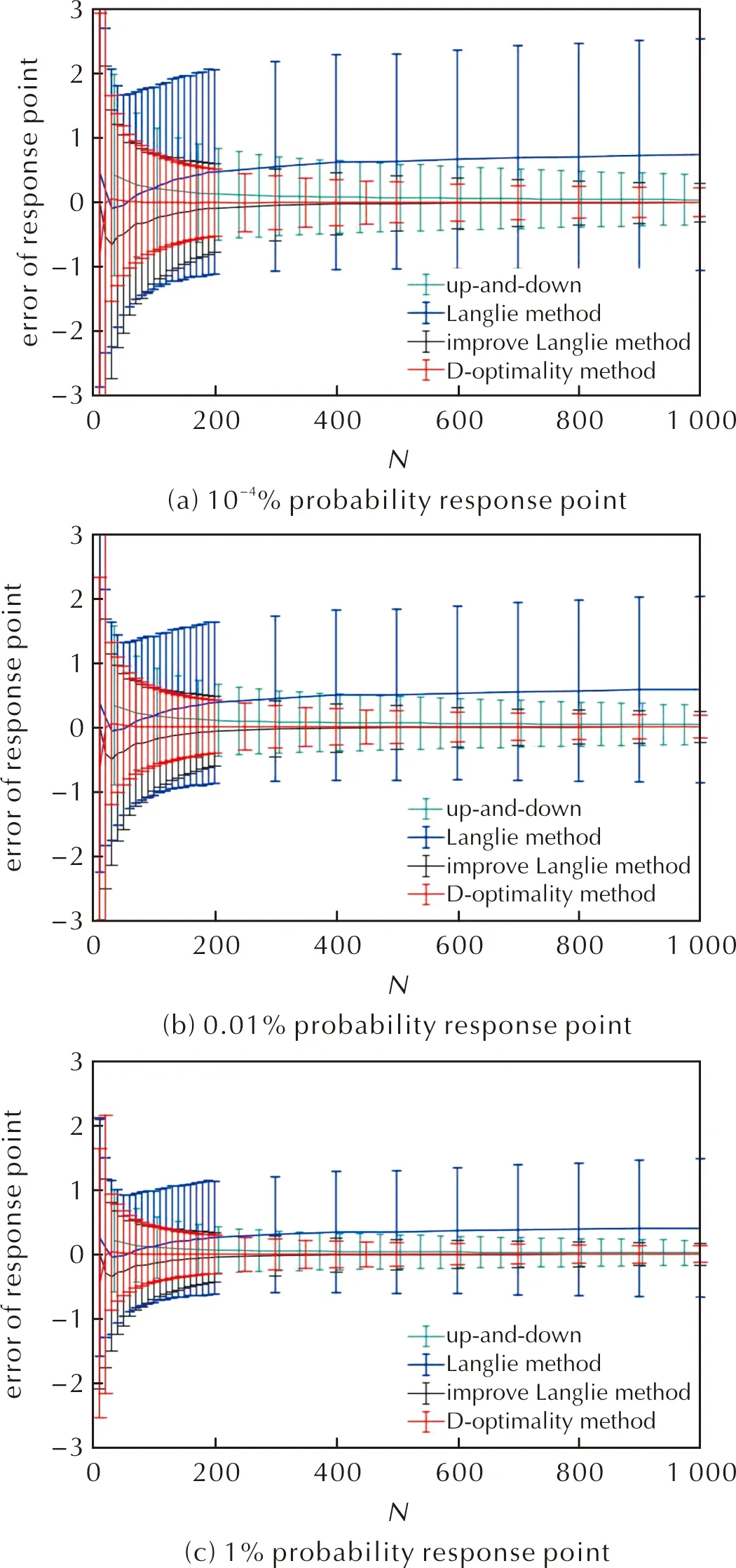
圖5 不同數理統計方法小響應概率點結果比較Fig.5 Comparison of results of small response probability points of different mathematical statistics methods

表1 典型試驗次數下10-4%概率響應點測算誤差68.26%置信區間對比Table 1 Comparison of 68.26% confidence interval of 10-4% probability response points error under typical test times

結果顯示，最優化D法對小概率響應點的測算準確性優于改進的蘭利法，其在較少的250次試驗內，可將E1ppm的測算誤差的68.26%置信區間控制在0.456以內，使其相對誤差小于10%。綜上所述，最優化D法是四種數理統計方法中最適合靜電感度試驗的方法；優化和改進的蘭利法具有操作便捷的優點，試驗中的計算復雜度遠低于最優化D法，其將測點集中在較小和較大概率響應點的改進思路，可為進一步優化靜電感度試驗數理統計方法提供參考。

5 結 論

(1)通過蒙特卡羅法計算機模擬試驗，分析了基于現有典型數理統計方法進行靜電感度試驗的特點：升降法操作最簡單，可對靜電感度分布均值和方差進行較準確測算，但對初值和步長選擇敏感，穩定性差；蘭利法也具有操作簡單的特點，可快速獲得分布均值，但對方差的測算誤差較大；最優化D法操作難度和計算復雜度較高，但對感度分布均值和方差測算準確性和穩定性都最高；增加試驗次數可提高升降法和最優化D法的測算準確性。

(2)對比研究發現：最優化D法可在較少的試驗次數內最準確且穩定地測算靜電感度分布，在250次試驗內可將E1ppm的測算相對誤差的68.26%置信區間控制在10%以內，能準確表征火炸藥靜電最低引燃能量，為火炸藥靜電安全風險的定量化分析提供基礎數據。但其使用過程需要進行大量復雜數學計算，試驗時對人員技術能量要求較高，不適合作為常規靜電感度試驗的方法，未來可研發專用試驗程序軟件，自動完成復雜的測點刺激量計算和試驗結果計算等過程，輔助操作人員基于最優化D法開展靜電感度試驗。

(3)優化和改進后的蘭利法，突破了傳統靜電感度試驗方法測點集中在50%概率響應點的思路模式，將測點分散在約30%和約70%概率響應點周圍，在程序設定和計算復雜度遠低于最優化D法的同時，達到與其相似的準確性。

(4)提出的分散測點的思路可有效測算方差的準確性，可作為未來進一步研究靜電感度試驗方法和程序的基礎，以期建立一種新的感度試驗數理方法，在提高極小概率響應點測算準確性的同時，具有較為簡單、可操作性強的特點，方便用于常規靜電感度試驗。