某航空密封件波形彈簧力學性能分析

袁紅彬，陳康文，田井文

（中國航發長江動力有限公司，湖南 岳陽 414100）

波形彈簧主要應用于飛機和發動機附件傳動系統、發動機主氣流通道和二次氣流通道以及主軸支點軸承滑油系統、直升機傳動系統的密封組件中作為彈性補償件以保證主密封副的貼合，是航空用密封件產品的重要組成部分。彈簧結構為帶有若干個正弦波形（單層或者多層）環件，相較于傳統彈簧，波形彈簧的變形能是由波峰波谷的變形存儲，軸向或徑向尺寸普遍較小，擁有更好的儲能、緩沖、減震和降噪能力[1-4]。其中，單層波形彈簧被廣泛地應用在載荷和變形都比較小的工作場合，同時因為其擁有相對較為穩定的剛度特性曲線，因而也常被使用在對精度有特殊需求的場合，如當前航空發動機中常見的石墨端面密封結構，采用的就是用單層波形彈簧為主密封副提供補償力，進而達到密封效果。

目前國內外研究主要集中于彈簧的新結構設計、熱處理工藝、殘余形變或模態計算等方面。如汪潭[5]通過材料力學的彎曲梁模型理論方法對波形彈簧單個波形進行簡化，以單個波峰為中心的半波進行簡化、分析以及彈力計算，得到波形彈簧彈簧力的計算公式。周文鳳等[6]利用工裝以及回火熱處理控制工藝提高波形彈簧的合格率。王振春等[7]則對波形彈簧的加工工藝進行了研究探討，確定最佳工藝路線并優化模具結構。學者們對波形彈簧加工工藝以及新型結構設計優化[8-11]等方面均有所建樹。然而，設計研究方向較為分散，目前市面上波形彈簧產品質量參差不齊，彈簧的力學性能差，穩定性難于保證等問題普遍存在，對波形彈簧承載特性受結構參數影響的研究相對較少，波形彈簧的研究還需要更加深入具體。

因此，本文以有限元方法探討分析波寬、波厚和自由高度等結構參數對波形彈簧力學性能的影響。利用正交分析提取了承載特性的敏感因子，并基于有限元分析結果，采用0Cr17Ni7Al 高溫合金環坯進行回彈試驗，旨在驗證模型的可靠性。為波形彈簧的結構設計與優化提供參考。

1 有限元模型建立

基于ABAQUS/Explicit 軟件平臺建立了如圖1所示的液壓有限元模型，建模過程中解決了以下關鍵技術。

圖1 波形彈簧有限元模型

1）網格處理：上下模具設定解析剛體，不用劃分網格，以便于減少計算時間。波形彈簧網格類型選擇為C3D8I，進一步降低計算成本，尺寸為0.1 mm，元素總數為27 684。

2）摩擦邊界條件處理：彈簧在下壓以及回彈過程中，摩擦因數取0.15。波形彈簧材料設為彈塑性材料，材料塑性變形服從Mises 屈服準則，彈性模量符合楊氏模量。

3）材料設定：本研究中波形彈簧材料為0Cr17Ni7 Al 不銹鋼，其物理性能見表1。

表1 0Cr17Ni7Al 物理參數

5）運動軌跡控制：選取下模施加固定約束后再進行摩擦約束及壓縮設置。設置上模僅延Y 方向運動，總行程為1.8 mm 工作高度，完成波形彈簧的下壓和回彈的工作過程。考慮到波形彈簧在軸向上存在幾何非線性，因此在分析步的設置中打開幾何非線性。如圖2 所示。

圖2 波形彈簧有限元模型

2 結果與討論

2.1 有限元模擬條件與評價指標

波形彈簧主要結構參數為彈簧的內徑Dn、外徑Dw、厚度δ、波數N 和自由高度H 等。

具體建模公式如下

本研究中所模擬的對象直徑為φ80 mm，自由高度4.8 mm，厚度0.4 mm 的0Cr17Ni7Al 高溫合金單層波形彈簧下壓以及回彈過程，彈簧的具體結構參數見表2。

表2 0Cr17Ni7Al 彈簧的結構參數

2.2 有限元模擬結果分析

2.2.1 剛度計算

研究采用仿真計算、理論分析以及試驗檢測方法研究波形彈簧的剛度變化。3 種方法所得剛度特性曲線如圖3 所示。由波形彈簧剛度以及結構建模計算公式可知，其材料厚度、徑向寬度和自由高度等均對彈力性能造成直接性影響，因而分別將這幾個參數作為剛度影響因素進行承載特性分析研究，確認其影響規律。

其中，剛度理論計算公式為

式中：K 為理論剛度值；N 為波數；D0與Di分別為彈簧外徑和內徑，mm；t 為彈簧厚度，mm；K*為徑向位移修下系數[2]。

由圖4 可知，數值分析計算與試驗擬合度較高，說明了本研究中波形彈簧的仿真計算值真實可靠。仿真結果與測試數值均表現出軸向載荷與軸向壓縮量呈現近線性狀，這意味著在常溫條件下該型號的0Cr17Ni7Al 波形彈簧在壓縮量0～1.8 mm 工作范圍內軸向剛度基本保持不變。

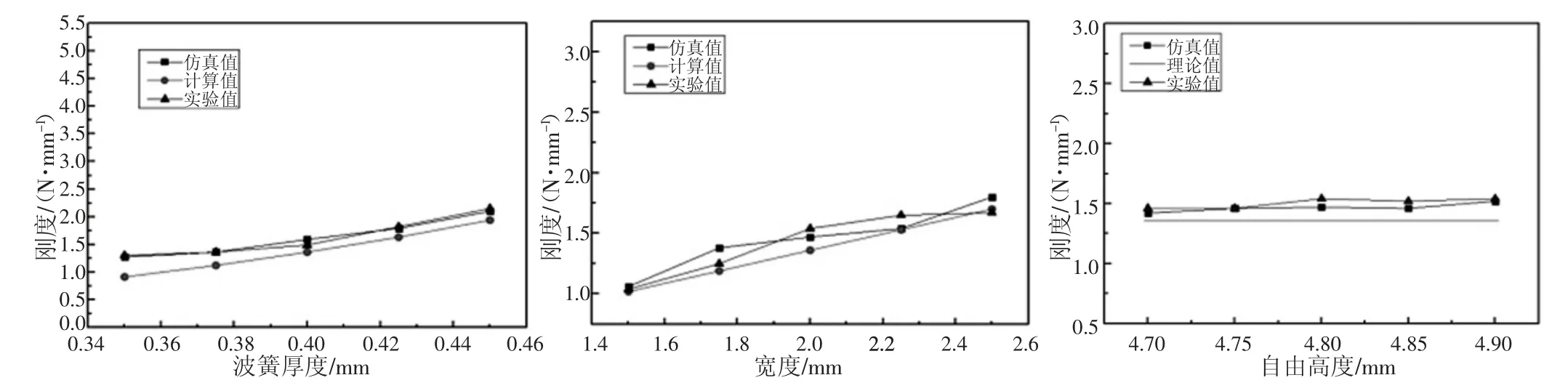
圖3 波形彈簧結構參數對彈簧剛度的影響

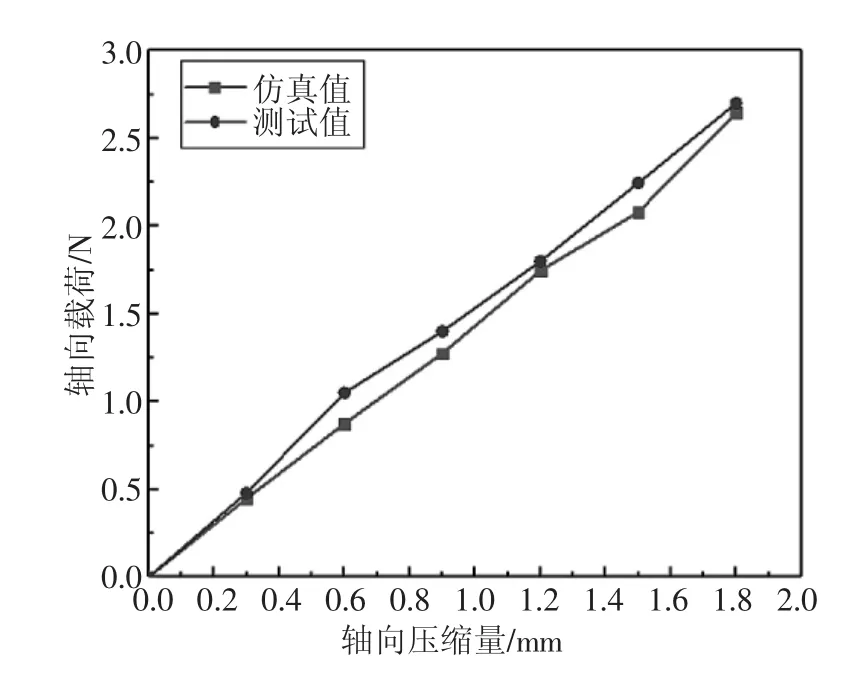
圖4 波形彈簧剛度分析曲線

此外，如圖3 所示，0Cr17Ni7Al 波形彈簧的剛度理論值、實驗值以及仿真值均表現出隨著波形彈簧材料厚度、寬度的增大而增大，然而自由高度變化則對波形彈簧的剛度值影響較小。因此在實際設計過程中，在保持波形個數不變基礎上通過調節波形彈簧的厚度以及寬度可以有效地改變波形彈簧設計剛度。

2.2 最大等效應力

圖5 是波形彈簧壓縮至1.8 mm 工作高度時，其厚度、寬度以及自由高度對最大等效應力影響。可以看出，隨著波形彈簧厚度、寬度以及自由高度的不斷增大，波形彈簧的最大等效應力均呈現出線性增加趨勢，其數值也都低于0Cr17Ni7Al 不銹鋼材料的屈服值，這說明波形彈簧在工作高度范圍內使用不會產生屈服現象。同時可以注意到材料厚度以及波形彈簧寬度所帶來的Von-Mises 增加幅度值則出現逐漸下降趨勢，這與自由高度變化所帶來的最大等效應力變化幅值趨勢不一致。部分學者認為[12]，這是由于波形彈簧寬度的增加會一定程度上減少其在壓縮過程中應力集中的產生，從而導致了最大等效應力增加幅度有所下降。

圖5 波形彈簧結構參數對彈簧最大等效應力的影響

3 極差分析

波形彈簧的承載特性受到多因素綜合影響，通過正交實驗法可研究承載特性敏感因子，能夠在設計過程中有效地優化波形彈簧結構，找出最好的特性參數組合，為波形彈簧的設計與優化提供數據支撐。正交實驗通過利用規格化的正交表來設計多因素的試驗方案以達到減少實驗次數獲得最優因素水平設計方法。

在本次研究中，通過正交試驗法來設計波形彈簧的壓縮回彈仿真試驗方案，用最短的時間完成最少的仿真次數，以便最快速得到波形彈簧的承載特性敏感因子排序，提高設計效率，具體變量因素組合見表3。

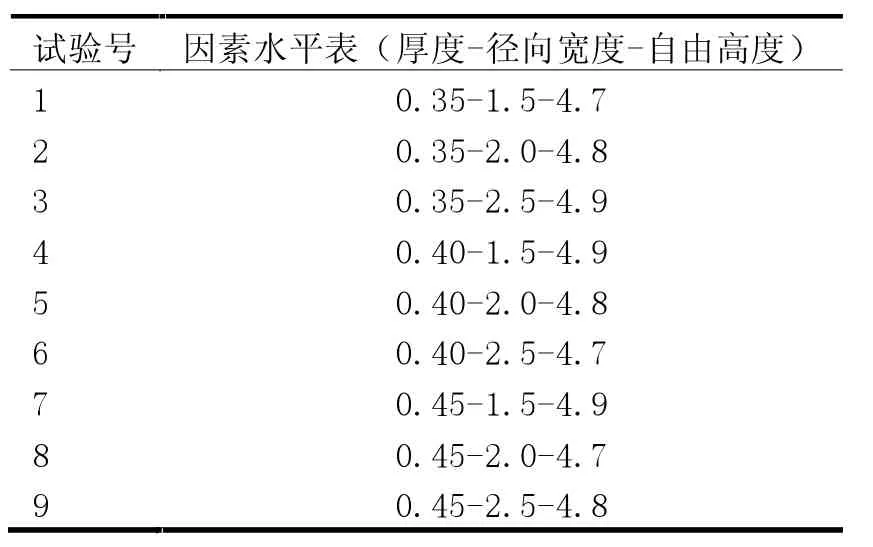
表3 0Cr17Ni7Al 彈簧的結構參數

以壓縮至工作高度為基，通過等效應力及剛度值結果比對可知，在波寬、波厚和自由高度等結構影響因素當中，最大等效應力對自由高度變化最為敏感，其次為波厚。波形彈簧剛度則對寬度變化最為敏感，其次為材料厚度，而自由高度變化相對影響較小，如圖6 所示。

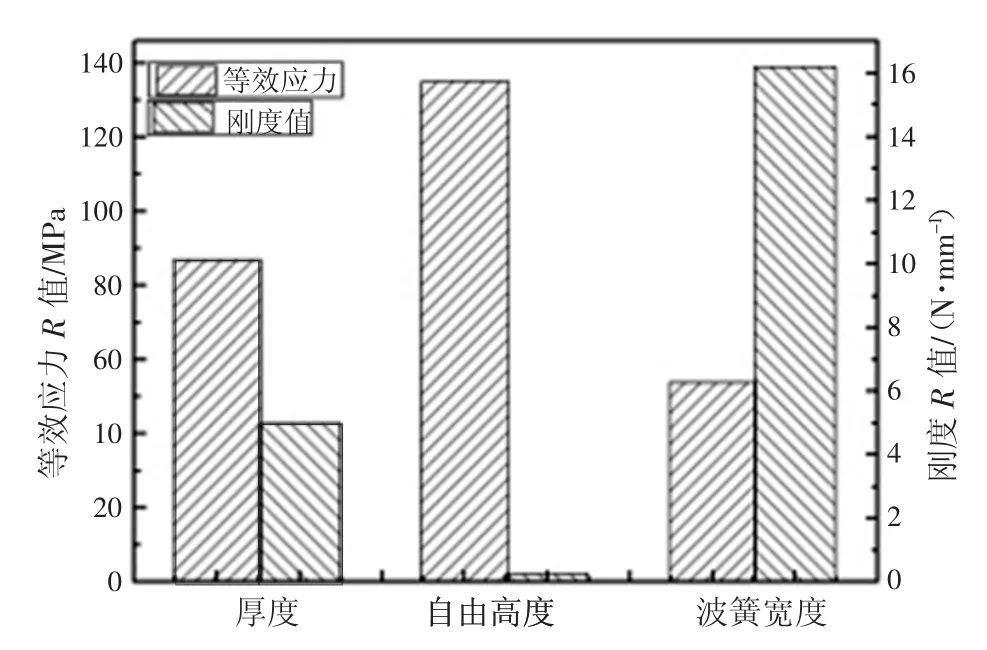
圖6 結構參數極差分析圖

4 結束語

通過對航空密封組件中精密彈性元件的波形彈簧力學性能研究，得出以下結論：①0Cr17Ni7Al 高溫合金，波數N 為3 的波形彈簧剛度隨著材料厚度、徑向寬度增加而增大，然而與波形彈簧自由高度變化則關系不大。②在常溫條件下該型號的0Cr17Ni7Al 波形彈簧在壓縮量0～1.8 mm 工作范圍內軸向剛度基本保持不變。③本研究中，波形彈簧隨著材料厚度、徑向寬度以及自由高度的增加，最大等效應力呈現出較為明顯的增大趨勢。④波形彈簧剛度以及最大等效應力對結構參數的敏感程度不一，最大等效應力對自由高度變化最為敏感，其次為波厚。而剛度則對材料寬度變化最為敏感，其次為材料厚度，自由高度變化則對剛度影響較小。