仿生撲翼齒輪組設計及動力學分析

徐 濤，丁長濤

（浙江工業職業技術學院 機電工程學院，浙江 紹興 312000）

面對工作任務復雜、環境多樣等原因，催生出一種新型的仿生撲翼機構，即在飛行方式上進行創新，而如何解決撲翼動力傳動問題是眾多學者需要攻克的難題。國外學者Saxena 等[1]研究了齒輪傳動轉子系統的動力學特性及嚙合剛度對齒輪轉子系統固有頻率和振型的影響。通過振動特性來檢測齒輪齒面故障，發現裂紋程度不同對齒輪轉子系統模態特性和頻率響應函數的影響。Yang 等[2]利用ANSYS 分析裝配線性模態求得齒輪系統頻率及模態振型，得知齒輪系統固有頻率位于2 個臨界狀態的頻率之間。崔永霞等[3]考慮齒面接觸應力大導致齒輪振動進而使齒輪失效損壞，對直齒圓柱齒輪在不同載荷、頻率激振下開展了諧響應振動分析，結果表明齒輪最大齒面接觸應力與激振頻率呈正比。李世慧等[4]考慮到齒輪體積、重量、數量增加及空間成本制約，基于MASTA 和Workbench 設計分析了在滿足輕量化標準下的行星齒輪箱的強度、動力學分析。Zheng 等[5]利用ANSYS Workbench 對齒輪泵進行接觸應力、模態分析，得知齒輪泵最大接觸應力位置即最容易發生疲勞失效的位置。Kadam 等[6]通過試驗模態分析發現直齒圓柱齒輪由于材料性能變化固有頻率改變，以此來實現齒輪的輕量化設計。何育民等[7]發現雙齒嚙合時有沖擊力產生且嚙合進出時振動會加劇使得振動強烈。Liu 等[8]建立了船用齒輪箱有限元模型，進行了模態分析及實驗對比，發現兩者吻合程度較高，最大頻率誤差為4.04%。王東升等[9]基于ANSYS Workbench 分析了齒輪箱箱體的動態響應特征，結果發現在激勵頻率為390 Hz 左右時箱體軸上部肋板發生共振的概率較大，在設計相關部件時應避開系統固有頻率。王園[10]基于變槳減速器的傳動原理對減速器齒輪的部位進行建模并在Workbench 軟件中開展靜力學分析。Fan 等[11]在SolidWorks 中建立了差速器的幾何模型并利用ANSYS 進行了強度校核和模態分析。結果表明，差速器齒輪副的最大應力模擬結果為624.14 MPa，齒輪副工作頻率遠低于第一固有頻率。Ericson 等[12]采用試驗模態對直齒行星齒輪的平面動態特性進行分析，并對有限元結果進行了對比。

已有研究僅通過單一角度考慮撲翼機構傳動，并未綜合考慮撲翼在真實飛行工況時所受外界因素影響。本文擬通過單驅動傳動機構實現撲翼多自由度運動，依據生物尺度率優化設計齒輪組結構并考慮真實飛行工況進行模態、諧響應分析，更加深入剖析齒輪組強度、應變、位移、頻響應狀態，為研制仿生樣機提供理論參考。

1 齒輪組模型設計

仿生撲翼機構采用雙曲柄雙搖桿機構配合齒輪減速機構以實現旋轉運動至拍打運動的轉換。而齒輪組配合對于撲翼運動平順可靠起到至關重要的作用，包括齒輪的尺寸參數、傳動比、體積重量、結構強度、疲勞極限及裝配體嚙合傳動和共振響應等。以中型鳥海鷗為原型，根據生物尺度率及展弦比設計齒輪組，參數見表1。

表1 齒輪組參數

根據齒輪組參數并基于SolidWorks 進行三維建模，同時考慮樣機整體質量且不影響整體結構強度將齒輪設計為輪輻式，三維模型如圖1 所示。

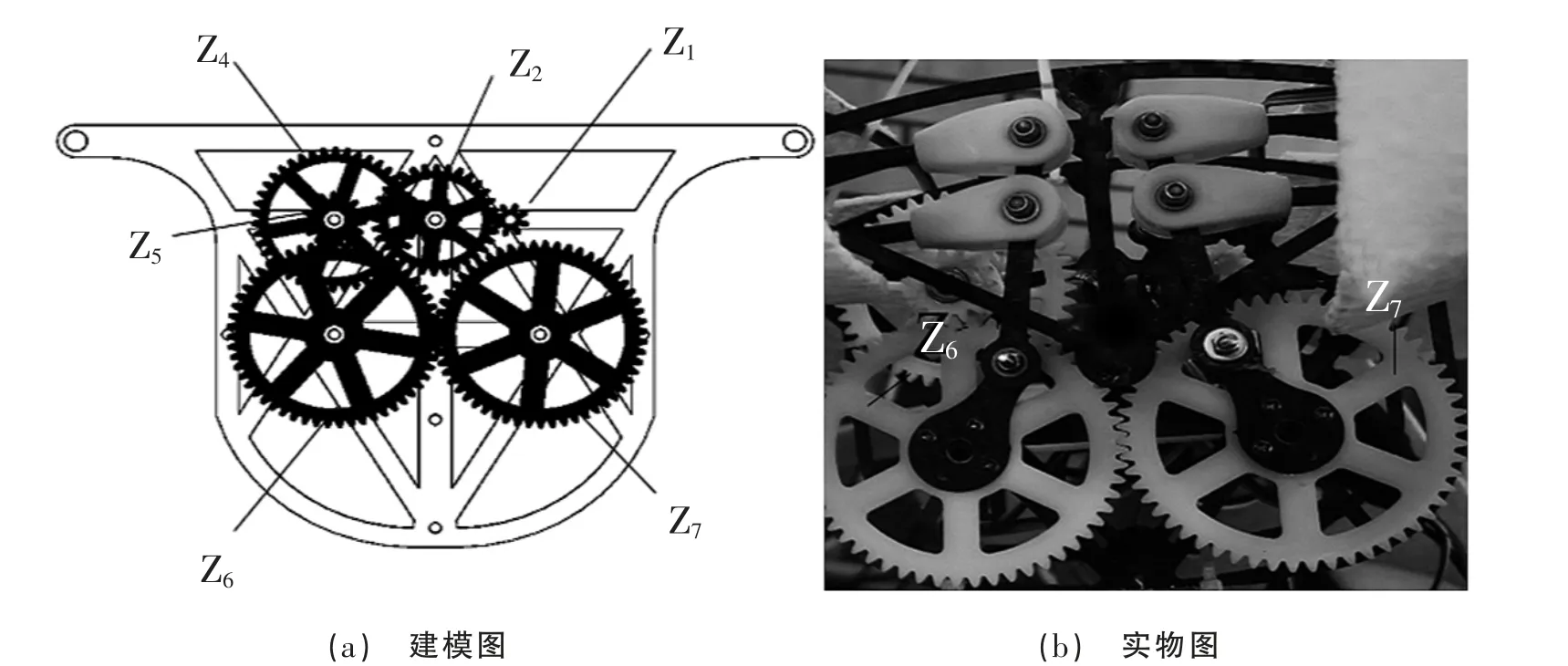
圖1 齒輪組模型

2 模態分析

2.1 理論計算及前處理

模態分析是動力學分析的基礎，固有特性對動態負載、響應及系統的振動形態均有重要影響。定義齒輪嚙合運動為扭轉振動模型將其等效為單自由度系統振動。系統分析模型由下式（1）（2）確定

兩式聯立，求解可得

由于Z6、Z7齒輪分別連接撲翼左右側曲柄搖桿機構，相對于傳動齒輪受力更加復雜，為了使撲翼實現多自由度運動在齒輪組中獨立離散出主動輪Z6、從動輪Z7進行分析，為了使得模擬更加接近工程實際，在模態分析預處理前對齒輪施加預應力。齒輪組采用自動非結構化網格模式，非結構化網格具有良好的延展性，計算周期短不浪費計算資源。由于齒輪組嚙合傳動接觸應力對模擬結果有較大影響，為了提高計算精度，對齒輪組嚙合傳動面進行網格加密處理。最終模型生成總網格數為60 841，節點數為10 806，最小網格在0.5 mm以上，求解計算采用Mechanical APDL，滿足計算要求。

2.2 結果分析

建立齒輪副需要分析齒輪節點嚙合的某一時刻對齒輪副建立摩擦接觸，接觸面為Z6齒面，目標面為Z7齒面，摩擦系數0.15。根據模型理論計算施加運動副載荷為10 N/mm，角速度為35.2 rad/s，齒輪固定孔施加預應力為1 MPa，設置完成后進行求解計算得到前18 階部分固有頻率值，見表2。

表2 前18 階部分固有頻率值

前18 階部分模態振型如圖2 所示，圖2（a）為第5階模態可以看出輪齒嚙合處沿z 軸方向發生彎曲但變形程度不明顯，在固有頻率125.83～1 032 Hz 激勵下，齒輪嚙合過程相對穩定，共振現象不產生。由于輪齒固定孔施加了固定約束，使得裝配體呈現由嚙合處向外延伸的折疊變形，變形區間值域在0.7～198 mm 之間；圖2（b）為第8 階模態振型沿y 軸方向的彎曲變形，振型與5 階類似但變形程度加劇；從第10 階模態、13 階模態發現齒輪發生了嚴重的彎曲扭轉變形且最大變形量均在齒面及齒根位置處,其值分別為283、370.85 mm。從圖2（e）發現第15 階模態振型是沿y 軸的反向大撓度彎曲但扭轉程度不明顯，變形程度由齒輪固定孔往圓周方向遞減再遞增的趨勢，呈“凹”狀。第18 階模態振型在輪齒嚙合處沿x 軸呈擠壓變形且整體型變量較大，齒根及齒面部分也完全重合過盈。

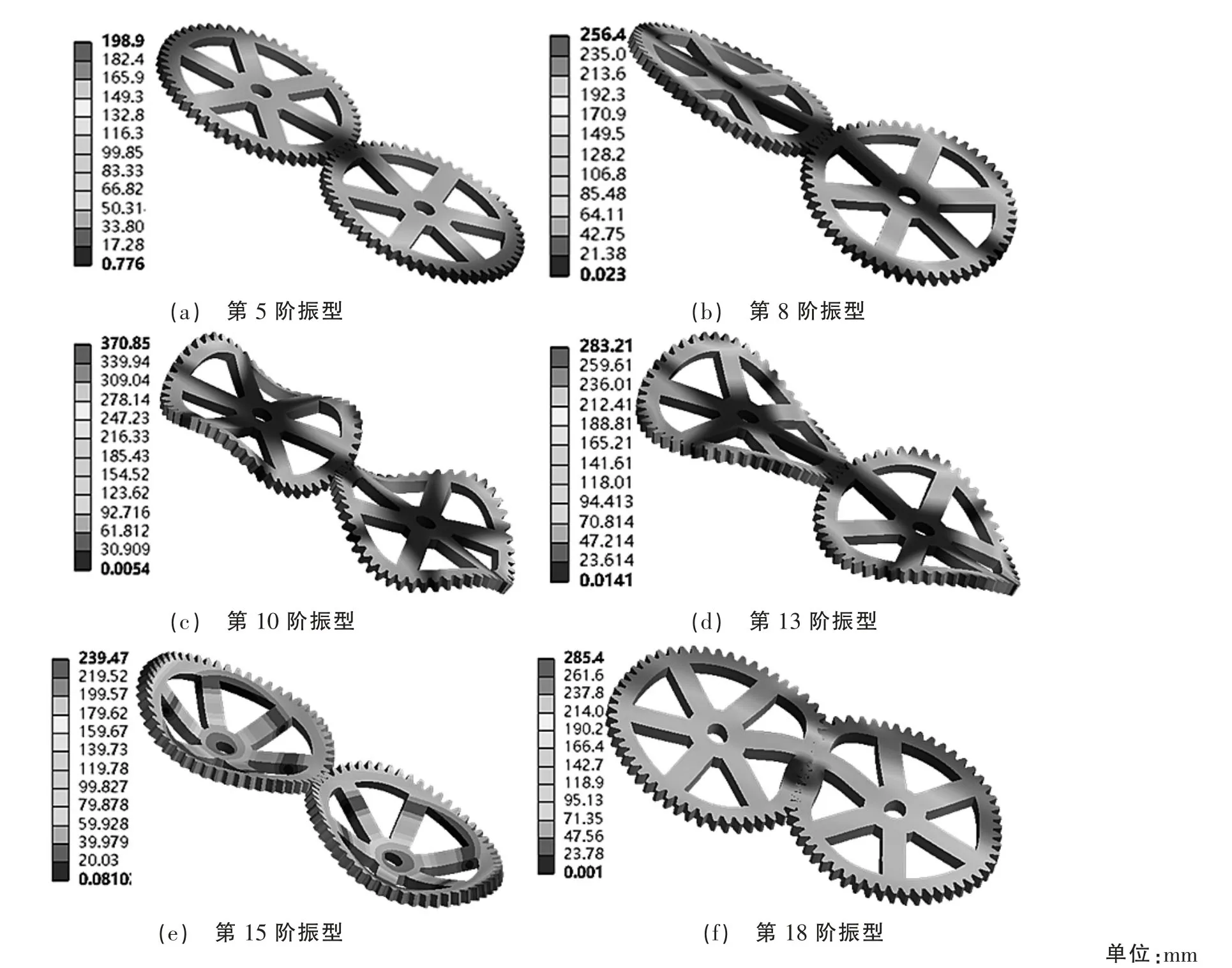
圖2 模態振型圖

從上述分析可知，齒輪傳動失效形式伴隨輪齒嚙合彎曲、扭轉和擠壓變形等，在滿足齒輪組結構強度、疲勞極限情況下應避開齒輪裝配固有頻率，避免因系統產生共振失效。

3 諧響應分析

模態分析研究結構得到動力學基本特性與結構所受載荷無直接聯系而諧響應分析可以在不同持續頻率的周期荷載作用下得到動力響應，計算結果與載荷直接相關，可以放大模態中不明顯的頻響特性。所受載荷為周期性簡諧載荷從而可知外界激勵頻率與固有頻率達到共振時模型振幅的具體參數。齒輪諧響應分析基于Workbench Harmonic Response 模塊開展，計算采用模態疊加法即通過線性疊加各階模態振型求得系統響應。雖然計算周期較長，但頻率響應會更精確地反映出模型固有特性頻率。

阻尼系數為0 及阻尼系數為0.05 的齒輪組嚙合等效應變如圖3（a）、（b）所示，由圖3（a）可知等效應變值域范圍在0.014～348.2 MPa 之間，整體應變較小且無突變遷躍。由于施加了固定約束限制了齒輪x 軸向自由度，應變較大區域出現在齒輪嚙合面及齒輪固定圓孔處，最大應變出現在齒根部位。圖3（b）發現應變值有降低趨勢，值域范圍在0.017～323 MPa 之間，平均應力在50 MPa 左右，比無阻尼狀態幅值降低約7.2%且應變區域明顯減少。

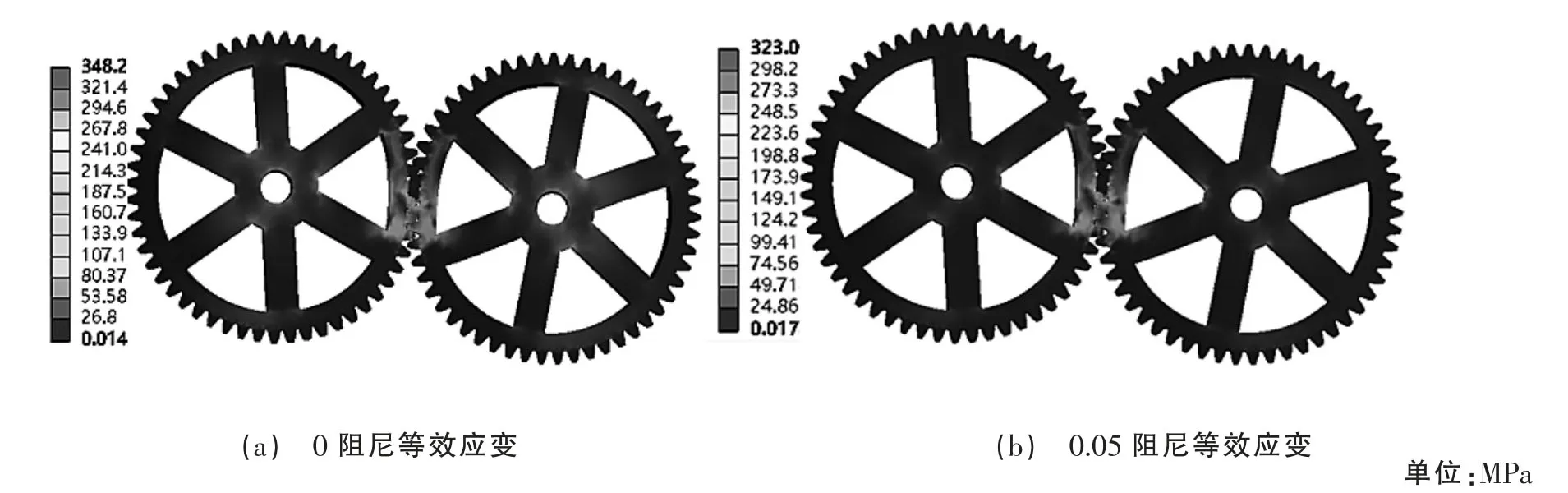
圖3 不同阻尼系數應力變化

圖4（a）、（b）為齒輪組形變位移圖，可知整體形變量較小，值域范圍在0.004～0.06 mm 之間，不同阻尼系數下區別不大，比無阻尼狀態幅值降低約3.1%且形變趨勢基本相同，均從主動輪坐標系左側逐漸遞增至右側方位，從動輪反之。齒面處呈最大形變，整體表現為擠壓形態。

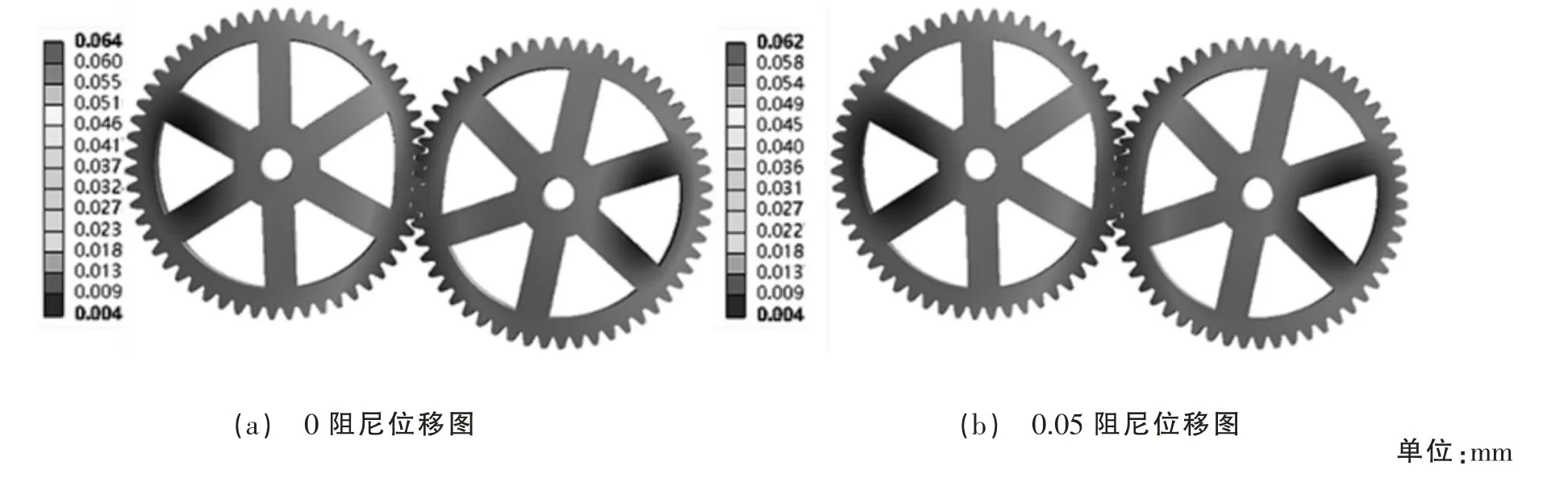
圖4 不同阻尼系數位移變化

基于模態疊加法的諧響應分析對頻率的選取范圍至關重要。將模態的頻率為諧響應分析的1.5 倍即設置計算頻率為0～6 000 Hz，每60 Hz 計算1 次，計算步長為100 次。為了更加直觀清晰地表明齒輪嚙合過程中不同頻率下的動態響應，節點隨頻率位移、相角變化如圖5 所示。其中細點線表示阻尼系數為0 時的頻率-位移變化曲線，粗實線表示阻尼系數為0.05 時的頻率-位移變化曲線。由圖5（a）發現，在850 Hz 激勵下節點位移達到最大值，為0.026 mm；頻率分別在3 600 Hz、3 800 Hz 時位移曲線出現不同程度的“尖峰”，當頻率為5 600 Hz 時位移再次達到最大值。對比模態分析發現，諧振激勵均發生在固有頻率附近，且低階頻率突變多于高階頻率，低階比高階頻率對系統的振動特性影響較大，而減小共振現象發生需避開其固有頻率。而當增加阻尼系數后發現曲線整體較為光順且多個峰值消除，平均位移約0.035 mm，在節點頻率為3 600 Hz 時位移降低程度最大為47.8%，但在低階頻率時最大位移值幾乎沒有改變。

由圖5（b）分析可知，無阻尼狀態下在多個頻段存在相位突變，當掃頻區域在60～850 Hz、3 600～4 000 Hz時，存在180°相位差的持續峰，在1 700 Hz 附近僅存在1 個180°相位差的尖峰。當阻尼系數增加時曲線變化更加平滑，除低階頻率波動外其余階段變化較小，平均相位范圍保持在100°左右，整體表現較為穩定。

圖5 諧響應變化曲線

由圖6 可知，在放大掃頻角度為720°下850 Hz激勵頻率的歸一化向量發現，不同阻尼系數的頻響特性有所不同，無阻尼狀態時y 向、z 向完全重合，x 向為0；增大阻尼系數可以使得動態響應狀態發生偏移，y 向、z 向偏移約為一個掃頻60 Hz，避開了共振激勵頻率。

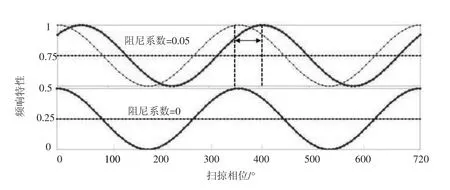
圖6 不同阻尼系數掃頻變化

4 結束語

本文設計了一種仿生撲翼機構齒輪組結構，基于Workbench 展開模態及諧響應分析，得到了齒輪組的等效應變、形變、固有頻率及頻響應特性，驗證了模型結構合理性，為仿生樣機研制提供理論支持。

1）齒輪嚙合前18 階模態振型發現低階頻率下齒輪變形不明顯，振型多為彎曲、扭轉變形；在7 階模態時頻率突變增幅達82%，而在1 711.5～9 439.1 Hz 激勵下齒輪出現擠壓、彎扭橫振的復雜變形。

2）通過諧響應分析對比不同阻尼系數發現，阻尼系數的增加可以降低齒輪局部接觸應力，減小應變范圍，比無阻尼狀態幅值降低約7.2%；可以降低齒輪位移變形，減小幅值約3.1%。

3）通過諧響應細化不明顯的頻響特性，分析齒輪嚙合各節點隨頻率變化位移、相位響應發現峰值均出現在固有頻率附近，進一步驗證了模態分析合理正確。在850 Hz 激勵下節點位移達到最大值，表明在齒輪設計時應避開固有頻率防止共振現象發生。