基于數值模擬的地鐵冷凝通風空調系統運行優化研究

付智杰

（中鐵第一勘察設計院集團有限公司 西安 710043）

0 引言

隨著社會經濟的進步與發展，我國城市現代化發展速度迅猛，公共交通等基礎設施建設量不斷增加，公共交通的便利性大大提升[1]。并且在全球氣候與環境問題日益突出的生態背景下，安全性高且污染較小的公共交通工具逐漸成為人們的日常出行交通方式[2,3]。地鐵作為城市公共交通系統的重要組成部分，運載量較高且快速便捷，在眾多城市得到了快速發展。但是地鐵系統的運營能耗較高是制約地鐵發展的重要影響因素，而地鐵的空調系統能耗在非牽引能源消耗中的占比超過一半，要求在滿足地鐵運行需求和人員舒適性的條件下，降低地鐵的運營能耗[4,5]。因此，研究為了地鐵冷凝通風制冷空調系統的能源消耗，通過數值模擬的方式，提出地鐵空調系統的低能耗運行優化模型，期望進一步提升地鐵空調系統的節能性。

1 數值模擬下的地鐵冷凝空調系統運行優化

1.1 地鐵冷凝空調系統建模

對地鐵冷凝空調系統進行分析，首先對地鐵冷凝空調系統進行數學建模，求解空調系統在不同空氣、負荷參數下的總功率，為地鐵空調系統運行優化提供參考。空調系統的壓縮機是制冷的重要部件，通過對制冷劑進行擠壓操作，促使制冷劑的流動和形態變化[6,7]。研究結合制冷機狀態參數、排氣量等參數構建壓縮機的效率模型，并將壓縮運行過程近似轉換為熱力學多變過程。在考慮電機損失的情況下，空調系統壓縮機的功率如式（1）所示。

式（1）中，Wcom表示壓縮機的指示功率，ηei為電機效率，Ws為壓縮機運行過程中制冷劑等熵壓縮的做功，ηs表示等熵效率，mη和ηmo分別為壓縮機機械效率和電機效率。

空調系統蒸發器分為兩區，制冷劑在兩相沸騰區從兩相狀態蒸發轉為飽和氣體，然后在過熱蒸汽區經過加熱變為熱蒸汽[8,9]。因此研究采用分布參數法構建蒸發器模型，將兩區按照不同的標準分別劃分為若干微元體，兩相區以制冷劑的焓差變化為標準，而過熱區則以制冷劑的溫度變化為標準。在蒸發器建模過程中，不考慮管內制冷劑的徑向流動，而將其視為一維流動過程，不考慮管道的軸向導熱問題，并且假設管道內制冷劑分布處于均勻狀態。蒸發器空氣側的傳熱和傳質方程如式（2）所示。

式（2）中，Qe,a表示空氣側的熱換量，me,a表示蒸發側的空氣質量流量，he,a,in和he,a,out分別表示各個微元部分的進風和出風空氣焓值，We,a表示微元段的平均空氣含濕量，dh為傳質系數，d表示微分，Ae,a表示空氣側的換熱面積。

建立空調系統蒸發式冷凝器的分布參數模型，依據相態變化將冷凝器分為過熱區、兩相區和過冷區，過熱蒸汽在過熱區冷凝為飽和氣體，然后在兩相區冷凝為飽和液體，在過冷區進一步降溫最終進入節流閥。為了便于建模，不考慮流體的熱傳導和管壁軸向導熱，不考慮水平管的重力條件，并且在兩相區分析中使用平均空泡系數模型，平均空泡系數不發生變化。管道內部制冷劑與水膜的換熱方程如式（3）所示。

式（3）中，mr表示制冷劑的質量流量，hc,r表示微元部分的制冷劑的平均焓值，aw表示傳熱系數，Ac表示制冷劑側的換熱面積，Δtc,r-w表示冷凝溫度與水膜的溫度差。水膜與空氣之間的傳熱方程如式（4）所示。

式（4）中，aj表示當量換熱系數，Δtw-c,w,a為水膜與空氣的溫度差，Δhc,w,s-c,a表示水膜表面飽和濕空氣與空氣之前的焓差。

從空調系統風機的設備數據信息中獲得風機特性曲線，結合地鐵送風系統管網的特性曲線求解風機工況點，風機全壓如式（5）所示。

式（5）中，Qf表示風量，a、b、c均為常數。風機的軸功率計算函數如式（6）所示。

式（6）中，fη表示風機全效率。風機電動機功率如式（7）所示。

式（7）中，K表示儲備系數，dη表示電動機效率。

順序模塊法和方程求解法是仿真系統求解的常用方法，順序模塊法以系統的構成結構與特點為基礎，將按照一定的順序將系統各個模塊構建成一個系統模型，在假定初值后，從內層模塊開始對模型變量進行計算，直到達到收斂條件[10,11]。相較于方程求解法，順序模塊法的求解步驟清晰，并且調試難度較小，便于較快發現問題所在。因此研究采用順序模塊法求解制冷空調系統的模型，空調系統模型的計算求解流程如圖1所示。輸入系統模型的已知部件參數，并假定系統的蒸發、冷凝溫度和供水溫度，分別通過系統模型中的壓縮機、冷凝器等模塊計算地鐵冷凝空調系統的運行參數情況。

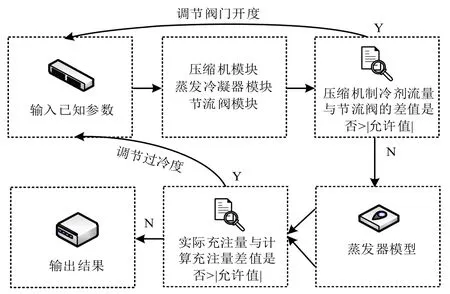
圖1 空調系統模型的計算求解流程Fig.1 Calculation and solution process of air conditioning system model

1.2 空調系統運行優化設計

研究以空調系統的數學模型分析為基礎，在約束條件下計算空調系統在不同運行工況下的系統能耗，并提出地鐵冷凝空調系統的運行優化模型，在保證系統效果的同時降低能耗。通過對空調系統設備的運行頻率下降控制，達到降低系統總能耗的目的，由于噴淋水泵在總能耗中的占比較小，而蒸發器側和冷凝側風機與壓縮機占比較大，因此以這三個設備的功率構建空調系統運行優化的目標函數，目標函數如式（8）所示。

式（8）中，Wzsf、Wfjp和WY分別表示蒸發器側風機、冷凝側風機與壓縮機的運行功率。系統運行優化需要以保證制冷量為前提，并且需要滿足系統的冷凝壓力條件和蒸發壓力條件。系統冷凝壓力，過高的冷凝壓力可能會導致制冷劑泄漏的問題，而過低的冷凝壓力會使得制冷量大幅下降，影響空調系統的制冷效果。蒸發溫度過高和過低都會引發壓縮機過載的問題，導致除濕效果降低或蒸發器結霜，因此需要保證系統的蒸發壓力保持在合理范圍內[12]。地鐵的冷凝空調系統除了控制室內溫度，還需要進行通風送風，因此需要保證系統的新風量滿足需求。以GB 157-2013 地鐵設計規范中的人均新風量要求為標準，設置系統優化的送風量條件。空調系統運行優化的約束條件如式（9）所示。

式（9）中，eQ表示制冷量，Pc表示冷凝壓力，Pe表示蒸發壓力，G表示送風量，nr表示停站瞬時人數。在建立的空調系統數學模型中輸入壓縮機頻率、蒸發器側和冷凝側風機頻率、室內冷負荷等工況參數，計算空調系統設備的運行功率和蒸發冷凝條件數據。通過計算空調系統在不同運行工況下的系統總能耗，并結合約束條件加以篩選，獲取系統總能耗最低情況下的各個設備運行頻率，建立地鐵冷凝空調系統的運行優化模型。由于地鐵站所需制冷量在實際運行過程中，難以進行實時準確預測，因此將運行優化模型與地鐵自控系統相結合，利用回風溫度對壓縮機進行調節，并結合冷凝溫度對風機進行調節，空調系統運行優化自適應控制流程如圖2所示。

圖2 空調系統運行優化自適應控制流程Fig.2 Adaptive control flow optimized for air conditioning system operation

2 空調系統運行優化效果分析

2.1 空調系統模型驗證

研究從某市隨機抽取20 個地鐵站制冷空調系統，采集地鐵站2019-2021年制冷季的歷史數據創建數據集，并從中選取35 個典型工況作為測試工況，對研究模型進行驗證分析。該市位于溫帶季風氣候區，隨機抽取的20 個地鐵站的平均建筑面積為18344.67m2，高峰期平均人流量為3658.29 人/h，平峰期平均人流量為1106.54 人/h，平均新風濕球溫度為22.6℃，平均制冷量為798.6kW。35 個測試工況的參數如表1所示。

表1 35 個測試工況參數Table 1 35 test condition parameters

對模型在35 個測試工況下的仿真模擬效果進行分析，不同工況下的模型壓縮機功率和制冷量誤差情況如圖3所示。

圖3 不同工況下的模型壓縮機功率和制冷量誤差情況Fig.3 Model compressor power and cooling capacity errors under different operating conditions

從圖3中可以看出，在不同的室內情況與室內制冷負荷條件下，模型的壓縮機功率仿真值與地鐵站實際值的差值較小，仿真誤差均保持在±10%以內，滿足工程設計計算的誤差要求。而從制冷量仿真值上看，研究所構建的模型制冷量仿真值與制冷實際量之間的誤差也均未超過10%，符合工程計算標準，證明研究模型能較好對地鐵站空調系統進行仿真模擬。為了保證系統運行優化模型的準確性，需要對模型的蒸發溫度和冷凝溫度進行驗證，由于蒸發和冷凝溫度難以直接進行測量，因此研究從模型的吸排氣溫度進行對比驗證，模型吸排氣溫度誤差對比情況如圖4所示。

圖4 模型吸排氣溫度誤差對比情況Fig.4 Comparison of model suction and exhaust temperature errors

從圖4（a）中可以看出，模型的吸氣溫度仿真值與實際溫度之間的誤差值較小，差值均小于1℃，出現誤差的原因可能是膨脹閥的開度較小導致過熱度偏高，高于設定值，使得最終吸氣溫度略高于實際值。從圖4（b）中可以看出，模型排氣溫度仿真值與實際值的誤差范圍不超過10%，平均仿真誤差值為3.26±1.42℃，滿足模型設計要求。由于壓縮機的排氣口無法直接布點進行數據采集，而將測試點布置在冷凝器，與壓縮機之間存在一定的距離，導致排氣溫度出現測試誤差。

2.2 運行優化效果分析

為了分析運行優化方對地鐵空調系統的實際優化效果，以地鐵站歷年數據中的最高制冷負荷情況為實驗工況，分析運行優化模型在實際地鐵制冷系統上的應用效果。根據歷年數據統計，地鐵站的最大制冷量為959kW，對應參數如表2所示。

表2 工況參數Table 2 Operating parameters

在最高制冷負荷工況下，使用研究所提出的運行優化模型分析最優工況點，剔除數據中制冷量不滿足要求、冷凝溫度過高、蒸發溫度過低等不符合約束條件的數據，蒸發器側風機頻率和冷凝側風機頻率對系統總功率的影響情況如圖5所示。

圖5 蒸發器側風機頻率和冷凝側風機頻率對系統總功率的影響情況Fig.5 The influence of evaporator sidewind frequency and condensation sidewinder frequency on the total power of the system

從圖5中可以看出，隨著蒸發器側風機和冷凝側風機頻率的增加，系統總功率呈現出先減小后增加的趨勢，地鐵站的冷側風機為送風機，送風機頻率的增大使得風量增加，降低了壓縮機的功率，導致系統總能耗下降。當蒸發器側風機頻率在20-30Hz 范圍內，冷凝側風機頻率在25-35Hz 范圍時，系統總功率最低。但是冷凝溫度偏高存在制冷劑泄漏的風險，因此選擇蒸發器側風機頻率25Hz，冷凝側風機頻率30Hz 為最佳工況點，此時系統總功率為277.5kW，相較于歷史數據降低了37.3kW，減少了系統總能耗。為了驗證運行優化模型的適用性和有效性，對來自20 個地鐵站歷史數據的35 個典型工況進行運行優化驗證，原始工況和優化工況的對比結果如圖6所示。

圖6 原始工況和優化工況的對比結果Fig.6 Comparison results of the original and optimized conditions

從圖6中可以看出，經過優化調整，優化工況下制冷系統的總能耗相較于原始工況均有所降低，總能耗降幅在8.7%-23.6%范圍內，降幅最大工況為測試工況6，測試工況6 的原始能耗為254kW，而優化后系統總能耗為195kW，降低了59kW，能耗降幅為23.6%。降幅最小工況為測試工況23，工況23 的原始能耗為183kW，優化后能耗降為167kW，降低了16kW，降幅為8.7%。結果證明研究所提出的運行優化模型能有效降低制冷系統的總功率，能適用于不同運行條件下的地鐵空調系統，對降低地鐵站冷凝通風系統的能源消耗具有重要價值。

3 結論

為了提升地鐵冷凝通風制冷空調系統的節能性，研究結合分布參數法和順序模塊法建立空調系統的數學模型，并進行求解，對空調系統的運行參數情況進行深入分析，建立空調系統的節能運行優化模型，提出地鐵冷凝通風制冷空調系統的自適應運行優化模型。實驗結果表明，研究所構建的模型制冷量仿真值與制冷實際量之間的誤差也均未超過10%，符合工程計算標準。模型吸氣溫度仿真誤差均小于1℃，排氣溫度仿真誤差范圍不超過10%，平均仿真誤差值為3.26±1.42℃，滿足模型設計要求。經過優化調整，優化工況下制冷系統的總能耗降幅在8.7%-23.6%范圍內，能有效降低制冷系統的總能源消耗，提升空調系統的環保性和節能性。未來可以在數值模擬的基礎上，引入深度學習技術對歷史數據進行深入挖掘，建立前饋預測系統，實現對地鐵空調系統的預調節。