考慮風電預測誤差時序性及風電可信度的雙層優化模型

徐 詢 謝麗蓉 梁武星 葉家豪 馬 蘭

考慮風電預測誤差時序性及風電可信度的雙層優化模型

徐 詢 謝麗蓉 梁武星 葉家豪 馬 蘭

（可再生能源發電與并網技術教育部工程研究中心（新疆大學） 烏魯木齊 830047）

推動風電等清潔能源是實現雙碳目標的有力舉措。為此針對風電的不確定性，提出考慮風電預測誤差時序性及風電可信度的雙層優化模型。首先，根據風電預測誤差的時序相關性優化預測誤差分段數；然后，建立雙層優化模型，日前階段上層模型基于風電功率上下波動域以最大化利用風電和最小化發電成本及碳交易成本為目標函數，日內階段基于風電概率性場景以最小化系統偏差校正成本及風險成本為目標函數，并考慮激勵型需求響應，通過風電可信度耦合關聯上下層模型；最后，以新疆某地區風電場數據進行仿真分析，結果表明所提模型能夠降低系統風險成本，協調風電和火電的輸出功率，并提高風電接入系統的整體經濟性。

風電預測誤差 概率密度分布 自動發電控制 雙層優化模型

0 引言

2020年9月，我國提出2030年前實現碳達峰，努力爭取2060年前實現碳中和。研究碳中和背景下能源系統的低碳化轉型，將加速風電等其他可再生能源的不斷應用[1]。隨著風電并網容量的增加，風電固有的不確定性使得電力系統運行存在風險[2-3]，不僅增加了電力系統調度的難度，還影響其經濟性。故當前提高風電消納能力及保證電力系統安全性是雙碳目標的一個關鍵任務。

現階段針對風電并網經濟調度問題已有一些研究。總體可分為兩類，分別為確定性方法和不確定性方法。確定性方法即將風電預測功率視為確定值，常規機組預留足夠的備用容量以此改善風電不確定性。不確定性方法則是將風電功率或風電預測誤差等視為調度模型中的不確定性變量，以此確定經濟性最優的機組組合。故而考慮具有風電不確定信息的預測誤差概率分布進行調度成為研究新方向[4-6]。

在風電預測誤差概率分布研究方面，文獻[7]采用TLS（t location-scale）分布描述風電功率預測誤差分布；文獻[8]以風電集群為主體，認為風電集群預測誤差采用非參數核密度估計為最佳擬合模型方法；文獻[9]采用核密度估計方法建立各類樣本在不同風向條件下的風速-風電功率預測誤差聯合概率密度分布模型；文獻[10]利用非參數核密度估計方法計算預測誤差的概率密度分布及光伏日前功率預測值的置信區間。以上文獻利用參數估計或非參數估計進行風電/光伏預測誤差特性分析，但未考慮風電預測誤差隨時間變化的規律性。

在基于預測誤差構建調度模型研究方面主要采用魯棒優化方法[11-13]，文獻[14]在考慮風電預測誤差的最惡劣概率分布條件下，運用基于Wasserstein距離的分布魯棒算法，提出了微電網兩階段分布魯棒優化模型；文獻[15]通過統計學理論，利用-散度構建較高置信水平下的風電功率預測誤差不確定概率的置信域，建立基于條件風險價值的動態經濟調度風險費用魯棒優化模型；文獻[16]根據風電預測誤差建立一種基于0-1規劃的運行風險模型，將其模型與魯棒UC（unit commitment）模型結合并動態地調整風電不確定集合的邊界，實現運行成本和運行風險的協同優化。魯棒優化模型雖能保證可靠性，但對于風電預測誤差大多采用極端分布估計，概率密度函數適應性較差，使得結果趨于保守。基于風電預測誤差分布構建調度模型大多采用隨機優化方法[17-18]，文獻[19]在研究風電預測誤差分布特性后，基于機會約束混合整數規劃建立考慮風電功率特性的風火協調滾動優化調度；文獻[20]提出了基于預測誤差分布的風功率隨機性分析法，將生成的風電出力場景應用于基于頻率響應的優化調度模型中；文獻[21]考慮風電功率預測誤差，從不同階段構建了電力系統需求響應多時間尺度優化調度模型；文獻[22]在風電預測誤差滿足正態分布的條件下生成風電出力場景，提出了一種考慮風電有功降載運行的兩階段系統備用計劃雙層優化模型。

基于以上分析，本文分析風電預測誤差分布的時序特性，并建立風電功率上下波動域描述風電隨機性，構建考慮風電預測誤差時序性及風電可信度的雙層優化模型。其中上層模型以系統發電成本最小為目標函數，將各發電源的計劃出力及風電允許出力域作為決策變量；下層模型引入激勵型需求響應，以自動發電控制（Automatic Generation Control, AGC）機組校正成本及系統成本最小為目標函數，通過風電可信度關聯上下層模型。該雙層模型可用于風電并網后制定機組運行計劃和評估系統經濟性。

1 日前-日內階段雙層優化模型框架的構建

為了應對風電并網對電力系統帶來的一系列挑戰，本文建立了日前-日內階段雙層優化模型。其模型架構如圖1所示。

圖1 日前-日內雙層優化模型框架

如圖1所示，日前運行階段上層模型采用自適應帶寬法的非參數核密度估計風電預測誤差概率分布，并通過相關性分析優化預測誤差的時序分段，由此建立風電功率上下波動域。上層模型以實現風電利用最大化和系統發電成本最小化為目標，求解非AGC機組、AGC機組和風電計劃出力以及風電允許出力域，其中風電計劃出力根據日內階段場景的風電可信度決定，風電允許出力域使得風電場控制具有更大的靈活性，且通過參與因子決定AGC機組的出力決策以應對風電波動。日內優化階段下層模型以實現最小化計劃偏差、懲罰成本以及可中斷負荷成本為目標，在源側考慮到s個可能的日內階段場景得到該階段下的風電可信度并反饋至上層模型中，在負荷側引入激勵型需求響應及考慮負荷誤差生成負荷場景。下層模型通過跟蹤上層模型得出的計劃出力值，從而更新風電允許出力域及調整AGC機組出力。

2 風電預測誤差的不確定性模型

2.1 風電功率預測誤差概率分布

風電場運行中由于風電預測方法、預測模型的精確程度以及地理環境均會導致風電預測誤差，本文選取中國新疆某地區風電場的2020年12月風電功率實際值與預測值進行預測誤差分析。

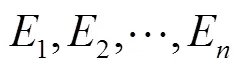
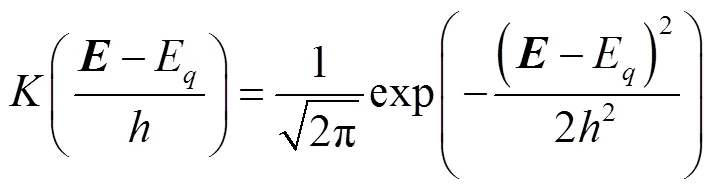
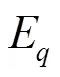
計算最終的概率密度函數之前需先獲得參數，本文采用最大似然估計計算非參數估計模型參數，非參數核密度估計采用自適應帶寬法[23]求取合適的帶寬。

利用dfittool擬合工具箱擬合的非參數核密度估計命名為非參數估計1，利用自適應帶寬法擬合的非參數核密度估計命名為非參數估計2。采用正態分布、TLS分布、非參數估計1及非參數估計2的擬合效果如圖2所示。

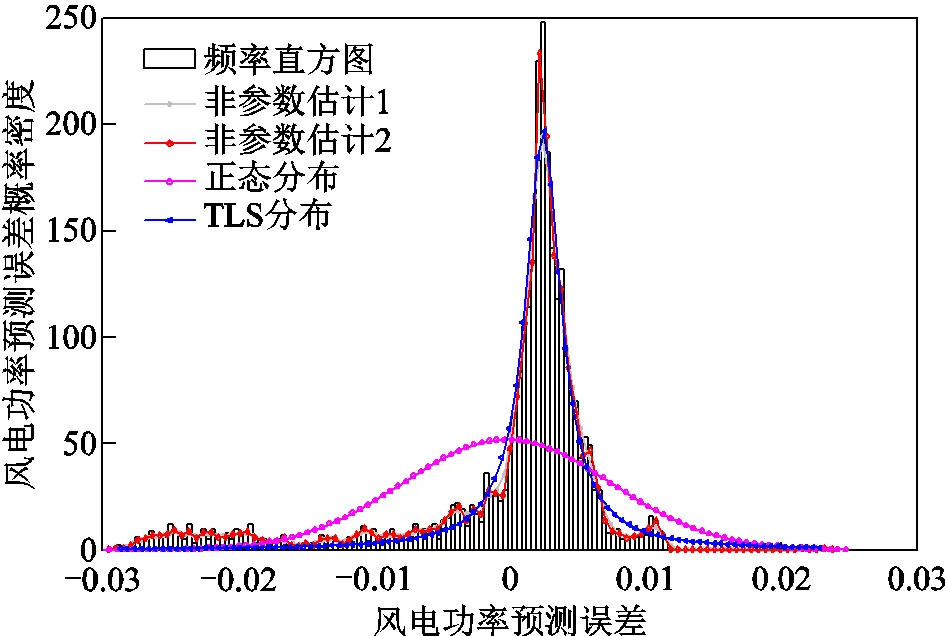
圖2 風電預測誤差的概率密度分布擬合圖

圖2中風電預測誤差的概率分布直方圖呈現中間高兩側低的趨勢，從各分布模型擬合結果可看出，正態分布對于腰部的擬合效果不佳，同時正態分布與TLS分布均不能很好地擬合風電功率預測誤差概率分布尖峰厚尾、非對稱的特征，非參數核密度估計則相反，其模型形狀靈活。為了驗證擬合精度，采用K-S檢驗對以上分布的累積分布函數進行擬合優度檢驗，設定K-S檢驗的顯著性水平為0.05。

正態分布在進行K-S檢驗時值為1，表示拒絕原假設，其余分布的值為0，表示接受原假設。TLS分布、非參數估計1及非參數估計2擬合優度返回的值大于0.05，分別為0.917 3、0.932 2和0.967 6，從值大小可發現，采用自適應帶寬法的非參數估計2擬合精度高于采用擬合工具箱的非參數估計1，體現了自適應帶寬法的適用性。故本文利用自適應帶寬法的非參數核密度估計進行后續的誤差時序性分析。

2.2 時序下的預測誤差擬合方法

風電預測誤差往往隨著預測步長的不同而發生變化，且預測誤差在時序上存在相關性。當進行風電預測誤差的特性分析時，考慮誤差時序上的差異性和相關性才能真實反映風電預測誤差[24]。在確定擬合方法和參數后對數據進行時序分段擬合，24時段預測誤差擬合結果如圖3所示。

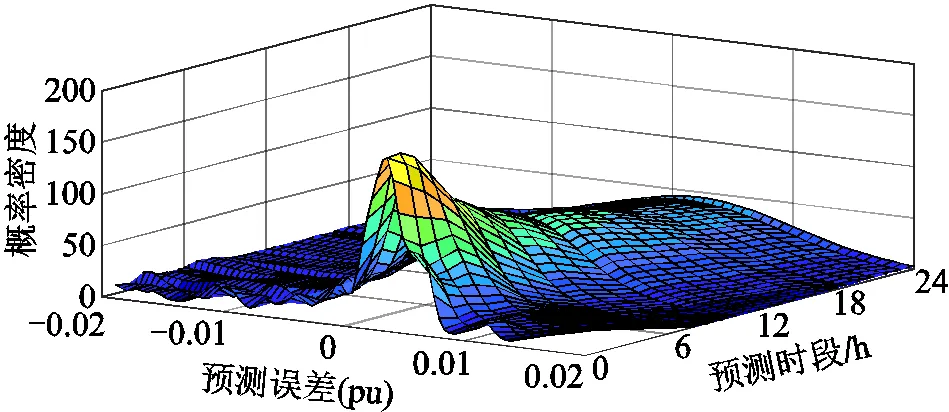
圖3 時序分段預測誤差分布

由圖3可知，隨著預測步長的增加，各時段下的風電預測誤差擬合結果不唯一，顯然不考慮時序性進行研究將影響實驗結果，但若按照時序進行風電預測誤差的分段將會導致計算量增大，此時可依據相關性分析優化時序分段數。各時間段間的相關系數矩陣如圖4所示。

圖4 各時間段間的相關系數矩陣

由圖4可知，每個方塊區域代表各時刻間預測誤差的相關系數，橫縱坐標代表時間。基于相關系數強相關原則可優化時序分段數，即相關系數大于0.8的歸為一組，且不重復已選中的時段，由此重新劃分時序范圍。該步驟考慮了風電預測誤差的相關性，減少了時序分段數，從而降低計算量。優化后的時序分段為[1h,5h]、[6h,7h]、[8h,11h]、[12h,15h]、[16h,21h]、[22h,24h]。最后基于優化后的時序分段建立日前階段的風電功率上下波動域以及生成日內風電出力場景。

3 風電功率上下波動域的建立

在風電功率預測精度的基礎上，當風電概率預測誤差滿足某種概率分布時，利用置信水平表示風電出力落在某一范圍內的概率，可通過風電置信度計算風電功率上下波動域。

參考以上步驟，基于優化后的時序分段并利用風電置信度構建風電功率上下波動域，建立雙層優化模型，可計算得到風電允許出力域，使得系統經濟成本最優。計算某日的兩個風電場置信水平為60%～95%的風電功率上下波動域。采用區間覆蓋率和敏銳性指標[25]求解得到選取90%及95%置信水平下的風電功率上下波動域的區間覆蓋率及敏銳性指標最大，故本文將90%置信度下的波動域考慮到模型中。

4 日前-日內階段雙層優化模型的建立

針對風電不確定性導致系統經濟效益低等問題，提出一種考慮日前風電功率上下波動域及日內風電出力場景改善不確定性的雙層優化模型。日前運行階段上層模型以1h為調度間隔，以規劃周期（24h）內綜合成本最小為目標。日內優化階段下層模型以15min為調度間隔，每隔4h對風電場的預測數據更新一次，根據最新的風電預測信息重新優化日內調度模型并執行下一時刻的調度計劃。下層模型以計劃偏差、懲罰成本及可中斷負荷成本最小為目標，在日內階段下層模型中考慮風電可信度，日前-日內階段的優化問題具有互動性，兩者可統一為雙層優化模型。

4.1 日前運行階段上層模型

上層模型利用風電功率上下波動域考慮風電的不確定性及波動性。該模型的目標函數為實現利用風電最大化和系統計劃發電成本最小化。模型的目標函數為

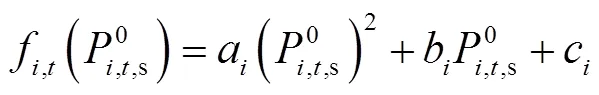
由于風電場的出力波動需要由AGC機組承擔，在上層模型中為了考慮風電出力的不確定性，AGC機組的實際出力為

1）非AGC機組和AGC機組出力約束

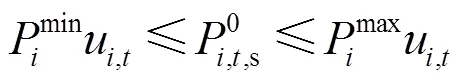
2）非AGC機組和AGC機組爬坡約束

3）風電出力約束

4）旋轉備用約束

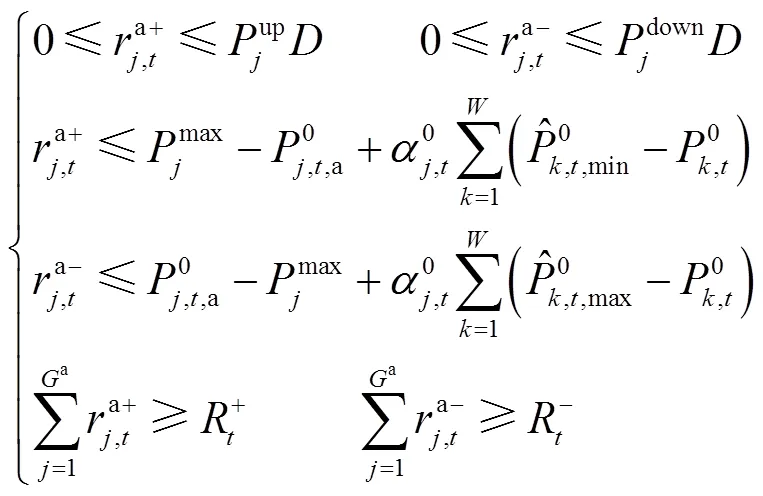
5）AGC機組參與因子約束

6）啟停時間約束

7）線路傳輸容量約束

8）風電功率爬坡約束

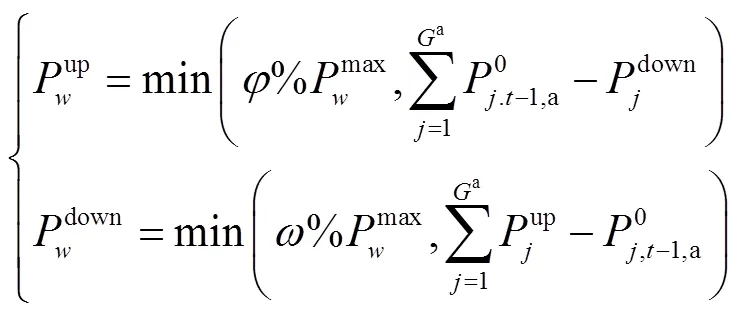
4.2 日內優化階段下層模型

下層模型的目標函數為實現最小化系統計劃偏差校正量以及系統風險成本，考慮到s個可能的風電日內出力場景，并將激勵型需求響應引入到模型中，模型的目標函數為

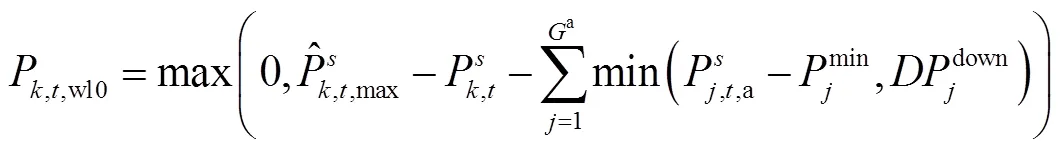
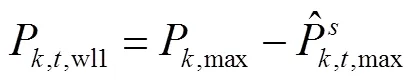
下層模型的約束條件包括功率平衡約束、AGC機組出力約束、風電出力約束和可中斷負荷削減容量約束。

1）功率平衡約束

2）AGC機組出力約束

3）風電出力約束

4）可中斷負荷削減容量約束

4.3 日前-日內階段雙層優化模型

由于本文的雙層優化模型屬于非線性模型，難以直接求解，需將雙層模型轉換為單層模型，考慮通過構建下層模型的拉格朗日函數，基于KKT（Karush-Kuhn-Tucker）條件，并通過引入輔助的0-1變量，將模型轉換為最終的單層線性模型，推導結果如下。

優化目標函數：式（5）。約束條件如下。

（1）原上層約束條件：式（13）～式（26）。

（2）原下層模型利用KKT條件引入的下層等效約束條件如式（37）～式（41）所示。

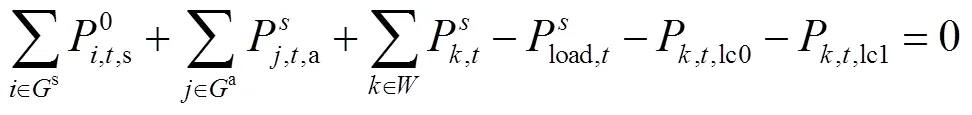
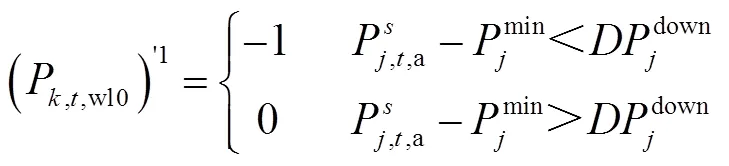
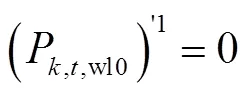
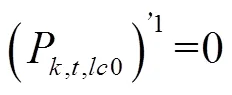
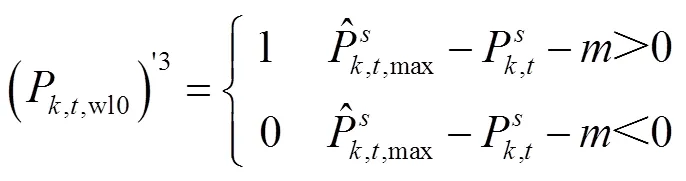
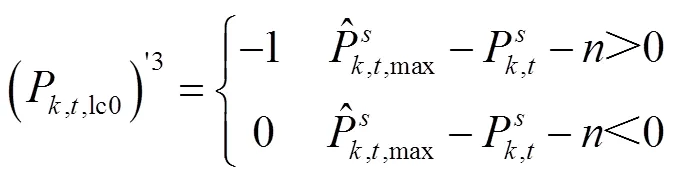
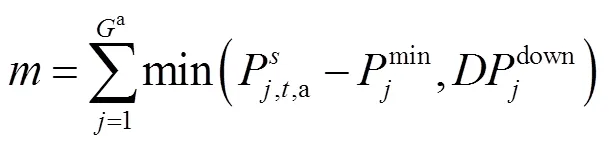
5 算例分析

采用修改的IEEE 30節點系統驗證本文所提優化模型的可行性。利用YALMIP工具箱調用CPLEX12.6求解器在Matlab 2016a平臺上進行求解。使用中國新疆地區某風電場實測和預測數據進行測試。

5.1 不同情景下仿真結果

修改的IEEE 30節點包含6臺火電機組，總裝機容量為477.5MW，將機組G1～G3設為非AGC機組，機組G4～G6設為AGC機組。風電場接入13號與21號節點。設定風電損失懲罰系數為76$，可中斷負荷的單位補償費用為1 493$。負荷曲線如圖5所示，非AGC機組和AGC機組參數見表1。

圖5 負荷及風電場預測功率曲線

表1 發電機組參數

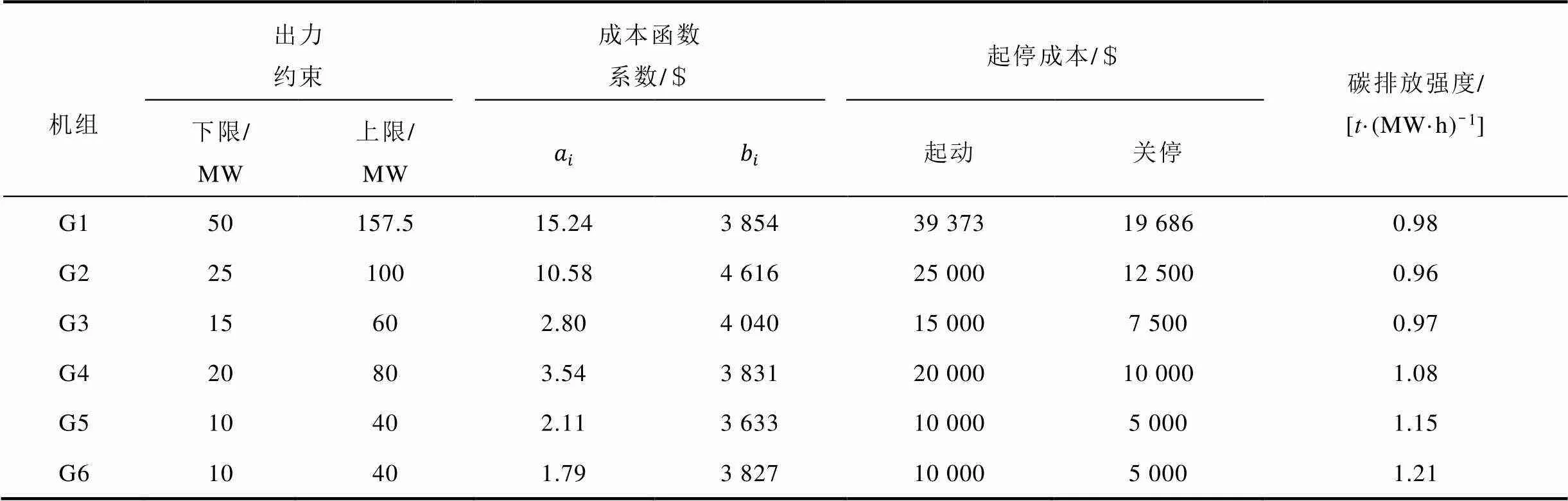
Tab.1 Parameters of conventional generator set

本算例通過五種情景進行對比，均考慮碳交易成本。

情景1：傳統確定性優化模型。將風電預測功率視為確定性參數。

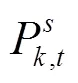
圖6 風電功率場景

圖7 負荷功率場景

情景4：采用本文所提模型，不將火電機組區分為非AGC機組與AGC機組。設置為火電機組的參與因子。

情景5：為研究設置AGC機組對優化結果的影響，設置情景5的AGC機組功率調整平均分配，即參與因子均相等，0.33。

通過優化求解，五種情景下的成本對比見表2。

表2 五種情景的成本對比

Tab.2 Cost comparison of the five scenarios（單位：＄）

由表2可知，情景1在五種情景中的系統綜合運行成本最小，這是由于情景1中未考慮風電的不確定性，系統將存在極大的安全隱患，不利于電網的安全運行。情景2的綜合運行成本高于情景3，由于情景2將花費較多的備用容量成本導致整體成本上升。情景4因未區分AGC機組導致綜合成本高于情景3，雖然情景5和情景3模型相同，但因設定的AGC機組參與因子相同導致綜合運行成本略高于情景3。情景2～情景5的具體優化仿真結果見表3。

表3 情景2～情景5的優化結果

Tab.3 Optimization results from scenario 2 to scenario 5（單位：＄）

由表3可見，情景2的各項成本大多高于情景3～情景5，因情景2的風電預測區間范圍較情景3～情景5的寬，且所求結果偏于保守，導致火電機組和風電為滿足區間范圍內的約束條件使得各項成本上升。因情景4未區分AGC機組，令所有火電機組跟蹤計劃指令值以及預留足夠的備用容量，導致情景4的基本運行成本和碳交易成本明顯高于情景3與情景5。情景5的綜合運行成本略高于情景3，此時情景3的AGC機組參與因子為0.51、0.28、0.21。情景5因設定相同的參與因子導致AGC機組之間的優先級相同，在機組運行時調整功率平均分配，故基本運行成本和碳交易成本較情景3有所增加，使得綜合運行成本高于情景3。情景3對比其他四種情況具有更好的經濟性，在該情景下，通過分類非AGC機組和AGC機組，合理安排AGC機組的出力跟蹤風電不可確定的波動，進一步提高跟蹤風電場景出力曲線的精度，故機組基本運行成本、碳交易成本均較小。

情景3的兩個風電場的功率上下波動域和優化所得的風電功率允許出力區間如圖8所示。由圖8可知，風電場1與風電場2在同一置信水平下，風電場1的波動域范圍寬于風電場2，說明風電場1的不確定性相對較大。01:00～05:00時系統的負荷需求相對較低，而風電場2在此期間出力處于增大趨勢，呈反調峰特性，可能導致AGC機組無法保障全額消納風電場2波動域內的風電功率，故這段期間的系統需要一定的棄風量滿足所有約束條件。06:00～12:00時系統的負荷需求增高，而風電場1與風電場2的出力處于降低趨勢，由于設定的可中斷負荷成本系數較大，需要AGC機組調節功率缺額保證系統的穩定運行，故此期間的基本運行成本增大。情景2與情景3旋轉備用容量對比如圖9所示。

圖8 風電場允許出力域

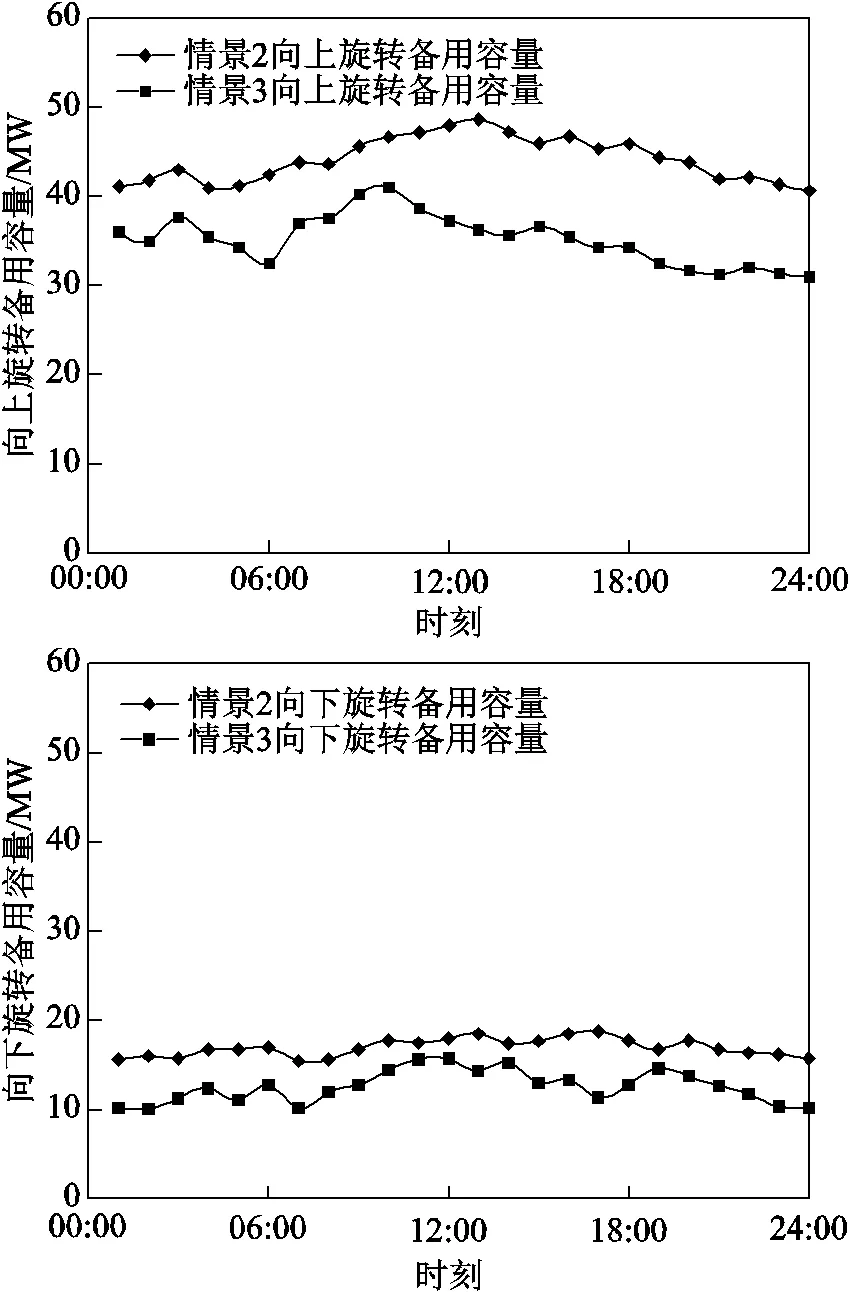
圖9 情景2和情景3的備用容量比較

如圖9所示，由于切負荷現象將對系統造成嚴重的影響，因此設置的切負荷成本系數大于風電損失懲罰系數，導致系統的向上旋轉備用容量大于向下旋轉備用容量。另一方面，情景2得到的機組組合結果偏于保守，情景2的向上和向下旋轉備用容量均大于情景3，反映出表3中情景2的綜合運行成本大于其他情景下綜合運行成本的原因。

5.2 L值的分析結果

為探究風電滲透率與風電可信度的關系，圖10為日前運行階段風電可信度的優化結果，其中時刻風電滲透率定義為

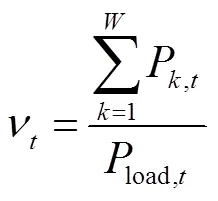
由圖10可知，風電場的值與風電滲透率存在著密切的關系，風電滲透率較高時，因可中斷負荷的成本遠高于棄風損失懲罰成本，此時風電場1和風電場2的值較小，代表風電可信度高；在風電滲透率較低時，為了讓系統保持足夠的可靠性，風電場1和風電場2的值較大，表示此時風電可信度低。

5.3 不同置信水平下仿真結果

置信水平表示系統能接受的風險水平，置信水平值較大時，相應的風電功率上下波動域也就越大，則系統的備用容量隨之增大，此時系統的可靠性雖高但承擔的備用成本也隨之增大。置信水平值較小時則相反。為進一步研究不同置信水平對優化結果的影響，以場景1為例分別求解置信水平為60%、70%、80%、90%、95%、100%時的向上、向下旋轉備用成本及系統運行風險成本，設置向上、向下旋轉單位備用成本為30$/MW，優化結果如圖11所示。

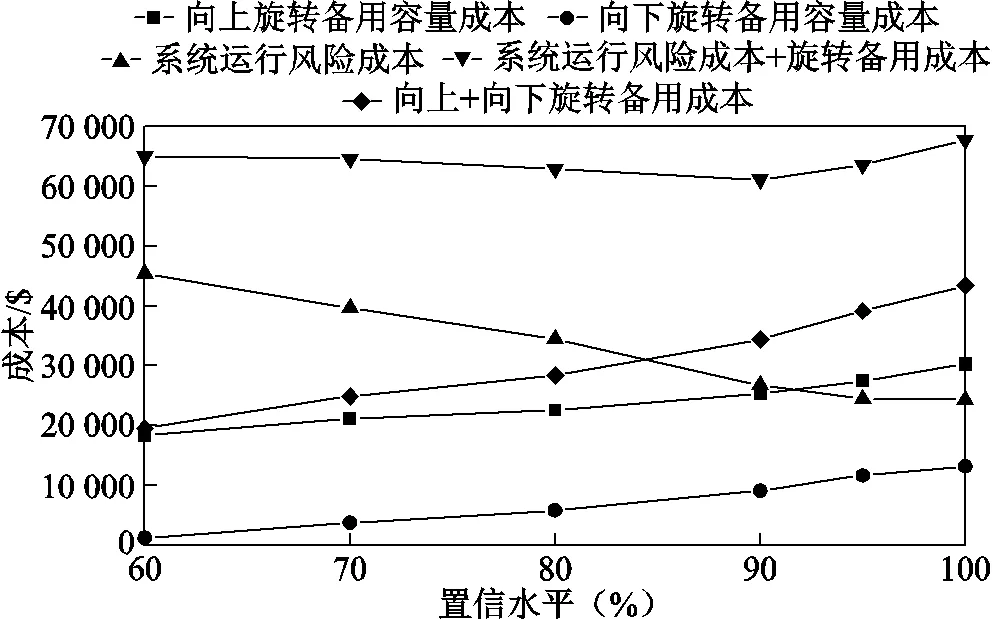
圖11 不同置信水平旋轉備用成本與系統運行風險成本

如圖11所示，系統的向上與向下旋轉備用容量成本隨著置信水平的增加而增加，因此向上與向下旋轉備用成本之和隨之增加。且在優化過程中設置的向上旋轉備用容量大于向下備用容量，故在同一置信水平下前者成本總是高于后者。系統運行風險成本卻隨著置信水平的增大而減小，這是由于置信水平越大，系統發生風電損失和切負荷風險的概率越低，使得系統運行風險成本也隨之減少。旋轉備用成本與系統運行風險成本兩者總成本則隨著置信水平的增大呈先減少再增大的趨勢，可看出置信水平在90%左右總成本相對較小，因此證明置信水平設置為90%左右合適。

6 結論

針對風電并網對電力系統造成的影響，本文建立了含風電的電力系統日前-日內階段雙層優化模型，基于風電預測誤差時序性構建風電功率上下波動域及生成日內風電場景考慮風電的不確定性，通過對模型的求解及算例分析，得到如下結論：

1）對于風電預測誤差的概率密度分布，采用自適應帶寬法的非參數核密度估計擬合精度優于本文對比的其他擬合方法，利用非參數核密度估計進行預測誤差的時序性分析，優化時序分段數，不僅減少了計算量，還進一步提高了擬合精度。

2）提出考慮風電預測誤差時序性及風電可信度的日前-日內雙層優化模型，上層模型以日前系統運行綜合成本最小為目標，求解了AGC機組參與因子與風電允許目標域，下層模型基于日內場景以風電和AGC機組調整出力跟蹤計劃出力令偏差及各項成本最小為目標，使得優化結果更加合理。并且模型考慮的風電可信度可作為調度信號引導風電場合理并網。

3）分析向上和向下旋轉備用成本以及系統運行風險成本隨不同置信水平的變化規律，給出合理的置信區間可兼顧系統運行的經濟性和供電可靠性。

[1] 黃雨涵, 丁濤, 李雨婷, 等. 碳中和背景下能源低碳化技術綜述及對新型電力系統發展的啟示[J]. 中國電機工程學報, 2021, 41(增刊1): 28-51.

Huang Yuhan, Ding Tao, Li Yuting, et al. Decarbonization technologies and inspirations for the development of novel power systems in the context of carbon neutrality[J]. Proceedings of the CSEE, 2021, 41(S1): 28-51.

[2] 葉林, 路朋, 趙永寧, 等. 含風電電力系統有功功率模型預測控制方法綜述[J]. 中國電機工程學報, 2021, 41(18): 6181-6197.

Ye Lin, Lu Peng, Zhao Yongning, et al. Review of model predictive control for power system with large-scale wind power grid-connected[J]. Proceedings of the CSEE, 2021, 41(18): 6181-6197.

[3] 路朋, 葉林, 裴銘, 等. 風電集群有功功率模型預測協調控制策略[J]. 中國電機工程學報, 2021, 41(17): 5887-5899.

Lu Peng, Ye Lin, Pei Ming, et al. Coordinated control strategy for active power of wind power cluster based on model predictive control[J]. Proceedings of the CSEE, 2021, 41(17): 5887-5899.

[4] Khorramdel B, Zare A, Chung C Y, et al. A generic convex model for a chance-constrained look-ahead economic dispatch problem incorporating an efficient wind power distribution modeling[J]. IEEE Transactions on Power Systems, 2020, 35(2): 873-886.

[5] Yan Jing, Ouyang Tinghui. Advanced wind power prediction based on data-driven error correction[J]. Energy Conversion and Management, 2019, 180: 302-311.

[6] 張沛, 田佳鑫, 謝樺. 計及多個風場預測誤差的電力系統風險快速計算方法[J]. 電工技術學報, 2021, 36(9): 1876-1887.

Zhang Pei, Tian Jiaxin, Xie Hua. A fast risk assessment method with consideration of forecasting errors of multiple wind farms[J]. Transactions of China Electrotechnical Society, 2021, 36(9): 1876-1887.

[7] 畢平平, 許曉艷, 梅文明, 等. 風電基地連鎖脫網風險評估方法及送出能力研究[J]. 電網技術, 2019, 43(3): 903-909.

Bi Pingping, Xu Xiaoyan, Mei Wenming, et al. Study on cascaded tripping-off risk assessment method and delivery capacity of wind power base[J]. Power System Technology, 2019, 43(3): 903-909.

[8] 孫亞南, 黃越輝, 孫誼媊, 等. 基于運行數據的短期風電功率預測誤差互補特性探析[J]. 電力系統自動化, 2021, 45(21): 215-223.

Sun Yanan, Huang Yuehui, Sun Yiqian, et al. Operation data based analysis on complementary characteristics of short-term power prediction error for wind power[J]. Automation of Electric Power Systems, 2021, 45(21): 215-223.

[9] 余灃, 董存, 王錚, 等. 考慮山東近海不同風能天氣特征的風電功率區間預測模型[J]. 電網技術, 2020, 44(4): 1238-1246.

Yu Feng, Dong Cun, Wang Zheng, et al. Wind power interval forecasting model considering different wind energy weather characteristics in Shandong offshore areas[J]. Power System Technology, 2020, 44(4): 1238-1246.

[10] Gu Bo, Shen Huiqiang, Lei Xiaohui, et al. Forecasting and uncertainty analysis of day-ahead photovoltaic power using a novel forecasting method[J]. Applied Energy, 2021, 299: 117291.

[11] Yang Jun, Su Changqi. Robust optimization of microgrid based on renewable distributed power generation and load demand uncertainty[J]. Energy, 2021, 223(6): 120043.

[12] 羅毅, 邵周策, 張磊, 等. 考慮風電不確定性和氣網運行約束的魯棒經濟調度和備用配置[J]. 電工技術學報, 2018, 33(11): 2456-2467.

Luo Yi, Shao Zhouce, Zhang Lei, et al. Robust economic dispatch and reserve configuration considering wind uncertainty and gas network constraints[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2456-2467.

[13] 周博, 艾小猛, 方家琨, 等. 計及超分辨率風電出力不確定性的連續時間魯棒機組組合[J]. 電工技術學報, 2021, 36(7): 1456-1467.

Zhou Bo, Ai Xiaomeng, Fang Jiakun, et al. Continuous-time modeling based robust unit commitment considering beyond-the-resolution wind power uncertainty[J]. Transactions of China Electrotechnical Society, 2021, 36(7): 1456-1467.

[14] 朱蘭, 李孝均, 唐隴軍, 等. 考慮相變儲能與建筑蓄能特性的微網分布魯棒優化調度[J]. 電網技術, 2021, 45(6): 2308-2318.

Zhu Lan, Li Xiaojun, Tang Longjun, et al. Distributionally robust optimal operation for microgrid considering phase change storage and building storage[J]. Power System Technology, 2021, 45(6): 2308-2318.

[15] 鄭義, 白曉清, 蘇向陽. 考慮風電不確定性的-散度下基于條件風險價值的魯棒動態經濟調度[J]. 電力自動化設備, 2021, 41(2): 63-70.

Zheng Yi, Bai Xiaoqing, Su Xiangyang. Robust dynamic economic dispatch considering uncertainty of wind power based on conditional value-at-risk under-divergence[J]. Electric Power Automation Equipment, 2021, 41(2): 63-70.

[16] 張智, 陳艷波, 劉芳, 等. 計及運行風險和需求響應的兩階段魯棒機組組合模型[J]. 中國電機工程學報, 2021, 41(3): 961-972.

Zhang Zhi, Chen Yanbo, Liu Fang, et al. Two-stage robust unit commitment model considering operation risk and demand response[J]. Proceedings of the CSEE, 2021, 41(3): 961-972.

[17] 劉文穎, 徐鵬, 趙子蘭, 等. 基于區間估計的風電出力多場景下靜態電壓安全域研究[J]. 電工技術學報, 2015, 30(3): 172-178.

Liu Wenying, Xu Peng, Zhao Zilan, et al. A research of static voltage stability region in wind power scenario based on interval estimation[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 172-178.

[18] 趙冬梅, 殷加玞. 考慮源荷雙側不確定性的模糊隨機機會約束優先目標規劃調度模型[J]. 電工技術學報, 2018, 33(5): 1076-1085.

Zhao Dongmei, Yin Jiafu. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty[J]. Transactions of China Electrotechnical Society, 2018, 33(5): 1076-1085.

[19] 馬燕峰, 陳磊, 李鑫, 等. 基于機會約束混合整數規劃的風火協調滾動調度[J]. 電力系統自動化, 2018, 42(5): 127-132, 175.

Ma Yanfeng, Chen Lei, Li Xin, et al. Rolling dispatch of wind-coal coordinated system based on chance-constrained mixed integer programming[J]. Automation of Electric Power Systems, 2018, 42(5): 127-132, 175.

[20] 徐野馳, 顏云松, 張俊芳, 等. 考慮預測誤差與頻率響應的隨機優化調度[J]. 電網技術, 2020, 44(10): 3663-3670.

Xu Yechi, Yan Yunsong, Zhang Junfang, et al. Stochastic optimal dispatching considering prediction error and frequency response[J]. Power System Technology, 2020, 44(10): 3663-3670.

[21] 李春燕, 陳驍, 張鵬, 等. 計及風電功率預測誤差的需求響應多時間尺度優化調度[J]. 電網技術, 2018, 42(2): 487-494.

Li Chunyan, Chen Xiao, Zhang Peng, et al. Multi-time-scale demand response dispatch considering wind power forecast error[J]. Power System Technology, 2018, 42(2): 487-494.

[22] 楊正清, 汪震, 展肖娜, 等. 考慮風電有功主動控制的兩階段系統備用雙層優化模型[J]. 電力系統自動化, 2016, 40(10): 31-37.

Yang Zhengqing, Wang Zhen, Zhan Xiaona, et al. Bi-level optimization model of two-stage reserve scheduling with proactive wind power control[J]. Automation of Electric Power Systems, 2016, 40(10): 31-37.

[23] Zougab N, Adjabi S, Kokonendji C C. Bayesian estimation of adaptive bandwidth matrices in multivariate kernel density estimation[J]. Computational Statistics & Data Analysis, 2014, 75: 28-38.

[24] 李志偉, 趙書強, 董凌. 考慮預測誤差的風火協調滾動調度[J]. 電力自動化設備, 2020, 40(12): 88-95.

Li Zhiwei, Zhao Shuqiang, Dong Ling. Coordinated rolling dispatch of wind and thermal power considering forecasting error[J]. Electric Power Automation Equipment, 2020, 40(12): 88-95.

[25] 楊茂, 董昊. 基于數值天氣預報風速和蒙特卡洛法的短期風電功率區間預測[J]. 電力系統自動化, 2021, 45(5): 79-85.

Yang Mao, Dong Hao. Short-term wind power interval prediction based on wind speed of numerical weather prediction and Monte Carlo method[J]. Automation of Electric Power Systems, 2021, 45(5): 79-85.

Bi-Level Optimization Model Considering Time Series Characteristic of Wind Power Forecast Error and Wind Power Reliability

Xu Xun Xie Lirong Liang Wuxing Ye Jiahao Ma Lan

（ Engineering Research Center for Renewable Energy Power Generation and Grid Technology Xinjiang University Urumqi 830047 China）

The “dual carbon” goals will promote the continuous application of wind power and other renewable energy. With the large-scale integration of wind power, there would be some risks when the power system operation because of the inherent uncertainty of wind power. While, the traditional deterministic method does not consider the wind power prediction error, and the unit reserves enough reserve capacity to deal with the uncertainty of wind power, so the system has great hidden Security Problems. In recent years, many scholars have constructed robust optimization models based on wind power prediction errors, but the results tend to be conservative. To address these issues, this paper proposes a bi-level optimization model which considering times series characteristic of wind power forecast error and wind power reliability. It effectively improves the economy of power system operation.

Firstly, the adaptive bandwidth method is used to obtain the non-parametric kernel density estimation function of the prediction error, and the time series segment of wind power prediction error is optimized through correlation analysis, and the fluctuation domain of wind power is established according to the time series segment, and the intra-day wind power scenario is generated.

Secondly, the bi-level optimization model is constructed. The upper model in the day-ahead phase the objective function is to maximize the utilization of wind power and minimize the generation cost and carbon transaction cost, to solve the planned output of each unit, wind power and allowable output area of wind power. The planned output of wind power is determined according to the reliability of intra-day wind power scenario. The allowable output area of wind power makes the control of wind power plant more flexible, and determines the output decision of Automatic Generation Control(AGC) units through participation factors to deal with wind power fluctuations. While the lower model in the intraday generates wind power scenarios take the system deviation correction cost and risk cost minimization as the objective function, the source-side considersNpossible scenarios to get the reliability of wind power in stages and feedback to the upper model, the incentive demand response is introduced on the load side, and the lower model updated the allowable output area of wind power and adjusts the output of AGC units by tracking the planned output value obtained from the upper model.

Finally, the proposed model is compared with other models based on the data of a certain region in Xinjiang, and the results are analyzed.

A total of five scenario models are compared. The results show that in scenario 1, the cost is the lowest because the uncertainty of wind power is not considered; in scenario 2, the unit commitment result is conservative lead the cost highest; in scenario 4, the cost is higher than scenario 3 presented because does not distinguish AGC units, and all thermal power units track the command value of the plan and reserve enough spare capacity. In Scenario 5, the set of the same participation factor lead to same priority among AGC units, and distribute power equally to each unit during unit operation, so the cost increases compared with scenario 3.

In order to explore the relationship between penetration of wind power permeability and wind power reliability, the optimization results of wind power reliability in the day-ahead operation stage are analyzed. It can be seen that when wind power permeability is high, wind power reliability is high, and on the contrary, wind power reliability is low. In addition, the spinning reserve cost and system operation risk cost are analyzed with different confidence levels, which prove that the appropriate confidence level is about 90% .

The following conclusions can be drawn from the simulation analysis: (1) the fitting accuracy of the non-parametric kernel density estimation using the adaptive bandwidth method is better than other fitting methods; (2) The economy of the proposed bi-level model is better than other comparison models, and the wind power reliability considered by the model can be used as dispatching signals to guide wind power plantsconnected reasonably; (3) By analyzing the variation rules of spinning reserve cost and risk cost under different confidence levels, a reasonable confidence interval can be given to take into account the economy of system operation and the reliability of power supply.

Wind power forecast error, probability density distribution, automatic power generation control, bi-level optimization model

10.19595/j.cnki.1000-6753.tces.211771

TM614

國家自然科學基金項目（62163034）和新疆維吾爾自治區研究生科研創新項目（XJ2021G060）資助。

2021-11-04

2022-04-15

徐 詢 女，1997年生，碩士研究生，研究方向為風電優化調度。E-mail：839802124@qq.com

謝麗蓉 女，1969年生，教授，博士生導師，研究方向為控制系統優化、新能源發電預測應用。E-mail：xielirong@xju.edu.cn（通信作者）

（編輯 赫 蕾）