物理習題課“立
——破”思維案例分析

米海濱

(烏魯木齊市第四十一中學，新疆 烏魯木齊 830000)

物理習題課是物理眾多課型中至關重要的一種，他直接影響到學生對所學知識的掌握程度，從而影響學生學習物理的興趣，興趣對學生學習物理至關重要，今天和大家交流我自己認為比較有興趣且實用的一種習題課中的“立——破”思維.我的這種思維最早起源于下面這道題.

例1現有一個金和銀組成的王冠，用排水法測出其體積為56.9cm3.若與王冠質量相同的純金塊和純銀塊的體積分別為52.5cm3和96.5cm3，則王冠中銀的質量和金的質量之比為多少？

該題中如果將質量相同的金全部換成銀質量增大44cm3，而本題中最后的合金比純金體積大4.4cm3，所以我們可以將純金和純銀都按質量等分10等份，用一份純銀去替換等質量的一份純金，體積便會增大4.4cm3，也就是說這道題只用一份純銀去替換等質量的一份純金，即合金中有一份純銀，九份純金，質量比為1∶9.對于密度計算，我們會特別關注密度定義質量與體積之比即單位體積的質量.但是上面這道題如果要想到上面的巧解，需要反其道而行之，想到單位質量的體積，上題中等分完每一份純金和純銀的質量都相等，只是體積不同.這道題給了我啟發，讓我研究并實踐了一種提高物理習題課的方法——“立——破”思維，在實際教學中取得很好的效果,所謂“立——破”就是對物理知識先給學生確立一個必須達到的物理達標體系即“立”的過程 ，然后在“立”的基礎上要從不同角度，不同層次對這塊達標體系進行拓展拔高，即“破”的過程，與傳統的拔高的區別在于，這種拔高要有巧勁，要在你的“破”的過程中學生能醍醐灌頂，恍然大悟.這種拔高要有特色，要在你的“破”的過程中學生能感覺到與眾不同，回味無窮.下面就以一些具體例子來淺談“立——破”思維.

1 機械效率習題課的“立——破”思維

例2一花瓶質量約為250kg.為了便于搬運，工作人員先用質量約為50kg的包裝箱對花瓶進行包裝；然后用兩根粗鋼管在高1.2m的車廂與地面之間搭成一個長度約為4.8m的簡易斜面.裝車時，工作人員要用1000N沿平行于鋼管方向的推力把包裝好的花瓶勻速推上車.求：(1)對花瓶做的有用功?(2)搬運花瓶的機械效率?(3)克服摩擦做的額外功?

對于這道題，學生往往對第一問就出問題了，為什么會出現這個問題呢？問題出在“立——破”上.先說說“立”，機械效率中基本的達標線，學生對用斜面拉高物體，有用功等于重力乘以物體移動的高度，總功是人用的力乘以沿這個力方向移動的距離，額外功等于總功與有用功之差.學生在“立”的過程中往往對定義理解不到位，比如用機械拉高物體時對重力的理解，許多同學理解不到位，會將題目背景中的所有重力全部代入，這是有問題的；現在說說“破”，何為有用功，其實就是你使用斜面的目的，這是需要學生理解的，不能死記公式，例如上題中克服包裝紙重力做的功是不是有用功，學生自己要思考這個問題，如果認為是，那就留下花瓶拿走包裝紙，學生肯定不同意，所以包裝紙并不是目的，花瓶才是，包裝紙只是為了保護花瓶是不得不做的功，即額外功.所以對拉高物體的有用功中的重力的理解是需要打破之前的“立”而“破”出新意，于此類似的便是經典的在井中撈水桶問題，如果目的是撈水桶，那克服水桶重力所做的功便是有用功，克服水桶中的水的重力所做的功便是額外功.如果換個情景，目的是用水桶打水，那克服水桶重力所做的功便是額外功，克服水桶中的水的重力所做的功便是有用功.

例3利用動滑輪提升一個重為G的物塊，不計繩重和摩擦，其機械效率為60%.要使此動滑輪的機械效率達到90%，則需要提升重力為G的物塊的個數為幾個？

對于這道題，“立”要求學生必須掌握機械效率是有用功占總功的百分比.但對于這道題我們可以這樣“破”——額外功占總功的百分比，即逆向思維，該題中第一次效率為60%，那逆向思維，額外功占總功的比值為40%，就很容易的發現第一次物重和動滑輪為3:2.同樣第二次效率為90%，那逆向思維，額外功占總功的比值為10%，第二次物重和動滑輪為為9:1，由于該題中是用同一個滑輪組將不同物體提升相同高度，又不計繩重和摩擦，所以額外功全部來自克服動滑輪自重而產生的功，兩次大小是一樣的，所以我們可以將第二次物重和動滑輪為9:1變為18：2.這樣就會發現額外功相同時，第二次提起的物體重力與第一次提起的物體重力之比為18：6，為3：1，直接得到3塊的答案.學生需要打破有用功占總功的百分比，而想到額外功占總功的百分比，“破”出思維火花.對于學習能力強的學生我們需要在已突破的體系下再突破，例如下面這道題.

例4某建筑工地上，起重機的吊臂部分為滑輪組,現用該起重機將質量相同的水泥板吊往高處.若第一次、第二次、第三次分別將一塊、兩塊、三塊水泥板吊往某高處，三次起重機做的額外功分別為3000J、4000J、5000J，機械效率分別為η1、η2、η3，則下列關系式正確的是( ).

A．η1>η2>η3B．2η2>η1+η3

C．2η2=η1+η3D．2η2﹤η1+η3

這道題可以嘗試讓學生在前面已有的突破基礎上，再突破到數學思維巧解這個層面上，如圖1是物體重力和滑輪組機械效率的關系圖像，我們只要在這副圖像的基礎上合理代值，例如提一塊水泥板帶機械效率為50%，有圖像可知，用滑輪組提高物體，所提物體越重，機械效率越大，則提二塊水泥板帶機械效率可以賦值為60%，按照圖像走勢，我們會發現雖然物體越重，機械效率越高，但是由于機械效率不能達到100%，所以隨著物體重力的增加，機械效率的增大的幅度會漸漸減小，即η3-η2<η2-η1，所以提三塊水泥板帶機械效率賦值必須小于70%，可以賦值為65%，將三個機械效率建立聯系可以輕松得到答案B.我們要根據自己學生的實際情況去判斷孩是止步于“立”，還是可以“破一”或者是“破二”，需要找到最適合自己學生的習題課方案，適合的才是最美的，才可以培養和保護學生的學習興趣.

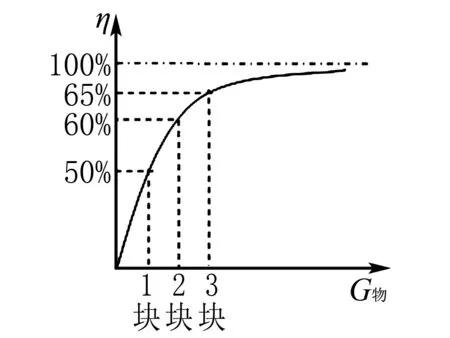
圖1

2 壓強習題課的“立——破”思維

例5一質量為2 kg、厚度均勻的圓柱形容器，放在水平桌面上，與桌面的接觸面積為0.01m2.現往容器內注入0.2 m深的酒精，此時桌面受到的壓強為3.2×103Pa (ρ酒精=0.8×103kg/ m3).求：(1)桌面受到的壓力；(2)酒精對容器底部的壓強；(3)酒精對容器底部的壓力.

對于壓強計算，先說說“立”，學生必須掌握固體壓強一般F=G，P=F/S.液體壓強一般P=ρgh,F=PS.如何“破”，學生對這幾個公式要正確理解，它們其實沒有必須用于固體或液體，四個式子中P=F/S和F=PS是壓強的通用計算公式，固液體都可以用，沒有條件限制，而公式F=G是可以用在液體中的，公式P=ρgh也可以用到固體中，只不過有適用條件--規則柱狀均勻物體.上題中如果學生不能打破這層壁壘，只是按部就班的代公式，由于容器厚度內外面積的不同，最終造成錯誤，這道題固體最終用了F=PS，而液體卻用了F=G.所以我們必須幫助打破對于壓強計算公式的思維定式，我們要給學生打破壁壘，幫助學生靈活運用公式.

例6一密度為ρ的鋼制軸承，由粗細不同的兩部分圓柱體構成，粗細圓柱體的高度均為h.如圖2甲所示放置時，軸承對水平面的壓強為1.2ρgh,如圖2乙所示放置時，軸承對水平面的壓強為多少.

圖2

這道題目中對桌面的壓強，兩種放法物體整體都不是規則柱狀均勻固體，原則上是不能用P=ρgh求固體壓強.適用條件不滿足，如何創造條件運用P=ρgh求固體壓強，如果我們通過擠壓上面的物體的方法可以將物體變為規則柱狀均勻固體，也可以通過擠壓下面的物體的方法可以將物體變為規則柱狀均勻固體，兩種擠壓方法都可以將上下不是柱狀的固體變為上下柱狀的固體，那應該采用哪種方法呢？我們回到壓強的通用公式P=F/S，不管如何擠壓也不能和這個通用公式相矛盾，也就是說你要保證所求的壓強處的接觸面積和壓力在擠壓過程中不能出現變化，按照這個想法，我們會發現上面兩種擠壓方法都不會改變壓力，但是通過擠壓下面的物體的方法可以將物體變為規則柱狀均勻固體的方法會改變物體與桌面的接觸面積，而通過擠壓上面的物體的方法可以將物體變為規則柱狀均勻固體不會改變物體與桌面的接觸面積.所以應該擠壓上面，擠壓之后就可以運用公式P=ρgh，由于物體密度為定值，而P=1.2ρgh，所以擠壓之后總高度為1.2h，下面粗的圓柱體高為h，所以高度為h的細的圓柱體由細變粗后高度變為0.2h,在體積不變的前提下，細圓柱體高度減小了5倍，底面積應該擴大5倍，便可以快速找到粗的底面積是細的底面積的5倍，對于圖2乙，同樣在保證與桌面的接觸面積不變的前提下，也可以通過擠壓上面的物體的方法可以將物體變為規則柱狀均勻固體，即把上面的粗圓柱體擠壓成與下面細圓柱體一樣粗的圓柱體，粗圓柱體底面積縮小5倍，高度就應該增加5倍，變為5h，在加上下面細圓柱體的高度h，總共6h,從而運用公式P=ρgh，快速得到如圖2乙所示放置時，軸承對水平面的壓強為6ρgh，運用這種擠壓變形最重要是要保證所求壓強處的接觸面積要保持不變，利用擠壓將不是規則柱狀均勻的固體變為規則柱狀均勻固體，從而利用P=ρgh快速解出題目，獲得成就感，我們老師要根據自己、學生、學校的實際情況，是讓學習有困難的學生掌握固體壓強一般F=G，P=F/S.液體壓強一般P=ρgh,F=PS.一般學生要突破到公式的靈活運用，再有能力的孩子讓他創造條件用公式.讓不同層次的孩子都有所獲，有所感，收獲成功和喜悅.習題課中的“立——破”思維則是在習題課中的分層教學，教師課前的工作會更多，即要合適高效的分層，更要針對自己的學生有特色的設計習題課.

我們要研究習題課的設計，這是對學生學習物理的負責，也是對學生未來的負責.我們要通過習題課鞏固加強學生學習物理的興趣，不能讓習題課只是機械加強鞏固學生的基礎知識與基礎技能，而應該是定位準確，合理立破，層層遞進，讓不同層次的學生都有收獲，都有發展，都能收獲幸福感，從而提高學生學習物理的興趣.這樣一來，習題課會變成學生學得開心，老師教得順心的歡樂海洋.