數(shù)形結(jié)合思想在初中數(shù)學(xué)解題中的應(yīng)用

林明霞

(福建省莆田市秀嶼區(qū)實(shí)驗(yàn)中學(xué)，福建 莆田 351100)

1 數(shù)形結(jié)合思想的內(nèi)涵

“數(shù)”與“形”是初中數(shù)學(xué)教學(xué)過(guò)程中最為基本的兩個(gè)概念.數(shù)形結(jié)合的思維運(yùn)用其關(guān)鍵就是通過(guò)數(shù)量和圖形相互結(jié)合，促進(jìn)學(xué)生對(duì)數(shù)學(xué)解題有更加深刻的解題思維.數(shù)形結(jié)合需要將數(shù)學(xué)定理、公式與圖形相結(jié)合，并引導(dǎo)學(xué)生對(duì)數(shù)學(xué)問(wèn)題進(jìn)行思考.在日常的教學(xué)過(guò)程中，普遍使用的教學(xué)形式主要表現(xiàn)在用數(shù)來(lái)研究圖形與用圖形來(lái)研究數(shù)，根據(jù)教學(xué)形式的不同分為了“以形助數(shù)”與“以數(shù)解形”兩個(gè)方面.在初中數(shù)學(xué)中，數(shù)量問(wèn)題主要分為代數(shù)問(wèn)題、函數(shù)問(wèn)題、集合問(wèn)題等.在初中數(shù)學(xué)的解題步驟中要運(yùn)用好數(shù)形結(jié)合的思想,將抽象的數(shù)量問(wèn)題轉(zhuǎn)化為具體的圖形問(wèn)題,或者將直觀的圖形轉(zhuǎn)化為準(zhǔn)確的數(shù)量.

2 數(shù)形結(jié)合思想在初中數(shù)學(xué)解題中的意義

2.1 培養(yǎng)學(xué)生的解題興趣

初中數(shù)學(xué)題目涉及邏輯和思維，難度大，初中學(xué)生在數(shù)學(xué)解題過(guò)程中感到枯燥乏味，容易導(dǎo)致學(xué)生失去學(xué)習(xí)的信心.在日常教學(xué)過(guò)程中，教師要充分調(diào)動(dòng)學(xué)生對(duì)數(shù)學(xué)這一課程的學(xué)習(xí)欲望，教師要對(duì)自身的教學(xué)觀念進(jìn)行不斷更新.比如教師在教學(xué)過(guò)程中引入圖像的表現(xiàn)方式，將二次函數(shù)以形象化的方式表現(xiàn)出來(lái).同時(shí)可以結(jié)合互聯(lián)網(wǎng)PPT對(duì)教學(xué)圖像進(jìn)行展示，從而達(dá)到吸引學(xué)生學(xué)習(xí)二次函數(shù)的欲望，激發(fā)學(xué)生對(duì)數(shù)學(xué)的學(xué)習(xí)熱情，也實(shí)現(xiàn)了使學(xué)生在學(xué)習(xí)數(shù)學(xué)的解題思路中快樂(lè)學(xué)習(xí)的教學(xué)初衷.

2.2 發(fā)展學(xué)生的解題思維

初中數(shù)學(xué)的難度隨著知識(shí)的深入不斷加大，很多學(xué)生在解題過(guò)程中出現(xiàn)困難.數(shù)學(xué)解題過(guò)程中需要大量的思維能力，通過(guò)對(duì)數(shù)學(xué)問(wèn)題的本質(zhì)的剖析，數(shù)量關(guān)系與圖形能夠相互轉(zhuǎn)化和補(bǔ)充，讓學(xué)生能夠快速把握問(wèn)題的關(guān)鍵，并對(duì)題意有了更加深刻的印象，解題的思路也變得更加清晰，從而提高學(xué)生在數(shù)學(xué)問(wèn)題中的審題與解題能力，拓寬了學(xué)生思維的發(fā)展.例如，在教授運(yùn)用幾何方法解決代數(shù)問(wèn)題的課程時(shí)，教師可以通過(guò)代數(shù)與幾何圖形的關(guān)聯(lián)度，剖析二者共同點(diǎn)，尋找到科學(xué)的解決方案，提高學(xué)生的邏輯思維能力.

2.3 提升學(xué)生的解題能力

數(shù)形巧妙結(jié)合的思想含義是通過(guò)兩個(gè)數(shù)形概念之間存在的關(guān)系進(jìn)行深入分析，同時(shí)對(duì)幾何空間、數(shù)量關(guān)系等進(jìn)行一個(gè)巧妙的結(jié)合,從而逐步找到一些解題方面的頭緒,讓許多問(wèn)題可以從復(fù)雜變得更加清楚簡(jiǎn)單,最終得到解決問(wèn)題的方案.初中數(shù)學(xué)教學(xué)中比較常見(jiàn)到的幾何代數(shù)問(wèn)題，就可以借助直角三角形、矩形、橢圓等解決.例如,可以考慮借助直角三角形來(lái)解決所有與勾股定理緊密相關(guān)的代數(shù)問(wèn)題.

3 數(shù)形結(jié)合思想在初中數(shù)學(xué)解題中的應(yīng)用

初中數(shù)學(xué)知識(shí)的基本概念有著抽象性的特點(diǎn)，導(dǎo)致學(xué)生對(duì)基本概念的理解容易產(chǎn)生偏差，影響了學(xué)生數(shù)學(xué)解題能力.比如:求得出任何一個(gè)二元一次方程和其中任意一個(gè)一元一次二方程間的正交點(diǎn)的坐標(biāo).在教學(xué)過(guò)程中,要讓學(xué)生自己先以畫(huà)圖的解題思維方式，在一個(gè)坐標(biāo)系圖中畫(huà)出表示兩個(gè)方程式交點(diǎn)的一個(gè)函數(shù)圖像,并能夠在這個(gè)函數(shù)圖中找到這兩個(gè)方程式交點(diǎn)坐標(biāo).而在“以形助數(shù)”的教學(xué)過(guò)程中，要通過(guò)圖像將抽象的數(shù)學(xué)概念正確地表達(dá)出來(lái)，圖像還要表現(xiàn)出數(shù)字與數(shù)字之間的異同關(guān)系.例如，學(xué)生在解一元二次不等式時(shí)，可以直接將代數(shù)代入進(jìn)行運(yùn)算，但存在解題時(shí)間長(zhǎng)、解題思路混亂的問(wèn)題.通過(guò)圖形可以充分解決一元二次不等式的這些問(wèn)題，將不等式兩邊分別看做是一元一次方程和一元二次方程，并把兩個(gè)方程的以圖像的方式在坐標(biāo)系中畫(huà)出，同時(shí)根據(jù)不等式的方向，選擇與方程有交集的圖像，而不等式的解集便是被截取的那一部分.綜上所述，數(shù)形結(jié)合的解題方式對(duì)學(xué)生了解初中數(shù)學(xué)解題思路有著極大幫助.

3.1 數(shù)形結(jié)合解決概念問(wèn)題

初中數(shù)學(xué)概念的課程教學(xué)設(shè)計(jì)目標(biāo)，不僅強(qiáng)調(diào)要讓廣大學(xué)生了解數(shù)學(xué)的基本概念,還要對(duì)其含義形成初步的正確理解.教師們必須反復(fù)對(duì)數(shù)學(xué)的教學(xué)理論進(jìn)行分析，通過(guò)比對(duì)、總結(jié)和歸納概括三個(gè)環(huán)節(jié),對(duì)數(shù)形結(jié)合相關(guān)概念論證的完整邏輯過(guò)程進(jìn)行了詳細(xì)的解析,讓所有學(xué)生從中感知了解每個(gè)數(shù)學(xué)概念背后蘊(yùn)含的數(shù)學(xué)思想.

3.2 數(shù)形結(jié)合解決函數(shù)問(wèn)題

在初中數(shù)學(xué)課程設(shè)計(jì)中，往往會(huì)遇到學(xué)生對(duì)典型的函數(shù)問(wèn)題或復(fù)雜型函數(shù)問(wèn)題的主要概念性質(zhì)關(guān)系無(wú)法正確理解.函數(shù)問(wèn)題研究其實(shí)是一個(gè)包含各種簡(jiǎn)單代數(shù)知識(shí)內(nèi)容與微分幾何知識(shí)內(nèi)容的有機(jī)數(shù)學(xué)綜合體.教師在數(shù)形結(jié)合的教學(xué)基本思想中可以使用“以形助數(shù)”的教學(xué)思維方式.例如,小東正在擊打羽毛球,其中小東的實(shí)際身高約為1.25m，且只能以直線高度BC來(lái)予以表示,而此時(shí)當(dāng)他進(jìn)行擊打后，打飛出來(lái)后的羽毛球的實(shí)際最高直線飛行點(diǎn)的直線高度則恰為2.25 m,此時(shí)若羽毛球與小東的實(shí)際水平距離正好約為1 m,那么羽毛球?qū)嶋H的直線最終的拍落點(diǎn)A和小東的實(shí)際垂直距離應(yīng)是約有多少米長(zhǎng)?這個(gè)數(shù)學(xué)問(wèn)題同樣也有涉及到了關(guān)于“拋物線”知識(shí)中的“應(yīng)用型函數(shù)”的一個(gè)知識(shí)點(diǎn).通過(guò)圖1我們可以很清楚準(zhǔn)確地看到,題目主干信息是所要求函數(shù)的所求B點(diǎn)到函數(shù)所求的A點(diǎn)之間的一條直線距離,通過(guò)這個(gè)圖，學(xué)生們可以對(duì)該函數(shù)題干信息整體有了一個(gè)更加清晰和直觀地了解.

圖1

3.3 數(shù)形結(jié)合解決不等式問(wèn)題

“不等式”是初中數(shù)學(xué)教學(xué)過(guò)程中重要的的一個(gè)知識(shí)點(diǎn)，在解一元一次不等式的過(guò)程中要注意兩點(diǎn)：第一是未知數(shù)前面的系數(shù)是負(fù)數(shù)時(shí)，當(dāng)系數(shù)化1 后，不等式的不等號(hào)要變方向，“>”要變?yōu)椤?”；第二是“≤、≥”表示實(shí)心，“>、<”表示空心.

如圖2，在求不等式的解集時(shí)，為了清楚地得到不等式在數(shù)軸上的解集，重點(diǎn)在于x<1是空心，x≥-2的方向, 因而選擇B.

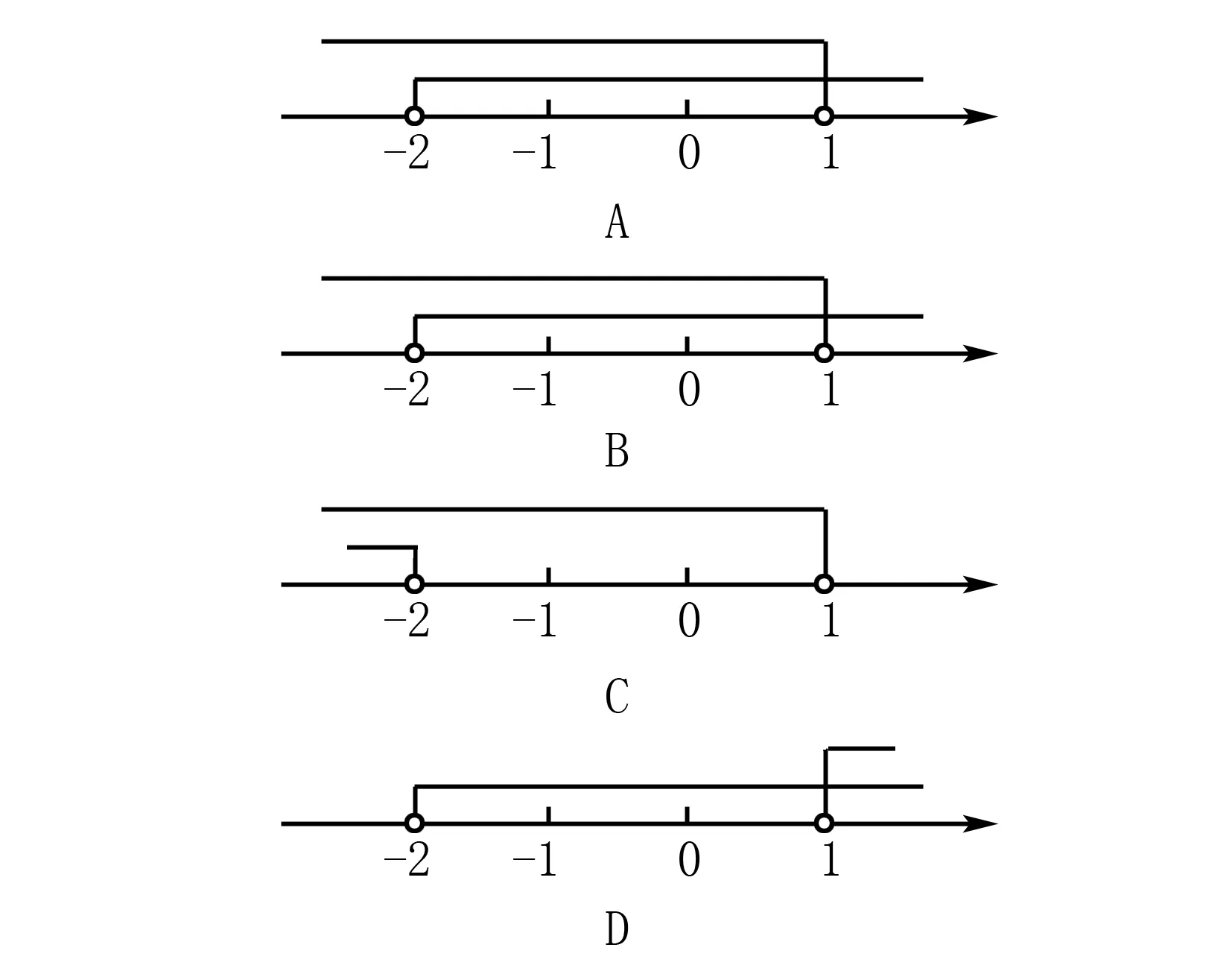
圖2

利用數(shù)軸也可以解決找眾數(shù)和中位數(shù)的問(wèn)題，眾數(shù)是指所有變量中出現(xiàn)次數(shù)最多的數(shù)值，中位數(shù)是將各個(gè)變量按大小的順序排列后，處于中間的變量值.

3.4 數(shù)形結(jié)合解決幾何問(wèn)題

幾何問(wèn)題是初中數(shù)學(xué)的重要部分之一,是每年中考數(shù)學(xué)重點(diǎn)考查的問(wèn)題.通過(guò)幾何問(wèn)題,不僅可以考查學(xué)生對(duì)數(shù)學(xué)知識(shí)的實(shí)際掌握情況及應(yīng)用情況,還能考查學(xué)生的綜合能力及數(shù)學(xué)思維.在圖3中,已知正方形和另一直角三角形邊長(zhǎng)的三邊長(zhǎng)應(yīng)各應(yīng)分別設(shè)為3cm、4cm、5cm.若是要我們分別都是以上所述三條邊中各一條為直徑來(lái)分別去計(jì)算這樣一幅的半圓形,那么該形圖形中的陰影部分的投影總陰影面積是多少平方厘米呢?

圖3

通過(guò)對(duì)題干的分析可以看到，該題目的圖形由三個(gè)直徑分別是5cm、4cm和3cm的半圓和一個(gè)三條邊長(zhǎng)為5cm、4cm和3cm的直角三角形組成，要計(jì)算出陰影面積，就要計(jì)算出直徑為3cm和4cm的兩個(gè)半圓總面積，再減去它們各自的弧形面積.怎樣計(jì)算這兩個(gè)弧形面積的總和呢？是用直徑為5cm的半圓面積減去直角三角形面積得出的.所以要想正確解答這道題，首先要計(jì)算出直徑為5cm的半圓面積，然后減去直角三角形的面積，從而得到兩個(gè)弧形面積的總數(shù).隨后將計(jì)算出直徑為3cm與直徑為4cm的半圓面積進(jìn)行相加，然后減去兩個(gè)弧形的總面積即可得到圖中陰影部分的面積.通過(guò)這個(gè)例子，可以發(fā)現(xiàn)在幾何問(wèn)題的解答思路中數(shù)形結(jié)合思維邏輯的重要性，能夠讓學(xué)生快速審題，并得出問(wèn)題的正確答案.

綜上所述，數(shù)學(xué)結(jié)合思想對(duì)于初中數(shù)學(xué)學(xué)習(xí)與解題具有重要作用.數(shù)形結(jié)合思維邏輯可以讓學(xué)生對(duì)數(shù)字與圖形之間的關(guān)系產(chǎn)生更加深刻的理解，降低解題難度.教師要教會(huì)學(xué)生在數(shù)學(xué)解題的過(guò)程中將數(shù)形結(jié)合的思維邏輯運(yùn)用起來(lái)，實(shí)現(xiàn)提高數(shù)學(xué)成績(jī)的目標(biāo).