引導學生在感悟中學習數學

耿 征

(徐州市第十三中學，江蘇 徐州 221000)

1 發現問題

例1 已知xm=2，xn=5，求xm+n的值.

學生做法：因為xm=2，xn=5

所以xm+n=xm+xn=2+5=7

正確做法：因為xm=2，xn=5

所以xm+n=xm·xn=2×5=10

2 提出問題

為什么學生知道本題是逆用同底數冪的乘法法則，但逆用的過程卻出錯呢？

3 分析問題

冪的四種運算：

(1)積的乘方 (ab)n=anbn

(2)冪的乘方(am)n=amn

(3)同底數冪的乘法am·an=am+n

(4)同底數冪的除法am÷an=am-n

冪的運算法則的應用，主要關注的就是指數之間的進行運算.

冪的四種運算法則的逆用：

(1)積的乘方anbn= (ab)n

(2)冪的乘方amn=(am)n

(3)同底數冪的乘法am+n=am·an

(4)同底數冪的除法am-n=am÷an

冪的運算法則的逆用過程，只有冪之間的乘除關系，沒有加減關系.

學生之所以出現錯誤，原因就在于對冪的運算法則的理解缺少感悟——沒有明確冪運算法則的逆用只有乘除關系，沒有加減關系，如果學生理解這一點，錯誤就不會發生了.

《義務教育數學課程標準》指出：數感主要是指關于數與數量、數量關系、運算結果估計等方面的感悟；關于“零指數”教學方案的設計可作如下考慮：教學目標不僅要包括了解零指數冪的規定，會進行簡單計算，還要包括感受這個規定的合理性，并在這個過程中學會數學思考、感悟理性精神；學生在積極參與教學活動的過程中，通過獨立思考、合作交流，逐步感悟數學思想.

教師的引導作用主要體現在：通過恰當的問題，或者準確、清晰、富有啟發性的講授，引導學生積極思考、求知求真，激發學生的好奇心.

由此可見，在數學教學過程中，我們不能輕易放過出現的問題，不能輕易放過學生提出的疑問，而是要帶領學生及時對出現的問題、產生的疑問反思，找出問題的根源、疑問的解決方法，這就是對數學的感悟.

4 解決問題

4.1 增強對數學定義的感悟能力——看破本質

例2 分解因式6a(1-b)2-2(b-1)2

學生做法：6a(1-b)2-2(b-1)2=(1-b)2(6a-2)

教師引導過程：

教師：這位同學的做法錯在哪里？

學生：(6a-2)沒有分解完.

教師：那應如何繼續分解？

學生：(6a-2)=3 (3a-1)

教師：為什么會出現這種錯誤呢？

學生：應該一開始就提取公因式

教師：所以正確的做法應該為？

學生展示：6a(1-b)2-2(b-1)2=6a(b-1)2-2(b-1)2=2(b-1)2(3a-1)

教師：正確!請大家繼續思考，如何避免類似錯誤再次發生？

學生：……

教師：因式分解的結果要求分解到不能再分解為止，所以建議大家每次因式分解結束，請一定要檢查，是否分解到位！尤其是公因式是否提取完整！

學生沒有分解到位，而這也是學生最容易犯的錯誤.學生之所以沒有分解到位，表面上是因為公因式提取不完整、不全面，而深層次的原因是對因式分解概念本質理解的不清晰.

因式分解是指將一個多項式寫成整式乘積的形式，而因式分解的結果有三個要求：

(1)結果必須是乘積形式；

(2)結果每一項必須是整式；

(3)結果每一項必須分解到不能再分解為止.

這三個要求就是對因式分解本質的解讀.上述案例出錯的原因是沒有達到因式分解的結果的第三個要求.

因此在教學過程中，引導學生每次分解結束，要檢查結果是否分解到位；先考慮提取公因式，而公因式先要考慮系數.

4.2 增強對數學定理的感悟能力——逆向思維

例3如圖1，直線AB、CD被直線EF所截，∠1=75°，下列說法正確的是( ).

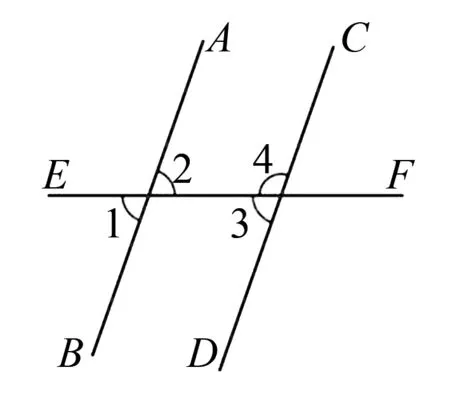
圖1

A.若∠4=75°，則AB∥CD

B.若∠4=105°，則AB∥CD

C.若∠2=75°，則AB∥CD

D.若∠2=155°，則AB∥CD

學生思路1：先看A選項，因為∠4=75°，所以∠3=105°，但∠3≠∠1，所以AB不平行于CD.依次類推，選擇B

學生思路2：由AB∥CD，∠1=75°，可以得到∠2=∠3=75°，∠4=105°，從而確定B正確.

兩種思維過程都是正確的，思路1是多數學生會想到的，是學生做題一般的思維過程.但為什么思路2也可以得到正確答案呢？因為“兩直線平行，同位角相等”與“同位角相等，兩直線平行”是一對互逆真命題，故可以逆向思考.

初中幾何結論中，還有很多互逆真命題，像勾股定理及其逆定理，直角三角形兩銳角互余與兩角互余的三角形是直角三角形等等，教師要及時引導學生建立互逆命題之間的聯系.

在具體解決數學題時，也可以引導學生進行逆向思考.

例4如圖2，在ABCD中點O是邊BC的中點，連接DO并延長，交AB延長線于點E，連接BD，EC．

(1)求證：四邊形BECD是平行四邊形；

(2)若∠A=50°，則當∠BOD為多少時，四邊形BECD是矩形．

圖2

在解決第(2)個問題時，可以考慮先假設四邊形BECD是矩形，逆向推出∠BOD的度數.

4.3 提高對數學圖形的感悟——比較還原

例5已知，∠AOB=90°，點C在射線OA上，CD∥OE．

(1)如圖3，若∠OCD=120°，求∠BOE的度數；

(2)把“∠AOB=90°”改為“∠AOB=120°”，射線OE沿射線OB平移，得O′E，其他條件不變，(如圖4所示)，探究∠OCD、∠BO′E的數量關系；

(3)在(2)的條件下，如圖5，作PO′⊥OB垂足為O′，與∠OCD的平分線CP交于點P，若∠BO′E=α，請用含α的式子表示∠CPO′(請直接寫出答案)．

圖3 圖4 圖5

學生思路：

(1) 因為CD∥OE，所以∠EOC=∠OCD=120°,所以∠BOE=360°-∠EOC-∠COB=150°

圖6

(2)如圖6，過O作OF∥CD，那么OF∥OE′，

所以∠COF=180°-∠OCD，∠FOB=∠OO′E

所以∠COF+∠FOB=180°-∠OCD+∠OO′E=∠AOB=120°,即∠OCD-∠OO′E=60°.

又因為∠OO′E=180°-∠BO′E,

所以∠OCD+∠BO′E=240°.

可以看出，學生把前兩個圖形孤立來看，兩幅圖兩個思考過程.這無形增加了思維量，也降低了解題效率.

引導過程：

教師：請同學們仔細觀察，圖4與圖3比較，哪里發生了變化？

學生：射線OE的位置，∠AOB的大小.

教師：通過你們的做法，可以看出∠AOB的大小，不影響思考過程.那么射線OE位置的改變，導致你們思維過程的變化.那能否還原O′E的位置到OE′)呢？

學生：平移不改變圖形的大小、形狀.也就不改變∠BOE的大小.(這就是感悟的過程)

教師：說的很好，這就是關鍵！當還原OE后，是否借助第(1)問的思維過程進行書寫？

學生：可以發現，∠E′OC=∠OCD,

那么∠EO′B=∠E′OB=360°-120°-∠OCD=240°-∠OCD

教師：很明顯，既簡化了思維過程，也簡化了書寫過程.

教師：請同學們繼續思考，前兩問產生了聯系，那么第(3)問呢？

學生：可以將結論∠OCD、∠BO′E的數量關系直接應用到.

利用四邊形COO′P內角和為360°，就可以用含α的式子表示∠CPO′.

教師：講解正確.確實將發現的結論可以直接利用來解題.

總之，在數學教學過程中，既要時時刻刻關注學生出現的問題，又要時時刻刻對自己的教學進行反思，在感悟中提升，在感悟中進步.