設計參數(shù)變化對懸灌法施工連續(xù)梁橋墩穩(wěn)定性的影響分析

摘要：文章以某懸灌法施工連續(xù)梁橋超高墩穩(wěn)定性為研究對象，通過采用Midas Civil有限元軟件建立橋墩數(shù)值模型，針對不同工況下橋墩結構的穩(wěn)定性展開了分析，并對結構穩(wěn)定性參數(shù)的影響規(guī)律進行了研究。結果表明：一階模態(tài)和二階模態(tài)對橋墩結構的穩(wěn)定性起到了控制性作用，其橫向、縱向的穩(wěn)定性分別由二階和一階模態(tài)控制；工況一～工況三作用下橋墩結構失穩(wěn)的主要類型均為結構縱向穩(wěn)定性，且臨界荷載系數(shù)滿足規(guī)范要求，處于穩(wěn)定狀態(tài)；溫差增大時，一階、二階的臨界荷載系數(shù)均減小，溫差作用對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小；墩高增大時，一階和二階的臨界荷載系數(shù)均減小，墩高變化對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小；相比于溫差和墩高變化，縱向和橫向風荷載變化對結構穩(wěn)定性的影響程度非常小，起不到?jīng)Q定性作用。

關鍵詞：連續(xù)梁橋墩；懸灌法；設計參數(shù)；穩(wěn)定性；數(shù)值分析

0引言

連續(xù)梁橋懸灌法施工技術因具有技術完善、受峽谷及氣候環(huán)境等影響小，并且所需施工面小，機械可多次重復使用等優(yōu)點，被廣泛地應用于橋梁修筑當中［1-2］。但在國內一些環(huán)境復雜惡劣的地區(qū)，連續(xù)梁橋懸灌法施工方法仍面臨著諸多挑戰(zhàn)，尤其對于超高墩，影響更大［3-4］。國內一些學者做了相關研究，張花［5］以某工程為研究對象，采用數(shù)值模擬的方法，分析了坡度、支座橫向間距和跨徑對橋梁穩(wěn)定性的影響，結果表明，坡度增大會降低橋梁穩(wěn)定性，增大支座橫向間距可以有效提高連續(xù)梁橋的整體穩(wěn)定性，增大跨徑基本對橋梁的整體穩(wěn)定性無影響。夏彬等［6］通過分析得出，設計人員要根據(jù)有限元軟件等多種技術詳細分析設計參數(shù)與橋梁穩(wěn)定性影響，并根據(jù)設計方法進行調整，以實現(xiàn)結構的安全穩(wěn)定。任超［7］以某連續(xù)剛構橋為研究對象，采用ANSYS軟件建立數(shù)值模型，分析了不同參數(shù)變化對高墩大跨連續(xù)剛構橋施工過程穩(wěn)定性影響的規(guī)律及原因。田國偉［8］以某大橋主橋為研究對象，分析了參數(shù)變化對結構撓度的敏感性影響，并根據(jù)參數(shù)情況對理論計算進行調整，使結構的線形和內力更加符合橋梁穩(wěn)定性要求。本文主要以某懸灌法施工連續(xù)梁橋超高墩穩(wěn)定性為研究對象，采用Midas Civil軟件建立橋墩數(shù)值模型，針對不同工況下橋墩結構的穩(wěn)定性展開了分析，并對結構穩(wěn)定性的參數(shù)影響規(guī)律進行了研究，研究結果可為同類橋梁工程的設計提供參考。

1 工程概況

某山區(qū)擬建大橋梁體為箱梁，總長度為368 m，采用（64+122×2+64）m布置形式，箱梁的頂板寬度為8.4 m，箱梁的底板寬度為6.2 m，梁高為4.2～8.5 m，橋墩高度為94～116 m。本文以116 m橋墩的超高墩為例，重點研究了在最大懸臂狀態(tài)（懸臂長度為62 m）與合龍狀態(tài)下橋墩結構的穩(wěn)定性。

2 數(shù)值建模

2.1 模型的建立

如圖1所示為采用Midas Civil軟件建立的橋墩模型，模型中橋梁跨度為126 m，兩端各取掉1 m，最終橋墩中心距離懸臂端為62 m，橋墩高度為116 m，整個“T”型結構一共劃分158個節(jié)點、155個單元。

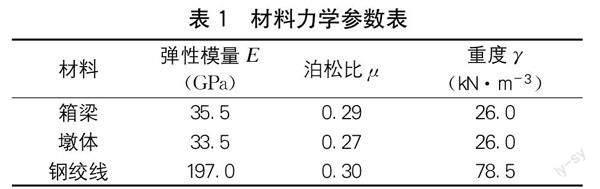
由于箱梁與橋墩分別采用C55、C35強度等級的混凝土，因此在模擬計算過程中箱梁、墩身及鋼絞線等材料的參數(shù)取值如表1所示。

2.2 工況設置

本文共設置3種不同計算工況。

（1）工況一：結構自重+施工時掛籃荷載。

（2）工況二：工況一+溫差+縱向風荷載。

（3）工況三：工況一+溫差+橫向風荷載。

在計算過程中風荷載按照《公路橋梁抗風設計規(guī)范》（CJTG/T D60-01-2004）中相關規(guī)定進行計算，溫差取10℃；掛籃等其它材料自重取值如表2所示。

3 數(shù)值結果分析

3.1 不同工況下結構穩(wěn)定性分析

工況一作用下結構一階、二階、三階和四階模態(tài)的臨界荷載系數(shù)和屈曲方向如表3所示。由表3可知，一階模態(tài)和二階模態(tài)是控制結構性穩(wěn)定的主要模態(tài)，而且結構的橫向穩(wěn)定性由二階模態(tài)控制，結構的縱向穩(wěn)定性由一階模態(tài)控制（見圖2）。工況一作用下的一階模態(tài)最小，對應的結構失穩(wěn)的主要類型為結構縱向穩(wěn)定性，按照規(guī)范中縱向和橫向臨界荷載系數(shù)均要＞4.0的規(guī)定可知，該橋墩結構在工況一作用下的穩(wěn)定性滿足規(guī)范要求。

如表4所示給出了工況二、工況三狀態(tài)下的臨界荷載系數(shù)和屈曲方向。由表4可知，結構的橫向穩(wěn)定性由二階模態(tài)控制，結構的縱向穩(wěn)定性由一階模態(tài)控制。工況二和工況三作用下均是一階模態(tài)最小，結構失穩(wěn)的主要類型均為結構縱向穩(wěn)定性，同時工況二、工況三作用下的臨界荷載系數(shù)均符合現(xiàn)行規(guī)范標準，即表明橋墩結構處于穩(wěn)定狀態(tài)。

此外，將工況一～工況三的臨界荷載系數(shù)進行對比分析可知，3種工況下，工況二的結構縱向穩(wěn)定性最差，工況三的結構橫向穩(wěn)定性最差。但無論施加縱向風荷載或者橫向風荷載，其穩(wěn)定性均主要由結構的縱向穩(wěn)定性控制。

3.2 參數(shù)敏感性分析

臨界荷載系數(shù)是反映結構穩(wěn)定性最直接的參數(shù)，本節(jié)主要通過研究改變溫差、墩高、橫向荷載和豎向荷載變化對臨界荷載系數(shù)的影響來反映相關參數(shù)的敏感性。

超高墩連續(xù)梁橋因墩身高度大、剛度小，非常易受溫差作用影響。如圖3所示，為結構臨界荷載系數(shù)隨溫差變化曲線，取溫差分別為5°、10°、15°、20°和25°進行研究分析。由圖3可知，隨著溫差的增大，一階和二階的臨界荷載系數(shù)均減小，相比于溫差為5°時，溫差分別為10°、15°、20°和25°時一階臨界荷載系數(shù)依次分別減少了6.8%、12.4%、16.1%和19.9%，對應二階臨界荷載系數(shù)依次分別減少了6.7%、11.9%、21.6%和28.4%，即隨著溫差的增大，一階臨界荷載系數(shù)減小幅度較小，二階臨界荷載系數(shù)減小幅度較大。由此可知，溫差作用對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小。因此，在溫差較大的地區(qū)進行高墩連續(xù)梁橋結構設計時，要充分考慮晝夜溫差對結構的橫向穩(wěn)定性影響，以免溫差作用對結構穩(wěn)定性產(chǎn)生的不良影響。

隨著墩身設計高度的增大，墩身截面積逐漸增大，且墩身高度一直是影響連續(xù)梁橋穩(wěn)定性重要的因素。如下頁圖4所示，為結構臨界荷載系數(shù)隨墩高變化曲線，取墩高分別為55 m、85 m、115 m、145 m和175 m進行研究分析。由圖4可知，隨著墩高的增大，一階和二階的臨界荷載系數(shù)均減小，相比于墩高為55m時，墩高分別為85 m、115 m、145 m和175 m時，一階臨界荷載系數(shù)依次分別減少了13.6%、29.3%、62.1%和76.3%，對應二階臨界荷載系數(shù)依次分別減少了17.2%、37.3%、61.5%和76.7%，即隨著墩高的增大，一階臨界荷載系數(shù)減小幅度較小，二階臨界荷載系數(shù)減少幅度較大。由此可知，墩高變化對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小。

由前節(jié)工況二和工況三可知，風荷載會對結構的穩(wěn)定性產(chǎn)生一定影響，為了分析風荷載變化對結構的穩(wěn)定性變化規(guī)律，下面主要通過增大風荷載的倍數(shù)來分析探討。

如圖5所示，為結構臨界荷載系數(shù)隨橫向風荷載變化曲線，取原始橫向風荷載和橫向風荷載分別增大0.5倍、1倍、1.5倍和2倍進行研究分析。由圖5可知，隨著橫向風荷載的增大，一階和二階的臨界荷載系數(shù)基本保持不變，相比于原始橫向風荷載，橫向風荷載分別增大0.5倍、1倍、1.5倍和2倍時一階臨界荷載系數(shù)依次分別減小了0.7%、1.4%、2.1%和2.7%，對應二階臨界荷載系數(shù)依次分別減少了0.6%、1.3%、2.2%和3.4%，即隨著橫向風荷載的增大，一階、二階臨界荷載系數(shù)均略微減少，橫向風荷載對橫向穩(wěn)定性的影響略大于對縱向穩(wěn)定性的影響。

如圖6所示，為結構臨界荷載系數(shù)隨縱向風荷載變化曲線，取原始縱向風荷載和縱向風荷載分別增大0.5倍、1倍、1.5倍和2倍進行研究分析。由圖6可知，隨著縱向風荷載的增大，一階和二階的臨界荷載系數(shù)基本保持不變，相比于原始縱向風荷載，縱向風荷載分別增大0.5倍、1倍、1.5倍和2倍時一階臨界荷載系數(shù)依次分別減小了1.4%、3.5%、5.7%和8.5%，對應二階臨界荷載系數(shù)依次分別減小了0.6%、2.0%、2.9%和4.1%，即隨著縱向風荷載的增大，一階、二階臨界荷載系數(shù)均略微減小，縱向風荷載對縱向穩(wěn)定性的影響略大于對橫向穩(wěn)定性的影響。

通過將風荷載變化與溫差、墩高變化進行對比可知，相比于溫差和墩高變化，縱向和橫向風荷載變化對結構穩(wěn)定性的影響程度都非常小，起不到?jīng)Q定性作用。

4 結語

本文主要以某懸灌法施工連續(xù)梁橋超高墩穩(wěn)定性為研究對象，通過采用Midas Civil軟件建立橋墩數(shù)值模型，針對不同工況下橋墩結構的穩(wěn)定性展開了分析，并對結構穩(wěn)定性的參數(shù)影響規(guī)律進行了研究，得到以下結論：

（1）一階模態(tài)和二階模態(tài)對橋墩結構的穩(wěn)定性起到了控制性作用，其中結構的橫向穩(wěn)定性主要由二階模態(tài)控制，結構的縱向穩(wěn)定性則由一階模態(tài)控制。工況一～工況三作用下橋墩結構失穩(wěn)的主要類型均為結構縱向穩(wěn)定性，且臨界荷載系數(shù)滿足規(guī)范要求，處于穩(wěn)定狀態(tài)。

（2）隨著溫差的增大，一階、二階的臨界荷載系數(shù)均減小，溫差作用對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小。

（3）隨著墩高的增大，一階和二階的臨界荷載系數(shù)均減少，墩高變化對結構的橫向穩(wěn)定性影響較大，對結構的縱向穩(wěn)定性影響相對較小。

（4）相比于溫差和墩高變化，縱向和橫向風荷載變化對結構穩(wěn)定性的影響程度非常小，起不到?jīng)Q定性作用。

參考文獻：

［1］李雪強.用機制砂和摻合料雙摻配制C55混凝土百米高程泵送懸灌梁施工技術［J］.施工技術，2020，49（S1）：1 402-1 404.

［2］黃勤勞.高墩大跨徑連續(xù)剛構橋懸灌法施工關鍵技術［J］.鐵道建筑技術，2020（10）：110-112，130.

［3］閔 帥.巫鎮(zhèn)高速公路橋梁預應力混凝土連續(xù)剛構懸灌施工技術［J］.工程技術研究，2022，7（2）：76-77.

［4］李揚奇.橋梁工程中大跨度箱形連續(xù)梁菱形掛籃懸灌施工技術［J］.低碳世界，2021，11（4）：244-245.

［5］張 花.設計參數(shù)變化對連續(xù)梁橋整體穩(wěn)定性影響分析［J］.蘭州工業(yè)學院學報，2019，26（4）：20-23.

［6］夏 彬，戚中洋.連續(xù)梁橋設計參數(shù)變化對整體穩(wěn)定性的影響分析［J］.建筑技術開發(fā)，2020，47（10）：129-130.

［7］任 超.大跨度懸灌連續(xù)梁施工中線形控制技術的應用［J］.智能城市，2021，7（6）：51-52.

［8］田國偉.懸灌法施工條件下超高墩連續(xù)梁穩(wěn)定性分析［J］.福建交通科技，2021（6）：95-98.

作者簡介：葉羽升（1988—），工程師，主要從事高速公路監(jiān)理、檢測工作。