高動態井下環境的OSELM 定位算法研究

竇占樹, 崔麗珍?, 羅海勇, 洪金祥

(1.內蒙古科技大學 信息工程學院,內蒙古 包頭 014010;2.中國科學院 計算技術研究所,北京 100190)

0 引言

近年來,煤礦智能化建設[1-3]成為當下研究的熱點,對煤礦井下目標的定位精度[4]有了更高的要求。 與此同時,各種井下無線定位技術[5-6]得到快速發展。 基于WiFi 的井下定位技術[7-9]由于其特有的定位優勢,已經在工業生產中得到了廣泛應用。井下環境復雜多變[10-11],狹長的井下通道、粗糙的巷道幫壁、工作人員的實時移動、大量的粉塵和復雜的井下基礎設施等都使得井下通信環境時刻處于變化之中,導致定位模型精度降低。 在復雜多變的煤礦井下環境及時并準確地獲取井下作業人員的位置顯得非常重要。 基于位置指紋的定位技術由離線和在線階段組成。 離線建庫階段[12]的主要工作是收集樣本點RSS 的值和對應的坐標,用于構建指紋數據庫。 在線定位階段[13]需要選取合適的定位算法,通過對比用移動終端采集到的RSS 值和指紋數據庫[14]中存儲的RSS 值,數據庫中對應的最相似參考點的坐標就是待定位目標點的坐標。 離線數據庫主要用于訓練定位模型,使模型具有更強的泛化能力。將在線數據輸入到用離線數據訓練好的模型中,最終得到待定位目標點的坐標。 煤礦井下定位技術主要包括WiFi 技術、UWB 技術[15]和藍牙技術[16]等。基于WiFi 的井下定位技術能夠滿足井下定位的精度需求。

本文將在線順序極限學習機(Online Sequential Limit Learning Machine,OSELM)算法[17-20]用于井下定位,利用OSELM 算法的在線學習能力實現對定位模型的在線實時更新,同時對OSELM 算法進行改進。 實驗表明,經改進的OSELM 算法能夠有效提高模型的定位精度。

1 OSELM 算法

本文選擇3 層OSELM 神經網絡結構。 輸入層有4 個神經元,代表4 個AP 點提供的RSSI 信號強度值;隱藏層有155 個神經元;輸出層有2 個神經元,輸出對應的(X,Y)坐標。 OSELM 網絡結構如圖1所示。

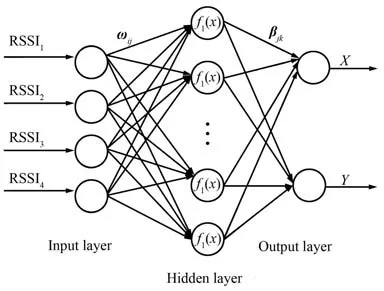
圖1 OSELM 網絡結構Fig.1 OSELM network structure

f1(x)為隱藏層節點激活函數,wij為輸入層第i個神經元與隱藏層第j個神經元間的連接權值,βjk為隱藏層第j個神經元與輸出層第k個神經元間的連接權值。 通常,SELM 由N個訓練樣本、p個輸入層節點、L個隱藏層節點和q個輸出層節點組成,N個采樣節點的坐標為:

在采樣節點處接收到的來自v個AP 無線接入點的信號強度值為:

OSELM 網絡表達式為:

式中,f(·)表示激活函數;βj為隱藏層第j個神經元與輸出層間的連接權值矩陣;wi=[wi1,wi2,…,wip]為輸入層與隱藏層間的連接權值矩陣;bj為第j個隱藏層神經元偏置矩陣。 式(3)可簡化為:

式中,H 表示隱藏層輸出矩陣;C 表示期望輸出矩陣。 隱藏層與輸出層間的連接權值 β 能夠通過求解方程組最小二乘解得到,即:

式中,‖·‖表示范數,對應的解為:

式中,H?為H 的廣義逆矩陣,當OSELM 網絡應用于回歸預測領域時,對應的定位誤差為:

2 改進的OSELM 算法

利用OSELM 的在線學習能力,能很好地解決因井下環境高動態變化導致模型精度下降的問題。但該模型只是完成了在線更新的過程,并沒有對新增數據的質量、有效性進行評估。 本文對OSELM算法引入權重項ω進行改進。

在權值ω的設置中,應考慮以下3 點:

① 采集新增數據的參考點數占實驗區域內所有參考點數的比例大小。 采集新增數據的參考點都是均勻分布在實驗區域的情況下,如果采集新增數據的參考點數較多,應該給予相對較大的權重來對模型進行更新。 反之,應該給予相對較小的權重。用ω1表示采集新增數據的參考點覆蓋率的影響。

② 采集新增數據的時間先后順序。 當有多批增量數據依次到達定位模型時,需要根據增量數據到達的時間先后順序給予權重上的不同。 采集新增數據的時間點距離在線定位的時間點越近,含有的有用信息越多,應該給予更大的權值。 用ω2表示新增數據時效性的影響。

③ 當考慮2 個影響因素時,將時效性和覆蓋率改進實驗進行融合,做融合性改進實驗。 融合性權重ω3可表示為:

3 實驗驗證

3.1 算法對比實驗

在煤礦井下環境進行實驗區域的部署。 采集數據的煤礦井下巷道空間狹長且曲折,同時有各種機械設備,環境較為復雜多變。 選定80 m×3 m×3 m的實驗區域,離線階段每隔1 m 部署一個參考點,共部署81 個參考點。 在10,30,50,70 m 處分別部署1 個WiFi AP 熱點,共采集4 050 條數據。 在線階段每隔5 m 進行數據采集,共17 個參考點,采集850 條數據。 實驗通過增加通道內測試人員的走動,增加干擾噪聲的同時改變障礙物的位置,來達到使通道內的通信環境發生變化的目的。 實驗場景如圖2所示。

圖2 實驗場景Fig.2 Experimental scene

為驗證所提算法能有效解決井下環境高動態變化導致模型精度降低的問題,本文采用2 個實驗對所提算法性能進行驗證。

實驗1:在實驗區域內相同環境下采集離線建庫數據和在線定位數據。 實驗2:離線建庫數據與實驗1 相同,采集在線定位數據時,需要改變實驗環境,即在同一實驗區域不同環境下采集離線和在線數據。

定位精度是衡量本文實驗結果的重要指標,主要是衡量通過定位算法得到的待定位目標點的坐標估計值與真實值之間的接近程度。 定位精度越高,說明待定位目標點的坐標估計值與真實值之間的接近程度越高,定位算法的優越性越大。

3.1.1 實驗1:3 種算法對比實驗

SVM,ELM 和OSELM 三種算法的定位精度對比如圖3 所示。

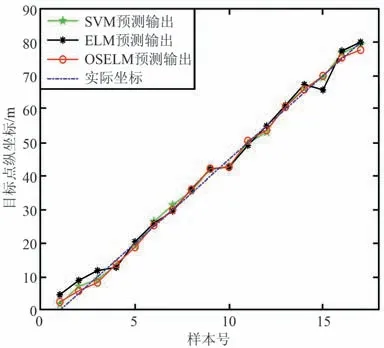
圖3 定位精度對比Fig.3 Comparison of positioning accuracy

SVM,ELM 和OSELM 三種定位算法的均方根誤差(Root Mean Squared Error,RMSE)對比如表1 所示。

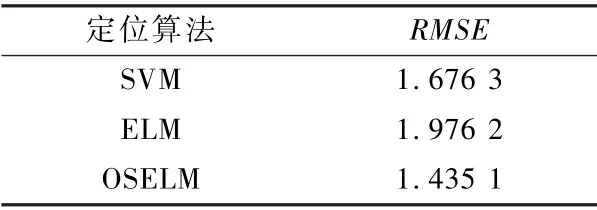
表1 3 種算法的RMSE 對比Tab.1 Comparison of RMSE of three algorithms單位:m

由圖3 可知,3 種算法的預測值和真實值擬合程度均較高。 對比3 種算法的RMSE 可知,OSELM算法比SVM 算法低0.241 2 m,OSELM 算法比ELM算法低0.541 1 m,定位誤差均在2 m 內,滿足復雜井下環境的定位精度需求。

3.1.2 實驗2:3 種算法對比實驗

SVM,ELM 和OSELM 三種算法的定位精度對比如圖4 所示。

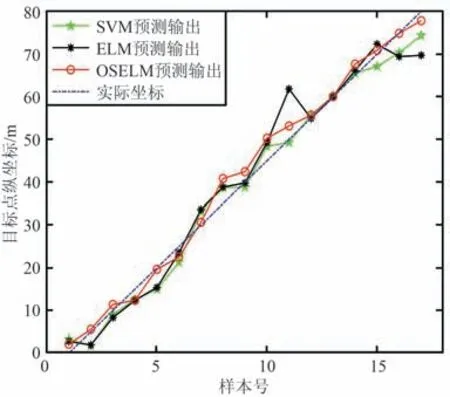
圖4 定位精度對比Fig.4 Comparison of positioning accuracy

實驗環境發生變化后,SVM,ELM 和OSELM 三種算法的RMSE 對比如表2 所示。

表2 3 種算法的RMSE 對比Tab.2 Comparison of RMSE of three algorithms單位:m

由圖4 可知,3 種算法預測輸出值和真實坐標值的擬合程度與實驗1 相比,定位精度都有所降低。對比表2 和表1 可以看出,SVM,ELM 和OSELM 三種算法的RMSE 分別增大了1.755 8,1.889 1,0.668 6 m。實驗環境變化后,SVM 和ELM 定位算法的RMSE變化較大,OSELM 定位算法的RMSE 變化較小。 因此,OSELM 算法更適合用于解決WiFi 井下動態定位問題。

3.2 算法改進實驗

在實驗區域內共采集9 批數據:1 個初始訓練數據集Train-data、7 個不同時間采集的增量數據集Incredata1~7 和1 個測試數據集Test-data。 其中,增量數據集Incredata1~4 用于參考點覆蓋率的改進實驗;增量數據集Incredata5~7 用于新增數據時效性的改進實驗。

(1)采集新增數據的參考點覆蓋率權重對定位模型精度的影響

用Incredata1~4 分別對模型進行更新,權值計算公式為:

當考慮權重時,由式(9)可知Incredata1~4 的權重分別為1/2,1/3,1/5,1。 當不考慮權重時,ω值為1。 用Train-data 訓練初始模型,分別用Incredata1~4 對模型進行增量學習。 最后用Test-data 對模型進行測試。 統計在不同誤差距離下的定位精度。 采集新增數據的參考點覆蓋率權重對定位精度的影響如圖5 所示。

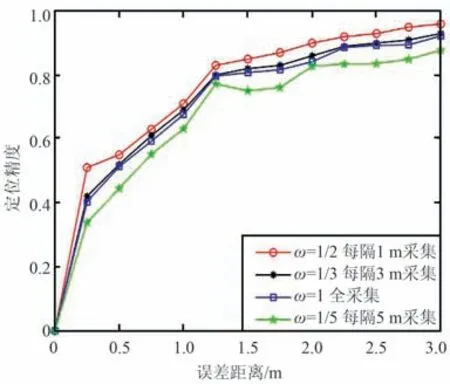
圖5 采集參考點覆蓋率權重對定位精度的影響Fig.5 Effect of acquisition reference point coverage weights on positioning accuracy

用Incredata1~4 分別對模型進行增量學習,在誤差距離為1,2,3 m 的情況下,定位精度對比如表3所示。

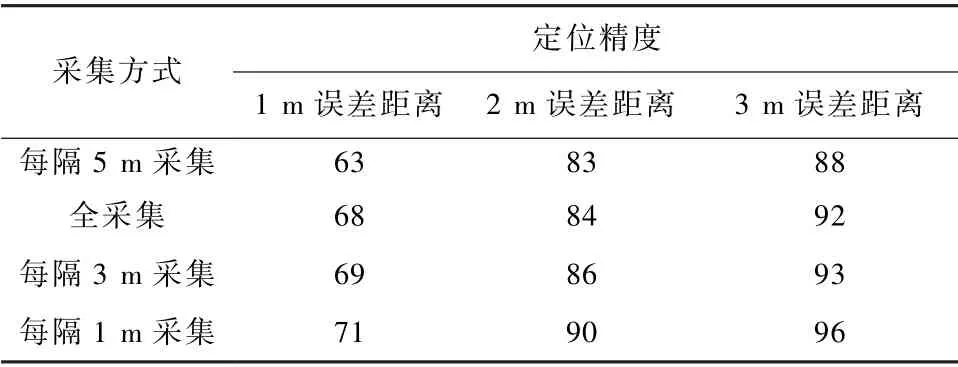
表3 定位精度對比Tab.3 Comparison of positioning accuracy單位:%

由表3 可知,用每隔1 m(權值為1/2)和3 m(權值為1/3)的方式采集到的數據對模型進行增量學習的定位精度較高,因為每隔1,3 m 采集到的數據量剛好適用于對模型進行增量學習,使得模型泛化能力更強。 而按全覆蓋(權值為1)和每隔5 m(權值為1/5)的方式進行數據的采集,采集到的數據量過多和過少,易使模型出現過擬合和欠擬合現象,導致模型精度降低。 用每隔1 m 采集到的數據對模型進行增量學習,定位精度最高,大大降低了數據采集工作量,提升了實驗效率。

(2)增量數據時效性權重對模型精度的影響

考慮到采集增量數據的時間先后順序,為增量數據賦予時效性權重對模型進行在線增量式學習,計算公式為:

式中,T0為離線數據采集時間點;Τ1為在線數據采集時間點;t為增量數據采集時間點,t∈[T0,T1]。

考慮時效性權重時,由式(10)可知,Incredata5~7的權重分別為:ω5=2/7,ω6=3/7,ω7=4/7。 有3 批數據用于時效性改進實驗,共有6 種增量數據到達情況,增量順序1~6 分別為:(5,6,7),(5,7,6),(6,5,7),(6,7,5),(7,5,6)和(7,6,5)。 對比6 種不同增量順序情況下定位誤差在1,2 m 時的定位精度,如表4 所示。

表4 定位精度Tab.4 Positioning accuracy單位:%

由表4 可知,在增量順序為(5,6,7)的情況下,定位精度最高。 定位誤差在1,2 m 時,定位精度分別達到了88%和95%,按照采集增量數據的時間先后順序對模型進行增量學習,會使模型定位精度最高。

當考慮時效性權重時,按照增量數據采集的時間先后順序(5,6,7)對定位模型進行增量學習。 不考慮時效性權重時,把增量數據(5,6,7)作為一個整體進行增量學習。 統計在3 m 誤差距離下的定位精度。 引入時效性權重對定位模型精度的影響如圖6 所示。

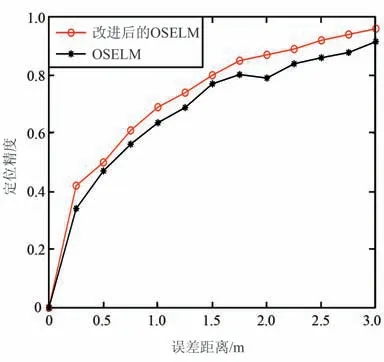
圖6 時效性權重對定位精度的影響Fig.6 Effect of timing weights on positioning accuracy

OSELM 算法和引入時效性權重進行改進的OSELM 算法在誤差距離為1,2,3 m 時的定位精度對比如表5 所示。

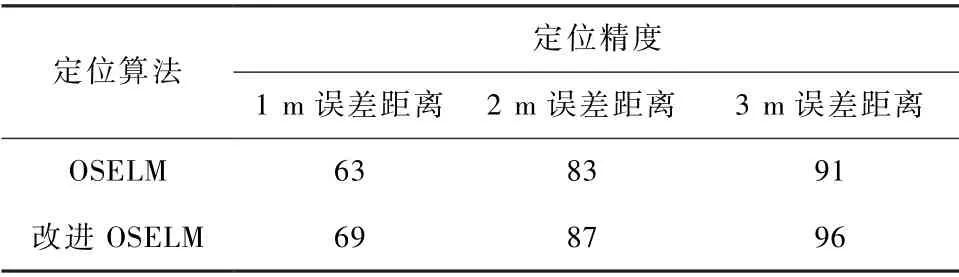
表5 定位精度對比Tab.5 Comparison of positioning accuracy單位:%

由表5 可知,在誤差距離為1,2,3 m 的情況下,引入時效性權重進行改進的OSELM 算法與OSELM算法相比,定位精度分別提高了6%,4%,5%。 在3 m 誤差距離內,為增量數據引入時效性權重能有效提高定位模型精度。

(3)同時考慮2 個影響因素時,做融合性改進實驗

采用乘法取權值的方式進行權值的計算,權值計算公式為:

根據式(9)計算出Incredata1~7 的權值,各增量數據權值如表6 所示。

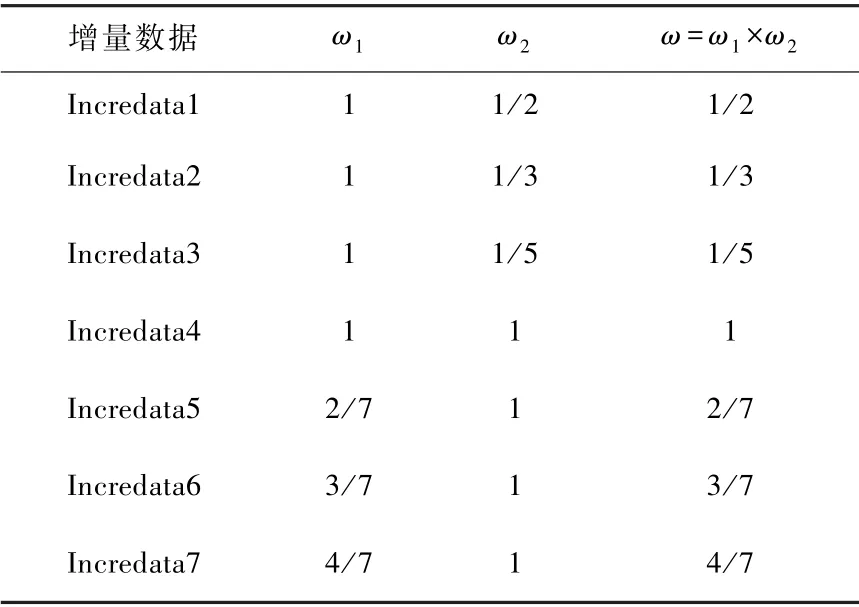
表6 各增量數據權值Tab.6 Weights of incremental data

首先,用Train-data 訓練初始模型。 默認不考慮權重的情況下,權值為1,所以Incredata4 是不考慮權重的情況。 其次,Incredata1 的權值最大,為1/2,因此在融合性改進實驗中,選擇用權值最大的Incredata1 對模型進行在線增量式學習。 最后,用Testdata 對模型進行測試。 所得定位結果與BP,ELM,OSELM 三種算法定位精度進行對比,如圖7 所示。

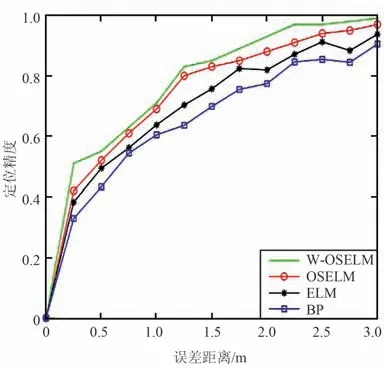
圖7 定位精度對比Fig.7 Comparison of positioning accuracy

考慮2 種因素進行改進的OSELM 算法和BP,ELM,OSELM 三種算法在1,2,3 m 誤差距離下定位精度對比,如表7 所示。

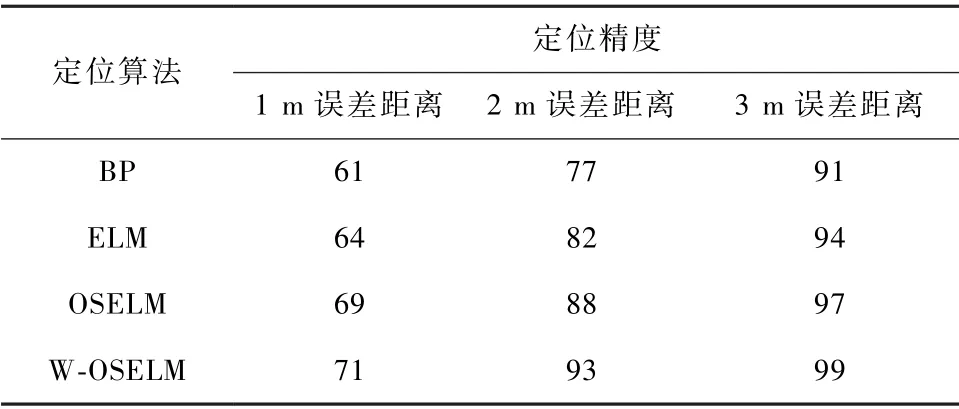
表7 定位精度對比Tab.7 Comparison of positioning accuracy單位:%

綜合考慮2 種因素的基于改進的OSELM 算法與其他3 種算法對比,定位精度最高。 在1,2,3 m 誤差距離下,定位精度分別達到了71%,93%,99%。在3 m 誤差距離范圍內,給予新增數據融合性權重,能夠提高模型定位精度。

4 結束語

本文將OSELM 算法用于井下定位,同時從新增數據時效性和采集新增數據的參考點覆蓋率兩方面以及綜合考慮這兩方面因素對OSELM 算法進行改進。 實驗結果表明,實驗環境變化后,與SVM 和ELM 算法相比,OSELM 算法對動態環境有更強的適應能力。 同時,為OSELM 算法給予時效性權重,能夠提高定位模型精度。 每隔1 m 進行增量數據的采集與全覆蓋采集方式相比,模型精度更高,同時大大降低了數據采集工作量。 綜合考慮兩方面因素對OSELM 算法進行改進,與BP,ELM,OSELM 算法進行對比,顯著提升了定位模型精度。 因此,在OSELM 算法基礎上加入權重項的考慮,能夠有效提高定位模型精度,所提OSELM 及其改進算法均可行有效。