Effect of kinetic ions on the toroidal double-tearing modes

Ruibo Zhang(張睿博) Lei Ye(葉磊) Yang ChenNong Xiang(項農) and Xiaoqing Yang(楊小慶)

1Hefei Institutes of Physical Science,Chinese Academy of Sciences,Hefei 230031,China

2University of Science and Technology of China,Hefei 230026,China

3Center for Integrated Plasma Studies,University of Colorado at Boulder,Boulder,Colorado 80309,USA

Keywords: double-tearing modes,kinetic ions,coupling effect

1.Introduction

Double-tearing modes (DTMs) can be excited in a reversed magnetic shear configuration, due to the two rational surfaces with the same helicity.Different from the singletearing mode (STM), the two tearing modes on neighboring rational surfaces can be coupled with each other and the linear growth rate of the DTMs is much larger than that of the STM.In a slab plasma, the resistivity scaling of the DTMs(γ～η1/3)[1]is weaker than that of the STM (γ～η3/5).[2]Hereγandηare the growth rate of the tearing mode and the resistivity, respectively.Moreover, nonlinear DTMs can generate strong sheared flows, release large bursts of kinetic energy, and cause the off-axis sawtooth crashes,[3]which may give rise to a major disruption.Therefore, it is important to understand the mechanism of DTMs and to develop methods to suppress the DTMs in tokamaks.Since DTMs are formed by the coupling of tearing modes to each other on two rational surfaces, it is natural to anticipate that the DTM instability can be mitigated by either suppressing or decoupling the tearing modes on two rational surfaces.It has been found that toroidicity[4,5]has stabilizing effects on the STM.On the other hand,shear flows,[6-10]diamagnetic effects[11,12]and external current drives[13,14]can help to decouple the two rational surfaces in a DTM.

It is difficult to analytically predict behaviors of the tearing mode due to its multi-scale property, and the kinetic effects of ions near the tearing layer may be important.In the past few years,many theoretical and numerical investigations have pointed out that kinetic ions are important in evolution of the STM.[15-20]Theoretical analyses and numerical simulations found that trapped energetic ions have a stabilizing effect on DTMs.[21,22]An investigation of the kinetic ions effect on DTMs has been carried out with the gyrokinetic code GTC.It was found that the kinetic ions destabilize the DTMs in toroidal geometry without toroidal coupling.[23]With energetic ions,the off-axis sawtooth oscillations induced by DTMs were observed in the TFTR,[3]CHS[24]and HL-2A[25]experiments.

In our previous work,[5]the gyrokinetic particle-in-cell code GEM was employed to study the toroidal effects and kinetic ion effects on STM with the hybrid gyrokinetic ion/fluid electron model.A new field solver in toroidal geometry has been developed for the simulation of low-nmodes in tokamaks.It was found that kinetic ions,mainly the passing particles,have a stabilizing effect on the STM.In the present study,we continue to investigate the DTMs in tokamak geometry using GEM.The main focus is on the the influence of kinetic ions on the coupling of DTMs between the two rational surfaces.

The remaining part of this paper is organized as follows.The simulation model and basic equations are briefly described in Section 2.The effects of kinetic ions on the DTMs are studied in Section 3.The conclusion is drawn in Section 4.

2.Physical model

The gyrokinetic ion/fluid electron hybrid model is employed in this paper to study the (m= 3,n= 1) DTMs in the toroidal geometry.In the hybrid model, the ions are described by the gyrokinetic equation, the particle trapping and the finite-orbit-width effects are included.The electrons are treated as a massless isothermal fluid.Recently, the hybrid version of GEM has been extended to low-nmodes by developing a new field solver, and applied to the simulation of the(2,1) STM in toroidal geometry.[5]Here for convenience we give a brief description of the fluid model for electrons.More details can be found in Refs.[5,26,27]and references therein.

The electron continuity equation is written as

withu‖e0andδu‖ebeing the equilibrium electron parallel flow and the perturbed electron parallel flow, respectively.The perturbed electron pressure isδ pe⊥=δ pe‖=neδTe+Teδne,δTeandδneare perturbed electron temperature and perturbed electron density, respectively.The last two terms on the lefthand side of Eq.(1) are associated to the toroidal geometry.The toroidal pressure term ?(δ pe⊥+δ pe‖) arises from the guiding-center magnetic drift in a low-βplasma,[28]and the last term from the compressibility of theE×Bdrift.

The parallel vector potentialA‖can be evolved by withj‖=δ j‖i-en0δu‖ebeing the parallel perturbed current.The parallel ion currentδ j‖iis calculated from the ion distribution function.

The electron parallel flow velocityδu‖eused in the electron continuity equation, i.e., Eq.(1), is obtained from Ampere’s equation

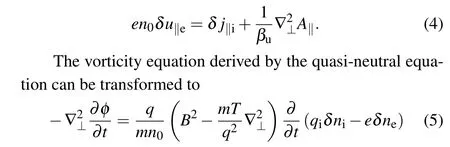
using the Pad′e approximation.The second term on the righthand side of Eq.(5) indicates the finite-Larmor-radius (FLR)effect.

The main closure relation for this fluid electron model is the linearized isothermal condition for the perturbed electron temperature,[29]

This isothermal condition is derived from the electron drift kinetic equation by assumingω ?k‖vTe,whereωis the characteristic frequency of the fluctuations,vTeis the electron thermal speed, andk‖is the parallel wave number.The coupling effect of different poloidal harmonics in toroidal geometry is preserved in all the following simulations.

3.Simulation results

In this section, the (m,n)=(3,1) DTMs in a tokamak plasma are studied by gyrokientic particle-in-cell(PIC)simulation.A magnetic equilibrium with concentric circular fluxsurfaces is used, with an on-axis magnetic fieldB0=1.6 T,major radiusR0=1.82 m and inverse aspect ratioε=a/R0=0.25,wherea=0.46 m is the minor radius.The safety factor profile is set as

（1）重視新科技在金融行業的應用。對于清華大學數字貨幣進校園，我認為應該鼓勵，支持學校等機構積極探索新技術的應用。

withλ= 1,r0= 0.412,δ= 0.303,A= 3, andqcis varied for different separations (ds) of the twoq= 3 rational surfaces, as shown in Fig.1.The density profile is set to be constant asn0i=n0e= 1.3×1019m-3.The temperature profiles areTe(r)=-T0e(r/a-0.45)+T0eandTi(r)=-T0i(r/a-0.45)+T0ifor electrons and ions.TheT0e=0.1 keV is fixed.T0ican be varied to study the effect of a finite ion temperature.In the following the resistivityηand the growth rateγare normalized toη0=B0/en0e=0.77Ωm andωc=eB0/mi=7.74×107Hz,respectively.

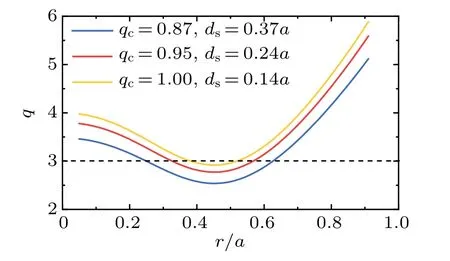
Fig.1.Safety factor profiles for different ds by varying qc.

3.1.Simulations of DTMs with cold ions

Firstly, we present the simulation result for the DTMs with cold ions (T0i=10-3keV andL-1Ti=0), where the kinetic effects of ions are in fact excluded.Figure 2 shows the typical 2D mode structure of DTMs for the perturbed electric potentialδφand perturbed vector potentialδA‖on the poloidal cross section withη=2×10-5.It can be observed that the mode structure has an in-out asymmetry due to the toroidal magnetic field.

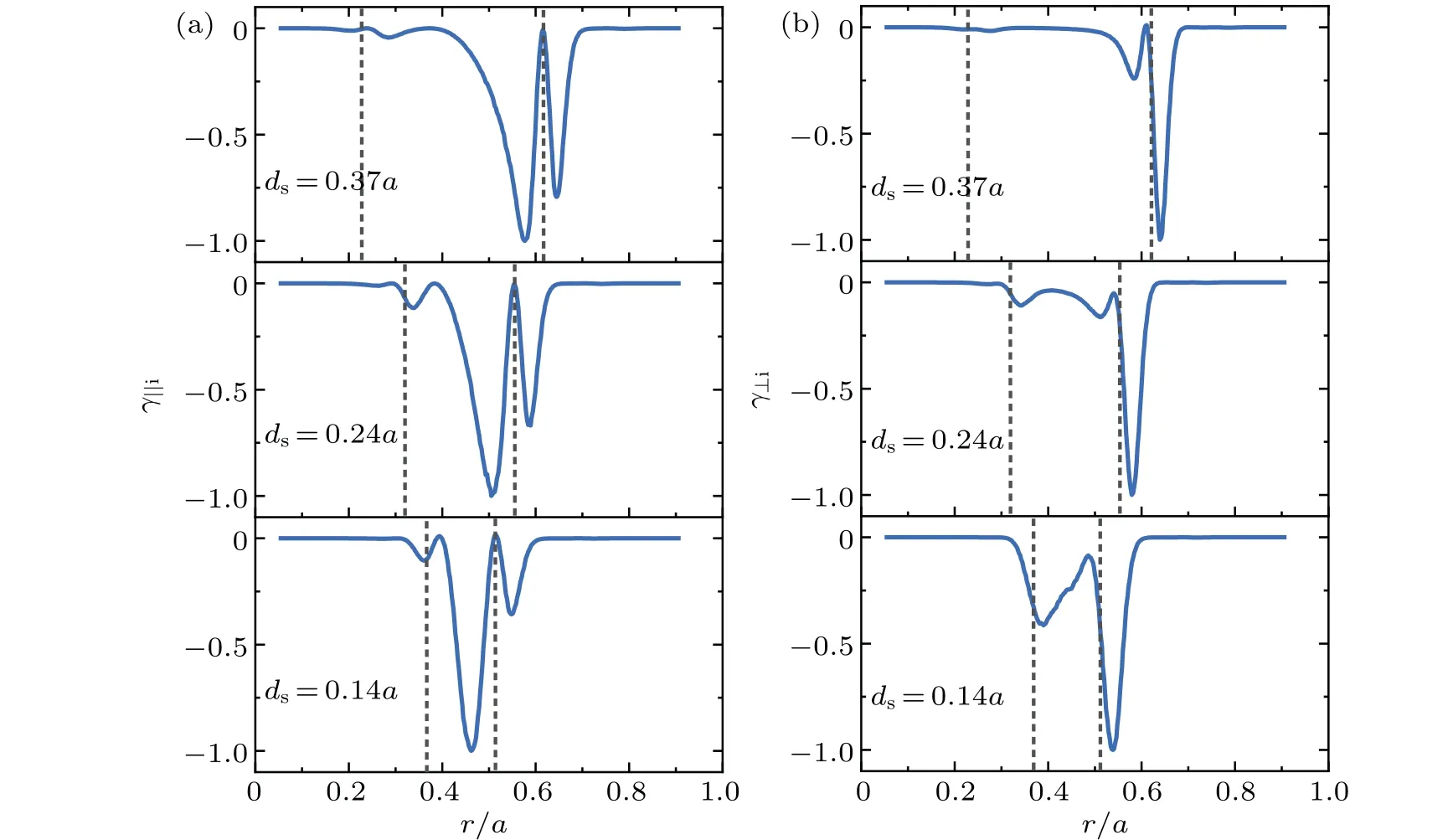
As we know, the separation of the two rational surfaces is a key factor affecting the coupling effect between the two rational surfaces.Thus, several simulations have been performed with differentdsand the corresponding radial mode structures ofδφare plotted in Fig.3.It can be seen that for a larger separation ofds=0.37a, the mode structure can be considered as a simple superposition of the two STMs located on each rational surface, respectively.However, asdsis decreased,the coupling effect between the two rational surfaces is stronger,and the mode amplitude in the coupling region can be significantly increased.The variation of radial modes structure between the two rational surfaces can also be used as a criterion for the coupling effect of the DTMs.

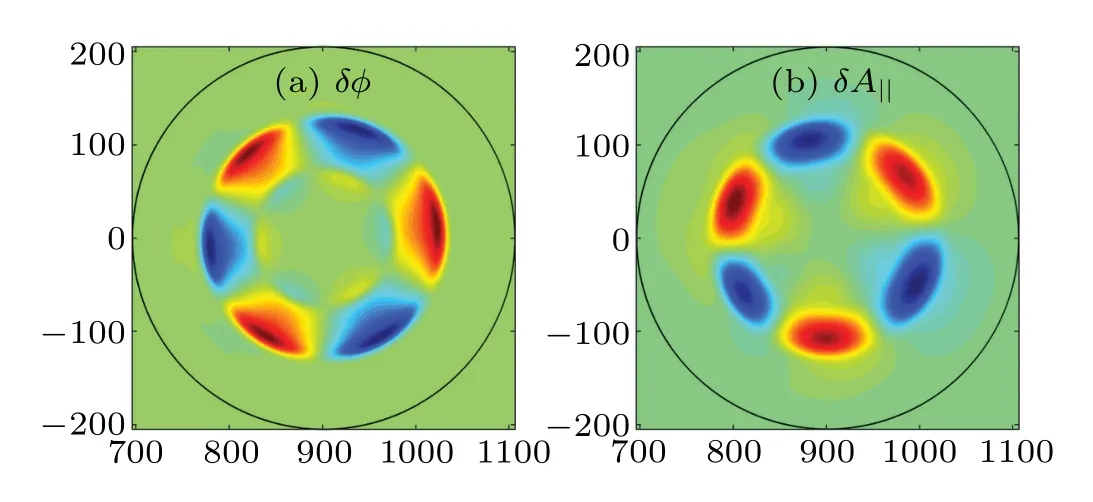
Fig.2.Mode structure of DTMs with ε =0.25 and η =2×10-5.

Fig.3.The radial mode structures of δφ for ds =0.37a, ds =0.24a and ds=0.14a for η =2×10-5 with T0i=1×10-3 keV.All the profiles are normalized to the their maximum absolute values.The mode amplitude in the coupling region is increased by decreasing ds.

Fig.4.The dependence of growth rate on η with and without toroidal pressure term.

For givends=0.24a,the growth rate of the DTMs for differentηis shown in Fig.4.Two resistivity scalings,γ～η0.9andγ～η1/3can be found in the small and large resistivity limit, respectively.The scaling for largeηis consistent with the DTM scaling,which is also consistent with the numerical results presented in Refs.[22,30].However, the scaling for small is larger than that of the STM(γ～η3/5).We find that this discrepancy is associated with the toroidal effect,specifically the electron toroidal pressure termδ pein Eq.(1).This term arises from the guiding-center magnetic drift in a toroidal magnetic field.As plotted by red squares in Fig.4, when the toroidal pressure term is neglected in the simulation,the scaling of STM(γ～η3/5)is recovered in smallηlimit.

The mode structure of DTMs also changes withη.Figure 5 shows the radial structures ofδφfor three different value ofη.It can be seen that the mode amplitude in the coupling region increases withη.Similar results have been shown in Fig.3,where the enhanced coupling is induced by decreasingds.Nevertheless,for a fixed separation of the two rational surfacesds, the width of the STM on each rational surface can be broadened by increasingη.Therefore, the interaction between the two modes can also be enhanced.This process is also consistent with the different resistivity scalings in twoηlimits,as shown in Fig.4.

Fig.5.The radial mode structures for η =5×10-6, η =2×10-5 and η =1×10-4 with T0i=1×10-3 keV.All the profiles are normalized to the their maximum absolute values.The mode amplitude in the coupling region is increased with η.

3.2.Effect of kinetic ions on the DTMs

In this subsection, the kinetic effects of thermal ions on the DTMs are investigated numerically.Firstly, the dependence of the growth rates of the DTMs onηfor cold and thermal ions are compared in Fig.6.It can be seen that the growth rate of the DTMs can be effectively reduced by thermal ions,the suppression effect increases withη.Moreover,with thermal ions,the DTMs scaling,γ～η1/3,can be extended to smaller resistivity ofη ≈1×10-5.This modification to the resistivity scaling indicates an enhanced coupling of DTMs between the two rational surfaces induced by thermal ions.

Fig.6.The dependence of growth rate on η for cold (T0i = 1×10-3 keV) and thermal (T0i =0.1 keV) ions with L-1Ti =0.It can be seen that the growth rate of the DTMs can be effectively suppressed by thermal ions and the suppression effect increases with η.

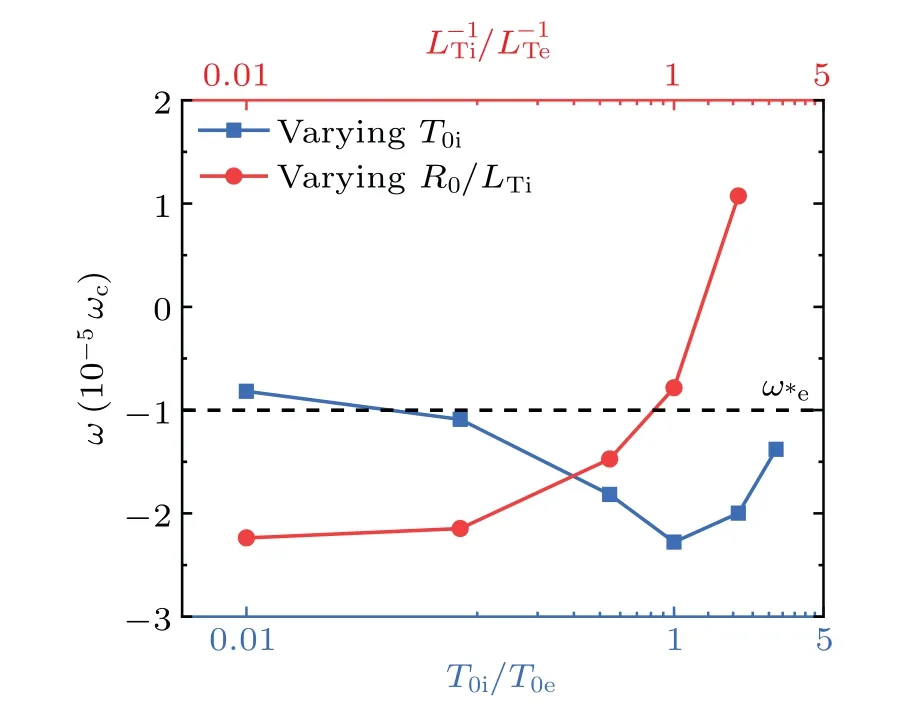
Fig.7.The dependence of growth rate and frequency on T0i.

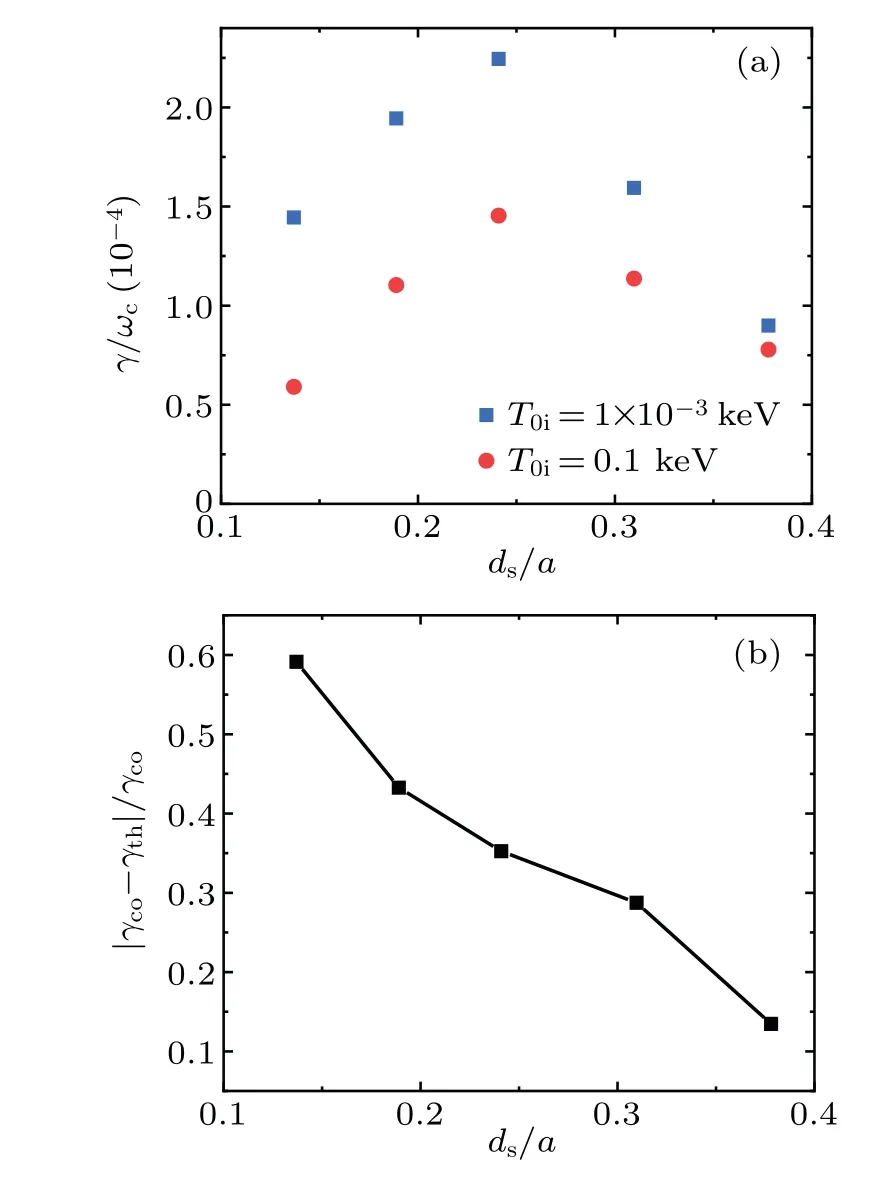
Fig.8.(a)The growth rate of DTMs for cold and thermal ions for different ds.(b) The stabilization effect of kinetic ions decreases as ds increases.The superscripts ‘co’ and ‘th’ represent cold and thermal ions,respectively.

To further illustrate the effect of thermal ions on the DTMs,especially the coupling effect between the two rational surfaces, the simulations of the DTMs with different separations of the two rational surfaces are carried out.The simulation results for the growth rate are plotted in Fig.8.From Fig.8(a), it can be found that withdsincreasing, the growth rate increases at first and then decreases,which is independent of ion temperature.In Fig.8(b), it can be seen that the stabilization effect of thermal ions decreases asdsincreases.As we have shown before,the coupling effect can be enhanced asdsdecreases.This indicates that the stabilization effect of thermal ions on DTMs depends on the the coupling effect between the two rational surfaces.In Fig.9, the radial mode structures of the DTMs for differentdswith cold and thermal ions are plotted.It can be seen that whendsis large(ds＆gt;0.24a),the coupling effect between the two rational surfaces is weak,thermal ions can increase the mode amplitude in the coupling region.This enhancement effect increases with the coupling effect.Whendsis small (ds＆gt;0.24a), the coupling effect is strong and the resistivity scaling isγ～η1/3,the coupling enhancement effect of thermal ions becomes weaker.

The above results suggest that thermal ions can suppress the growth of the DTMs.The suppression effect of kinetic ions becomes stronger with the enhancement of the coupling between rational surfaces.On the other hand,kinetic ions can enhance the coupling effect between the two rational surfaces whendsis large.However, further investigations should be carried out to explore the physical dynamics of the interaction between kinetic ions and the DTMs.

It is known that the effect of kinetic ions includes the FLR effect and the effect of a finite radial magnetic drift (vD) in a toroidal magnetic field.It has been found that the FLR effect is not important in the STM instability especially for largeη[5,31]due to the fact that the ion gyro radius is much smaller than the width of the STM.The kinetic ions can affect the STM mainly through the magnetic drift in toroidal geometry.Since the width of the DTMs is much larger than that of the STM,we can speculate that the kinetic ions also affect the DTMs mainly through the magnetic drift.This can be illustrated by Table 1.

Table 1.FLR effect and magnetic drift effect on the DTMs growth rates for η =5×10-5.The growth rates are normalized to the value from the cases with cold ions(T0i=1×10-3 keV).

Fig.9.The radial mode structures for T0i =1×10-3 keV and T0i =0.1 keV for ds =0.37a,0.24a,and 0.14a.The profiles are normalized to their maximum absolute values.

It has been shown that the kinetic ions can provide either an energy source or sink for tearing modes.[17]To gain further insight into the energy exchange between kinetic ions and the DTMs,the simulation results are studied by analyzing energy transfer between the ions and the wave field.Similar analysis has been given in our previous work for the STM.[5]Here we focus on the kinetic ion effect on the coupling of the two rational surfaces for the DTMs.A brief introduction to the numerical diagnostic of Joule heating is given in the following,and more details can be found in Ref.[5].The energy-like equation can be derived as

As shown in Table 2, for thermal ions, bothγ‖iandγ⊥ihave dumping effect on the DTMs.The perpendicular Joule heating rate is larger than the parallel Joule heating rate for both trapped and passing ions.This is different from the STM result where the parallel Joule heating rate is dominant.The contribution of the passing ions to the damping rate is much larger than that of trapped ions in both the parallel and perpendicular directions.

In order to investigate the influence of kinetic ions on the coupling between the two rational surfaces,the radial distributions of ion Joule heating for differentdsare plotted in Fig.10.It can be seen that the ion Joule heating rate is mainly distributed around the outer rational surface and the coupling region.For the distribution ofγ‖i(Fig.10(a)), the peak on the right side of the outer rational surface decreases with the decrease ofds,which means that the relative amplitude between the two rational surfaces is increased.Forγ⊥i(Fig.10(b)),the damping rate can be significantly increased between the two rational surfaces and cause substantial damping of the DTMs asdsis decreased.Therefore, one can conclude from the above observations that thermal ions can effectively impact the DTMs through the energy exchange between ions and wave fields around the outer rational surface and the coupling region.On the one hand, thermal ions can enhance the coupling effects of the DTMs.On the other hand, the enhanced coupling of the DTMs can in turn induce stronger energy exchange owing to the ion dynamics in the coupling region.The consequent result of such a wave-particle interaction is the suppression of the DTMs growth rate and extending of the resistivity scalingγ～η1/3to smallerη.

Table 2.The Joule heating rate of passing and trapped ions for T0i =10-3 keV and T0i=0.1 keV when η =2×10-5.The superscripts‘T’and‘P’represent trapped and passing ions,respectively;γ is the heating rate.

4.Conclusion

In this work, the effects kinetic ions on the linear DTMs are studied by using the GEM code with a gyrokinetic ion/fluid electron model.The toroidal effect can decrease the growth rate of the DTMs and increase the resistivity scaling for smallηthrough the toroidal pressure term in the electron continuity equation.Thermal GK ions can decrease the growth rate of the DTMs significantly and change the resistivity scaling by enhancing the coupling effect of the two rational surfaces.The suppression effect increases with the ion temperature and the decrease of separation of the two rational surfaces.The mechanisms of the ions affecting the DTMs are studied through energy transfer analysis.It is found that the DTMs can be effectively affected by thermal ions through the energy exchange between ions and wave fields around the outer rational surface and the coupling region.Thermal ions can enhance the coupling effects of the DTMs.On the contrary,the enhanced coupling of the DTMs can in turn induce stronger energy exchange owing to the ion dynamics in the coupling region.

Acknowledgements

This work was supported by the National MCF Energy R&D Program of China (Grant No.2019YFE03060001),the National Key R&D Program of China (Grant No.2017YFE0300406), and the National Natural Science Foundation of China(Grant Nos.11975272 and 11905257).Y.Chen is supported by the SciDAC Center Advanced Tokamak Modeling Environment(AToM)(Grant No.DE-SC0017992).The numerical calculations in this work were performed on the ShenMa High Performance Computing Cluster in Institute of Plasma Physics, Chinese Academy of Sciences, and resources of the National Energy Research Scientific Computing Center (NERSC), which are supported by the Office of Science of the U.S.Department of Energy(Grant No.DEAC02-05CH11231).