改進傅里葉域轉換的分子性質預測方法仿真

唐 漸，劉玉清

(西南醫科大學醫學與信息工程學院，四川 瀘州 646000)

1 引言

在生物信息學的大力推動下，分子作為關鍵的活性物質[1]，受到了物理、化學、生物、材料、計算機科學等多領域的高度關注，并逐漸演變為眾多領域的熱點話題。生物分子所具備的性質[2]不僅決定著國民的生命健康與安全，而且對生物自身的應用與發展有著極其深遠的影響，因此，有必要研究出一種快速且易于實現的分子性質預測方法。

近幾年，相關領域研究人員在分子性質預測方向取得了較好的成就。比如：譚露露等人[3]采用多特征融合圖卷積方法，就分子的生物活性展開預測；蘇敏儀等人[4]應用應用機器學習方法，針對藥物分子的解離速率常數，構建預測模型。盡管以上方法已經取得了較好的應用成果，但在預測的性質類別上存在一定局限性。

為了解決以上問題，本文以圖神經網絡為基本算法，提出分子性質預測方法。在數據處理任務中，以圖神經網絡[5]的表現最為突出，結合圖數據與神經網絡。作為深度神經網絡的泛化形式，圖神經網絡現已廣泛應用于生命科學、知識圖譜等重大領域。對于本文研究成效而言，圖神經網絡依據與分子結構之間的依賴關系，為分子性質分析與預測提供了強大的建模助力，有助于加強模型預測性能；卷積優化圖神經網絡能賦予分子結構圖由淺至深的特征，聚合更新的內部傳輸機制使圖卷積神經網絡更具靈活性，通過加強節點間的信息聚合與傳遞，有助于提升不規則圖數據的分子性質預測準度。

2 圖神經網絡的構建與優化

2.1 圖神經網絡

根據圖形種類的頂點-邊結構，構建(賦權)無向圖[6]、(賦權)有向圖[7]、循環圖[8]等多種圖類型數據，作為神經網絡的輸入項來獲取輸出結果，即圖神經網絡。假設任意類型圖G的頂點集合是V，邊集合是E，則圖G的表示形式如下所示

G=(V，E)

(1)

其中，圖G邊的方向有無主要取決于頂點間的方向依賴關系；圖頂點即神經網絡的節點。

已知節點v的特征xv關聯于節點的真實標簽，若想根據圖G的部分標記節點，預測出未標記節點的標簽，則采用下列表達式界定各網絡節點

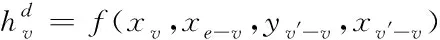
(2)

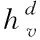
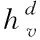
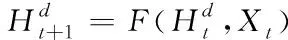
(3)

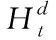
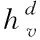
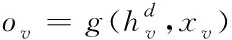
(4)

其中，g表示輸出函數公式，即前饋全連接神經網絡層。

2.2 圖卷積神經網絡

分子結構相對復雜，不規則數據較多，導致傳統圖神經網絡無法處理圖中的非規則數據與邊緣信息，擾亂分子節點分布形式，影響節點間關系的精準描述。因此，利用傅里葉變換方法[11]在圖神經網絡中引入譜卷積，構建圖卷積神經網絡。

運用圖拉普拉斯矩陣[12]的特征逆矩陣UT，通過下列表達式把輸入節點v轉換至傅里葉的域φ中

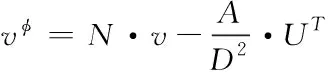
(5)

其中，逆矩陣UT已作歸一化處理；vφ表示傅里葉域中的輸入節點；N表示單位矩陣；D、A分別指代度量矩陣與鄰接矩陣。

利用下式卷積操作節點vφ與卷積核：

J=U·γ·UTvφ

(6)

式中，U表示圖拉普拉斯矩陣的特征矩陣。

為降低卷積運算難度，采用下列切比雪夫多項式實現卷積操作，獲取近似卷積結果

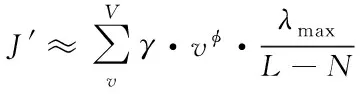
(7)

式中，λmax表示圖拉普拉斯矩陣L的最大特征值。

實際的輸出結果應是多維節點特征，而非一維項。因此結合鄰接矩陣A與節點自身特征，通過下列表達式進行更新，得到多維的節點特征x′v

x′v=f(Xt，A)=sigmoid[(A+N)·Xt·ω(0)]

(8)

式里，sigmoid為激活函數[13]；ω(0)是網絡層的連接權值。

3 圖卷積神經網絡下的分子性質預測

將聚合、更新兩階段作為圖卷積神經網絡的內部傳輸機制，加強網絡各節點間的信息聚合與傳遞，提高預測精準度。因此此傳輸機制下圖卷積神經網絡的分子性質預測流程如圖1所示。

具體實現步驟描述如下：

圖1 分子性質預測流程

1)融合分子結構圖與圖卷積神經網絡：設定圖G頂點v(即網絡節點)為分子結構的原子，邊為結構化學鍵，則圖節點的特征xv即原子特征，包含原子的元素種類、度數、電荷量等多種特征；圖連邊的特征xe-v即化學鍵特征，包含化學鍵的類型、位置、空間屬性等特征。

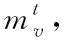
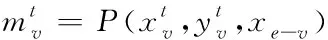
(9)

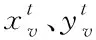
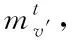
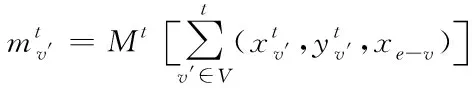
(10)

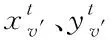
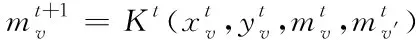
(11)

4)預測分子性質：在反復的聚合與更新過程中，結合所有原子得到整個圖G結構的表征形式，即分子結構向量G′，如下所示

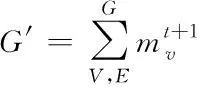
(12)

將向量G′作為網絡的待輸入圖類數據，則基于原子v的圖卷積神經網絡輸出結果Y如下所示，即根據由原子特征與化學鍵特征構成的分子結構，得到的分子性質預測結果為

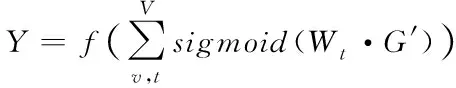
(13)

式中，Wt表示第t層的網絡學習矩陣算法。

(14)

由此推導出下列損失函數Loss的界定公式

(15)

其中，Xe-v表示化學鍵特征xe-v的所有關聯項。

為使各變量相對于圖卷積神經網絡參數均具備可微屬性[15]，利用激活函數sigmoid將上列損失函數Loss界定式改寫成下列表達式

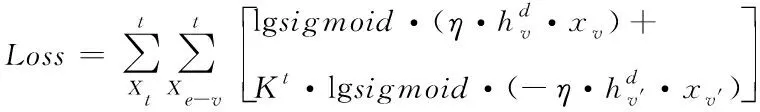
(16)

其中，η表示激活函數的修正系數。

4 實驗分析

4.1 數據集的選取與處理

從開源的GEO數據集[16]中選取含有十萬以上不規則分子的子集。該子集中的分子屬性種類及性質均值如表1所示。

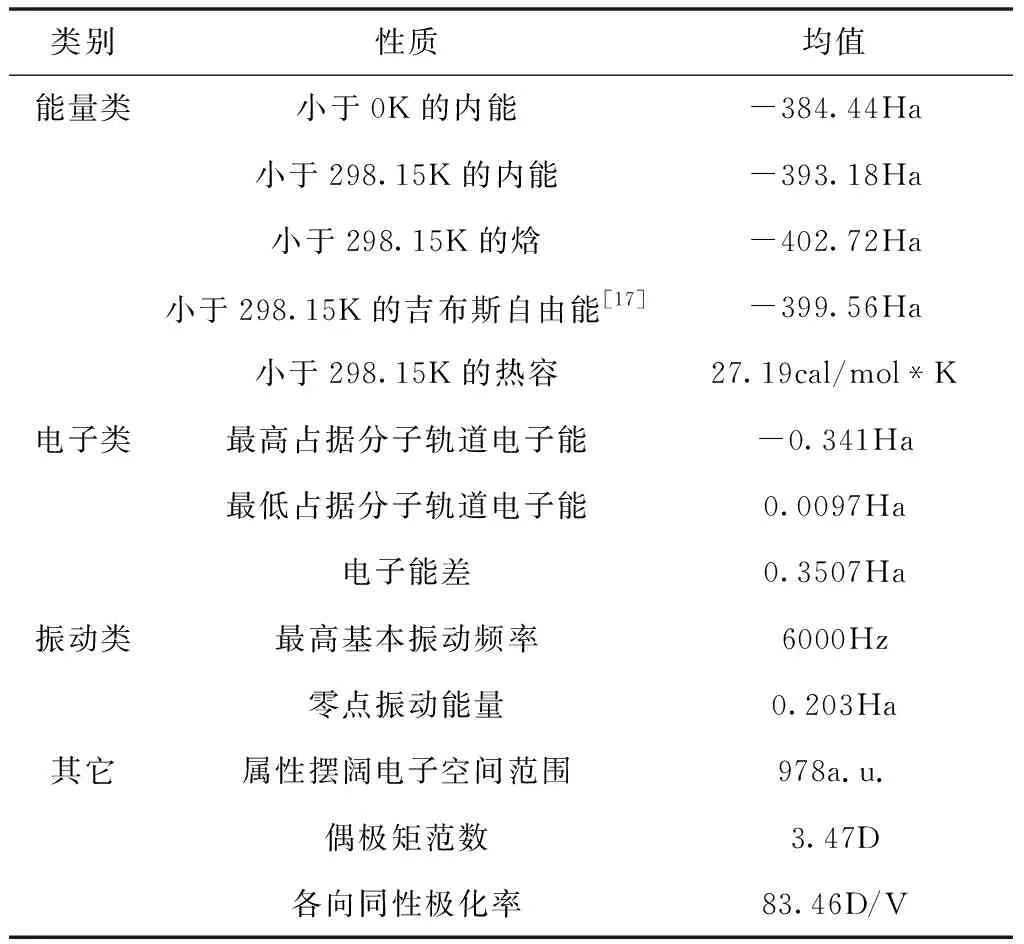
表1 實驗用數據集中分子相關信息

為避免子集中分子發生過擬合現象[18]，歸一化處理[19]所選數據集，降低分子性質的預測誤差，提高訓練效率。利用數據集80%的訓練樣本獲取最優網絡參數后，綜合評價研究方法、文獻[3]的基于特性融合圖卷積方法的分子生物活性預測方法以及文獻[4]的基于機器學習的分子性質預測方法的精準性、泛化性、遷移性等預測能力。

4.2 分子性質預測精度

不同分子屬性種類的預測精度變化趨勢如圖2所示。

根據圖2可以看出，本文針對復雜分子結構的不規則數據與邊緣信息，利用傅里葉變換方法引入譜卷積而構建出的圖卷積神經網絡，使誤差評估指標均值不超過0.15，決定系數始終位于0.999以上，能滿足實際應用中的精準度需求。所得實驗結論足以說明，該方法不僅在精準預測分子性質方面取得了出色的表現，而且對于大規模數據集具有較好的處理能力。

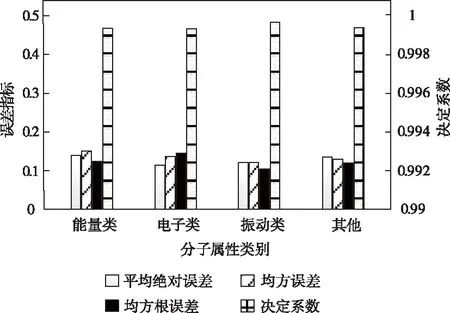
圖2 預測精準性評價結果示意圖

4.3 分子性質預測的泛化性分析

方法泛化性[20]的檢測目的主要是驗證預測方法對小數據集是否具備較強的學習能力。從實驗用數據集中隨機選取出四種不同規模的數據子集，利用本文方法對四個數據集分別展開分子性質預測，由均方根誤差指標進行評估，分析模型的泛化性能。為突顯本文方法的優越性，將基于特性融合圖卷積方法的分子生物活性預測方法以及基于機器學習的分子性質預測方法作為對比項，不同方法的均方根誤差數據變化趨勢如圖3所示。

由圖3可知，各方法的均方根誤差值均隨著數據集規模的變小而增大；兩個對比方法的上升趨勢近似于線性，增幅較大；而本文的圖卷積神經網絡則依據聚合與更新的內部傳輸機制，通過加強各原子間的信息聚合與傳遞能力，有效抑制了均方根誤差值的增加幅度，即便是50MB數據量的小規模數據集，指標值也沒有超過0.25。

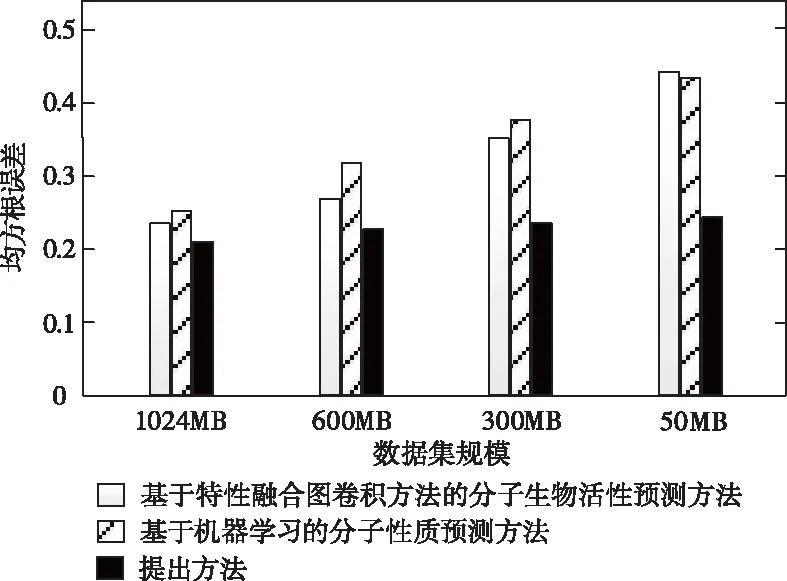
圖3 預測模型泛化性評價結果示意圖

4.4 分子性質預測的遷移性分析

方法遷移性的檢測目的主要是驗證預測方法是否能將從小規模數據集習得的知識應用于其它數據集上。以選取的50MB數據集作為學習樣本，檢驗三種方法對整個實驗用數據集的分子性質預測能力，各方法的評估指標數據變化趨勢如圖4所示。

對比大規模樣本數據集的預測結果可知，本文方法的誤差類指標值略有上升，決定系數指標值略有下降；盡管學習樣本數據量大幅減少，但相較于對比方法的高誤差值、低擬合度，本文通過融合分子結構圖、聚合鄰域信息、更新原子結構等階段，既實現了對原子特征的表示學習，也取得了整個圖形數據的結構，因此誤差指標均值僅有0.218，決定系數相對趨近于0.999，依舊具有較為優越的預測能力。

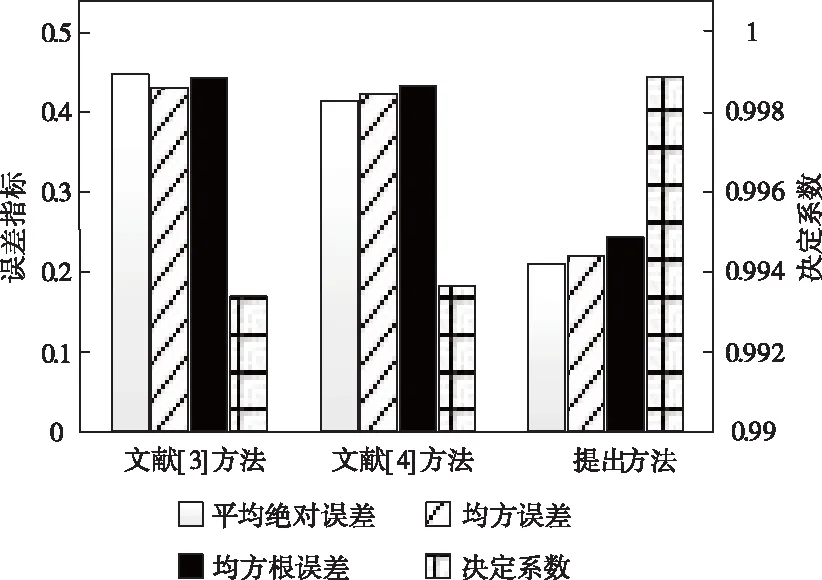
圖4 預測模型遷移性評價結果示意圖

5 結論

在材料、藥物、食品等領域中，多元化分子的性質與屬性研究，對拓寬所屬物料的應用前景、賦予更高的實踐價值具有重要的指導作用。為探尋性能更優越的物料，準確預測出未知結構的分子性質是必要且重要的。隨著人工智能領域飛速發展，利用計算機相關技術來處理大規模數據信息的手段已相對成熟。因此，本文嘗試將人工智能技術中的神經網絡與分子性質預測課題相結合，并取得了不錯的成效。

為進一步推動人工智能技術與物料分子研究的融合深度與研究進程，為相應領域的候選物料提供更精準的分子結構參考依據，將以下幾個方面作為今后深入探究的重點：選取的實驗數據集相對單一，應就其它數據集展開仿真，檢驗方法的適用性；分子結構分為同構與異構兩種形式，應繼續學習分子理論知識，從同構分子圖與異構分子圖角度，完善圖神經網絡算法；應深入探索跨領域時分子的化學、物理、藥理等屬性對預測結果的影響，使預測任務更具針對性，擴大方法的應用范圍。