基于PID控制的多軸聯動數控機床運動誤差補償

史 燕，吳 璞，2

(1. 太原工業學院機械工程系，山西 太原 030008；2. 中北大學機械工程學院，山西 太原 030051)

1 引言

數控機床的加工精度在制造業和裝備業不斷發展的背景下逐漸提高，目前常用的數控機床大部分都屬于兩軸聯動，在加工過程中，該類數控機床的運動軌跡都是一個方向，容易出現參數不匹配、負載擾動和機械系統效率低的問題，加大了數控機床的跟隨誤差和運動輪廓誤差[1]。為了解決兩軸聯動數控機床的問題，提出了多軸聯動的數控機床，被廣泛地應用在精密模具、航海和航天等加工領域中[2]。受伺服系統動態響應特性、電氣控制和機械轉動等因素的影響，多軸聯動的數控機床在加工運動過程中無法避免運動誤差的產生，因此，需要研究數控機床運動誤差補償方法。

陳維范[3]等人首先檢測了數控機床X進給軸熱誤差和主軸熱誤差，采用最小二乘法根據檢測的誤差建立熱誤差模型，對數控機床在運動過程中產生的誤差展開實時補償，該方法沒有構建數控機床的運動軌跡方程，在橢圓測試過程中獲得的誤差補償曲線與理想區域之間的偏差較大，存在誤差補償精度低的問題。郭世杰[4]等人在齊次坐標變換方法和多體系統理論的基礎上構建誤差空間模型，結合遺傳算法和牛頓迭代法完成誤差補償，該方法在螺旋旋轉體控制過程中無法控制多軸聯動數控機床的加工精度，表明該方法的誤差補償效果差。黃智[5]等人利用熱成像儀確定數控機床的溫度敏感點，在敏感點處設置溫度傳感器，獲取數控機床在工作狀態下的熱特性數據，根據獲取的數據構建誤差模型，結合神經網絡實現誤差補償，該方法的運動誤差補償結果受多軸聯動數控機床運動速度的影響較大，存在適應性差的問題。

為了解決上述方法中存在的問題，提出多軸聯動的數控機床運動誤差補償方法。

2 數控機床運動分析

2.1 數控機床聯動運動軌跡

受阻尼、剛度和摩擦等因素的影響，在實際加工過程中，數控機床在工作狀態下的實際輸出與預期輸出不一致，數控機床在不同運動狀態下產生的誤差也不相同，多軸聯動數控機床在上述狀態下容易出現運動誤差。

用Ke表示位置編碼器產生的脈沖數；Kp表示控制器在工作狀態下產生的位置增益；用Kd表示數控機床的數模轉換系數；用Kb表示反電動勢常數；用Ra表示電樞回路在系統中對應的電阻。為方便多軸聯動數控機床運動誤差的計算，多軸聯動的數控機床運動誤差補償方法通過二階模型描述多軸聯動的數控機床系統[6，7]，如圖1所示。

圖1中，D代表的是微分算子；J描述的是轉動慣量；Kn代表的是數控機床在工作狀態下的速度反饋系數；Ks為速度調節器在多軸聯動數控機床系統中產生的增益；Kq為電機力矩常數。

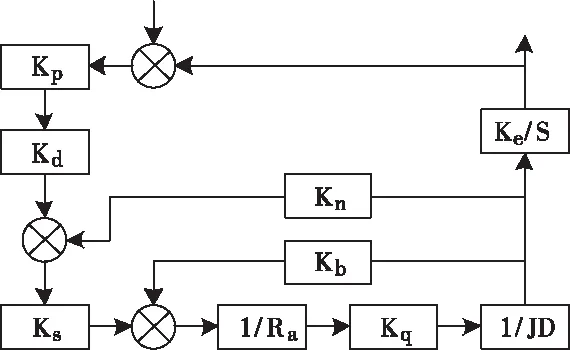
圖1 多軸聯動的數控機床系統簡化模型

根據圖1構建多軸聯動的數控機床系統的速度環控制模型E(S)

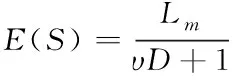
(1)

式中，υ代表的是時間常數；Lm代表的是單位電壓在數控機床系統中的電機轉速，其計算公式分別如下

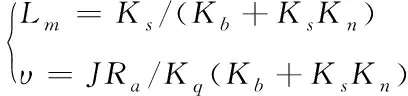
(2)

用Hk表示位置控制開環在多軸聯動數控機床系統中的傳遞函數，其表達式如下

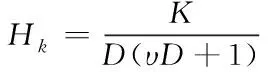
(3)

式中，K=KpKdKmKe代表的是位置閉環控制在多軸聯動數控機床系統中產生的開環增益。通過二階模型H(S)簡化數控機床系統的閉環傳遞函數

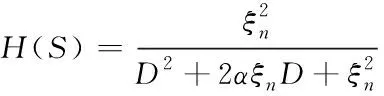
(4)

式中，ξn=(K/υ)1/2、α=(Kυ)-1/2/2。

分別用xi(t)=Tcos(ξt)、yi(t)=Tsin(ξt)表示多軸聯動數控機床x軸和y軸在加工過程中的輸入，其對應的穩態輸出xo(t)、yo(t)可通過下式計算得到

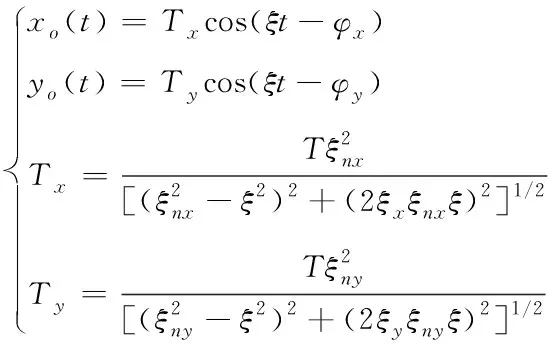
(5)

式中，ξ代表的是軌跡對應的角速度；Tx、Ty分別代表的是x軸和y軸在數控機床系統中的輸出幅值；ξnx、ξny分別代表的是x軸和y軸在數控機床系統中的固有頻率；φx、φy分別代表的是x軸和y軸在數控機床系統中產生的滯后相位；ξx、ξy分別表示x軸和y軸對應的阻尼比。

根據上述計算結果，構建如下多軸聯動數控機床的運動軌跡方程[8，9]

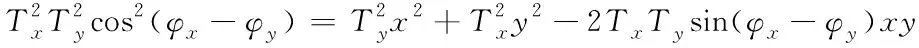
(6)

令αx=αy=α、ξnx=ξny=ξn、φx=φy，可將上式轉化為

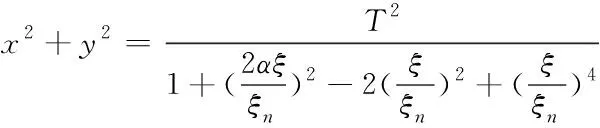
(7)

2.2 運動誤差

研究表明，機械因素和電氣因素都會影響多軸聯動數控機床的運動誤差，運動誤差由兩個部分構成，分別是跟隨誤差和輪廓誤差[10，11]。根據多軸聯動的數控機床運動軌跡計算其運動誤差。

用Q1(xi，yi，zi)、Q2(xi+1+m，yi+1+m，zi+1+m)表示曲線運動對應的坐標點；分別用rkx、rky、rkz，φkx、φky、φkz表示x軸、y軸和z軸在多軸聯動數控機床運動過程中產生的跟隨誤差分量和輪廓誤差分量，此時存在下式

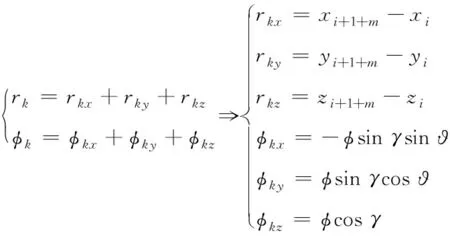
(8)

式中，rk代表的是跟隨誤差；φk代表的是輪廓誤差；γ代表的是曲線運動位置在t時刻與z軸之間存在的夾角；?代表的是運動曲線在t時刻與y軸之間存在的夾角。

在式(8)的基礎上計算誤差φ：

φ=-φsinγsin ?sin ?+

φsinγcos ?cos ?+φcosγcosγ

(9)

令Rx=φsinγsin ?、Ry=φsinγcos ?、Rz=φcosγ、Vx=sin ?、Vy=cos ?、Vz=cosγ，結合上述公式，通過下式計算多軸聯動的數控機床運動誤差φ

φ=-RxVx+RyVy+RzVz

(10)

3 運動誤差補償

采用PID控制器[12，13]對上述過程計算得到的運動誤差進行補償。將運動誤差φ(t)作為PID控制器的調節對象，用yout(t)表示數控機床的輸出值，用rin(t)表示數控機床的設定值，此時運動誤差φ(t)可以表示為φ(t)=rin(t)-yout(t)。

用Tc表示PID控制器的微分時間常數，在PID控制器中對運動誤差φ(t)展開微分操作、積分操作和比例操作，獲得PID控制器的控制信號i(t)

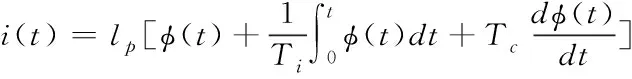
(11)

式中，Ti為PID控制器的積分時間常數；lp描述的是比例系數。

在拉氏變換的基礎上構建如下傳遞函數：

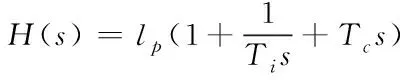
(12)

針對PID控制器中的微分，所提方法用兩個采樣點對誤差變化曲線上的連線斜率進行表示，針對PID控制器中存在的積分，所提方法用分割矩形面積表示

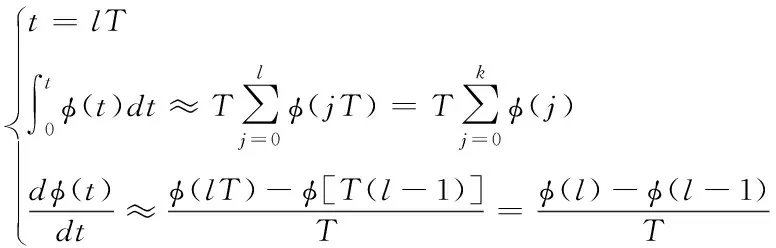
(13)

式中，φ(l-1)、φ(l)分別代表的是第l-1個采樣時刻和第l個采樣時刻多軸聯動數控機床的運動偏差。

用lD表示數字式PID控制器的微分系數，此時可將數字式PID控制器表示為

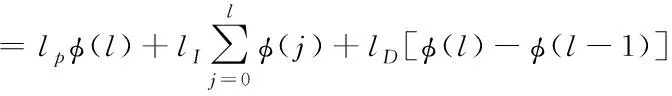
(14)

式中，lI描述的是積分系數；lp代表的是比例系數。

為了避免PID控制信號過大或過小，提高誤差補償精度，所提方法在PID控制器優化過程中引入粒子群優化算法[14，15]，對lI、lp、lD展開優化，具體優化過程為：

1)初始化處理粒子群算法中的相關參數。

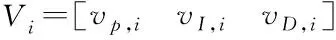
3)每個粒子通過適應度函數獲得對應的適應度值Ki。

4)獲取每個粒子和全部粒子在尋優過程中的最佳位置Xibest、Xzbest，通過適應度函數獲得對應的適應度值Kibest、Kzbest。

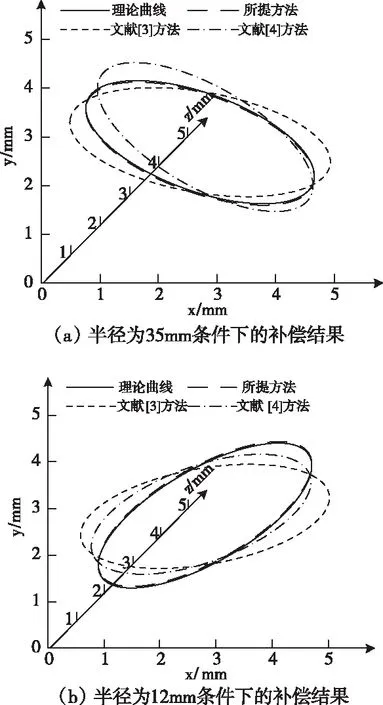
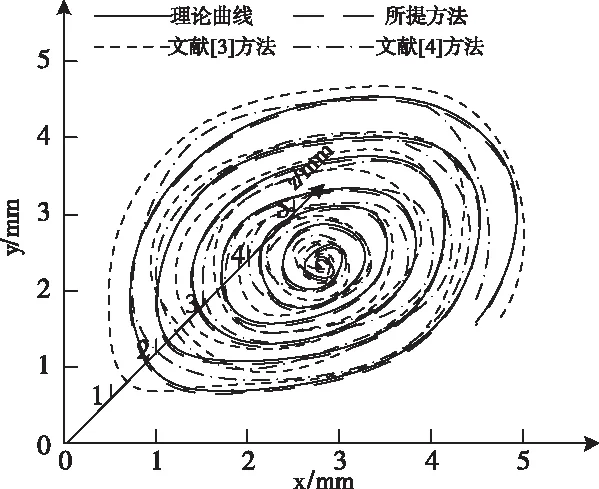
當Ki

5)通過下式完成粒子速度的更新

Vi=ωVi+v1rand()×(gbesti-Xi)

+rand()×(zbesti-Xi)

(15)

式中，ω代表的是慣性因子；zbesti、gbesti分別代表的是全部粒子和每個粒子對應的最優適應度值；v1、v2代表的是學習因子；rand()表示隨機數，在區間[0，1]內取值。

利用下式完成粒子位置的更新

Xi=Xi+Vi

(16)

6)設置粒子群優化算法的最大迭代次數M，當粒子群優化算法滿足最大迭代次數時，輸出優化后的PID控制器參數，完成參數優化。

將多軸聯動的數控機床運動誤差輸入優化后的PID控制器中，完成運動誤差補償。

4 實驗與分析

為了驗證多軸聯動的數控機床運動誤差補償方法的整體有效性，需要對其展開測試，將文獻[3]方法和文獻[4]方法作為對比方法。在MATLAB軟件中展開數控機床運動誤差補償測試，表1為數控機床基本參數。

表1 數控機床基本參數

將上述參數輸入至仿真軟件中，圖2為模擬界面。

使數控機床運動速度保持不變，采用所提方法、文獻[3]方法和文獻[4]方法在半徑35mm和12mm條件下展開橢圓測試，結果如圖3所示。

圖2 仿真界面

由圖3可知，在不同半徑條件下，所提方法補償后的數控機床運動輪廓與理論曲線基本相符，而文獻[3]方法和文獻[4]方法補償后的數控機床運動輪廓與理論曲線之間存在較大偏差，因為所提方法通過粒子群算法優化了PID控制器，利用優化后的PID控制器補償多軸聯動數控機床的運動誤差，降低了數控機床在工作過程中產生的顫動造成的誤差。

圖3 橢圓測試結果

在相同測試平臺中，將數控機床運動速度控制為5m/min，采用所提方法、文獻[3]方法和文獻[4]方法展開螺旋旋轉體測試，對比上述方法的誤差補償精度，測試結果如圖4所示。

由圖4可知，文獻[3]方法和文獻[4]方法在螺旋旋轉體測試過程中獲得的曲線與理論曲線之間的偏差高于所提方法，因為所提方法補償數控機床的運動誤差之前，構建了多軸聯動的數控機床運動軌跡方程，根據軌跡方程計算多軸聯動數控機床的運動誤差，提高了誤差計算精度，進而提高了多軸聯動的誤差補償精度，可精準地完成螺旋旋轉體測試。

圖4 螺旋旋轉體測試

對比不同方法補償后在x軸、y軸中的運動誤差，測試結果如圖5所示。

由圖5可知，文獻[3]方法和文獻[4]方法的運動誤差隨著多軸聯動數控機床運動速度的提高不斷增大，表明以上兩種方法的運動誤差補償結果受數控機床運動速度影響較大，所提方法在x軸和y軸中的運動誤差均控制在±0.1mm以內，表明所提方法的運動誤差補償精度較高，且所提方法的運動誤差不隨著數控機床運動速度的提高而增大，表明所提方法的運動誤差補償結果不受多軸聯動數控機床運動速度的影響。

圖5 不同方法補償后的運動誤差

5 結束語

多軸聯動數控機床的機械轉動系統的固有頻率在機床高速運動過程中受到限制，導致機床出現運動誤差，為了提高多軸數控機床的加工精度，需要補償多軸聯動數控機床在運動過程中產生的誤差。目前數控機床運動誤差補償方法的誤差補償精度低且受機床運動速度的影響較大，提出多軸聯動的數控機床運動誤差補償方法，該方法根據機床運動軌跡方程計算運動誤差，采用優化后的PID控制器完成運動誤差補償，可有效完成橢圓控制和螺旋旋轉體控制，誤差補償結果不受機床運動速度的影響，為多軸聯動數控機床的應用與發展奠定了基礎。