基于Bayes的飲食裝備維修性驗(yàn)證與評(píng)估研究
寧初明,劉永新,沈燦鐸,李燕軍
(軍事科學(xué)院系統(tǒng)工程研究院軍需工程技術(shù)研究所,北京100010)
1 引言
飲食裝備的可維修性是裝備性能的重要組成部分,直接影響著裝備保障性能的有效發(fā)揮,對(duì)飲食裝備作業(yè)設(shè)備的可靠性及維修性進(jìn)行試驗(yàn)評(píng)估也是驗(yàn)收我軍升級(jí)改進(jìn)和新研飲食裝備的重要依據(jù)。在進(jìn)行飲食裝備維修性評(píng)估分析時(shí),由于飲食裝備總體規(guī)模偏小、故障和維修數(shù)據(jù)收集不成機(jī)制、維修性試驗(yàn)時(shí)間和經(jīng)濟(jì)成本過(guò)高等因素限制,飲食裝備的維修性數(shù)據(jù)量通常都難以達(dá)到GJB2072-94中不少于30樣本量的要求,維修性評(píng)估過(guò)程的小樣本數(shù)據(jù)問(wèn)題突出。因此,在保證維修性評(píng)估效果前提下,如何高效利用小量樣本數(shù)據(jù)進(jìn)行飲食裝備的維修性評(píng)估分析始終是飲食裝備維修性試驗(yàn)與評(píng)價(jià)研究的熱點(diǎn)話題。
基于Bayes理論的小子樣維修性驗(yàn)證經(jīng)過(guò)多年的發(fā)展,其已在裝甲裝備、航空裝備和艦艇導(dǎo)航裝備等領(lǐng)域已有較為廣泛的應(yīng)用[1-3]。本文通過(guò)借鑒Bayes小子樣理論和多源信息融合方法在導(dǎo)彈、裝甲裝備等領(lǐng)域的成功應(yīng)用經(jīng)驗(yàn)[4-6],提出了一種在小子樣條件下,基于Bayes理論和可信度加權(quán)的多源信息融合理論的飲食裝備維修性評(píng)估建模分析方法,這不僅能為我軍現(xiàn)有飲食裝備的科學(xué)維修提供技術(shù)支撐,對(duì)減少飲食裝備升級(jí)改造和研制過(guò)程中的試驗(yàn)次數(shù),縮短試驗(yàn)周期,降低試驗(yàn)成本等方面也具有重要軍事意義。
2 基于Bayes的小子樣維修性評(píng)估模型分析
2.1 維修時(shí)間分布模型的確定
維修時(shí)間的總體分布的確定是基于Bayes的小子樣維修性評(píng)估分析的基礎(chǔ)前提,通過(guò)對(duì)維修時(shí)間的分布擬合和模型檢驗(yàn)可確定維修時(shí)間的分布規(guī)律[7-9]。
1)維修時(shí)間分布模型擬合
維修時(shí)間分布模型的估計(jì)通常采用經(jīng)驗(yàn)分步法和直方圖法等方法來(lái)分析處理,而直方圖法一般適用于連續(xù)數(shù)據(jù)的分析,在基于Bayes的小子樣維修性評(píng)估分析中應(yīng)用較為廣泛。
假定維修時(shí)間為Y=[y1,y2,…yn],其概率密度為f,則采用直方圖法估計(jì)維修時(shí)間總體分布的過(guò)程如下:
①樣本分組數(shù)
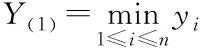
K=[1+3.32·ln(n)]
(1)
式中:[·]為向上取整。
②樣本區(qū)間分點(diǎn)和區(qū)間間隔
在區(qū)間[a,b)的維修時(shí)間的區(qū)間間隔Δ如式(2)所示。
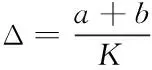
(2)
則區(qū)間[a,b)的各區(qū)間間隔分點(diǎn)如式(3)所示。
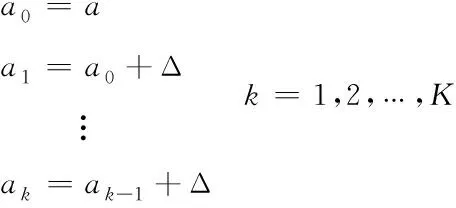
(3)
③樣本頻數(shù)和頻率
令樣本Y中數(shù)據(jù)在各小區(qū)間的個(gè)數(shù)為頻數(shù)ni(i=1,2,…,n),則各頻數(shù)對(duì)應(yīng)的頻率fi如式(4)所示。
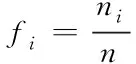
(4)
④維修時(shí)間分布直方圖
根據(jù)維修時(shí)間樣本Y的區(qū)間劃分和頻數(shù)情況,繪制維修時(shí)間的分布直方圖,并擬合出維修時(shí)間的近似概率密度曲線f(x)。
2)維修時(shí)間分布模型檢驗(yàn)
判斷維修時(shí)間總體分布模型后,需對(duì)分布模型進(jìn)行假設(shè)檢驗(yàn),通常采用適用于小樣本數(shù)據(jù)檢驗(yàn)的柯?tīng)柲缏宸驒z驗(yàn)法(K~S檢驗(yàn)法)。飲食裝備維修時(shí)間一般為對(duì)數(shù)正太分布,則可利用柯?tīng)柲缏宸驒z驗(yàn)法對(duì)維修時(shí)間分布模型進(jìn)行檢驗(yàn)。
對(duì)維修時(shí)間樣本Y取對(duì)數(shù)并從小大順序排序可得到新的維修時(shí)間樣本X=[x1,x2,…xn],則令樣本X總體分布服從正太分布N(μ,δ2)。
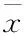
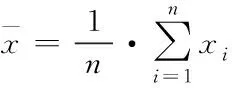
(5)
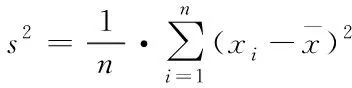
(6)
則樣本X的經(jīng)驗(yàn)分布函數(shù)Fn(x)如式(7)所示。
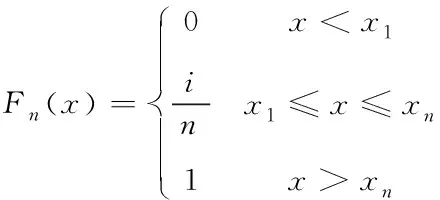
(7)
經(jīng)驗(yàn)分布函數(shù)Fn(x)與理論分布函數(shù)F(x)的最大偏差n如式(8)所示。
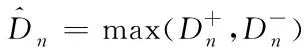
(8)
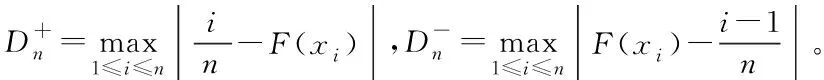
由給定的顯著性水平α查表可得臨界值nα,則對(duì)假設(shè)進(jìn)行檢驗(yàn):若n 由于樣本數(shù)據(jù)的小子樣特性,需確定樣本數(shù)據(jù)的驗(yàn)前分布密度。 1)單一信息源驗(yàn)前分布 采用精確度較高的隨機(jī)加權(quán)法來(lái)計(jì)算先驗(yàn)分布,其算法實(shí)現(xiàn)過(guò)程如下: (9) (10) (11) (12) (13) 2)基于可信度加權(quán)的多源信息融合 采用對(duì)服從對(duì)數(shù)正太分布的多源信息融合效果優(yōu)良且計(jì)算合理方便的基于可信度加權(quán)的融合理論來(lái)對(duì)飲食裝備的歷史維修時(shí)間數(shù)據(jù)和不同型號(hào)維修時(shí)間數(shù)據(jù)等多種信息源進(jìn)行加權(quán)融合得到信息源的驗(yàn)前分布[10-11],再經(jīng)Bayes理論修正后得到信息源的驗(yàn)后概率密度函數(shù)。 假設(shè)飲食裝備的初始信息源數(shù)量為m,采用信息源與中心數(shù)據(jù)的波動(dòng)程度Si作為多源信息融合的可信度權(quán)重引子,Si越小表明數(shù)據(jù)可信度越高,則Si可由式(14)和式(15)所示獲得 (14) (15) 對(duì)可信度權(quán)重引子進(jìn)行歸一化處理,第i個(gè)信息源權(quán)重wi為可由式(16)和式(17)所示獲得。 (16) (17) 則信息源融合后的驗(yàn)前密度π(θ)可由式(18)所示獲得 (18) 式中:θi為第i個(gè)信息源的分布參數(shù)。 通過(guò)現(xiàn)場(chǎng)試驗(yàn)得到試驗(yàn)樣本Θ=(θ1,θ2,…,θn),令f(θi|θ)為第i個(gè)試驗(yàn)信息的似然函數(shù),則可得如式(19)所示的試驗(yàn)樣本Θ的似然函數(shù) (19) 則由Bayes理論可得如式(20)所示的修正后的信息源驗(yàn)后概率密度函數(shù)π(θ|Θ) (20) 表1 維修性評(píng)估模型驗(yàn)證主要參數(shù) 作如式(21)的假設(shè) (21) 式中:θ0為合同給出的平均維修時(shí)間指標(biāo)值。 1)一致性檢驗(yàn) 假設(shè)的驗(yàn)前概率比如式(22)所示 (22) 由Bayes公式及式(22)可得如式(23)所示的假設(shè)的驗(yàn)后概率比為 (23) (24) 也即 (25) 當(dāng)式(24)成立時(shí),認(rèn)為平均維修時(shí)間MTTR符合要求,即接受原假設(shè),否則拒絕。 1)樣本量確定 (26) (27) 2)定義如式(28)和式(29)所示的類風(fēng)險(xiǎn)α、β。 (28) (29) P0、P1為H0、H1的驗(yàn)前概率密度,其表達(dá)式如式(28)和式(29)所示 (30) P1=1-P0 (31) 由式(28)和式(29)可得采用Bayes理論進(jìn)行維修性評(píng)估所需的最小試驗(yàn)樣本量如式(32)所示 (32) 式中:Z為標(biāo)準(zhǔn)正太分布的上分為點(diǎn)。 則采用Bayes理論和經(jīng)典方法進(jìn)行維修性評(píng)估所需的試驗(yàn)樣本關(guān)系如式(33)所示 (33) 由式(33)可知,采用Bayes理論的維修性評(píng)估可有效減小試驗(yàn)樣本量,這表明基于Bayes的小子樣維修性評(píng)估是可行的。 (34) (35) (36) 平均維修時(shí)間的均值和方差的Bayse估計(jì)[8]如式(37)和式(38)所示 Em(θ|X)(x)=μ1 (37) (38) 則均值θ在置信度為1-α?xí)r的區(qū)間估計(jì)[a,b]應(yīng)滿足式(39)的關(guān)系。 (39) 則均值θ的置信下界a和置信上界b應(yīng)滿足式(40)和式(41)的關(guān)系 (40) (41) 則均值θ的置信下界a和置信上界b分別如式(42)和式(43)所示 (42) (43) 則平均維修時(shí)間在置信度為1-α?xí)r的區(qū)間估計(jì)[Ta,Tb]的時(shí)間下界Ta和上界Tb分別如式(44)和式(45)所示 (44) (45) 以某型飲食裝備關(guān)鍵系統(tǒng)維修性為研究對(duì)象,其歷史平均維修時(shí)間數(shù)據(jù)TL、相似型號(hào)平均維修時(shí)間TX和現(xiàn)場(chǎng)試驗(yàn)數(shù)據(jù)TT分別如式(44)、式(45)和式(46)所示,維修性主要參數(shù)如表2所示 TL=[26,14,21,30,70,69,20,21,18,65,24](min) (46) TX=[16,35,26,16,40,28,42,33, (47) TT=[13,26,10,50,21,31,42,30,46](min) (48) 表2 飲食裝備維修性的主要參數(shù) 從圖1可初步認(rèn)為歷史平均維修時(shí)間服從對(duì)數(shù)正太分布,下面利用K~S檢驗(yàn)法對(duì)歷史平均維修時(shí)間分布模型進(jìn)行檢驗(yàn)。 圖1 歷史平均維修時(shí)間分布直方圖 將TL取對(duì)數(shù)并按從小到大排序可得樣本XL~N(μ,σ2),則K~S檢驗(yàn)的主要數(shù)值如表3所示。 表3 飲食裝備平均維修時(shí)間K~S檢驗(yàn) 對(duì)歷史平均維修時(shí)間和相似型號(hào)平均維修時(shí)間采用隨機(jī)加權(quán)法對(duì)其均值進(jìn)行3000次仿真分析,可得如圖2和圖3所示的仿真分布圖。 圖2 歷史數(shù)據(jù)驗(yàn)前分布仿真直方圖 則通過(guò)仿真擬合可得歷史平均維修時(shí)間和相似型號(hào)平均維修時(shí)間的驗(yàn)前分布分別如式(49)和式(50)所示。 圖3 相似型號(hào)數(shù)據(jù)驗(yàn)前分布仿真直方圖 π1(θ)~N(3.3735,0.57722) (49) π2(θ)~N(3.2592,0.46032) (50) 由式(15)可知兩組數(shù)據(jù)的可信度權(quán)重引子Si分別為S1=0.307、S2=0.1993,由式(17)可得其權(quán)重因子wi分別為w1=0.4785、w2=0.5215。則由式(18)可得融合后的驗(yàn)前如式(51)所示 π(θ)~N(3.313,0.13482) (51) 則維修性評(píng)估驗(yàn)證的判決規(guī)則為:若現(xiàn)場(chǎng)試驗(yàn)5次維修時(shí)間的對(duì)數(shù)均值滿足式(52) =4.4568 (52) 則認(rèn)為符合維修性要求,否則拒絕。 采用Bayes理論進(jìn)行平均維修時(shí)間評(píng)估所需的最小試驗(yàn)樣本量遠(yuǎn)小于GJB2072-94中30個(gè)以上樣本要求,因此可以說(shuō)基于Bayes理論的維修性評(píng)估可顯著減少所需試驗(yàn)樣本量。 (53) (54) 則由式(44)和式(45)可得在置信度為0.95時(shí)的平均維修時(shí)間區(qū)間估計(jì)的下界Ta和上界Tb分別如式(55)和式(56)所示 (55) (56) 同理可求得置信水平為0.90、0.80時(shí)平均維修時(shí)間的Bayes估計(jì),其具體計(jì)算結(jié)果如表4所示。由表4可知,現(xiàn)場(chǎng)試驗(yàn)樣本得到的平均維修時(shí)間點(diǎn)估計(jì)與合同給出的平均維修時(shí)間基本一致,這表明采用Bayes的平均維修時(shí)間估計(jì)方法是有效的,且隨著置信水平的下降,平均維修時(shí)間估計(jì)區(qū)間范圍也在縮小。因此,在飲食裝備維修性的置信水平確定后可求取平均維修時(shí)間估計(jì)區(qū)間,若現(xiàn)場(chǎng)維修時(shí)間在平均維修時(shí)間估計(jì)區(qū)間即可認(rèn)為飲食裝備的可維修性達(dá)到規(guī)定要求。 表4 平均維修時(shí)間的Bayes估計(jì) 本文以小子樣的飲食裝備維修性為研究對(duì)象,利用Bayes理論對(duì)飲食裝備維修性進(jìn)行了驗(yàn)證分析,并對(duì)不同置信水平下的平均維修時(shí)間進(jìn)行了評(píng)估分析。結(jié)果表明,采用Bayes理論的維修性評(píng)估可顯著減少所需試驗(yàn)樣本量,從而可有效降低試驗(yàn)次數(shù),縮短試驗(yàn)周期;利用Bayes方法進(jìn)行平均維修時(shí)間估計(jì)是可行的,且隨著置信水平的下降,平均維修時(shí)間估計(jì)區(qū)間范圍也在縮小。2.2 基于可信度加權(quán)的多源驗(yàn)前分布確定
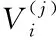
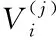
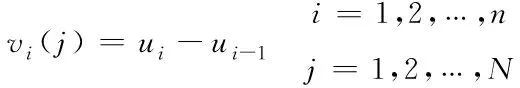
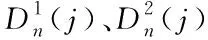
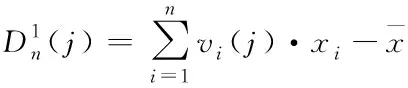
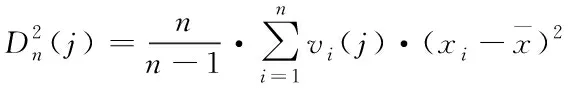
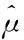
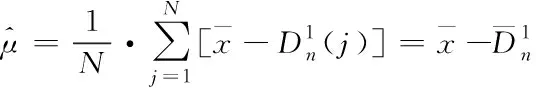
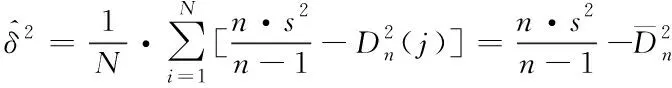
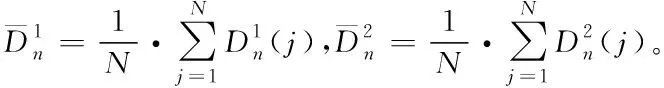
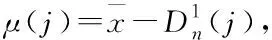
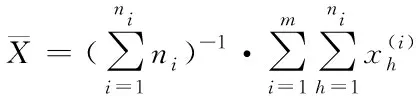
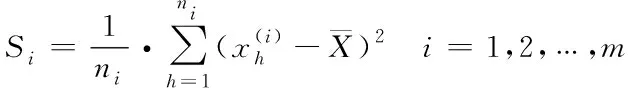
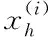
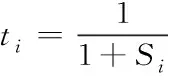
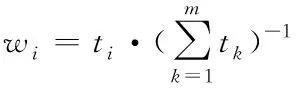
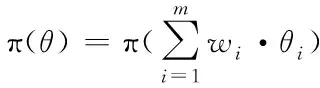
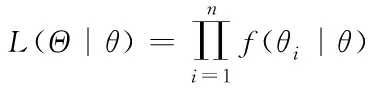
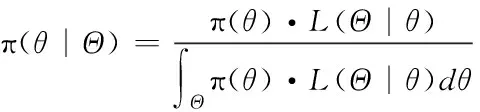
2.3 基于Bayes的維修性評(píng)估模型驗(yàn)證
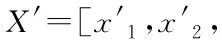
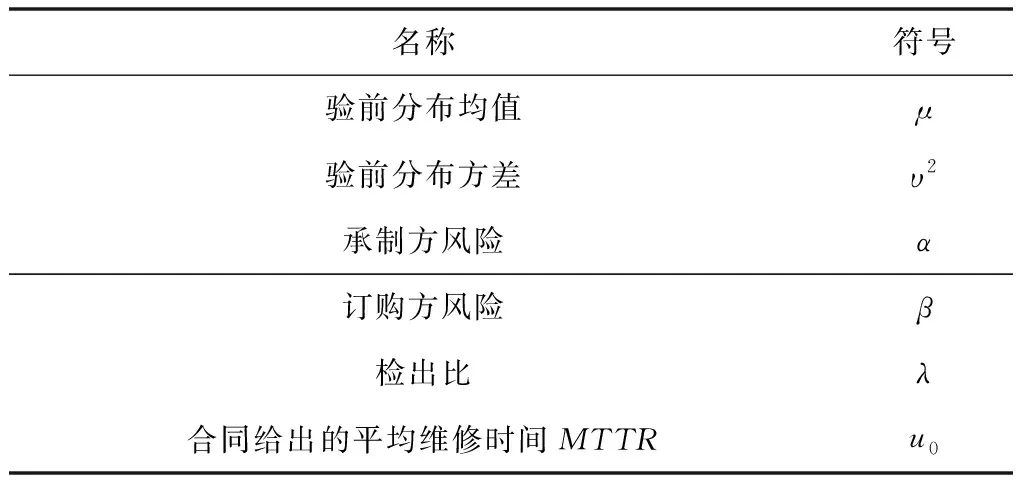
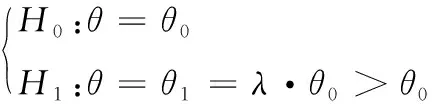
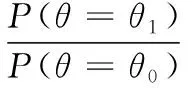
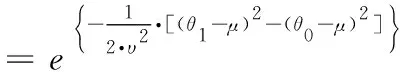
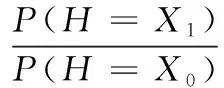
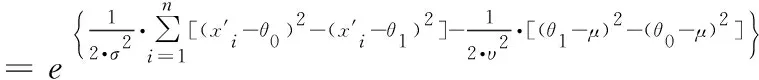
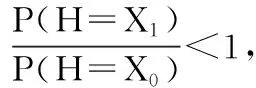
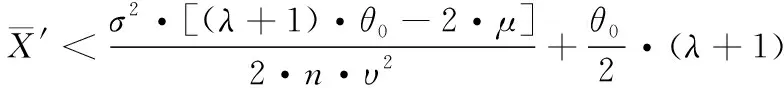
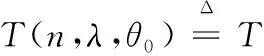
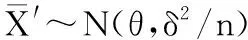
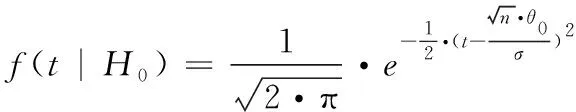
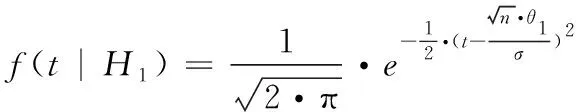
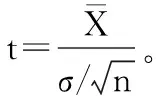
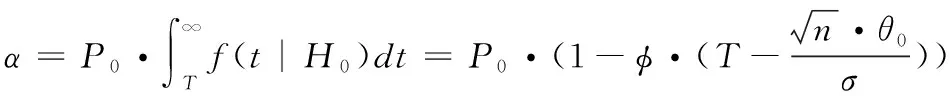
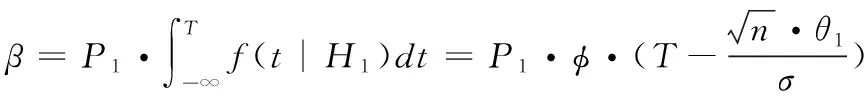
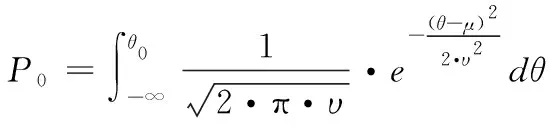
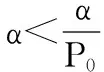
3 基于Bayes的平均維修時(shí)間估計(jì)
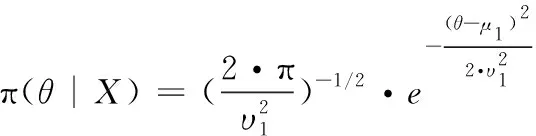
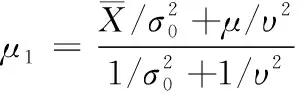
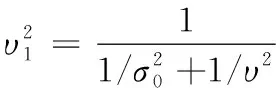
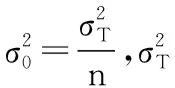
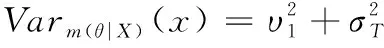
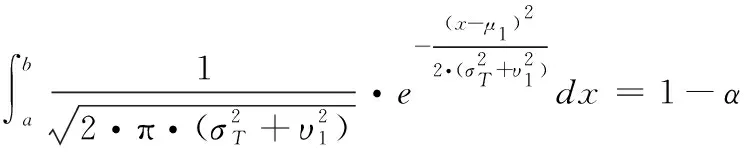
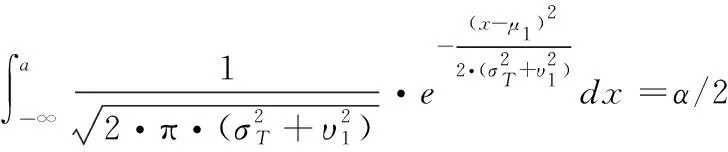
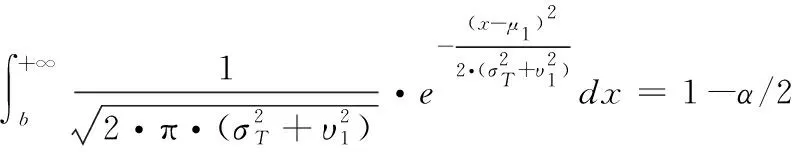
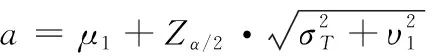
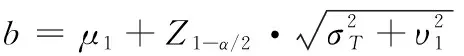
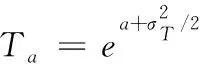
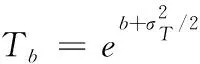
4 飲食裝備維修性驗(yàn)證與評(píng)估分析
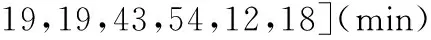

4.1 平均維修時(shí)間總體分布

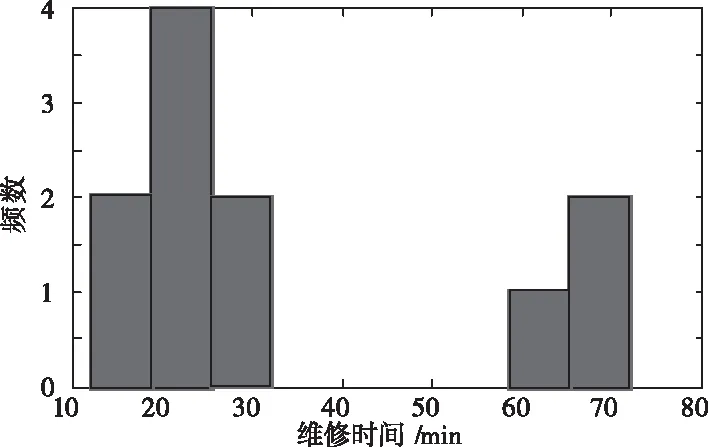
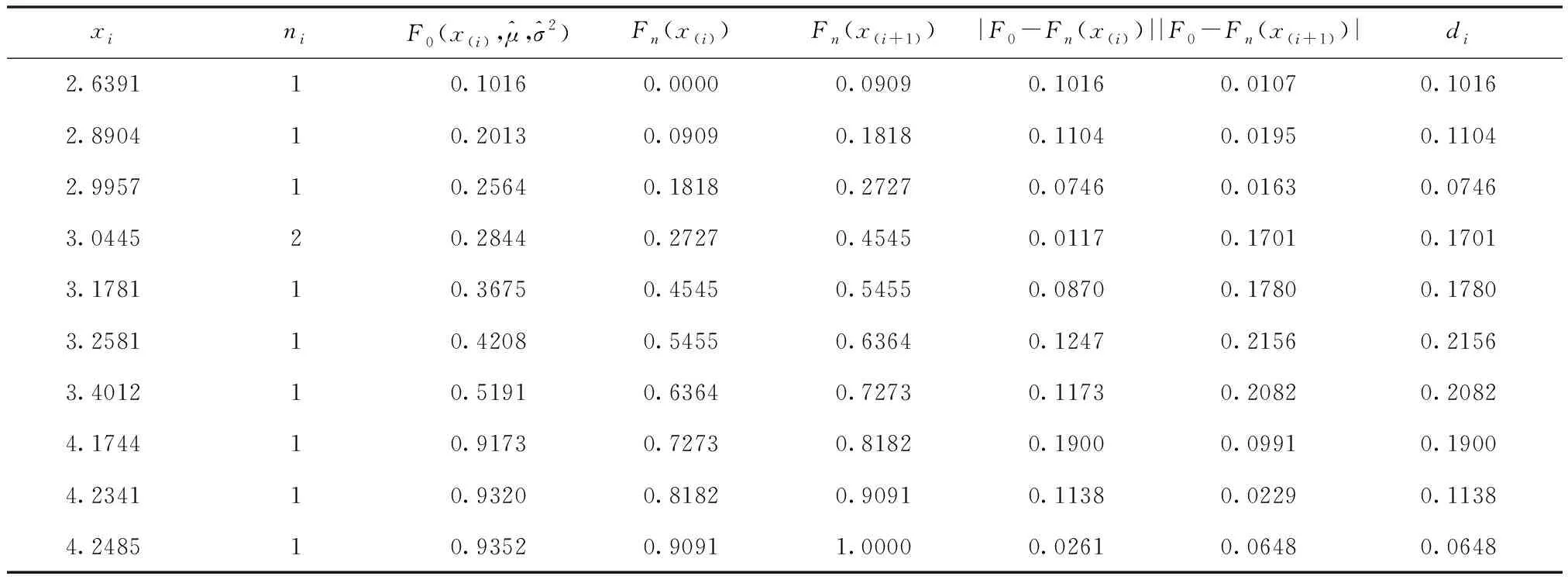
4.2 多源信息融合的驗(yàn)前分布確定
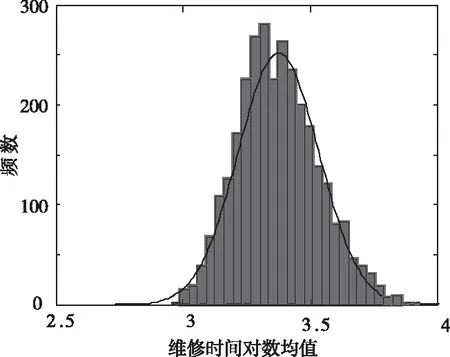
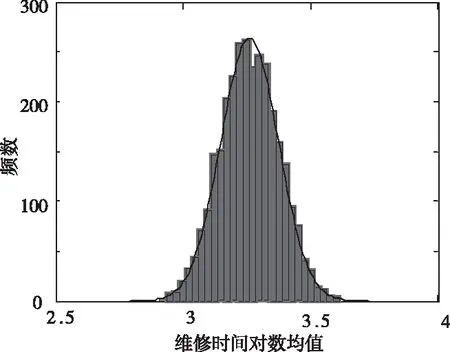
4.3 基于Bayes的平均維修時(shí)間評(píng)估模型驗(yàn)證
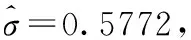
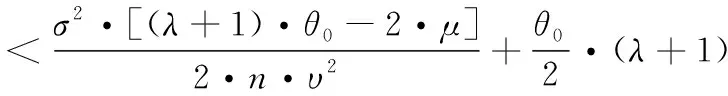
4.4 基于Bayes的平均維修時(shí)間估計(jì)
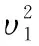
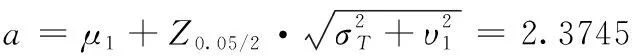
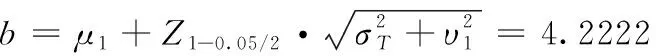
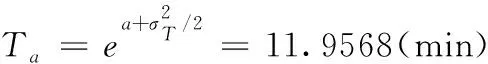
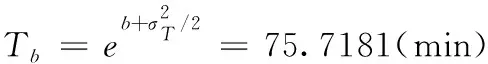

5 結(jié)語(yǔ)

