船載高頻地波雷達一階海雜波仿真模型研究

韓文強，李慶忠

(中國海洋大學(xué)工程學(xué)院，山東 青島 266100)

1 引言

高頻地波雷達(High Frequency Surface Wave Radar，HFSWR)根據(jù)雷達平臺的安裝方式可以分為岸基HFSWR和船載HFSWR，岸基HFSWR具備實時、探測距離遠、覆蓋面積廣及全天候等優(yōu)點，但是岸基HFSWR的監(jiān)測僅限于沿海海域[1]。船載HFSWR除了以上優(yōu)點之外，還具備很強的靈活機動性，進一步擴大了雷達的探測范圍，提高了監(jiān)測的穩(wěn)定性，廣泛用于監(jiān)測開放海域的艦船目標。

對于船載HFSWR，由于海浪與平臺運動的相互的作用，海洋回波特性相對于岸基HFSWR更加復(fù)雜，前向運動會引起回波多普勒譜中的一階海雜波展寬，導(dǎo)致展寬域中的目標被掩蓋[2]，這對位于展寬域中的低速小目標檢測非常不利。

長期以來，如何抑制海雜波都是學(xué)者研究的重點，但是由于實測數(shù)據(jù)不足以及影響因素未知性較大，導(dǎo)致海雜波抑制算法的研究難以有很好的實驗數(shù)據(jù)支撐。因此，亟需進行海雜波模型的仿真研究，為后期海雜波抑制與目標檢測算法研究提供依據(jù)，并能有效評估雷達在雜波環(huán)境中的工作性能。

目前，常見的海雜波建模方法主要有以下三種：基于統(tǒng)計模型的海雜波建模、基于雷達截面散射機理的海雜波模型和基于空時分析的海雜波建模。

基于統(tǒng)計模型的海雜波建模方法描述的是海雜波在時域幅度上的變化，其核心思想是將海雜波看成是來自雷達照射區(qū)域分辨單元內(nèi)多個散射體后向散射矢量的疊加。典型的分布模型包括：Weibull分布、K分布、對數(shù)-正態(tài)分布、Pareto分布和Tsallis分布等[3-5]，這些統(tǒng)計分布模型只能適合某些特定的海洋環(huán)境，具有較大的局限性[6]。

基于雷達截面散射機理的海雜波模型就是利用海面電磁散射機理，從而建立合適的電磁波與散射介質(zhì)之間的相互作用模型，最后通過建立雷達散射截面方程的來實現(xiàn)海雜波的建模。如Khoury等人[7]從雷達回波信號的角度對浮動平臺下的雷達截面積以及海雜波多普勒譜進行了分析，同時研究了風(fēng)速和風(fēng)向?qū)M蕩和縱蕩運動的影響；馬嬌[8]由一階電場方程推導(dǎo)出了海雜波的一階雷達截面方程，并得到了回波信號的表達式；Sun等人[9]推導(dǎo)了具有橫蕩運動和前向運動的船載HFSWR的反射截面模型；另外賀超[10]和周企豪[11]也都在自己的研究中用到了基于雷達截面散射機理的海雜波模型。

實際的雷達回波數(shù)據(jù)一般是三維數(shù)據(jù)，即距離、多普勒維和方位維，因此空時建模也是海雜波建模的常見方式。如Sun等人[2][9][12]在實驗中發(fā)現(xiàn)船載平臺的運動會導(dǎo)致一階海雜波譜展寬，除此之外還提出了本征譜結(jié)構(gòu)和時空分布模型。Cai等人[13]分析了縱蕩運動或橫蕩運動對船載HFSWR一階海雜波時空分布的影響。Yao等人[14]分別對六自由度和前向運動對一階海雜波時空分布的影響進行了分析，發(fā)現(xiàn)多自由度運動產(chǎn)生的附加峰也會被展寬的一階海雜波覆蓋。空時分析的建模可以很好的建立全維度的海雜波仿真模型，針對不同的平臺使用不同的波段，具有很好的推廣性。

但目前基于空時分析的海雜波建模方法[12-14]都只考慮了船載平臺前向運動會引起一階海雜波的展寬問題，并沒有考慮相參積累時間內(nèi)艦船前向運動會造成不同距離元上的一階海雜波分布特性的不均勻性，故構(gòu)建的海雜波仿真數(shù)據(jù)和實測的海雜波數(shù)據(jù)存在較大的差異，不利于后續(xù)海雜波有效抑制方法的研究。

為克服目前以上基于空時分析的海雜波建模方法存在的問題，本文對船載HFSWR一階海雜波空時分布特性進行了研究，理論分析了船載平臺前向運動時回波方位角改變對時空分布模型的影響，在考慮前向運動和艦船平臺三自由度擺動因素下，建立了一階海雜波時空分布的改進模型，再通過引入海雜波在傳播過程中距離衰減模型，便可得到三維的海雜波仿真數(shù)據(jù)。最后，根據(jù)改進的空時分布模型還建立了基于SwerlingIV的艦船目標模型。仿真驗證了提出改進模型的有效性和可行性。

2 船載HFSWR海雜波特性分析及建模

2.1 一階海雜波空時分布模型

對于岸基HFSWR，根據(jù)Bragg散射原理，當(dāng)海浪波長為雷達波長一半時，會產(chǎn)生關(guān)于多普勒頻率對稱的正負一階Bragg峰[2][9][12-14]。基于單基地雷達多普勒公式，一階Bragg頻率公式如下

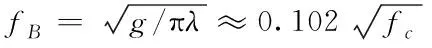
(1)

其中g(shù)=9.8m/s2為重力加速度；λ為雷達波長，單位為m；fc=c/λ為雷達載波頻率，單位為MHz，c為光速。

而對于船載HFSWR，為了準確建立船載海雜波的空時分布模型，本文首先對船載平臺只有前向運動條件下的海雜波幾何模型進行分析。圖1顯示的是船載HFSWR某個距離元r上一個海雜波子塊P1的幾何模型。假設(shè)船載平臺前向運動速度為Vp，對于雜波子塊P1，傳統(tǒng)的海雜波空時分布模型為

fd=fdpcosφ0±fB

(2)

其中fdp=2Vp/λ為雷達平臺運動引起的多普勒頻率。因此傳統(tǒng)模型中當(dāng)只考慮平臺前向運動時，平臺的前向運動會給不同方向的海雜波引入額外的多普勒頻率，導(dǎo)致一階海雜波多普勒域展寬[15-17]。但是該模型中雜波塊P1相對于觀測點A的入射方向與平臺速度方向的夾角φ0在整個相參積累周期內(nèi)是固定不變的，這就是傳統(tǒng)模型的存在的嚴重缺陷。因為，一個相參積累周期通常為數(shù)分鐘，在這段測量時間內(nèi)，船載移動平臺會產(chǎn)生一定的平移位移量。下面具體分析在一個相參積累周期內(nèi)，夾角φ0的變化規(guī)律。

如圖1所示，在某個相參積累時間t內(nèi)，船載平臺從觀測點A(某個陣元)以前向速度Vp運動到觀測點B，則觀測點A與B之間的距離為Vpt。當(dāng)相參積累開始時，雜波塊P1相對于觀測點A的入射方向與平臺速度方向的夾角為φ0(0)=φ0，而在相參積累時間t時，船載平臺觀測移動到了觀測點B，此時雜波塊P1入射方向與平臺速度方向夾角變?yōu)棣?(t)。可見，在一個相參積累周期內(nèi)，對同一海雜波子塊，相對于某一陣元的觀測角是變化的。根據(jù)三角函數(shù)定理，由圖1可知

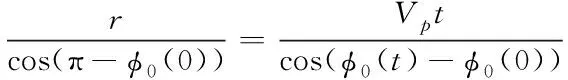
(3)

化簡后得

φ0(t)=arctan(cot(φ0)+(Vptsec(φ0))/r)

(4)

因此，在一個相參積累周期內(nèi)，雜波子塊與觀測陣元的入射夾角是一個隨著時間變化的函數(shù)。由此推得船載平臺只有前向運動條件下，改進的海雜波空時分布模型為

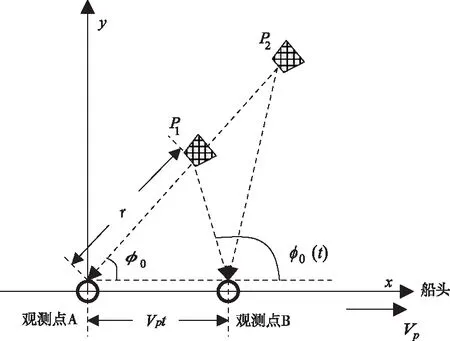
圖1 船載HFSWR海雜波幾何模型

fd=fdpcosφ0(t)±fB

=fdpcos[arctan(cot(φ0)+(Vptsec(φ0))/r)]±fB

(5)

此改進模型與傳統(tǒng)模型(2)相比，主要具有兩個不同點：一是在同一距離元內(nèi)，海雜波接收信號的角度會隨著相參積累時間的變化而變化；二是對于不同距離元，由圖1可知，不同距離元但是回波入射角相同的雜波塊P1與P2，在一個相參積累周期內(nèi)，兩者的回波入射角度隨時間變化的函數(shù)是不一致的。這就說明在一個相參積累周期內(nèi)，隨著船載平臺的運動，不同距離元的海雜波回波信號在距離尺度上的分布特性是不一致的，這從理論上解釋了為什么實測海雜波數(shù)據(jù)在不同距離元上并不服從獨立同分布的假設(shè)。

在以上一階海雜波時空分分析的基礎(chǔ)上，下面建立艦船復(fù)雜運動模式下一階海雜波時空分布模型。一般情況下，船載平臺除了前向運動外，還包括海浪或風(fēng)浪引起的六自由度運動，具體如圖2所示。包括沿三坐標軸方向的三自由度平動(縱蕩、橫蕩、垂蕩)；以及繞三坐標軸方向的三自由度擺動(橫搖、縱搖、艏搖)。實測實驗表明[16]，三自由度平動對一階海雜波的空時分布影響很小，可忽略不計，故本文只考慮三自由度擺動對船載平臺的影響，即只考慮側(cè)傾運動φ(t)、俯仰運動ψ(t)、以及偏航運動φ(t)(如圖2所示)在海雜波子塊回波方向引起的附加多普勒頻移[9][16][17]。

在三自由度擺動影響下，船載雷達平臺水平面上的速度向量組成如圖3所示。其中d為陣元間距，接收陣元數(shù)目為N，不考慮雷達偏航時候，海雜波回波子塊至雷達陣元的入射方向與平臺前向運動速度方的夾角為φ0(t)。圖中Vs為雷達平臺某陣元與海雜波子塊對應(yīng)的徑向速度，Vroll是由側(cè)傾引起的速度，Vroll=h0d[φ(t)]/dt，h0是天線陣元的高度，Vpcos[ψ(t)]和Vrollcos[φ(t)]分別是Vp和Vroll在水平面的x軸和y軸上的投影。

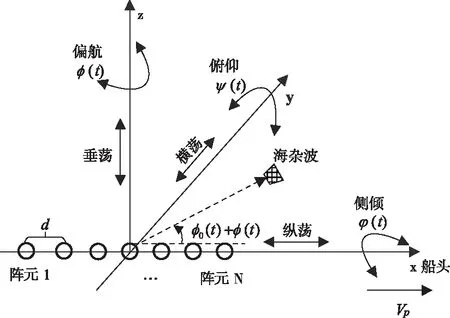
圖2 船載平臺六自由度示意圖

由于一階海雜波時空分布模型的構(gòu)成包括：除了一階Bragg頻移fB外，還需要考慮船載平臺在以上三個擺動和一個前向運動造成的在接收方向的附加多普勒頻移。因此在考慮φ0(t)的變化和以上運動影響下，推得的艦船復(fù)雜運動模式下一階海雜波時空分布模型如下

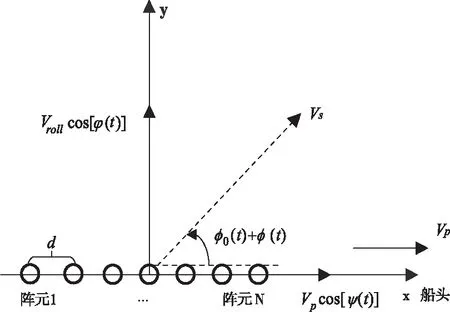
圖3 三自由度擺動影響下水平面速度向量

fd=fdp(t，φ0(t))±fB

(6)

fdp(t，φ0(t))=2Vs/λ

(7)

Vs=Vpcos[ψ(t)]cos[φ0(t)+φ(t)]+

Vrollcos[φ(t)]sin[φ0(t)+φ(t)]

(8)

因為艦船在波浪擾動的作用下，3自由度擺動具有一定的周期形式，故本文以正弦變化的周期振蕩函數(shù)來描述三個擺動運動

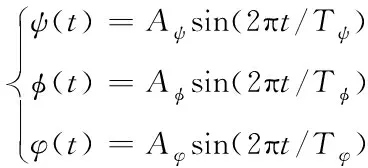
(9)

其中Aψ為俯仰角幅度，Aφ為偏航角幅度，Aφ為側(cè)傾角幅度，單位均為rad；Tψ為俯仰周期，Tφ為偏航周期，Tφ為俯仰周期，單位均為s。

值得注意的是，式(5)和(6)中的φ0(t)是隨時間變化的，而目前傳統(tǒng)模型中該夾角是保持固定不變的，φ0(t)的具體計算見式(4)。該模型與傳統(tǒng)模型相比，同樣具有兩個不同的特點：一是在同一距離元內(nèi)，海雜波接收信號的波達角會隨著相參積累時間的變化而變化；二是不同距離元的海雜波回波信號在距離尺度上的分布特性是不一致的。

2.2 海雜波回波信號模型

船載HFSWR的測量范圍通常在150km左右，理論上所有的距離單元均有海雜波分布，且對于廣闊的海平面而言，所有方向都可能存在海浪回波，故所有角度單元上同樣都存在海雜波。可以把每個角度-多普勒-距離單元中的海雜波當(dāng)成一個點目標，故該距離元的海雜波回波信號可以看作該距離元對應(yīng)半圓環(huán)內(nèi)不同方向獨立雜波塊回波信號的累加[16][17]，各距離元半圓環(huán)的構(gòu)成以及雜波子塊的示意如圖4所示。

下面建立船載HFSWR在前向運動和三自由度擺動下的海雜波回波信號模型。在考慮船載平臺前向運動對一階海雜波回波入射角影響的情況下，對于某個陣元，距離元r內(nèi)波達角為φ0(t)的雜波塊，其回波信號的時域模型為

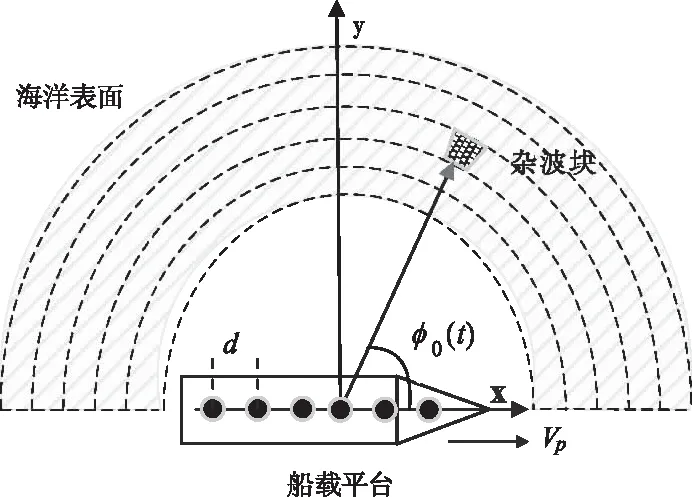
圖4 各距離元海雜波構(gòu)成示意圖

st(t)=At(ej2πfd1t+ej2πfd2t)

(10)

其中At為幅值，服從瑞利分布；fd1與fd2分別為海浪靠近雷達和遠離雷達的多普勒頻率，本文由前面推導(dǎo)的式(3)-(6)計算，其中

(11)

其中回波入射角φ0(t)是隨著時間變化的，但是半圓環(huán)內(nèi)所有角度對應(yīng)的雜波子塊回波信號的累加就是相對某個雷達陣元該距離元r的總的回波信號，如下式

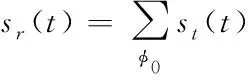
(12)

其中φ0∈[0°，180°]。

對于所有陣元，一個距離元接收到的所有數(shù)據(jù)叫一個快拍數(shù)據(jù)，根據(jù)空間導(dǎo)向矢量即可得出。在三自由度擺動下，由所有陣元之間的相位差組成的空間導(dǎo)向矢量為：

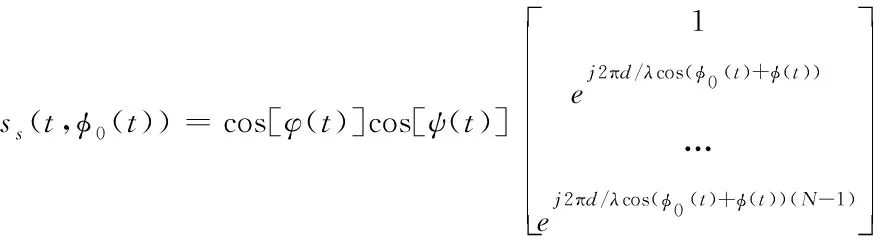
(13)

式中N是陣元數(shù)目。由此得到的一個快拍數(shù)據(jù)模型如式(14)所示

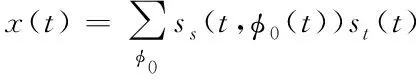
(14)

雖然式(14)在形式上和文獻[14-16]類似，但本文模型中，φ0(t)是隨時間變化的，而文獻[14-16]的模型中該夾角是保持固定不變的，故后續(xù)仿真有較大區(qū)別。

由于高頻地波雷達的發(fā)射及接收信號采用線性調(diào)頻連續(xù)波(Frequency Modulated Continuous Wave，F(xiàn)MCW)的形式[17]，在一個脈沖積累時間內(nèi)，發(fā)射M個脈沖，脈沖重復(fù)周期為Tr，不同時刻時間變化規(guī)律為t∈[0，Tr，2Tr，…，(M-1)Tr]，因此對于某個距離元，所有陣元在整個脈沖積累過程中所接收到的信號數(shù)據(jù)為一個N×M維的二維快拍數(shù)據(jù)X，如式(15)所示

X=[x(0)，x(Tr)，…，x((M-1)Tr)]

(15)

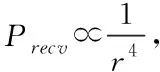
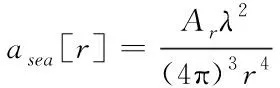
(16)

其中Ar為衰減系數(shù)，λ為雷達發(fā)射波波長。

通過式(15)推導(dǎo)的某一距離元一階海雜波的二維數(shù)據(jù)，以及式(16)距離衰減向量，可由下式構(gòu)建N×M×rmax的三維一階海雜波數(shù)據(jù)

Dsea(r)=asea[r](X+Noise)

(17)

其中Dsea為N×M×rmax的三維數(shù)據(jù)；rmax為雷達探測最遠距離；r表示距離索引；Noise表示高斯白噪聲。值得注意的是，因為式(17)是在式(5)和(8)的基礎(chǔ)上推導(dǎo)而來，由于不同距離元各雜波子塊的回波入射角度隨時間變化的規(guī)律是不一致的，所以根據(jù)式(17)產(chǎn)生的海雜波三維數(shù)據(jù)，在一個相參積累周期內(nèi)，不同距離元的海雜波回波信號在距離尺度上的分布特性是不一致的，這是本文海雜波回波信號的特點之一。

2.3 目標回波模型

在實際雷達接收的回波信號中，除了包含一階海雜波外，還包含艦船目標等。仿真目標一般作勻速直線運動，在低海態(tài)下可以不考慮目標三自由度擺動對目標速度的影響，即仿真目標可以看出一個點目標。仿真目標的速度向量如圖5所示，圖中Vt是所加入船目標的速度，Vtr是船目標的徑向速度，φ0t(t)為某一時刻目標回波入射方向與船載平臺前向運動速度方向夾角。對于船載HFSWR，仿真目標和一階海雜波子塊的模型類似，可以看作是海平面上獨立的一塊，隨著船載平臺的運動，φ0t(t)也是一個隨時間變化的函數(shù)，而非像傳統(tǒng)目標模型[10][16]一樣，φ0t(t)固定不變。

在一個相參積累周期內(nèi)的t時刻，所有陣元接收到的目標回波信號時域數(shù)據(jù)模型xt(t)為

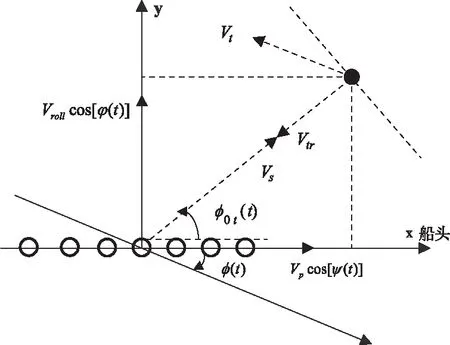
圖5 仿真目標速度向量

xt(t)=sst(t，φ0t(t))ej2πf0tt

(18)

其中f0t是目標相對某陣元的徑向多普勒頻移，見式(19)，式中的fdp為平臺前向運動引起的額外的多普勒頻移，公式中的第二部分是目標徑向速度引起的多普勒頻移。

f0t=fdp(φ0t(t)，t)+2Vtr/λ

(19)

ss(t，φ0t(t))為空間導(dǎo)向矢量

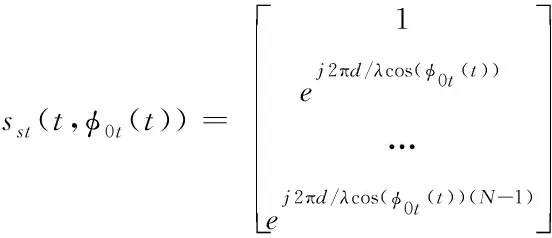
(20)

因此在一個相參積累周期內(nèi)，所有陣元所接收到的仿真目標空時數(shù)據(jù)Xt如下

Xt=[xt(0)，xt(Tr)，…，xt((M-1)Tr)]

(21)

由于雷達探測目標具有各種各樣的形狀與散射特征，在一個雷達分辨單元內(nèi)，目標回波散射通常由多個散射單元構(gòu)成，難以用一個精簡的模型加以限定，因此對于目標回波散射回波幅值強度一般采用統(tǒng)計模型[10][16]。由于船載平臺運動，目標回波入射角也是一個隨著時間變化的函數(shù)，因此本文選用最為經(jīng)典的SwerlingIV幅度起伏模型，該模型比較適合大的反射體在方位上有小變化的目標[19]。另外通過仿真目標不同距離上的相位關(guān)系，將二維仿真目標擴展至三維，可以得到如下三維目標數(shù)據(jù)Dt(r)

Dt(r)=at[r](SerlingIV(ps)⊙Xt)

(22)

其中⊙為Hadamard積，表示空時數(shù)據(jù)Xt的每一項都乘上一個常數(shù)；ps表示仿真船目標的平均幅度，由目標所在距離元空時數(shù)據(jù)取平均所得

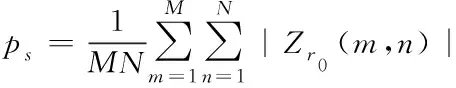
(23)

at為船目標復(fù)幅度向量，通過目標在距離維上的相位關(guān)系進行傅里葉變換所得

at=FT(ph⊙hr)

(24)

其中FT表示傅里葉變換；hr表示長度為rmax×1的漢寧窗口；ph為仿真目標在距離維上的相位信息

ph=[1，ej2πr0/rmax，…，ej2πr0(rmax-1)/rmax]

(25)

式中r0表示仿真目標所在距離單元；rmax表示雷達最大探測距離。

3 仿真結(jié)果分析

本節(jié)根據(jù)以上提出的海雜波模型對海雜波三維數(shù)據(jù)進行仿真，并與實測海雜波數(shù)據(jù)進行對比，從而驗證提出模型的有效性。表1給出的是仿真模型所用到的參數(shù)，表2給出的是三自由度擺動運動的相關(guān)參數(shù)。為了更好的對海雜波進行仿真，本文在仿真模型中加入了20dB的高斯白噪聲。

表1 模型參數(shù)列表

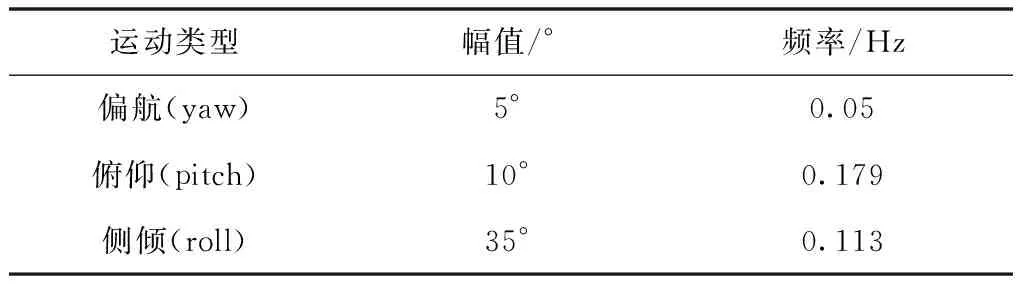
表2 三自由度擺動參數(shù)

3.1 同一距離元一階海雜波仿真結(jié)果與分析

首先根據(jù)表2中的三自由度擺動運動參數(shù)，考察船載平臺以不同前向速度運動時，同一距離元一階海雜波分布特性的變化規(guī)律。圖6顯示的是當(dāng)船速分別為0 m/s、1 m/s、3 m/s和5 m/s時，50 km處某一距離元的多普勒頻譜曲線。

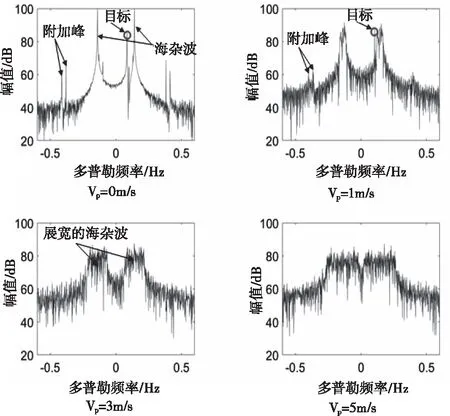
圖6 同一距離元不同速度下的一階海雜波多普勒譜曲線

圖7顯示的三自由度擺動運動下，50 km處不同前向速度運動下一階海雜波角度-多普勒譜(AD譜)。圖7中，仿真目標添加在該距離元方位角為60°的位置，其余弦值為0.5，故在圖中在方位余弦為0.5處能量幅值最大。由圖可見，當(dāng)船載平臺速度為0時，在AD譜中目標、一階海雜波和附加峰都是一定多普勒頻率的豎線。當(dāng)船載平臺前向速度增加后，一階海雜波會在多普勒域中展寬，展寬的海雜波會逐漸把目標覆蓋。此外，由三自由度擺動引起的附加峰也會因船載平臺的運動而展寬，并逐漸被展寬的一階海雜波覆蓋。當(dāng)船載平臺速度很大時，會出現(xiàn)正負一階海雜波重疊的情形，對目標的檢測更加不利。

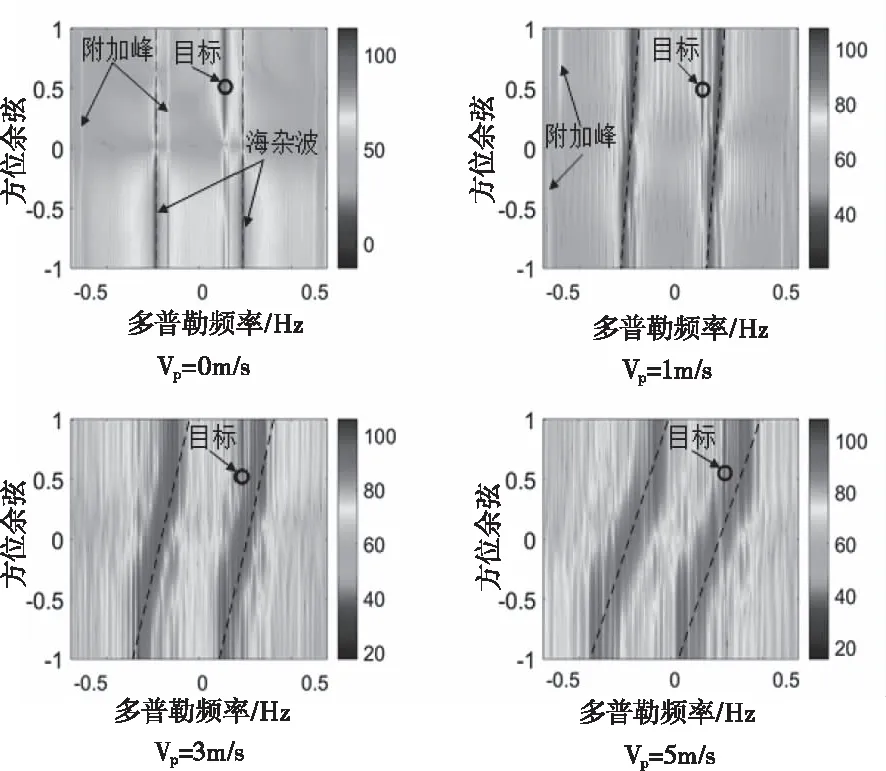
圖7 一階海雜波AD譜

3.2 不同距離元一階海雜波仿真結(jié)果與分析

為了分析平臺三自由度運動和前向運動對一階海雜波在距離維度上分布特性，圖8顯示的是一階海雜波距離-多普勒譜(RD譜)。本文將目標添加在50 km的位置，當(dāng)速度為0 m/s時，目標在RD譜中為一個具有一定能量的點，目標在RD譜中為一個具有一定能量的點，但是很可能被附近的附加峰或一階海雜波覆蓋，這對目標檢測造成困難。隨著速度增加，一階海雜波逐漸展寬，目標被高能量的一階海雜波覆蓋，同時附加峰也淹沒在一階海雜波之中。

除此之外，當(dāng)速度為0m/s時，一階海雜波在不同距離元上都表現(xiàn)為均勻的同分布，只是表現(xiàn)出一定的幅值衰減。但是隨著船載平臺運動速度增加，如圖8船載平臺速度Vp=3m/s時，區(qū)域1和區(qū)域2在不同的距離元，除了有幅值上的衰減以外，不同距離元還表現(xiàn)出不同的分布特性，并不服從均勻同分布。這種差異會導(dǎo)致協(xié)方差矩陣估計不準確，為后續(xù)海雜波抑制算法的研究造成困難[19]。主要原因是由于船載平臺運動時，實際觀測點的雜波塊的角度和源點處的角度是不一樣的，這導(dǎo)致在不同距離上的海雜波會有不同的分布，以上結(jié)果分析與1.3節(jié)理論分析一致。

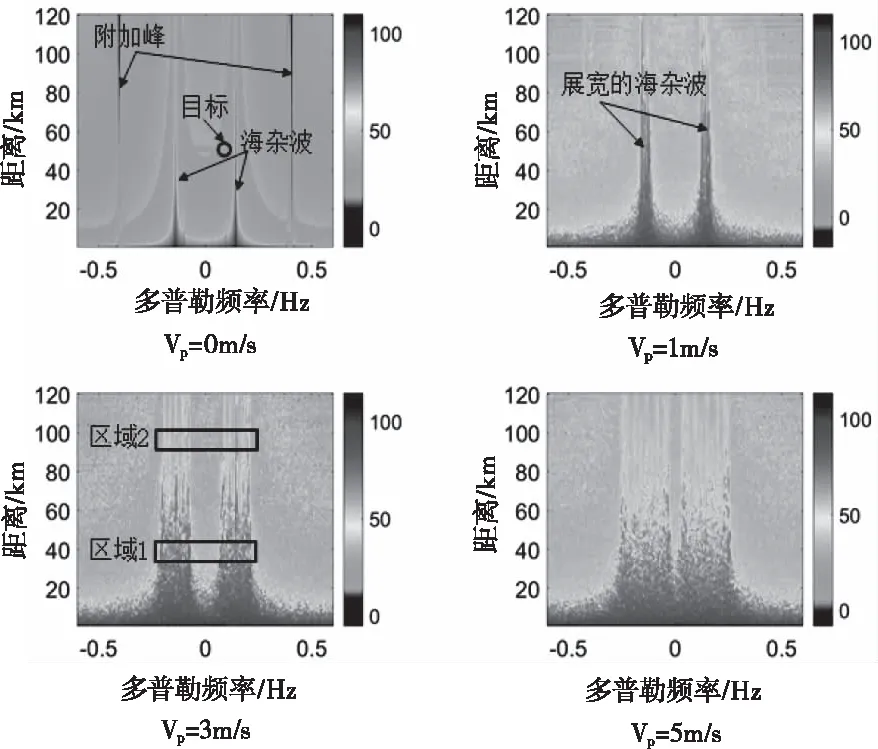
圖8 一階海雜波RD譜

3.3 一階海雜波仿真結(jié)果對比

為進一步說明本文提出的改進海雜波模型的有效性，分別于傳統(tǒng)模型仿真結(jié)果和實測海雜波實驗結(jié)果進行了對比，本文實測實驗結(jié)果來自于威海移動站2019年7月20日7時51分測得的數(shù)據(jù)，傳統(tǒng)模型和改進模型仿真雷達參數(shù)如表1所示都與實驗雷達參數(shù)一致。其中在傳統(tǒng)船載海雜波時空分布模型[16][17]中，在一個相參積累周期(約2.5分鐘左右)內(nèi)，海雜波子塊的回波入射角度是不變的，且假設(shè)不同距離元的海雜波分布具有獨立同分布特性。圖9顯示的是船載平臺在三自由度擺動下，艦船前向速度為5m/s時三種方法的RD譜對比，和一個距離元截面的多普勒譜曲線對比。

由于實測數(shù)據(jù)受到電離層雜波的干擾影響較大，仿真數(shù)據(jù)不考慮電離層雜波，本文僅拿圖9中方框區(qū)域作對比，由圖9(a)可見，傳統(tǒng)模型的海雜波RD譜圖，除了在距離維呈現(xiàn)幅值衰減外，海雜波在距離維上呈現(xiàn)出基本一致的分布特性。而由圖9(c)可見，實際的海雜波RD譜圖上，除了電離層雜波和地雜波之外，不同距離元上的一階海雜波其分布特性出現(xiàn)較大不一致性。由圖9(b)可知，本文改進模型生成的海雜波RD譜圖，在距離維上也呈現(xiàn)出分布特性的不一致性，這與實際船載海雜波分布特性更為接近。另外，如三種模型的多普勒截面，本文因考慮了船載平臺運動引起海雜波回波入射角改變的因素，所得的一階海雜波多普勒曲線的分布特性很不均勻，這與圖(c)實際的一階海雜波多普勒曲線更加接近。然而傳統(tǒng)模型中雖然加入了高斯白噪聲，但是其仍然無法模擬出實測海雜波的不均勻特性。

為了更好地展示本文模型和傳統(tǒng)模型在不同距離元上分布特性的差異，圖10顯示的分別50 km和110 km處兩個距離元的多普勒截面曲線。圖10(a)為傳統(tǒng)模型兩個距離元上的多普勒截面，圖10(b)為改進模型兩個距離元上的多普勒截面曲線。易于發(fā)現(xiàn)，本文改進模型在不同距離元上除了有明顯的幅值衰減外，在不同距離元上的分布特性也是不一樣的。而傳統(tǒng)模型在不同距離元上的分別形狀特性是完全一致的，僅在幅值上出現(xiàn)衰減。

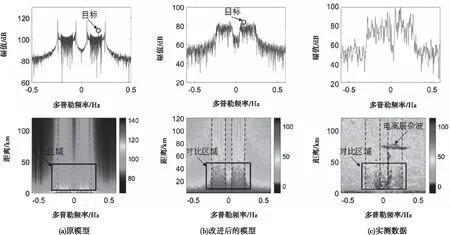
圖9 仿真模型對比

如圖11所示的是三自由度擺動影響下，目標位于50 km處，艦船前向速度為5m/s時三種方法的AD譜對比。由圖11(a)所示，傳統(tǒng)的一階海雜波AD譜在一階海雜波展寬的邊緣幅值都非常高，但是如圖(c)所示，實際上不同多普勒頻率的海雜波分布是非常不均勻的，展寬邊緣處的幅值不是最大的。由圖(b)可見，本文改進的模型在展寬邊緣處的幅值不是最大的，另外不同多普勒頻率上的海雜波幅值變化也是非常不均勻的。從AD譜中可以看出本文改進模型的AD譜更接近實際數(shù)據(jù)的AD譜。

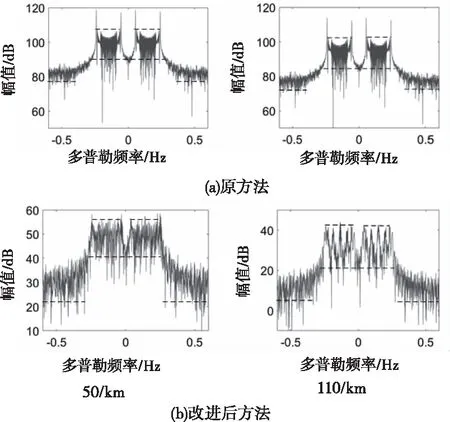
圖10 一階海雜波多普勒截面

總之，在一個相參積累周期內(nèi)，由于船載平臺的運動，不同時刻海雜波子塊的回波入射角是變化的，且不同距離元海雜波子塊回波入射角的變化規(guī)律也是不同的。這兩方面入射角度隨時間變化特點，就會導(dǎo)致海雜波分布的不一致性。因此，理論分析和實驗驗證，都證明了本文提出的海雜波改進模型與實際海雜波分布特性更為接近或有效。

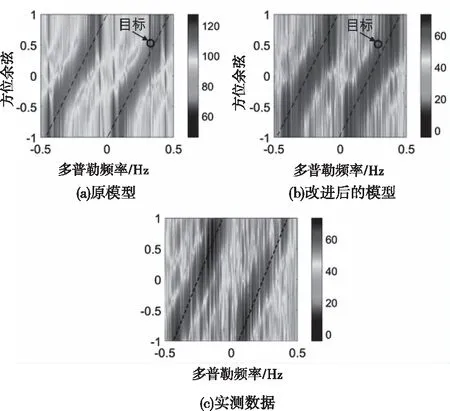
圖11 仿真模型AD譜對比

4 總結(jié)

本文針對具有均勻陣列的船載HFSWR系統(tǒng)，利用空時建模的方式，對一階海雜波的空時分布特性進行研究，并在傳統(tǒng)空時模型的基礎(chǔ)上，提出了新的改進模型。改進模型引入了船載平臺在相參積累時間內(nèi)，海雜波子塊回波入射角隨時間變化的規(guī)律，以及不同距離元海雜波子塊回波入射角隨時間變化的規(guī)律。新的海雜波仿真模型生成的一階海雜波在距離尺度上具有分布特性的不一致性。仿真結(jié)果表明，本文提出的海雜波模型相對于傳統(tǒng)海雜波模型，更貼近實測的海雜波的分布特性，為以后船載HFSWR海雜波抑制算法的研究提供有力的仿真數(shù)據(jù)支撐。

在今后的研究中，將通過更多的運動參數(shù)、不同的海況、雷達參數(shù)、以及信號傳播要素等來研究船載HFSWR海雜波的分布特性與在線抑制方法。