典型問題 常考常新 考查關鍵能力
——對2022年高考全國乙卷理綜第16 題的評析
柯 堯
(江西省九江第一中學 江西 九江 332000)
1 原題呈現
【原題】如圖1所示[1],固定于豎直平面內的光滑大圓環上套有一個小環,小環從大圓環頂端P點由靜止開始自由下滑,在下滑過程中,小環的速率正比于( )
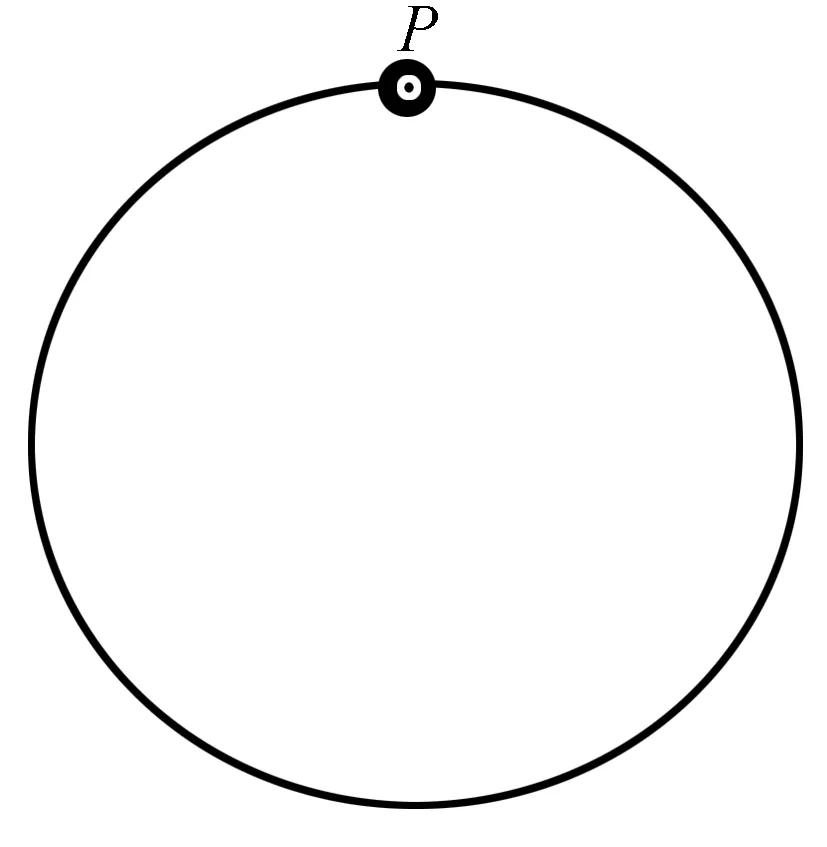
圖1 原題題圖
A.它滑過的弧長
B.它下降的高度
C.它到P點的距離
D.它與P點的連線掃過的面積
2 命題意圖
本題來源于理綜試卷物理部分第3題,屬于送分題,題文簡潔、情景常見、模型經典,但設問角度新穎,所設問題探究性強.考查了運動與相互作用觀念、能量觀念.同一個問題通過處理成不同的物理模型,選擇不同的處理方法考查了模型建構、科學推理、科學論證、質疑創新等科學思維[2].
3 問題分析
解法1:如圖2所示,設大環半徑為R,小環運動至與P點距離為l時,下降高度h,速度為v.

圖2 解法1圖
由機械能守恒定律
根據相似三角形
得
因此選項C正確.
評析:這是學生最普遍的處理方式,先根據機械能守恒定律把速度與高度關系建立,再通過幾何關系找出運動弧長、運動距離、連線掃過的面積與小環下降高度的關系.難點在于對幾何知識要求較多,運算量較大,特別是計算掃過的面積.需要學生有較強的邏輯推理、數學分析能力.
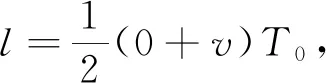
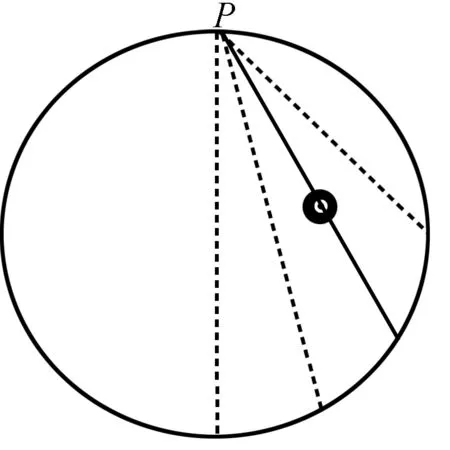
圖3 解法2圖
評析:這種解法非常巧妙、靈活,需要學生有創造性的思維,能夠想到過P點引出弦,從而利用“等時圓”的規律.學生要具備很強的運動與相互作用觀念,考查了學生的模型建構能力、質疑創新能力.
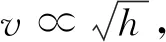
評析:采用特殊值法得出答案對于選擇題是一種很好的方式,這種采用定性與半定量的分析方式避免了繁雜的計算,這也是本套試題的一個亮點.在緊張的考試中,學生有冷靜的意志品質,有創新的處理問題意識是難能可貴的.
4 問題深究
可以根據物理規律表示出小環下滑過程速度大小隨弧長L、高度h、弦長l、掃過面積S的關系,再通過作圖軟件mathematica作出圖線直觀地反映速度隨各量變化的特點.
與弧長L的關系可以利用轉過的圓心角θ以參數方程表示為
L=Rθ
由前述知,速度與下落高度及弦長關系分別為
掃過面積與速度的關系用參數方程表示為
作出圖像如圖4~圖7所示,圖中取半徑R=1 m,重力加速度g=10 m·s-2.
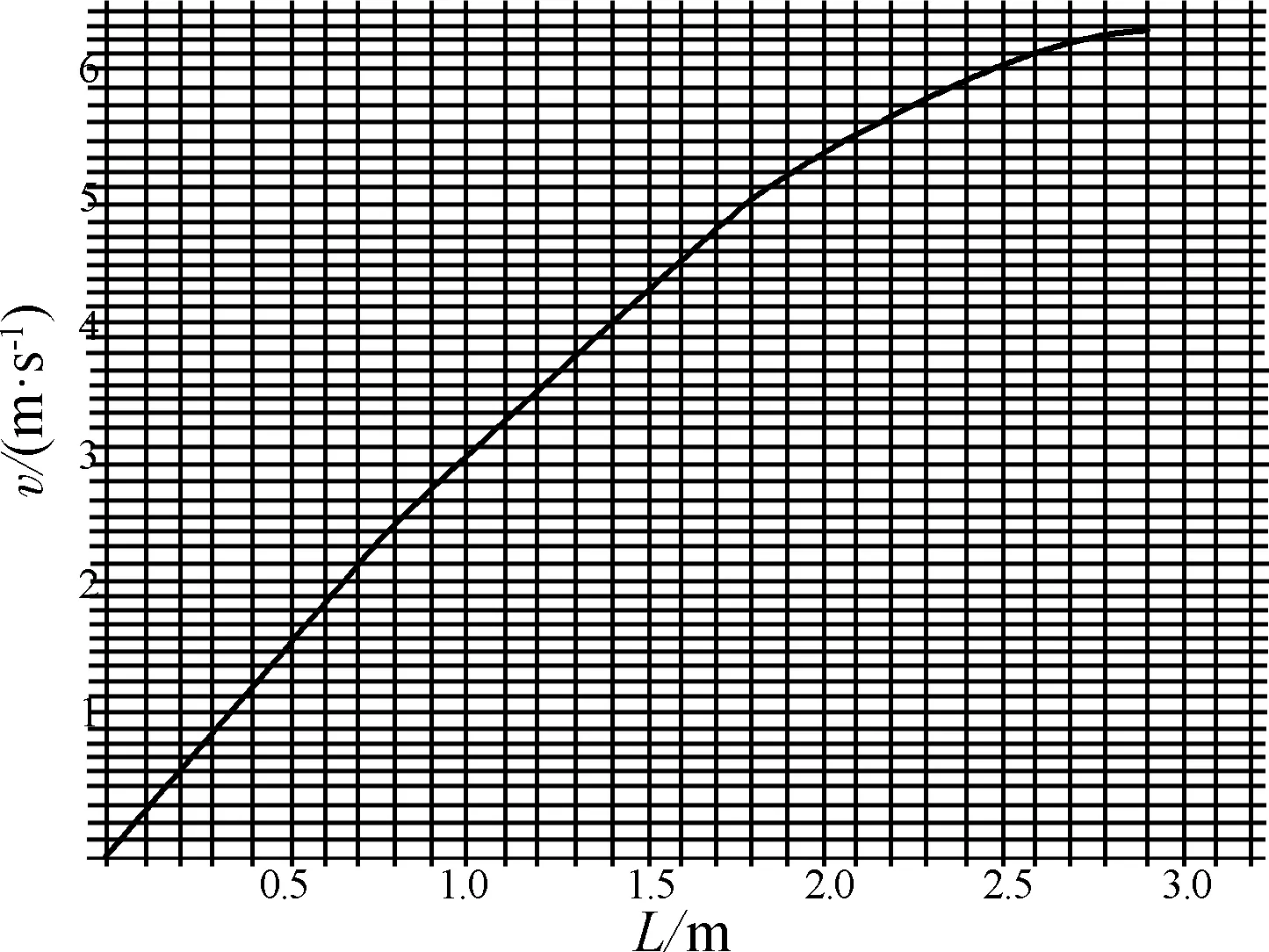
圖4 速度與下滑弧長的關系圖

圖5 速度與下滑高度的關系圖

圖6 速度與下滑弦長的關系圖

圖7 速度與下滑掃過面積的關系圖
由圖4、圖5、圖7可看出,速度明顯是非線性變化,小環下滑到圓心等高處前,速度變化較快,尤其速度隨掃過面積的變化在開始階段非常明顯,下滑至圓心下方后,速度隨各量變化較緩慢.
5 總結與教學啟示
本選擇題情景經典,設問新穎,屬于“老樹開新芽”,得到了一線教師的一致好評,有效地落實了物理學科核心素養的考查.警示了大家靠大量機械刷題考高分在高考中行不通,尤其在“雙減”背景下,對高中物理教學具有很強的指導性.
縱覽全國乙卷物理試題,命題者很好地落實了“一核”“四層”“四翼”的高考評價體系[3].對高中物理教學至少有3點重要啟示:(1)重點問題、重點方法、經典模型經常考,常考常新;(2)重視學科關鍵能力培養,尤其要重視數學能力、空間想象能力、圖像處理問題能力、模型構建能力、質疑創新能力、設計實驗探究方案能力;(3)關注物理知識“應用性”,將所學知識緊密聯系生產生活和科學技術發展.

