帶傾側角約束STT形式及BTT形式的機動飛行器速度控制方法

顏楚雄，宋加洪，秦緒國，賈平會，程云鵬

帶傾側角約束STT形式及BTT形式的機動飛行器速度控制方法

顏楚雄，宋加洪，秦緒國，賈平會，程云鵬

（北京航天長征飛行器研究所，北京，100076）

隨著飛行任務的變化，對機動飛行器進行速度控制時的運動姿態提出了新的要求。為了提高速度控制精度以及拓展該方法在多種控制方式中的應用范圍，首先，利用高斯偽譜法（Gauss Pseudospectral Method，GPM）生成理想速度曲線，為飛行器作速度控制提供可靠的速度參考曲線；然后，提出了帶傾側角約束的側滑轉彎（Skid To Turn，STT）形式以及傾斜轉彎（Bank To Turn，BTT）形式的速度控制設計方法。仿真分析表明，本文提出的方法，能夠實現對再入飛行器落速的精確控制，同時實現帶傾側角約束STT形式及BTT形式的機動飛行器速度控制。

速度控制；傾側角約束；STT；BTT

0 引 言

飛行器的末端速度是再入機動飛行器在完成飛行任務時需要滿足的終端約束之一。通常，再入飛行器中、末制導交班時速度偏大，需要采用合適的機動方式進行速度控制。通過附加攻角進行速度控制是常用的方法之一。再入飛行器在速度控制過程中，會進行大攻角與大側滑交替變化的機動飛行，各通道間耦合嚴重，飛行高度與速度變化劇烈。同時，飛行器還需要滿足約束過載、可用攻角等約束，并且保證落點和落角的終端需求。

趙漢元[1]首先提出了一種適用于再入機動飛行器的速度控制方法，并且得到了廣泛的應用；宋加洪[2]提出基于模擬飛行的再入飛行器速度控制方法，提高了再入飛行器飛行末端速度的控制精度和魯棒性；王榮剛等[3]建立了一種基于攻角和彈道傾角估計的末端減速指令生成方法，有效解決了基于理想速度曲線減速控制方法精度不足的問題；童偉等[4]提出了一種具備較強工程實用性的新型能量管控制導方法，能夠有效的降低飛行器的速度散布。

然而，傳統的速度控制方法[1]在建立理想速度曲線時進行了一定的近似和假設，使得生成的理想速度具有一定偏差，降低了理想速度曲線真實性，同時理想速度曲線的設計參數需要設計人員指定，這要求設計具有一定的工程經驗，增加了設計難度和復雜度。另一方面，常用的設計方法[1～3]通常在對飛行器進行速度控制時僅是針對側滑轉彎（Skid To Turn，STT）形式進行設計的，這局限了該方法的使用范圍。為適應復雜飛行任務，先進再入機動飛行器需要在帶傾側角約束或者傾斜轉彎（Bank To Turn，BTT）形式[5]條件下進行速度控制。

針對上述問題，本文首先利用高斯偽譜法（Gauss Pseudospectral Method，GPM）生成理想速度曲線，該曲線能夠考慮氣動力、重力以及各項約束對飛行速度產生的影響，充分反映實際飛行過程中的速度變化規律，為飛行器作速度控制提供可靠的速度參考曲線。然后，推導了帶傾側角約束的STT形式以及BTT形式的速度控制方法，滿足了對飛行器進行速度控制時的姿態要求。

1 理想速度曲線生成方法

1.1 高精度理想速度生成方法

傳統的理想速度曲線設計方法為采用理想速度經驗公式生成，工程中通常使用的帶修正系數的理想速度曲線[1]可以寫為

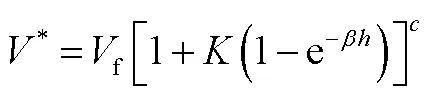
上述經驗公式由于采用了大量近似與假設會導致理想速度曲線的不準確，進而導致無法滿足高精度的速度控制需求。因此，本文提出一種基于GPM方法的理想速度曲線生成方法：首先建立再入機動飛行器動力學模型與控制模型，并考慮飛行過程中的各類約束，如過載約束、攻角約束等，然后建立目標函數，即

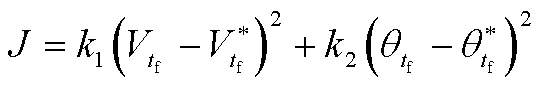
最后利用偽譜法完成對問題的離散與優化求解。偽譜法目前已較為成熟[6]，在此不做贅述。

記錄由上述方法生成的沿彈道的飛行速度作為理想速度曲線。相比于式（1）生成的理想速度曲線，用該方法生成的理想速度曲線是真實地模擬了再入機動飛行器飛行過程和飛行狀態，避免了各種簡化和近似，最大程度地反映了再入機動飛行器從中、末制導交班到落地的過程。

該方法在生成理想速度曲線時考慮了實時變化的氣動參數對再入機動飛行器的影響，并通過再入機動飛行器的控制能力，對彈道進行了修正；同時，該方法生成的理想速度，已經考慮了阻力對速度的影響，因此不再需要預留速度偏差，可以隨時在比例導引和速度控制間切換。

1.2 速度控制指令

根據第1.1節得到的理想速度曲線，生成速度控制指令的方法為：

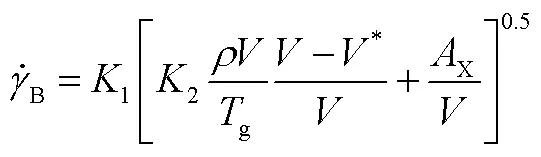
2 多樣式速度控制設計方法

2.1 STT形式下的速度控制方法

帶落角約束的比例導引律為

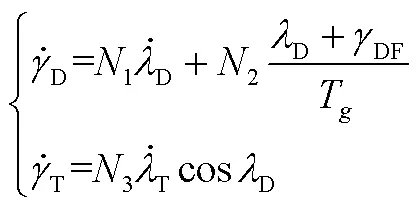
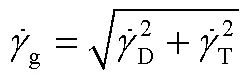
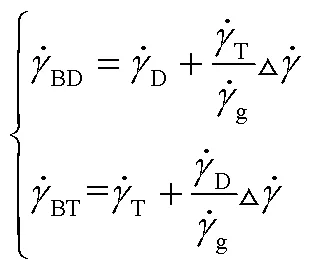
且

因此，可以計算得到：

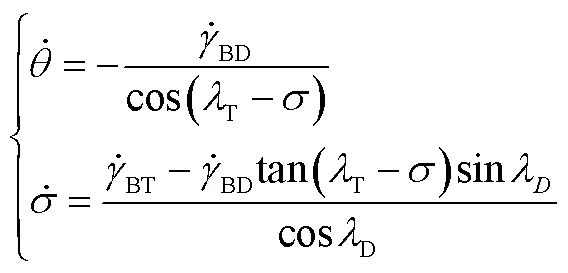
進而求得需用過載：

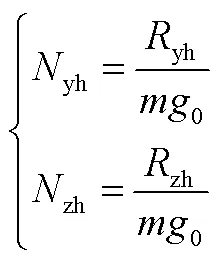
進一步考慮半速度坐標系與速度坐標系的轉換關系，即

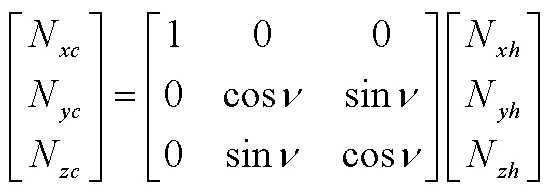
由此得到指定傾側角約束情況下的實際需用過載。

2.2 BTT-180形式下的速度控制方法

首先，利用式（10）求出半速度坐標系內的需用過載。當采用BTT-180控制策略時，根據半速度坐標系內的過載計算得到需用的總過載，即

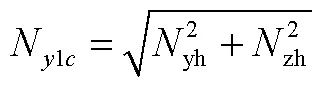
同時，利用反正切函數計算傾側角，計算得到的傾側角范圍為[-π，π]。

對于BTT-180模式，傾側角指令的計算方法為

為在連續速度控制時以及加速度等于0時引入數學的奇異性，即由于垂直或者側向制導指令微小的變化而出現很大的變動，傾側角會在-π和π之間出現跳變，需要對直接用反正切函數求出的傾側角進行修正。

為解決該問題，可以先利用式（14）和式（15）計算1和2，即：

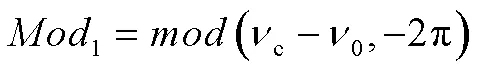
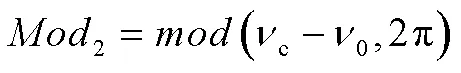
3 仿真校驗

首先檢驗第1.1節提出的高精度理想速度曲線生成方法對落速控制的作用。根據1.1節的方法生成一條參考的理想速度曲線，然后以此為基礎，進行速度控制。在上述仿真中，都采用STT形式的速度控制方法。

圖1和圖2給出了飛行器在速度控制過程中，各狀態變量變化情況。

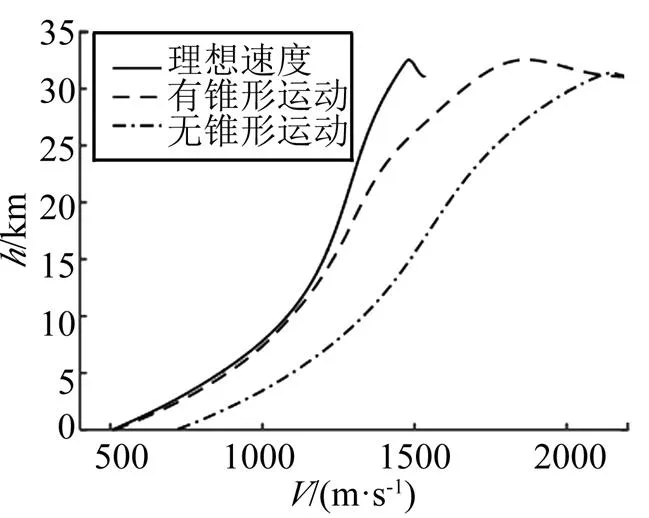
圖1 飛行器速度控制效果

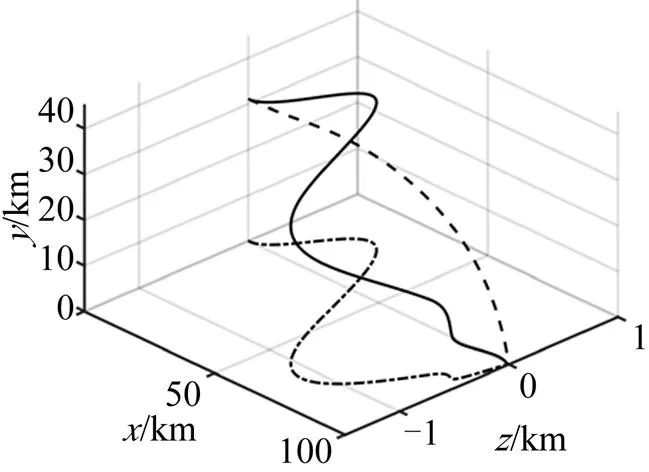
圖2 飛行器運動軌跡

由圖1可知，通過速度控制，再入飛行器能夠進行減速，達到期望的落速。相較于未減速時的715 m/s的落速，利用該方法，飛行器落速可以減到503 m/s，符合設計要求。生成的理想速度曲線作為速度控制的參考曲線，為參考指令提高了良好依據。

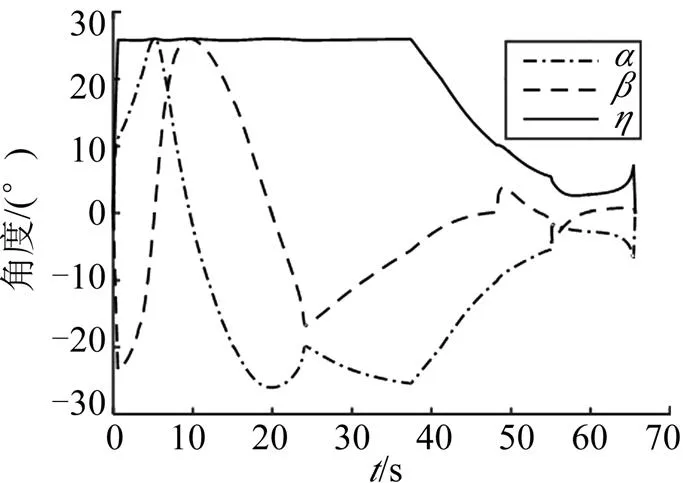
圖3 STT形式角度變化情況()

利用第2.1節提出的速度控制設計方法，進行帶傾側角約束的速度控制機動。分別設計了傾側角為30°（見圖4）、傾側角為90°（見圖5）以及變傾側角（見圖6）的速度控制機動方式。通過仿真可以看出，通過應用本文提出的帶傾側角約束的速度控制方法，飛行器可以完成指定傾側角以及變傾側角的速度控制。

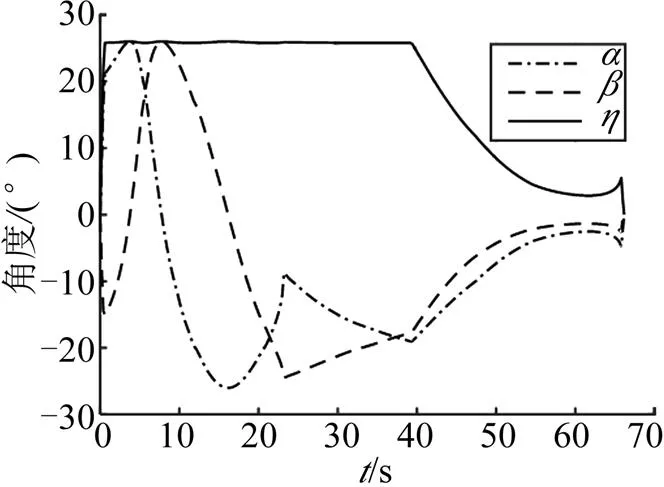
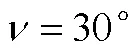
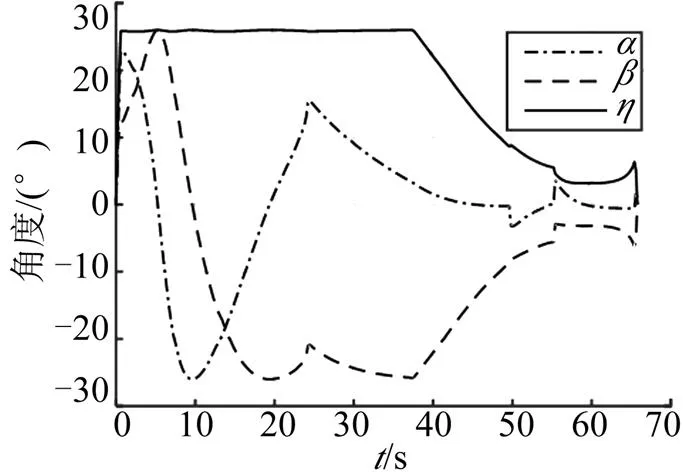
圖5 STT形式角度變化情況()

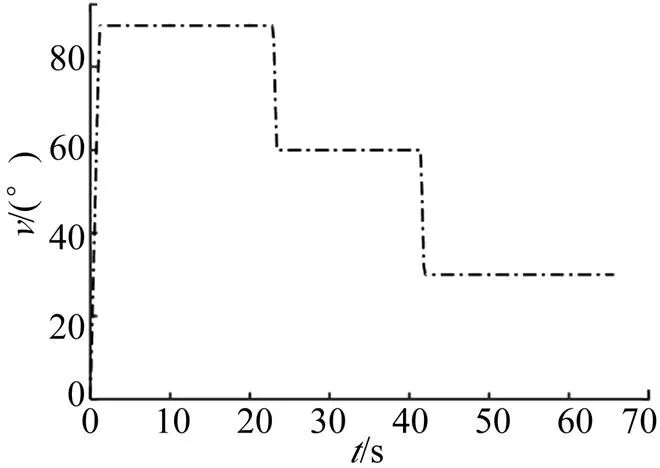
利用第2.1節的設計方法，還可以設計傾側角為180°的速度控制機動方法（如圖7）。

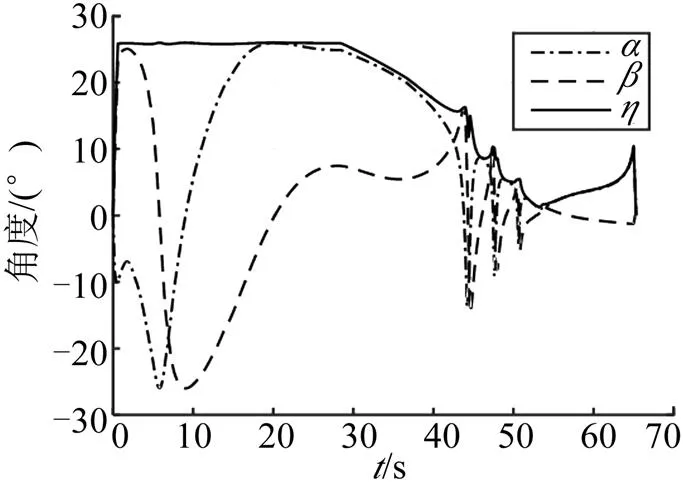
圖7 STT形式角度變化情況()

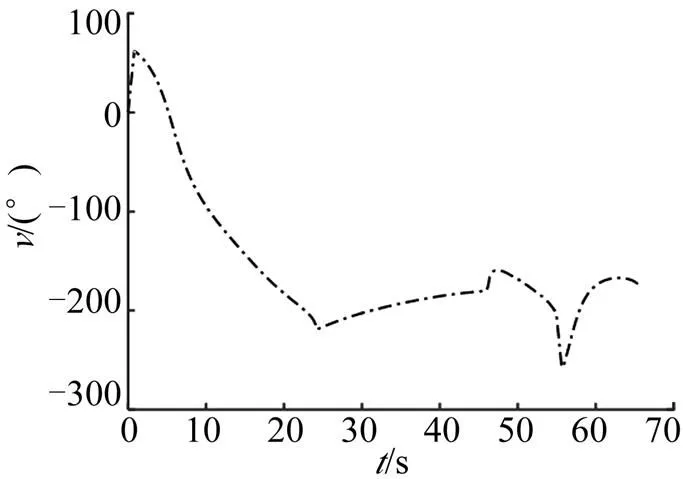
采用BTT-180控制形式進行速度控制，BTT形式角度變化情況如圖8所示。從圖8中可以看出，側滑角始終保持在0°，傾側角連續變化。應用第2.2節的傾側角修正方法，傾側角避免了在-π和π之間出現跳變。在BTT-180控制形式下，速度控制不再是攻角與側滑角交替變化，而是攻角始終保持最大值，側滑角保持在0°，傾側角連續變化，從而在有限的飛行距離中，增加了下壓過程中的飛行航程，在空間中進行側向機動，通過增加使用攻角，誘導阻力增加，進而達到速度控制的目的。

4 結束語

對機動飛行器基于理想速度曲線設計的速度控制方法進行了改進設計與應用。首先利用GPM方法生成理想速度曲線，該曲線能夠考慮氣動力、重力以及各項約束對飛行速度產生的影響，充分反映實際飛行過程中的速度變化規律，為飛行器作速度控制提供可靠的速度參考曲線。同時，推導了帶傾側角約束的STT形式以及BTT形式的速度控制方法，實現了多控制形式下的落速控制，實現了指定傾側角、變傾側角和翻身條件下的速度控制，滿足了各類飛行任務需求，擴展了基于理想速度曲線設計的速度控制的應用范圍。

[1] 趙漢元. 飛行器再入動力學和制導[M]. 長沙: 國防科學技術大學出版社, 1997.

Zhao Hanyuan. Dynamics and guidance of reentry vehicle[M]. Changsha:

National University of Defense Technology Press, 1997.

[2] 宋加洪. 基于模擬飛行的再入飛行器速度控制方法[J]. 導彈與航天運載技術, 2012(2): 4-7.

Song Jiahong. A velocity control method of the reentry vehicle based on flight simulation[J]. Missiles and Space Vehicles, 2012(2): 4-7.

[3] 王榮剛, 等. 高超聲速滑翔再入定向定速打擊末制導算法[J]. 宇航學報, 2019, 40(6): 655-665.

Wang Ronggang, et al. Ter-minal guidance with impact angle constraint and deceleration control for a hypersonic glide-reentry vehicle[J]. Journal of Astronautics, 2019, 40(6): 655-665.

[4] 童偉, 等. 遠程機動飛行器能量管控制導方法[J]. 導彈與航天運載技術, 2021(04): 88-92.

Tong Wei, et al. Research of energy management and control strategy for long range maneuvering vehicle[J]. Missiles and Space Vehicles, 2021(04): 88-92.

[5] 葉振信, 李傳峰, 傅維賢, 王萬軍. 大氣層內無動力滑翔炸彈傾斜轉彎控制設計[J]. 導彈與航天運載技術, 2010(06): 6-9.

Ye Zhenxin, Li Chuanfeng, Fu Weixian, Wang Wanjun. Bank-to-turn control design for no-power gliding bomb inside atmosphere[J]. Missiles and Space Vehicles, 2010(06): 6-9.

[6] Michael A P, William W H, Anil V R. A ph mesh refinement method for optimal control[J]. Optim. Control Appl. Meth., 2015(36): 398-421.

A Velocity Control Methodof the Maneuvering Vehicle in STT Style with the Constraint of Bank Angle and BTT Style

Yan Chu-xiong, Song Jia-hong, Qin Xu-guo, Jia Ping-hui, Cheng Yun-peng

(Beijing Institute of Space Long March Vechile, Beijing, 100076)

With the change of the flight mission, the new pose requirement in the velocity control method is proposed. The research aims to improve the accuracy of the velocity control method and expand its application scope in different control method. The ideal velocity control curve is generated by using the Gauss Pseudospectral method, which is offered as the reliable velocity reference curve. Then, the velocity control method in STT style with the constraint of bank angle and BTT style is derived. The simulation results show that the proposed method can control the final velocity of reentry vehicle accurately, and realize the velocity control in STT style with the constraint of bank angle and BTT style.

velocity control; the constraint of bank angle; STT; BTT

2097-1974(2023)01-0127-05

10.7654/j.issn.2097-1974.20230125

V412

A

2022-11-10；

2022-12-01

顏楚雄（1991-），男，博士，工程師，主要研究方向為飛行力學。

宋加洪（1972-），男，博士，研究員，主要研究方向為飛行力學。

秦緒國（1984-），男，博士，研究員，主要研究方向為飛行器總體設計。

賈平會（1988-），男，高級工程師，主要研究方向為飛行力學。

程云鵬（1992-），男，博士，工程師，主要研究方向為飛行力學。