熱載荷下儀表螺紋連接狀態(tài)的機電阻抗概念驗證研究

付雨露, 王瑞強, 孫清超, 沙 立, 凌林本

（1. 大連理工大學(xué)機械工程學(xué)院, 大連 116024;2. 北京航天控制儀器研究所, 北京 100039）

0 引言

高精度慣性儀表是一種重要的慣性導(dǎo)航器件,廣泛應(yīng)用于航空、 航天及船舶等領(lǐng)域, 對裝配工藝的要求極高。 尤其是隨著精度要求的不斷提高,組件結(jié)構(gòu)的穩(wěn)定性成為目前研究的焦點。 其內(nèi)部溫度變化顯著, 工作精度與其周圍溫度環(huán)境和內(nèi)部工作環(huán)境有著密切的關(guān)系［1-3］。 螺紋連接是慣性儀表裝配過程中大量應(yīng)用的連接方式之一, 儀表內(nèi)部存在的溫度梯度極容易引起螺紋連接結(jié)構(gòu)的松動, 對浮子組件的平衡產(chǎn)生影響, 引起轉(zhuǎn)子質(zhì)心漂移, 從而導(dǎo)致慣性儀表的運動精度降低乃至失效。 因此, 開展對溫度變化下精密慣性儀表螺紋連接結(jié)構(gòu)健康狀況的檢測是十分必要的。

機電阻抗（Electromechanical Impedance, EMI）方法具有局部靈敏度高、 便于安裝、 無需模型分析等優(yōu)點, 在復(fù)雜結(jié)構(gòu)實時在線監(jiān)測領(lǐng)域具有獨特的優(yōu)勢。 最早是LIANG 等［4］提出了EMI 技術(shù),利用壓電材料的正壓電效應(yīng)與逆壓電效應(yīng), 實現(xiàn)了機械能與電能之間的轉(zhuǎn)換。 對粘貼在結(jié)構(gòu)表面的壓電材料施加激勵電壓, 壓電元件振動, 通過耦合作用將振動傳遞到結(jié)構(gòu)上。 與此同時, 結(jié)構(gòu)的振動會使得壓電元件發(fā)生變形, 從而使得電阻抗發(fā)生改變, 以此來檢測結(jié)構(gòu)是否健康。 眾多研究［5-7］表明, EMI 技術(shù)可以用于結(jié)構(gòu)的損傷監(jiān)測及損傷識別, 然而溫度對EMI 技術(shù)的影響也是不可忽略的, 溫度會直接影響EMI 方法檢測的準確性。KRISHNAMURTHY 等［8］研究并發(fā)現(xiàn)了介電常數(shù)對溫度十分敏感。 閻石等［9］研究了溫度對壓電智能骨料信號的穩(wěn)定性并分析了變化規(guī)律, 發(fā)現(xiàn)溫度對信號的影響是非線性的, 且信號在每個溫度節(jié)點上都較為穩(wěn)定。 SEPEHRY 等［10-11］在梁表面粘貼了壓電陶瓷（Piezoelectric Lead Zirconate Titanate, PZT）片, 制成一種歐拉-伯努利梁, 探究了機械阻抗受溫度的影響規(guī)律, 并進行了數(shù)值計算和比較。

以上研究大多集中在土木領(lǐng)域的梁、 殼結(jié)構(gòu)上, 而對于復(fù)雜精密機械結(jié)構(gòu)的研究還較少。 同時, 針對溫度的相關(guān)研究中, 對于儀表內(nèi)部交變溫度載荷下連接結(jié)構(gòu)健康檢測問題并不完全適用。因此, 本文以慣性儀表動壓氣浮軸承結(jié)構(gòu)為研究對象, 結(jié)合PZT 導(dǎo)納及阻抗公式驗證了機電阻抗技術(shù)識別螺紋連接狀態(tài)的可行性, 并分析了溫度對機電阻抗的影響。 通過有限元仿真方法, 探究了交變溫度對PZT 阻抗信號的影響規(guī)律, 構(gòu)建精密儀表內(nèi)部溫度場環(huán)境, 對溫度變化下的阻抗信號進行了分析, 驗證了仿真模型的正確性。 獲得了溫度變化對機電阻抗監(jiān)測技術(shù)的影響規(guī)律, 可以作為精密慣性儀表健康監(jiān)測方法的參考。

1 EMI 技術(shù)的溫度效應(yīng)

PZT 貼片實質(zhì)上是一個平行板電容器, 壓電材料是其電介質(zhì)材料, 而壓電效應(yīng)是壓電材料的固有屬性, 可以實現(xiàn)機械能與電能之間的轉(zhuǎn)換。 PZT自身存在正逆壓電效應(yīng), 如圖1 所示, 集激勵與傳感于一體, 所以既可以作為驅(qū)動器又可以作為傳感器。 給PZT 一個激勵, 電場會發(fā)生變化, 也會產(chǎn)生機械應(yīng)變。

圖1 壓電材料的正逆壓電效應(yīng)Fig.1 Positive and negative piezoelectric effects of piezoelectric materials

將PZT 粘貼在結(jié)構(gòu)上, 它會與結(jié)構(gòu)進行耦合。在交流電壓的激勵下, PZT 在軸向上發(fā)生振動, 而結(jié)構(gòu)的機械阻抗將約束PZT 的運動。 系統(tǒng)的耦合模型如圖2 所示。

圖2 單自由度-質(zhì)量-剛度-阻尼系統(tǒng)的耦合模型Fig.2 Coupling model of single degrees of freedom-mass-stiffness-damping system

與結(jié)構(gòu)耦合的電導(dǎo)納及電阻抗表達式如下

螺紋連接松動、 預(yù)緊力減小會使結(jié)構(gòu)機械阻抗變化, 從而導(dǎo)致耦合阻抗發(fā)生改變。 而溫度會影響壓電材料的壓電應(yīng)變常數(shù)d31及介電常數(shù)εT31,也會使得耦合阻抗改變。 溫度對壓電應(yīng)變常數(shù)的影響呈線性關(guān)系, PZT 與結(jié)構(gòu)的耦合阻抗會因此發(fā)生變化。 隨著溫度的升高, 壓電材料的介電常數(shù)呈指數(shù)增長, 這使得PZT 的電容C隨之變大, 耦合阻抗隨之改變。 因此, 在結(jié)構(gòu)未受損傷, 即結(jié)構(gòu)機械阻抗不變時, 溫度變化也會影響PZT 的阻抗信號。 溫度對阻抗信號的影響較為復(fù)雜, 并非對壓電應(yīng)變常數(shù)、 介電常數(shù)影響的簡單疊加, 進一步探究溫度對PZT 阻抗信號的影響規(guī)律, 研究溫度效應(yīng)的修正技術(shù)以增加機電阻抗技術(shù)的適用性具有重要意義。

2 多物理場耦合仿真

機電阻抗分析涉及靜電場、 物理場的耦合,利用COMSOL 進行多物理場耦合仿真, 探究溫度對阻抗信號的影響。 在慣性儀表中, 陀螺電機轉(zhuǎn)子、 安裝框架、 半球軸承連同電機軸統(tǒng)稱為轉(zhuǎn)子系統(tǒng), 如圖3 所示。 高精度陀螺儀表采用動壓氣浮軸承進行支撐, 可以提高電機使用壽命和陀螺儀精度, 動壓氣浮軸承的穩(wěn)定性受螺紋連接狀態(tài)影響。 對半球型動壓氣浮軸承結(jié)構(gòu)進行仿真分析,仿真根據(jù)精密儀表的實際熱載荷工況進行設(shè)置。

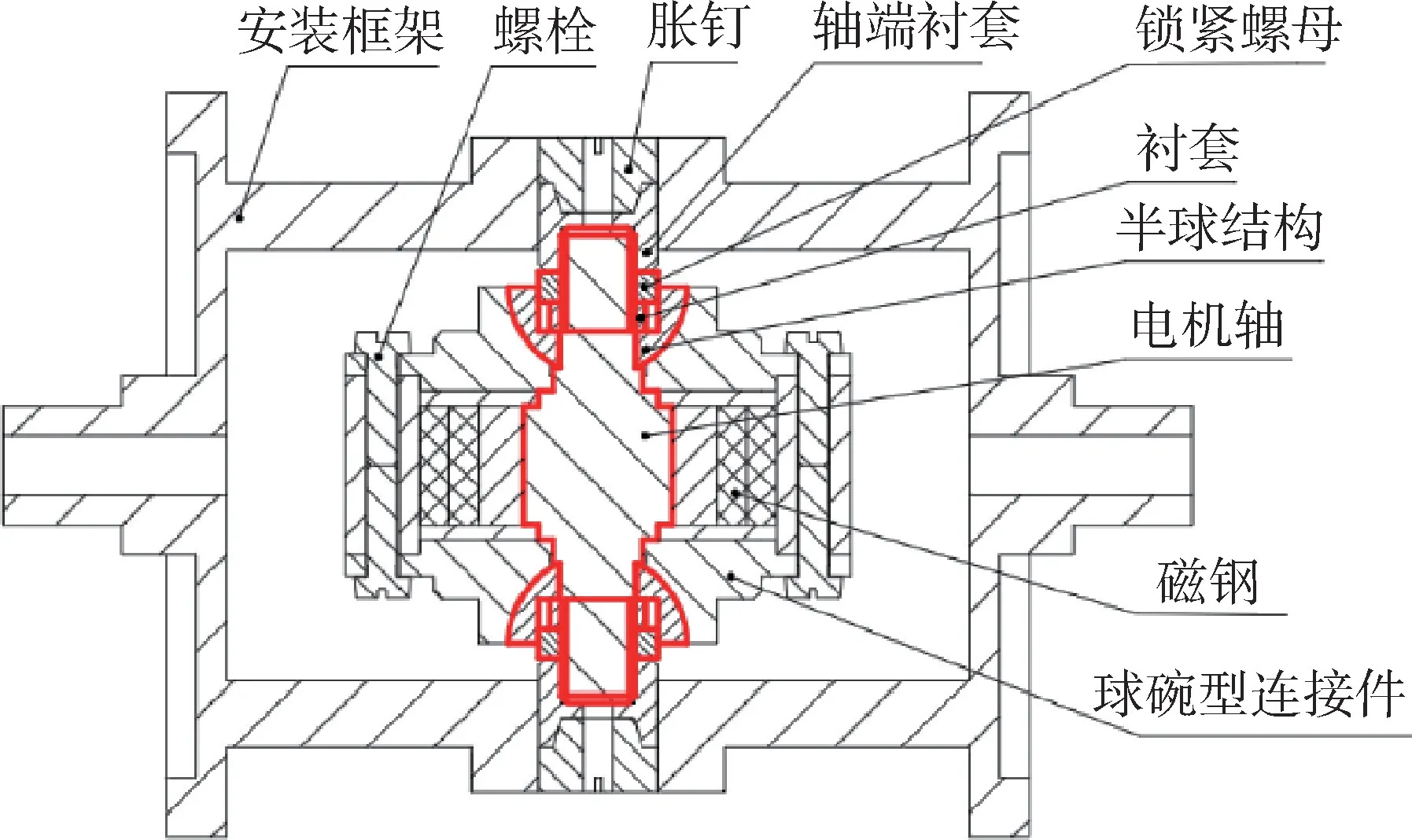
圖3 轉(zhuǎn)子系統(tǒng)結(jié)構(gòu)圖Fig.3 Structure diagram of rotor system

半球型動壓氣浮軸承結(jié)構(gòu)的上連接件為半球結(jié)構(gòu), 鎖緊螺母通過軸端的螺紋擰緊在軸的兩端。為了防止球碗型連接件的連接面受力不均勻, 在鎖緊螺母與上連接件之間添加襯套, 如圖4（a）所示。 為了與后續(xù)試驗?zāi)Ｐ鸵恢? 根據(jù)儀表結(jié)構(gòu)對動壓氣浮軸承結(jié)構(gòu)進行等比例放大, 軸端螺紋公稱直徑為10mm。 儀表結(jié)構(gòu)為對稱分布, 在此本文只選擇一端螺紋連接結(jié)構(gòu)作為研究對象, 探究溫度對阻抗信號的影響規(guī)律。 仿真中對螺紋進行簡化處理, 使用一半結(jié)構(gòu)進行仿真分析, 模型如圖4（b） 所示。 其中, PZT 為Φ5mm × 0.5mm 的PZT-5H 型壓電陶瓷片, 電機軸材料為45 鋼。

圖4 半球型動壓氣浮軸承結(jié)構(gòu)及仿真模型Fig.4 Schematic diagram of hemispherical dynamic pressure air bearing structure and simulation model

采用COMSOL 自帶的螺栓預(yù)緊力節(jié)點施加預(yù)緊力, 如圖5 所示, 將軸視作螺桿, 設(shè)置一個穿過軸的截面, 預(yù)緊力節(jié)點施加在該截面上使得軸內(nèi)部產(chǎn)生拉應(yīng)力, 這時產(chǎn)生的反作用力表現(xiàn)為螺栓預(yù)緊力, 預(yù)緊力設(shè)置為30000N。 仿真中保持預(yù)緊力加載, 使鎖緊螺母處于緊固連接狀態(tài)。

圖5 螺栓預(yù)緊力截面Fig.5 Schematic diagram of bolt preload section

將結(jié)構(gòu)各個接觸面設(shè)置為“一致對”, 即認為相互接觸的部件為一個構(gòu)件, 接觸面間的物理場是連續(xù)的, 以保證結(jié)果收斂。 將螺母上端面設(shè)置為彈簧基礎(chǔ), 被連接件的下底面設(shè)置為固定約束,如圖6 所示, 使用增廣拉格朗日求解法進行求解。PZT 置于軸端面中心的位置, PZT 和結(jié)構(gòu)耦合的端面設(shè)置接地, 另一端面設(shè)置電壓終端, 采用COMSOL 內(nèi)部的linper 函數(shù)施加1V 交流電壓。 linper 函數(shù)可以確保施加的電壓只用于線性擾動求解器中,確保穩(wěn)態(tài)求解器不受其影響。

圖6 彈簧基礎(chǔ)與固定約束Fig.6 Schematic diagram of spring base and fixed constraints

采用COMSOL 自帶的四面體網(wǎng)格對試件進行劃分, 如圖7 所示。

圖7 試件網(wǎng)格劃分Fig.7 Schematic diagram of specimen meshing

由第1 節(jié)中對耦合阻抗的理論分析可知, 溫度主要影響PZT 的壓電應(yīng)變常數(shù)及介電常數(shù)。 然而,介電常數(shù)由相對介電常數(shù)εr決定（εT=εr·ε0,ε0為真空介電常量）。 當PZT 粘貼于結(jié)構(gòu)表面時,PZT 將其平面的拉伸和壓縮與結(jié)構(gòu)表面彈性波的平面彈性應(yīng)變相耦合。 平面PZT 的運動是通過d31和d32壓電效應(yīng)激勵, 而其他方向上的壓電應(yīng)變常數(shù)影響不大。 因此, 在進行壓電應(yīng)變常數(shù)設(shè)置時,僅改變d31和d32, 其余方向上的壓電應(yīng)變常數(shù)保持不變。 不同溫度下的PZT-5H 參數(shù)如表1 所示, 根據(jù)表1 參數(shù)設(shè)置不同溫度下的PZT 參數(shù), 探究溫度對阻抗信號的影響。

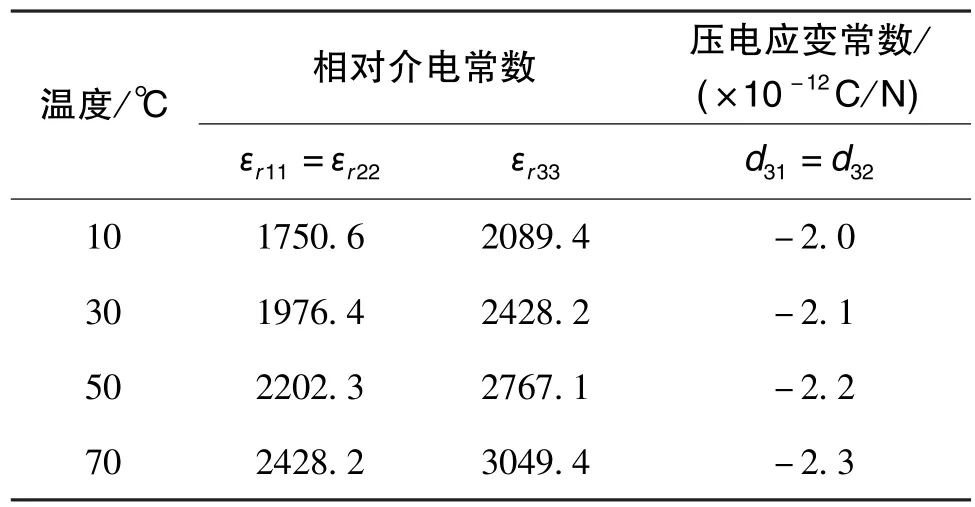
表1 不同溫度下的PZT 參數(shù)Table 1 PZT parameters at different temperatures

為了確定阻抗峰值特征明顯的頻率區(qū)間, 仿真首先粗略掃描了200kHz ～1800kHz 頻段范圍,掃描步長設(shè)置為3kHz, 阻抗實部曲線如圖8 所示。

圖8 200kHz ～1800kHz 的阻抗實部曲線Fig.8 Impedance real part curve in 200kHz ～1800kHz

由圖8 可知, 在200kHz ～1800kHz 頻率范圍內(nèi)出現(xiàn)了6 個波峰。 由于PZT 本身存在共振頻率,所以能量在不同的頻段內(nèi)也是不同的。 在激勵電壓的作用下, 某些頻率點產(chǎn)生能量集中, 反映在阻抗實部曲線上就形成波峰。 由于波峰反映結(jié)構(gòu)固有特性且相對敏感, 而在870kHz ～970kHz、1470kHz ～1570kHz 兩個頻段內(nèi)出現(xiàn)了較為明顯的波峰, 因此后續(xù)仿真在870kHz ～970kHz、 1470kHz～1570kHz 兩個頻段內(nèi)進行精細掃描。

仿真溫度分別設(shè)置為10℃、 30℃、 50℃、70℃, 掃描步長均為1kHz。 圖9 為不同激勵頻段內(nèi)阻抗實部曲線波峰隨溫度的變化情況。 由圖9 可知, 隨著溫度升高, 兩個波峰均發(fā)生峰值頻率的左移和高度的降低。 但是不同頻段內(nèi), 波峰的變化程度不同: 在頻段870kHz ～970kHz 內(nèi), 溫度從10℃升高到70℃的過程中, 阻抗實部曲線的峰值頻率從920kHz 變化到了919kHz, 共降低1000Hz;在頻段1470kHz ～1570kHz 內(nèi), 溫度從10℃升高到70℃的過程中, 阻抗實部曲線的峰值頻率從1510kHz 變化到了1505kHz, 共降低5000Hz。 峰值幅值的變化在不同頻段內(nèi)也是有差異的: 在頻段870kHz ～970kHz 內(nèi), 隨著溫度升高到70℃, 阻抗波峰幅值下降了4.59Ω; 而在頻段1470kHz ～1570kHz 內(nèi), 隨著溫度升高到70℃, 阻抗波峰幅值僅下降1.13Ω。

圖9 溫度變化對阻抗實部信號的影響Fig.9 Effect of temperature changes on the impedance real part signal

仿真結(jié)果表明, 溫度變化會對阻抗信號的峰值頻率和幅值造成影響, 溫度升高會造成阻抗實部信號峰值頻率的左移及波峰幅值的下降。 并且溫度對阻抗實部信號的影響與頻率有關(guān), 在低頻范圍內(nèi), 溫度對峰值頻率的影響較小, 而對波峰幅值的影響較為顯著。

3 溫度影響試驗

為了模擬精密儀表服役時的工況及熱載荷作用,采用可程式恒溫恒濕試驗箱、 阻抗測試系統(tǒng)、 電子溫度計組成的試驗系統(tǒng)進行溫度試驗。 其中, 筆記本電腦及精密阻抗分析儀構(gòu)成阻抗測試系統(tǒng), 用來檢測粘在結(jié)構(gòu)上的PZT 阻抗。 溫箱用來進行溫度的調(diào)節(jié)及保持, 由于溫箱內(nèi)腔過大, 在溫箱內(nèi)部不同區(qū)域可能會出現(xiàn)溫度不均勻的現(xiàn)象, 使用電子溫度計來檢測試驗件周圍區(qū)域的溫度, 試驗時溫度以電子溫度計示數(shù)為準。 試驗裝置如圖10 所示。

圖10 試驗裝置Fig.10 Diagram of test equipment

PZT 采用直徑為10mm、 厚度為0.5mm 的PZT-5H 型圓形壓電陶瓷片, 重要性能參數(shù)如表2 所示。

表2 PZT 重要性能參數(shù)Table 2 Important performance parameters of PZT

在不影響試驗結(jié)果的前提下, 為了方便粘貼PZT, 對慣性儀表動壓氣浮軸承結(jié)構(gòu)進行等比例放大。 試驗件的軸端分別帶有長度為14mm 的M12的螺紋, 軸中間部位直徑為17mm, 總長度為102mm。 采用406 瞬干膠將PZT 粘在試驗件頭部,粘貼后的試驗件如圖11 所示。 用膠帶將連接線粘在試驗件表面, 防止連接線在誤觸、 拉扯等情況下斷裂。

圖11 粘貼PZT 的試驗件Fig.11 Diagram of test pieces with PZT

將試驗件粘有PZT 的一端夾持在臺面虎鉗上,用扭矩扳手對試驗件沒有PZT 及連線的一端進行加載, 以防止試驗過程中套筒損壞連接線, 加載扭矩為20N·m。 將粘有PZT 的試驗件置于溫箱內(nèi), 溫度分別設(shè)置為20℃、 30℃、 40℃、 50℃、60℃。 溫箱內(nèi)腔溫度到達設(shè)定值之后進行溫度保持, 讓溫箱內(nèi)腔與試驗件熱交換完全并建立熱平衡, 以減小試驗件溫度不均造成的試驗誤差, 保持時間為30min, 待電子溫度計示數(shù)穩(wěn)定之后進行掃描。 之后采用精密阻抗分析儀激勵PZT, 激勵電壓為1V, 采集PZT 的阻抗信號并保存。 一次溫度試驗完成后取出試驗件, 采用扭矩扳手進行卸載,靜置一段時間, 試驗件恢復(fù)成室溫后再加載、 調(diào)溫, 再進行下一次溫度試驗, 保持每次試驗的一致性, 減小試驗誤差。

為了找到特征峰出現(xiàn)的頻率帶, 先在100kHz ～700kHz 范圍內(nèi)進行掃描, 確定適當?shù)念l率區(qū)間進行精細掃描, 研究該頻率區(qū)間內(nèi)阻抗特征峰的變化規(guī)律。 在20℃～60℃溫度范圍內(nèi)掃描PZT 的電阻抗值, 掃描頻段為100kHz ～700kHz, 掃描步長為0.3kHz, 激勵電壓為1V, 阻抗實部曲線如圖12所示。

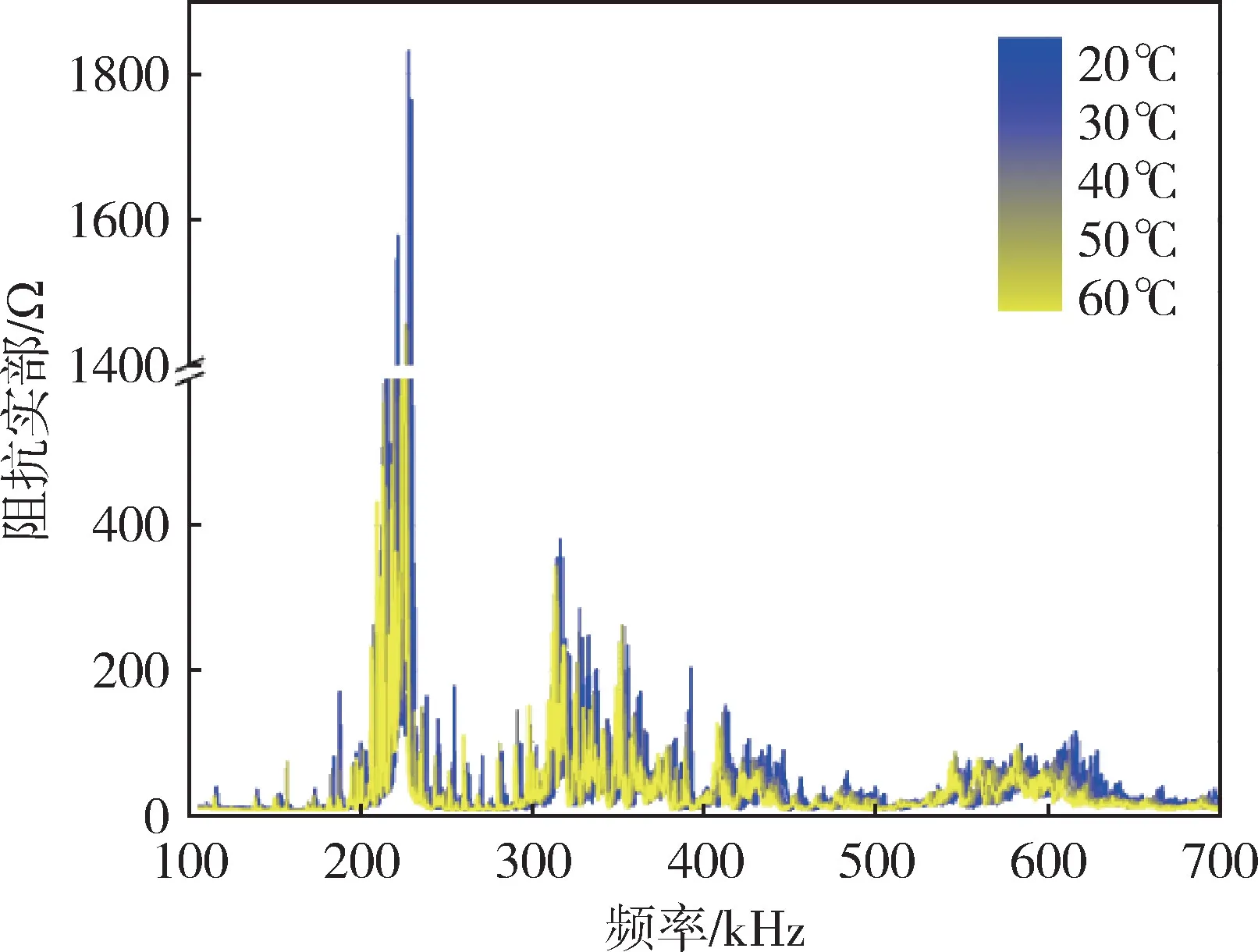
圖12 100kHz ～700kHz 的阻抗實部曲線Fig.12 Impedance real part curves in 100kHz ～700kHz

由圖12 可知, 在150kHz ～250kHz、 300kHz ～400kHz、 550kHz ～650kHz 范圍內(nèi)都有明顯的波峰。但是, 在150kHz ～250kHz 范圍內(nèi)的波峰幅值過大, 且多次試驗表明該頻段內(nèi)阻抗信號一致性差,容易受到噪聲等外界因素干擾; 在550kHz ～650kHz 范圍內(nèi)波峰不太明顯, 且比較雜亂, 對環(huán)境變化的敏感性較差。 因此, 選取300kHz ～400kHz 頻段進行精細掃描, 掃描步長為0.2kHz,溫度范圍為20℃～60℃, 每10℃為一個溫度節(jié)點,阻抗實部曲線如圖13 所示。

圖13 300kHz ～400kHz 的阻抗實部曲線Fig.13 Impedance real part curves in 300kHz ～400kHz

由圖13 可知, 溫度會影響阻抗曲線的峰值頻率和峰值幅值。 溫度從20℃變化到60℃的過程中,阻抗實部曲線會發(fā)生峰值頻率向左偏移和波峰幅值下降的現(xiàn)象。

為避免不同溫度下的阻抗實部曲線發(fā)生重疊,以便明顯觀察峰值頻率的偏移, 將其繪制為Y偏移堆積線圖, 如圖14 所示。 由圖14 可知, 溫度升高會使阻抗實部曲線峰值頻率降低, 且幅值也會下降。 在不同的頻段內(nèi), 阻抗實部曲線受溫度影響的變化趨勢相同, 但是峰值頻率向左偏移的程度不同。 在相對低的頻段范圍內(nèi), 峰值頻率向左偏移比較少, 而幅值的變化更加顯著。 即隨著頻率的降低, 溫度對峰值頻率的影響逐漸變?nèi)? 溫度對波峰幅值的影響逐漸顯著。 阻抗實部曲線峰值頻率隨溫度的偏移情況如表3 所示。

表3 峰值頻率隨溫度的偏移情況Table 3 Peak frequency offsets with temperature

圖14 不同溫度下的阻抗實部曲線Fig.14 Impedance real part curves at different temperatures

分析表3 中數(shù)據(jù)可知, 隨著溫度的升高, 阻抗實部曲線峰值頻率會向左偏移, 但是偏移程度會受頻率的影響。 溫度在從20℃升高到60℃的過程中, 1 # 峰的峰值頻率從 328.71kHz 變化到324.49kHz, 共降低了4.22kHz; 2#峰的峰值頻率從 355.61kHz 變化到 351.01kHz, 共降低了4.60kHz; 3#峰的峰值頻率從392.83kHz 變化到387.79kHz, 共降低了5.04kHz。 在從20℃升高到60℃的過程中, 頻率越高, 峰值頻率向左偏移的現(xiàn)象就越加明顯。 也就是說, 溫度對峰值頻率的影響隨著頻率的升高而更加顯著。

表4 為阻抗實部曲線波峰幅值隨溫度的變化情況。 分析表4 中數(shù)據(jù)可知, 溫度升高, 阻抗實部曲線波峰幅值會下降, 下降程度受到頻率的影響。溫度在從20℃升高到60℃的過程中, 1#峰的波峰幅值從305.51Ω 變化到174.20Ω, 共下降了131.31Ω; 2#峰的波峰幅值從313.67Ω 變化到218.39Ω, 共下降了95.28Ω; 3#峰的波峰幅值從203.23Ω 變化到108.57Ω, 共下降了94.66Ω。 在從20℃升高到60℃的過程中, 頻率越高, 波峰幅值下降的越少, 即溫度對波峰幅值的影響隨著頻率的增大而減小。

試驗表明, 溫度會影響PZT 阻抗實部信號的峰值頻率和波峰幅值, 溫度升高, 阻抗實部曲線的峰值頻率會向左偏移, 波峰幅值也會下降。 并且溫度對導(dǎo)納信號的影響與頻率有關(guān), 在同一溫度下, 頻率越低, 阻抗實部信號峰值頻率向左偏移程度越小, 而波峰幅值下降越多。 在低頻范圍內(nèi), 溫度對峰值頻率的影響較小, 溫度對波峰幅值的影響較為顯著。

4 結(jié)論

精密慣性儀表內(nèi)部溫度場變化顯著, 在交變溫度載荷作用下, 螺紋連接結(jié)構(gòu)極易產(chǎn)生松動現(xiàn)象, 影響精密慣性儀表的精度及穩(wěn)定性。 本文基于機電阻抗檢測技術(shù), 針對溫度會影響精密慣性儀表螺紋連接狀態(tài)識別結(jié)果準確性的現(xiàn)象, 以粘貼了PZT 的半球型動壓氣浮軸承鎖緊螺母結(jié)構(gòu)為研究對象, 開展了溫度對PZT 信號的影響研究,通過仿真與試驗相結(jié)合的手段, 對溫度影響PZT阻抗信號的規(guī)律進行了探究, 得到的結(jié)論如下:

1）根據(jù)精密儀表服役時的溫度條件, 進行了仿真分析, 驗證了溫度對PZT 信號的影響規(guī)律。 溫度變化會顯著影響PZT 阻抗信號, 主要反映在信號峰值頻率和波峰幅值上。 隨著溫度的升高, PZT 阻抗信號的峰值頻率向左偏移, 而波峰幅值也會下降,且溫度對PZT 阻抗信號的影響也與頻率有關(guān)。

2）試驗結(jié)果表明, 在不同頻段內(nèi), 阻抗信號對溫度的敏感性不同。 溫度升高引起的峰值頻率偏移量隨著頻率的升高而增大, 波峰幅值的變化量隨著頻率的升高而下降。 在低頻范圍內(nèi), 波峰幅值對溫度的敏感性較高; 在高頻范圍內(nèi), 峰值頻率對溫度更加敏感。 根據(jù)溫度對PZT 阻抗信號的影響規(guī)律, 進一步進行溫度效應(yīng)的修正, 機電阻抗技術(shù)經(jīng)修正后可以對熱載荷下精密儀表的螺紋連接狀態(tài)進行準確識別。