火災環境下特高壓鋼管塔的最小安全距離研究

李聰聰，凌晨冰，孟祥俊偉，肖慶彪，馮立言，江文強

（華北電力大學 機械工程系，河北 保定 071003）

0 引言

利用特高壓輸電技術可以實現能源的遠距離、大容量輸送[1]。在研究輸電線路安全運行的影響因素時，不僅要考慮內部因素，如螺栓連接滑移[2]等，還要考慮外部因素。輸電線路所經過地區的極端氣候，如低溫[3]、覆冰[4]、強風[5]、火災[6]等，都有可能對特高壓輸電鐵塔造成破壞，影響輸電線路的正常運行。

鋼材是特高壓輸電塔的重要構成材料，其力學性能對輸電塔的安全性有顯著影響。當特高壓輸電塔遇到森林火災時，其鋼結構構件的屈服強度和彈性模量會在高溫下發生改變[7]；當構件溫度達到1 000 ℃以上時，鋼材的屈服強度只有常溫下的1/4，鋼結構幾乎喪失承載力。因此，有必要對特高壓輸電鐵塔在火災條件下的安全性問題開展研究[8]。

文獻[9]為了探究鋼結構在真實火災場景下的熱力響應，提出了 FDS-ABAQUS火熱結構耦合的分析方法。相較于傳統采用ISO834標準升溫曲線加載方式，模擬結構更接近真實火災場景下的結果。但是作者在文章中選用例證模型較為簡單，缺乏對復雜構件模型的驗證。

文獻[10]利用火災動態模擬器（Fire dynamics simulator，FDS）分析了大跨度鋼桁架拱橋在2種不同的火災場景下的溫度場分布，然后使用有限元軟件 ABAQUS分析了鋼桁架拱橋結構在不同火災場景下的力學性能的變化；但是，FDS與ABAQUS耦合數據為煙氣溫度，故結果精度較低。

文獻[11]分別利用 FDS和傳熱公式得到了機場航站樓屋頂鋼火災時局部構件的溫升曲線；然后使用有限元軟件計算了結構在設定的火災場景下的力學性能；給出了構件的失效標準。然而，此方法也存在計算結果精度低的問題。

文獻[12]開展了真實的火災時鋼構件的溫升實驗，構建了火災場景下大空間建筑鋼構件的理論溫升模型，提出了一種煙氣以及鋼構件溫度場的預測方法；通過實驗和理論結果數據對比，結合非規律變化的煙氣溫度場，驗證了預測方法的可行性。

文獻[13]為了研究鋼桁架結構在熱力耦合作用下的受力性能、鋼屋架的耐火能力，利用ABAQUS軟件進行了分析模擬實驗。結果表明：在火災下，該鋼屋架變形均在合理范圍內，最大應力也滿足結構安全性要求。但是，文中所采用的標準升溫曲線未能準確描述構件實際溫度變化情況。

為了反映真實森林火災環境下特高壓鋼管塔溫度場變化，本文利用FDS軟件模擬不同火災場景下鐵塔主要構件的溫度場；在此基礎上，計算得出火災時主材局部最大應力和屈服強度之間的關系；根據鐵塔的安全性要求，給出火災條件下特高壓鋼管塔的最小安全距離。

1 安全距離及判定

選取某典型特高壓鋼管塔主材為研究對象：主材一共分為8段，采用法蘭連接；每段為10 m，直徑為1.5 m；總高度為80 m。

以北方氣象條件為例，取特高壓鋼管塔工作環境為：海拔0 m，相對濕度20%，標準大氣壓。

1.1 分析流程

（1）火災時，鋼管塔主材溫度的獲得。使用FDS對不同的火災場景進行模擬；通過熱電偶分別獲取各火災場景下鋼管塔主材的最高溫度。

（2）主材屈服強度折減系數的計算。根據《建筑鋼結構防火技術規范》[14]，依據建筑規范中屈服強度的折減公式計算各火災場景下特高壓鋼管塔主材的屈服強度折減系數。

（3）鋼管塔安全距離的判定。根據主材的屈服強度折減系數，判定主材是否受到火場的影響，以及是否滿足強度設計標準。

1.2 判定依據

在火災中，當鋼結構達到一定溫度時，其屈服強度將發生變化。根據《建筑鋼結構防火技術規范》，高溫下普通鋼材屈服強度計算公式為

式中：fyT為溫度為Ts時鋼材的屈服強度，MPa；fy為常溫下鋼材的屈服強度，MPa；f為常溫下鋼材的強度設計值，MPa；Rγ為鋼構件抗力分項系數，這里取1.1；Tη為高溫下鋼材強度折減系數。

在設定火災場景時，本文綜合考慮了空氣濕度、大氣壓強、氧氣含量等環境因素；以此為基礎，探究大風工況下火源與主材距離關系。

2 火災場景仿真建模

2.1 模型簡化及火災場景設置

在所設定的仿真火災場景內，計算對象主要有火源、森林火場和特高壓鋼管塔主材，如圖1所示。圖1中，森林火場取4排5列有效區域。將實際樹木簡化為簡單的幾何模型后，以簡化后的幾何模型為基礎進行網格化[15]。

圖1 森林–鋼管塔主材火災場景設置Fig. 1 Fire scene setting of forest-main material of steel pipe tower

根據森林火場到主材距離d的不同設定六種火災場景，具體如表1所示。

表1 火災場景設定Tab. 1 Fire scene setup

2.2 網格敏感性分析

在進行數值模擬計算時，計算區域網格的尺寸將直接影響模擬計算的精度和收斂性。考慮過小的網格也會引起較大的計算誤差，因此：計算時，先使用粗糙的網格試運算；然后逐步將網格細化，直到前后2次模擬結果相近；最后，選擇其中一即可。

通過上述的網格敏感性分析，得到網格尺寸經驗值為火源特性直徑的 1/10。特征火焰直徑計算如式（4）所示。

式中：D*為網格尺寸；Q為火源熱釋放速率，kW；ρ∞為常溫下的空氣密度，kg/m3；T∞為環境絕對溫度，K；Cp為空氣的定壓比熱，J/(g·℃)；g為重力加速度，m/s2。

若整個計算區域采用統一網格，則網格數量會較多，進而影響計算速度。因此本文采用分塊網格：將整個區域分成森林火場區域、主材模型區域和煙氣羽流區域。前2個區域采用細網格，煙氣羽流區域采用粗網格。最后，將3個區域的網格按要求拼接。

2.3 探測裝置布置

為采集主材結構溫度以及周圍煙氣羽流溫度變化數據，根據表1繪制火災場景A1—A6的火災模型，并在主材表面和周圍設置熱電偶 T1—T8。圖2示出了火災場景模型及探測裝置分布。

圖2 火災場景及探測裝置分布Fig. 2 Schematic diagram of fire scene and distribution of detection devices

2.4 邊界條件及初始條件設定

常年平均風速設為5 m/s。

整個計算域共有6個面。將邊界左側面設為進風面。忽略土壤熱傳導，將邊界下表面設為絕熱壁面。邊界其余的面設為通風面。

當火災發生時，受計算域內外壓差的作用，高溫煙氣將從通風表面溢出，新鮮空氣將從通風表面補入[16]。

2.4.1 熱物理性參數及燃燒化學反應式

FDS反應庫中提供了多種物質燃燒反應，用戶也可以根據需要自定義反應。

在本文所研究的森林火災中，主要可燃物是木材，燃料方程式為：(C1.7O0.74N0.002)+1.021 21(O2+3.76N2)→1(0.964 384CO2+0.003 655CO+0.85H2O+0.0319 61C+3.840 76N2)。

背景氣體為氧氣和氮氣組成的空氣混合物。

燃燒時，木材與空氣發生反應，生成1.5%的煙氣和0.4%的CO。

特高壓鋼管塔材料設為Q345，密度為7 850 kg/m3，其在高溫下的熱物理參數如表2所示。

表2 特高壓鋼管塔材料的非線性熱物理參數Tab. 2 Non-linear thermophysical parameters of UHV steel tube tower materials

2.4.2 火源的熱釋放率以及樹木的熱解參數

在實際森林火災中，中等強度森林火災多發且蔓延范圍非常廣；所以，本文選取中等強度森林火災為模擬工況。

考慮計算條件，取小片有效森林區域作為火場區域，設置帶狀火源為：長15 m、寬0.5 m、熱釋放速率[17]為46 mW/m2。

火災蔓延的過程主要是材料熱解的過程。森林火災的蔓延，主要是樹冠燃燒蔓延。樹冠和樹干的熱物理和熱解參數[18]如表3所示。

表3 樹木的熱物理參數和熱解參數Tab. 3 Thermal physical parameters and pyrolysis parameters of trees

火源單位熱釋放率隨時間變化曲線如圖3所示。

圖3 火源單位熱釋放率曲線Fig. 3 Heat release rate curve of fire source

3 數值分析

3.1 森林火場與主材的熱作用

當森林火災發生時，森林火場和主材之間存在熱對流和熱輻射2種熱作用。

圖4示出了500 s時森林火場溫度等值面。圖4中，紅色等值面代表火焰層，其他均為煙氣層。

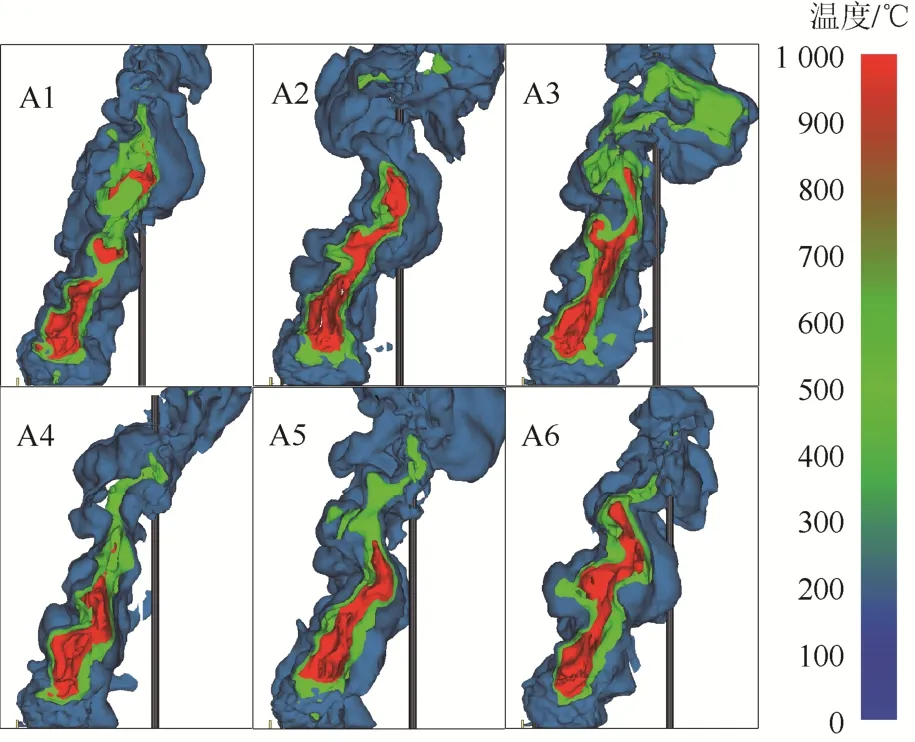
圖4 森林火場溫度等值面圖（t=500 s）Fig. 4 Isosurface map of forest fire field temperature

圖5示出了各火災場景主材熱輻射強度。

圖5 主材熱輻射強度Fig. 5 Thermal radiation intensity of main material

從圖5中可以看出：

對于A1、A2、A3和A5火災場景，在主材50 m高度以下的位置，熱輻射強度隨著高度的增加呈增大趨勢；50 m以上時，熱輻射強度迅速降低。

在A4和A6火災場景中，在主材60 m高度以下位置，主材鋼管熱輻射強度隨著高度的增加呈增大趨勢；60 m以上時，熱輻射強度迅速降低。

綜合考慮圖4、圖5可以得出：主材距離火場14 m～17 m時，熱輻射強度隨著主材距離火場距離增加逐漸減弱；主材距離火場13 m時，主材受到熱輻射強度最大，為 242 kW/m2。對于各火災場景，在主材高度0～50 m區間段，主材受到熱輻射作用逐漸上升；60 m～80 m區間，主材熱輻射作用減弱。主材所受熱輻射強度最強位置為50 m附近。

3.2 主材溫度變化趨勢

主材不僅會受到森林火場熱對流和熱輻射作用，主材各部分也會進行熱傳導。森林火場與主材之間距離的不同，主材溫度分布也會隨之發生改變。

火災高峰時的主材溫度分布如圖6所示。各場景下鋼管塔主材各測點溫度分布如圖7所示。

圖6 火災高峰時主材溫度分布規律Fig. 6 Temperature distribution law of the main material during fire peak

圖7 各火災場景主材最高溫度Fig. 7 Maximum main material temperature of each fire scene

從圖6可以看出：A1—A3火災場景下，主材最高溫度為420 ℃。A4—A6火災場景下，最高溫度為220 ℃，并且主材溫度均呈中間高、兩邊底分布規律；隨著距離增大，高溫區呈逐漸減小的趨勢。

從圖7中可以看出：對于A1—A5火災場景，當主材距離火場分別為12 m、13 m、14 m、15 m、16 m，主材50 m高度以下時，主材鋼管溫度隨著高度的增加呈增大趨勢；超過50 m后，溫度迅速降低。以A1火災場景為例，主材鋼管溫度從開始的313 ℃逐漸增大到566 ℃；之后隨著高度的增大迅速下降到123 ℃。A2—A5火災場景與A1場景變化規律基本類似。對于A6火災場景，當主材距離火場為 17 m時，主材鋼管溫度從開始的252 ℃逐漸增大到267 ℃，之后隨著高度的增大迅速下降到143 ℃。由此可見，隨著主材與火場距離的增加，主材最高溫度不斷降低，主材距離火場12 m時，主材的溫度峰值最大，溫度值為568 ℃。對于各火災場景，在主材高度0～50 m區間段，溫度逐漸上升；在50 m～80 m之間時，主材溫度迅速下降。主材最高溫度峰值均位于50 m附近。

3.3 鋼管塔主材安全距離判定

考慮到輸電鐵塔在設計時，其主材構件強度利用率一般均在0.9左右，所以本文以“屈服強度折減系數在0.9以下”作為主材失效的判定準則。

利用式（2）計算屈服強度折減系數。折減系數等于1，說明主材沒有受到高溫影響；折減系數小于1且大于0.9，說明主材屈服強度發生變化，但是滿足強度設計要求；折減系數小于0.9，說明主材局部可能發生屈服變形失效。

圖8示出了主材于不同高度的屈服強度折減系數計算結果。從圖8可以看出，在不同火災場景下，最小屈服強度折減系數出現位置基本相同：最小值均出現在50 m高度附近。因此，主材距離地面50 m高度是有可能最先發生失效的位置。

圖8 主材于不同高度屈服強度折減系數Fig. 8 Reduction coefficient of yield strength of different heights

圖9示出了不同火災場景下，主材最大屈服強度折減系數計算結果。從圖9中可以看出：隨著主材與火場距離的增大，其屈服強度折減系數也逐漸增大。主材距離火場12 m～14 m時，主材的屈服折減系數分別為0.54、0.64、0.88；15 m～17 m時，主材的屈服折減系數分別為0.93、0.99、1。由此可見，主材距離火場12 m～14 m時，主材局部可能會發生屈服變形失效；15 m～16 m時，主材雖然滿足使用標準，但是受到高溫影響屈服強度發生折減，力學性能發生改變；17 m時，主材強度在高溫作用下和無火作用相比沒有變化。綜上所述，15 m為最小安全距離。

圖9 不同火場距離下屈服強度折減系數Fig. 9 Reduction coefficient of yield strength at different fire distances

4 結論

本文通過仿真建模，研究了在森林火場與主材不同距離條件下，特高壓鋼管塔機械強度變化情況，得到結論如下。

（1）當主材距離火場12 m、13 m、14 m、15 m時，其屈服強度分別下降了46%、36%、12%、7%。在主材距火場由14 m過渡到13 m的過程中，屈服強度下降變化幅度較大。

（2）對于各火災場景，主材溫度的變化趨勢相同：在主材50 m高度以下位置，主材鋼管溫度隨著高度的增加呈增大趨勢；超過50 m后，溫度迅速降低，在40 m～50 m之間取得峰值。

（3）當主材與火場距離在14 m以內時，主材局部會發生屈服變形失效，失效位置位于距離地面50 m高度附近；距離大于15 m時，受到高溫影響，材料屈服強度會發生折減，但仍滿足標準要求。故最小安全距離為15 m。