基于多周期性MILP模型的新型配電系統拓撲辨識方法

蕭展輝，鄒文景，唐良運

(南方電網數字電網研究院有限公司，廣州 510000)

0 引 言

新型配電系統是深度融合了分布式能源、柔性負荷、新型儲能、柔性多狀態開關等設備的復雜系統[1-2]，其結構更趨復雜、潮流分布極不確定、調控節點更加細密。配電系統的狀態估計、故障定位、電壓/無功控制等功能的實現都嚴重依賴于準確的拓撲結構，因此，拓撲辨識(Topology Identification, TI)[3]對于新型配電系統的運行控制至關重要。然而，在實際工程中，由于配電系統的測量數據有限、配電饋線上開關和斷路器的狀態信息不可用、不可靠，使得準確辨識配電系統的拓撲結構十分困難。

在實際工程中最常用的拓撲辨識方法是配電網運維人員現場查看饋線上開關和斷路器的開斷狀態，這種做法雖然簡單可靠，但不能持續地跟蹤配電系統拓撲結構的變化。因此，基于量測的拓撲辨識方法根據傳感器的測量數據來估計饋線上開關和斷路器的狀態[4-5]。文獻[6]基于匹配環路功率確定可能的拓撲結構,并根據公共量測值對可能的拓撲結構進行狀態估計。文獻[7]基于支路有功功率殘值的大小選擇可能斷開的支路，得到若干種可能拓撲結構,在每個可能拓撲結構下分別進行狀態估計。文獻[6-7]中的拓撲辨識方法主要是根據傳感器量測數據對可能的拓撲結構進行狀態估計，在狀態估計中根據最小殘差來選擇拓撲結構。然而，這類基于狀態估計的拓撲辨識方法需要足夠的量測數據來提高狀態估計的準確性，這對于分支眾多的配電系統來說，安裝足夠多的傳感器去獲取量測數據顯然不可取。為此，也有文獻采用有限的量測數據來實現拓撲辨識。文獻[8]通過對電壓序列的動態時間彎曲距離進行聚類分析，自動識別低壓用戶所屬臺區，得到正確的低壓配電臺區網絡拓撲結構。文獻[9]通過在每類臺區內采用Tanimoto相似度系數計算各臺區內設備的相似性及隸屬關系，從而實現相關臺區的拓撲辨識。文獻[10]用皮爾遜相關系數判斷用戶電壓序列曲線的相似性，通過相關系數算法來辨識臺區戶變關系。但這類拓撲辨識方法也需要積累一定數量的電壓樣本，存在辨識分辨率不高、計算量大等問題。

隨著大數據以及配電系統高級量測體系技術的發展，已有文獻從各臺區的電壓、電流的時空特性數據挖掘出隸屬關系，實現拓撲辨識。文獻[11]通過建立基于KCL的優化模型，并將其轉化為二次規劃問題求解，實現低壓配電網線戶關系識別。為了克服數據缺失問題，文獻[12]利用知識圖譜技術對多個低壓配電網信息系統中的數據進行整合，推理出缺失數據，挖掘出各數據之間的關聯建立拓撲結構。文獻[13]建立了基于節點多時段有功、無功負荷和電壓幅值量測的非線性參數估計模型，提出了配電網拓撲重建算法。文獻[14]提出了一種配變互聯關系辨識的集成深度神經網絡模型，提高了靈活網絡的拓撲辨識精確度。文獻[15]利用支持向量機多分類模型來辨識量測數據所對應的拓撲。可見這些拓撲辨識方法均是通過數據重構拓撲，缺乏內在的機理解釋，對數據的糾錯能力有限[16-17]。

從上述文獻也可以看出，考慮測量電流的拓撲辨識方法的數據容錯能力有待提升。隨著新型配電系統饋線終端FTU上升級改造之后配置寬帶電壓傳感器、寬帶電流傳感器。與測量電壓和功率的傳感器相比，寬帶電流傳感器的成本更低且更易于安裝，非接觸式電流傳感器還可以測量電場，可用于估計當前測量的相對相位角。換句話說，這些電流傳感器可以估計相量，就像u-PMU[18]。為此，文中提出一種基于支路電流的配電網拓撲辨識方法。在構建基于支路電流測量的背景下，建立了拓撲辨識的多周期性混合整數線性優化模型，提高了拓撲辨識的精度和魯棒性，IEEE-33節點系統的仿真測試驗證了文章方法的優勢。

1 基于支路電流的新型配電系統拓撲辨識

1.1 拓撲辨識的MINLP模型

假設配電系統中所有線路的開關處于閉合狀態。根據基爾霍夫電流定律(KCL)，注入每個節點的電流等于與該節點相連接的線路的支路電流總和：

(1)

式中Ii為節點i的注入電流；Iij為線路(i,j)的支路電流；Ni為與節點i相連接的節點集合；N為配電系統所有節點。

線路(i,j)流過的支路電流Iij取決于線路的開關狀態、兩個節點的電壓以及線路的導納。根據基爾霍夫電壓定律(KVL)，可得：

Iij=sij(Vi-Vj)yij

(2)

式中sij表示線路(i,j)的運行狀態，sij為1表示在運行；否則為0，保證Iij為0；Vi、Vj分別表示節點i、j的節點電壓；yij為線路(i,j)的導納。

根據節點電壓Vi和節點注入電流Ii，可以得到節點注入功率：

(3)

式中Si表示節點i的負荷注入功率；bi表示節點i與系統的連接狀態，如果節點i連接到網格，則bi為1；否則為零，表示存在孤島節點。在這種情況下，拓撲辨識方法可以確定停電區域；從而將其擴展到基本拓撲辨識，形成拓撲辨識問題的優化模型：

(4)

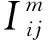
1.2 拓撲辨識的MILP模型

拓撲辨識的MINLP模型式(4)是一個典型的混合整數非線性優化問題，本節將此模型轉換為更易于求解的MILP模型。

式(2)中的非線性是由于0-1變量sij與連續相量變量Vi和Vj的乘積。為了消去這種非線性，將式(2)代入以下線性方程：

Iij=yijUij

(5)

式中Uij為一個輔助變量，相當于sij和Vi-Vj的乘積。如果sij=1，即如果線路(i,j)處于閉合狀態，則Uij=Vi-Vj，否則Uij=0。Uij、sij和Vi-Vj之間的上述關系可以通過添加以下線性約束來消去非線性項[19]：

-M(1-sij)≤Re{Uij}-Re{Vi-Vj}≤M(1-sij)

(6)

-Msij≤Re{Uij}≤Msij

(7)

-M(1-sij)≤Im{Uij}-Im{Vi-Vj}≤M(1-sij)

(8)

-Msij≤Im{Uij}≤Msij

(9)

因為Uij和Vi-Vj是復數變量，所以式(6)～式(9)中的方程分別采用Re和Im取實部和虛部。如果sij=0，則約束條件式(6)和式(8)不起作用；從約束條件式(7)和式(9)中可得到Uij=0，同時Iij=0。因此，當sij=0時，強制執行式(2)中的非線性等式約束。如果sij=1，則約束條件式(7)和式(9)不起作用；從約束條件式(6)和式(8)中可以得到Uij=Vi-Vj，因此有Iij=(Vi-Vj)yij。因此式(2)中的非線性等式約束也在sij=1時強制約束，式(5)～式(9)中的線性約束等價于式(2)中的非線性約束。

拓撲辨識的MINLP模型式(4)的另一個非線性項是約束條件式(3)中相量Vi和Ii的乘積，即非線性潮流約束。非線性潮流約束的線性化方法很多，但需要適應不同的拓撲結構，而且分支電流必須保留。為此，采用文獻[20]中的線性化方法，該方法基于復數域的泰勒展開，而不是在實數域的潮流方程進行泰勒展開。假設節點i的電壓在額定電壓1 pu附近，可以表示為：

Vi=1-ΔVi

(10)

通過應用泰勒級數并忽略高階項，可得到：

(11)

這種復數域的泰勒展開近似的精度可以通過潮流解來進行驗證，其近似誤差為：

(12)

在文獻[20]中繪制出了誤差指標如圖1所示。

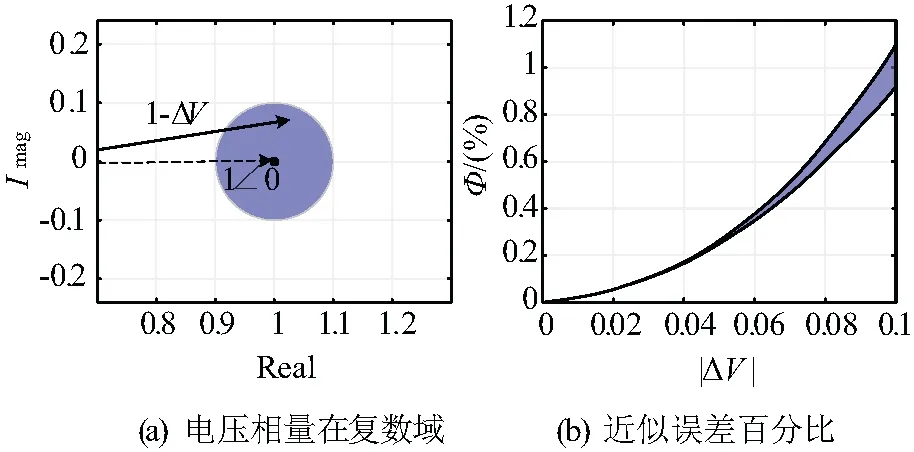
圖1 驗證式(11)中線性化的準確性：Fig.1 Validating the accuracy of the linearization in formula(11)

圖1(a)為以1.0為圓心，在ΔVi為半徑的圓盤內的每個點進行評估，得到圖1(b)中的誤差區域。例如，在ΔV=0.1 p.u.時，近似誤差僅為1%左右。實際中ΔV通常小于0.05 p.u.，因此，逼近誤差小于0.3%，這是滿足工程潮流計算的精度要求。

將式(11)代入式(3)可得：

(13)

然而，由于0-1變量bi和相量變量Vi相乘，上述方程仍然是非線性的。因此，引入一個新的輔助變量Wi， 將式(13)替換為如下線性方程：

(14)

式中Wi等價于bi和Vi的乘積。如果bi為1，即如果節點i連接到系統，則Wi=Vi；否則Wi=0，表示該節點未連接到系統。Wi、bi和Vi之間的上述關系可以通過增加如下線性約束來實現：

-M(1-bi)≤Re{Wi}-Re{Vi}≤M(1-bi)

(15)

-Mbi≤Re{Wi}≤Mbi

(16)

-M(1-bi)≤Im{Wi}-Im{Vi}≤M(1-bi)

(17)

-Mbi≤Im{Wi}≤Mbi

(18)

上述Big-M的方法與式(6)～式(9)的原理基本一樣，這里不在贅述。

需要注意的是，式(14)可以保證斷開節點的注入電流為零，但不能保證斷開節點的電壓也為零，因此，還需要添加一組新約束，以確保斷開節點的電壓為零，即：

-Mbi≤Re{Vi}≤Mbi

(19)

-Mbi≤Im{Vi}≤Mbi

(20)

(21)

(22)

Eij≥0 andFij≥0

(23)

綜上所述，拓撲辨識的MINLP模型轉化為如下的MILP模型：

(24)

滿足式(1)、式(5)～(9)、式(14)～式(23)。

2 考慮偽測量和周期的拓撲辨識方法

2.1 電流傳感器的優化配置

從理論上講，為了辨識配電系統的拓撲結構，每條支路均配置電流傳感器，這會造成巨大的投資成本，為此，電流傳感器優化配置是為了解決支路電流的可觀測性，以便有足夠的支路電流數據支撐拓撲辨識的MILP模型。電流傳感器優化配置就是明確支路電流傳感器的配置支路和數目，從而實現配電系統支路電流的可觀測性，從而準確地辨識拓撲。文章證明了配電系統支路電流可觀測性的必要條件是在配電系統的每個獨立回路中至少配置一個電流傳感器，則配電系統的拓撲是可以準確辨識的。證明過程如下：

證明：一個電路中有N個節點和L條支路，則需要L個獨立方程來獲取支路電流。從N個節點的注入電流方程中，N-1個方程是獨立的[21]。因此，為了獲取L個獨立的支路電流方程，需要L-(N-1)個額外的獨立方程，因此，通過測量L-(N-1)條支路電流來獲得獨立方程。

回路是從一個節點開始，經過一組節點后，返回到初始起始節點的閉合路徑，且一個至多經過一次。如果一個回路本身不包含任何回路，則稱該回路是獨立的。在電路理論中，獨立回路產生獨立的KVL方程。因此，只需要電流傳感器測量到獨立回路中的L-(N-1)條支路電流，就可以推算出所有支路電流。

對如圖2所示的一個獨立的回路，假設節點注入電流為I1,I2,...,In已知，要得到回路中每條支路的電流，In,1,I1,2,...,In-1,n，根據KCL可得：

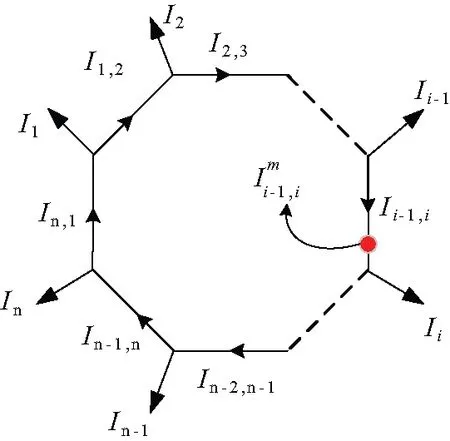
圖2 n個節點組成的獨立回路，電流傳感器配置在支路{i-1,i}以測量Fig.2 An independent loop consisting of n nodes, the current sensor is installed at branch {i-1,i}

(25)

(26)

與式(25)不同，式(26)具有唯一解。因此可以得出在獨立回路中的任意支路配置一個支路電流傳感器，就可以附加一個獨立方程到回路的KCL方程中。由于網絡中有L-(N-1)個獨立回路；在每個獨立回路配置L-(N-1)個支路電流傳感器，為可以推算出所有支路電流。

接下來用簡單的電路例子來說明配電系統支路電流可觀測性的必要條件。如圖3所示。

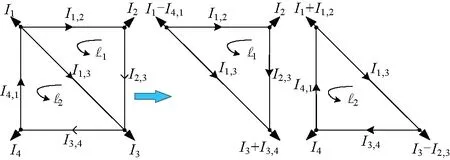
圖3 由4個節點和2個回路組成的電路Fig.3 A circuit with 4 nodes and 2 loops

在節點數N=4、支路L=5的電路中，用l1表示的回路1231和用l2表示的回路1341是兩個獨立回路。需要注意的是回路12341不是一個獨立回路，因為它在其內部包含其他回路l1或l2。則該網絡的KCL方程組如下：

(27)

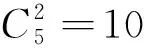
表1 圖3中網絡的電流傳感器配置方案Tab.1 Current sensor configuration scheme of the network in Fig.3

2.2 考慮偽測量誤差的拓撲辨識方法

為了解決測量和偽測量中誤差的影響，將式(1)中的注入電流約束以懲罰項的形式添加到目標函數中，有：

(28)

通過采用與第1.2節中類似的方法將式(28)的絕對值線性化處理，定義輔助變量Gi和Hi， 并增加以下線性約束條件：

(29)

(30)

Gi≥0，Hi≥0

(31)

考慮測量和偽測量中誤差的拓撲辨識的MILP模型進一步改寫為：

(32)

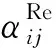
2.3 考慮測量周期性的拓撲辨識多周期優化方法

式(32)中拓撲辨識的MILP模型是針對單個時間周期的，在實際中，支路電流測量值可能在配電系統拓撲變化后的初始時刻繼續采用。拓撲辨識需要考慮測量的多周期性問題，以更好地減輕測量誤差和偽測量的影響。T表示測量和偽測量的周期數，[t]表示每個時刻t對應的數據，t=1…T，讓Ψ[t]表示在t時刻式(32)中的目標函數。因此，考慮測量周期性的拓撲辨識MILP模型表示為：

(33)

滿足式(5)～式(9)at[t],t=1,…,T,式(14)～式(23)at[t],t=1,…,T,式(29)～式(31)at[t],t=1,…,T。

式(33)可以看成是基于多場景的優化模型，其中γ[t]表示與場景t相關的概率。如果不同場景的隨機性服從均勻分布，則可以選擇γ[t]=1/T,?t=1,...,T；否則，可以使用已知的非均勻概率分布。這是由于每個節點負荷存在隨機性，測量值和偽測量值會隨機變化，每個場景都會為這些隨機負荷變量生成一個新的隨機場景，在估計開關狀態時提供冗余。

3 仿真分析

采用IEEE-33節點標準算例來驗證所提出的拓撲辨識方法，接線示意圖如圖4所示，所有支路開關的狀態采用實線和虛線表示，常閉合開關用實線表示，常開開關用虛線表示。圖4中由標記為l1～l5的五個回路組成，支路電流傳感器配置在支路在<8>、<13>、<20>、<24>和<29>上。由于該配電系統中有21個開關，因此可以創建221種不同的拓撲，其中選擇了65種拓撲配置，包括50個輻射狀、10個回路和5個孤島。除了電流測量之外，假設所有負荷注入都可以通過偽測量獲得。

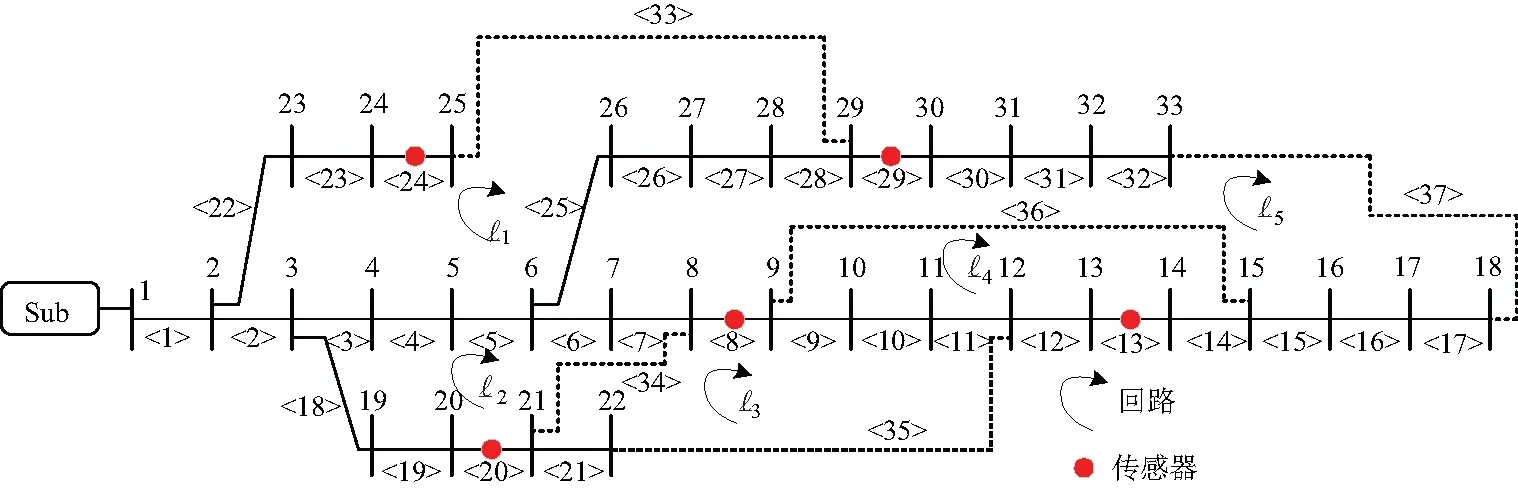
圖4 IEEE-33節點測試系統Fig.4 IEEE-33 node test system

本節的拓撲辨識算法在Matlab軟件中實現，并調用intlinprog函數求解式(24)、式(32)和式(33)中的MILP模型。在仿真中：

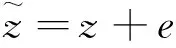
(34)

(35)

這保證了99.7%的ei值落在真實值的±ηi百分比范圍內。此外，拓撲辨識方法的精度定義如下：

(36)

在實際中，偽測量通常是基于智能電表數據或歷史數據的短期負荷預測獲得的，采用蒙特卡羅方法生成不同的場景，針對任何給定的測量不準確度驗證文所提出的拓撲辨識算法的魯棒性。

在仿真測試中假設偽測量誤差在10%～50%的范圍內，評估所提出的拓撲辨識算法在不同偽測量誤差下的精度。表2給出了在不同偽測量誤差下的拓撲辨識精度。不難看出：如果偽測量誤差低于30%，拓撲辨識精度高達98%左右，隨著偽測量誤差增加到50%，那么拓撲辨識精度會顯著下降；使得拓撲辨識結果不可靠。當然，在如此高的偽測量誤差下，失去拓撲辨識精度也是不可避免的。

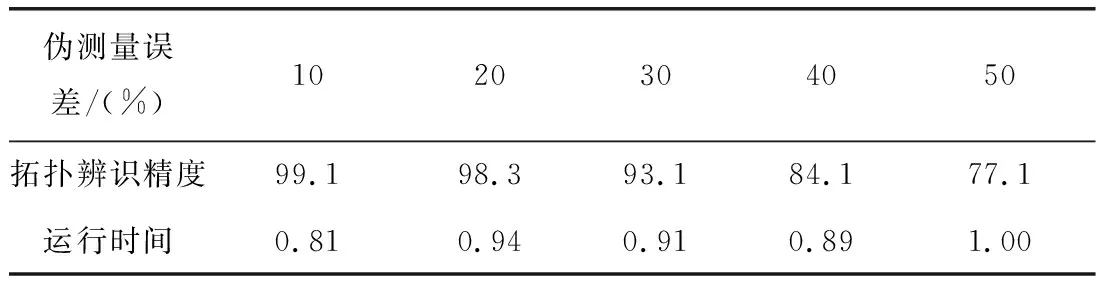
表2 在不同偽測量誤差下的拓撲辨識精度Tab.2 Topology identification accuracy under different pseudo measurement errors

偽測量中誤差的影響可以通過2.3節所提出的拓撲辨識多周期優化方法補償。為了測試拓撲辨識多周期優化方法的性能，采用正態概率分布生成偽測量誤差，均值為零，標準偏差為式(35)，求解式(33)中的拓撲辨識的多周期優化模型，每次新的測量場景都可用于更新辨識結果。

圖5給出了不同偽測量誤差下的拓撲辨識多周期優化方法的精度。隨著更多測量場景的增加，拓撲辨識精度逐漸增加。即使偽測量誤差達到50%，拓撲辨識單周期優化方法的準確度為77.1%，而多周期優化方法在增加20個測量場景后將準確度提高到了95.0%。當然，求解式(33)中的拓撲辨識的多周期優化模型的計算復雜度隨著場景數量的增加逐漸增大，拓撲辨識的多周期優化方法運行10個和20個場景分別需要大約40 s和125 s，這比表2中給出的單周期優化方法運行時間要長得多。

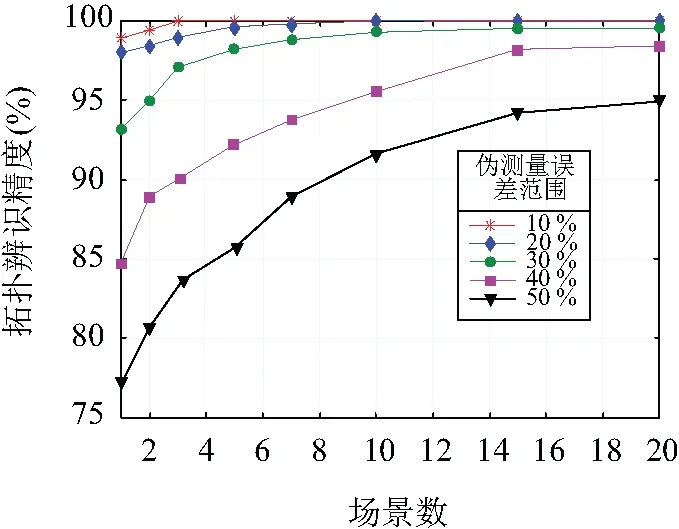
圖5 IEEE-33節點測試系統Fig.5 IEEE-33 node test system

進一步，對比了拓撲辨識的多周期優化方法和單周期優化方法，拓撲辨識結果如表3所示，表3中×表示拓撲辨識錯誤，√表示拓撲辨識正確，在仿真中，IEEE-33節點配電系統拓撲在所有15個場景中保持不變。從表3中看出，拓撲辨識的單周期優化方法僅能辨識出場景6、場景9、場景11和場景13這四個場景的拓撲，其他11個場景的拓撲都辨識錯誤，這是由于負荷變化和偽測量誤差較大而引發的。然而，拓撲辨識的單周期優化方法只要有足夠的場景6個就能辨識正確的拓撲。拓撲辨識的多周期優化方法在僅有第一個場景時與拓撲辨識的單周期優化方法相同，在獲取第2個場景后，拓撲辨識的多周期優化方法就可以利用第一個和第二個測量場景的組合，依此類推。

表3 拓撲辨識多周期優化方法和單周期優化方法的比較Tab.3 Comparison between multi-period optimization method and single-period optimization method for topology identification

進一步與文獻[22]中提出拓撲辨識的MIQP模型進行對比，結果如表4所示，不難發現：文中所提出的拓撲辨識MILP模型比文獻[22]中的MIQP模型精度更高，能夠削弱偽測量誤差造成的拓撲辨識影響。這是因為文獻[22]中的MIQP模型中的目標函數的平方和將偏離期望值，而不是像文中最小化絕對誤差。此外，MIQP的計算時間比MILP多。從成本效益的角度來看，文獻[22]中的MIQP方法需要采用10個支路功率傳感器，而文中僅需采用5個支路電流傳感器，這也證明了文中方法簡單、成本效益高等優勢。

表4 文中方法與MIQP模型的比較Tab.4 Comparison between the proposed method and MIQP model

最后，針對支路電流傳感器測量誤差和偽測量誤差共同作用下驗證所提出的拓撲辨識方法的性能，這里支路電流測量誤差以總矢量誤差表示，包括幅度誤差和角度誤差，拓撲辨識結果如表5所示。從表5可以看出，所提出的拓撲辨識方法受偽測量誤差的影響比支路電流測量誤差更大。當然，這里認為偽測量的誤差要高得多，因為在實際中確實如此。

表5 支路電流傳感器測量誤差和偽測量誤差共同作用下的拓撲辨識精度Tab.5 Topology identification accuracy under the branch current sensor measurement error and pseudo measurement error

4 結束語

在新興的非接觸式、低成本的電流傳感器的基礎上，提出了配電系統拓撲辨識的多周期性混合整數線性優化模型，IEEE-33節點系統的仿真測試結果表明：

(1)如果偽測量誤差低于30%，拓撲辨識精度高達98%左右，隨著偽測量誤差增加到50%，那么拓撲辨識精度會顯著下降,使得拓撲辨識結果不可靠；

(2)隨著更多測量場景的增加，拓撲辨識精度逐漸增加。即使偽測量誤差達到50%，拓撲辨識單周期優化方法的準確度為77.1%，而多周期性優化方法在增加20個測量場景后將準確度提高到了95.0%;

(3)偽測量誤差對所提出的拓撲辨識方法的精度影響較支路電流測量誤差更大。