新型半潛式浮式風機在不同流速下的動力響應特性研究

2023-03-01 09:31:02樂叢歡張浦陽丁紅巖

船舶力學 2023年2期

樂叢歡，李闊，張浦陽，丁紅巖

（天津大學 a.水利工程仿真與安全國家重點實驗室；b.建筑工程學院，天津 300350）

0 引言

海洋風能是一種清潔、無污染的可再生能源，因其風速大、切變小、主導風向穩定等優點受到世界各國的廣泛關注，是新能源中最具開發條件和最有發展前景的發電方式之一。隨著近海風資源逐漸枯竭，海上風電從近海走向深遠海將是必然的趨勢。當水深超過50 m 時，固定式基礎的建造、施工費用將變得十分昂貴，浮式風機為深遠海風能的開發提供了一種可行的方案。浮式風機的發展廣泛借鑒了海上油氣勘探平臺的經驗，但浮式風機系統結構也顯著區別于傳統的海洋平臺，在實際海域的運行中，由于其復雜的結構、環境荷載與耦合效應，使得浮式風機的研究成為一項具有挑戰性的工作。目前主流的浮式風機基礎型式主要包括三種類型：單立柱（Spar）式、半潛式（Semi-submersible）和張力腿平臺式（TLP）[1-2]。其中半潛式基礎是目前技術最為成熟、最具商業開發價值的基礎形式，其特點是可在陸上建造、組裝、調試，由于大水線面具備海上自浮拖航條件，具有較大機動性，利用水線面提供回復力矩保持穩性，適用水深范圍廣，且運行可靠，可以在沒有錨鏈的情況下在水中漂浮，常采用懸鏈式系泊系統來約束風機系統水平方向上的位移，施工方便。但半潛式基礎體型一般較大，建造所需的材料比較多，受到的波浪載荷較大，垂蕩響應是半潛式基礎設計中最為突出的問題[3]。

近年來國內外專家學者針對半潛式浮式風機開展了一系列研究，提出了各種不同形式的半潛式基礎。Cermelli 等[4]的研究證明，三角形的半潛式平臺具有較好的性能。2010 年，Principle Power 公司設計了一種名為WindFloat的5 MW 半潛式浮式風機，其中半潛式平臺為3立柱結構，風機安裝在其中一個立柱上，采用主動壓載調節系統，可根據浮式平臺的實時姿態進行壓載水調節，保證浮式風機的穩性。Roddier 等[5]通過數值模擬和水池試驗的方法研究WindFloat 半潛式風機的動力特性，并對水平支撐桿件的強度和疲勞進行了評估。2020 年3 月，WindFloat Atlantic 風場成功應用WindFloat 安裝了一臺MHI Vestas 8.4 MW 風機實現了并網發電。Robertson 等[6]提出了一種3立柱式OC4-DeepCwind 半潛式風機，對其水動力特性進行研究，與WindFloat 不同的是，OC4-DeepCwind 風機由中心柱支撐。Bayati等[7]以OC4-DeepCwind半潛式風機為研究對象，基于FAST軟件研究了二階水動力對OC4-Deep-Cwind半潛式風機的影響，結果表明，二階差頻力能夠激發平臺更大的響應，在惡劣海況下二階差頻力的計算是必要的。浮式風機系統是一個高度耦合的復雜動態系統，其動力學模型需要考慮風機氣動荷載、浮式平臺水動荷載、結構彈性、風機控制策略和系泊系統等耦合作用，研究涉及水動力學、空氣動力學、結構力學及控制系統等多學科交叉，目前半潛式浮式風機的研究主要集中在新型浮式風機概念設計以解決目前浮式風機成本過高的問題、基于數值和模型試驗的方法對其技術可行性的論證等方面。數值和模型試驗研究多考慮風、浪或風浪聯合作用對浮式風機的影響，基本上未考慮海流的作用。而通常海域表面海流流速大，加上半潛式基礎水線面積大的特點，忽視海流作用勢必會引起風機動力響應的誤差。本文針對50～120 m的中等水深海域，設計了一種新型3立柱式半潛式浮式風機，針對WindFloat 和OC4-DeepCwind 基礎采用桁架式結構連接、連接節點多、建造加工不便且結構疲勞敏感性高的缺點，新型半潛式浮式風機采用無支撐結構。為進一步降低建造成本，基礎主體采用高強輕質混凝土材料，與鋼結構相比，具有更好的抗疲勞和抗腐蝕的性能。本文以新型半潛式浮式風機為研究對象，采用數值模擬的方法，用頻域法研究浮式平臺的水動力特性，并進一步建立風機-塔筒-浮式平臺-系泊系統的耦合數值模型，考慮二階差頻波浪力作用，對新型半潛式風機開展風、浪、流共同作用下時域分析，重點分析海流對新型半潛式浮式風機動力性能的影響。

1 概念設計

新型半潛式浮式風機的風電機組和塔筒選用美國可再生能源實驗室（NREL）為研究浮式風機而開發的5 MW 水平軸風機[8]，額定風速11.4 m/s，采用變速變槳控制。半潛式浮式基礎主要由中心立柱、三個邊柱、三個水平浮筒以及垂蕩板組成，如圖1 所示。中心立柱用于連接上部塔筒、機組，邊柱裝載壓載水，調節平臺吃水。基礎主體采用高強輕質混凝土材料，密度為1900 kg/m3，浮式風機的運行水深為100 m，根據設計海況和風電機組參數，經過初步的一體化設計確定的新型半潛式風機主要參數如表1 所示，基礎設計吃水22.4 m，排水量13 415.8 m3。其中邊柱直徑12 m，水面以上部分高12 m；下部垂蕩板厚0.4 m，邊長12 m，起到減小浮式風機垂蕩響應的作用。通過6 根懸鏈線錨鏈錨泊于海底，錨鏈呈對稱布置，分為三組，同組的2 根錨鏈間水平投影夾角為30°，選取公稱直徑為90 mm 的R4級錨鏈[9]，預張力1000 kN。

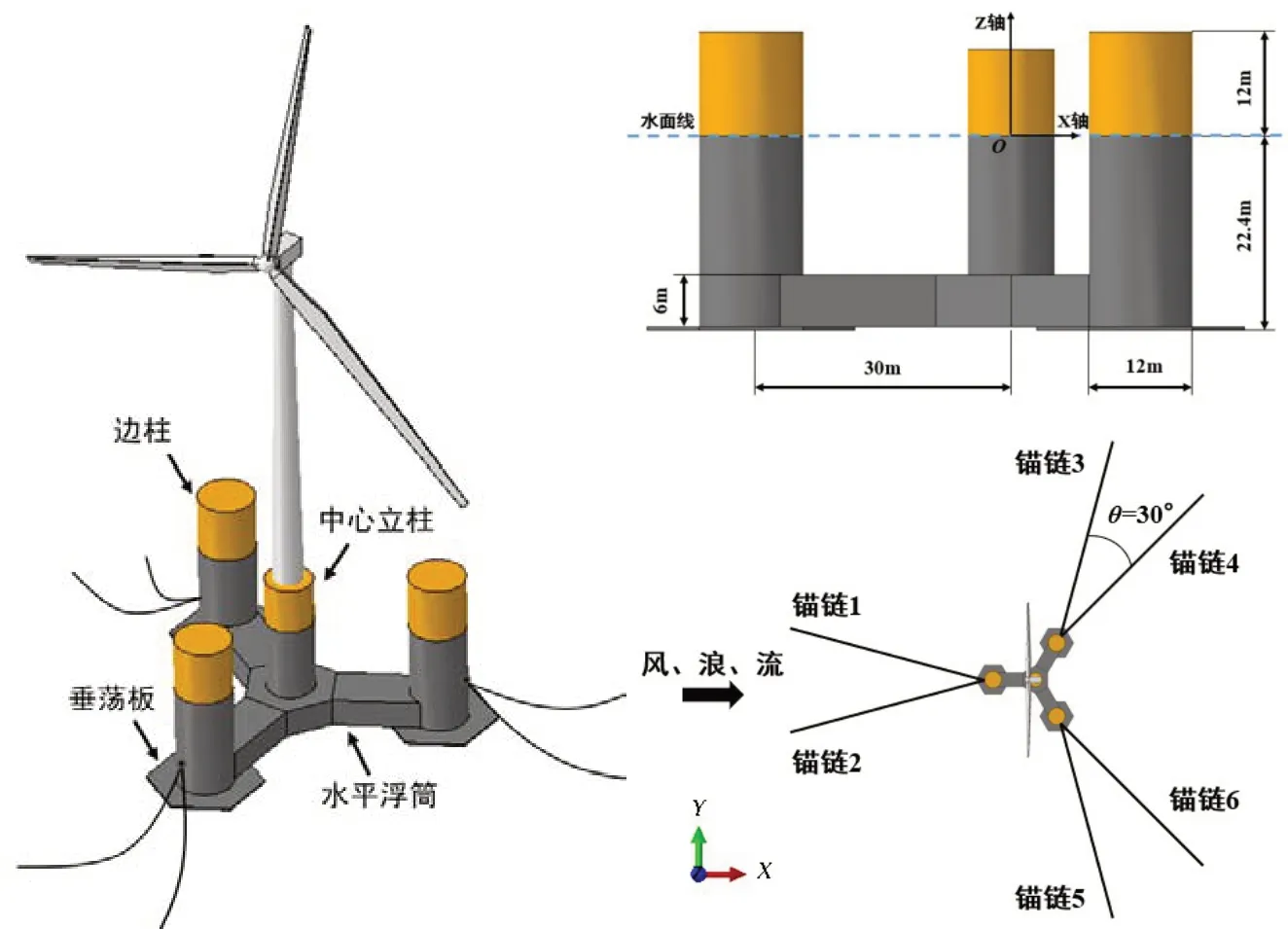
圖1 新型半潛式浮式風機基礎Fig.1 Foundation of new semi-submersible floating wind turbine

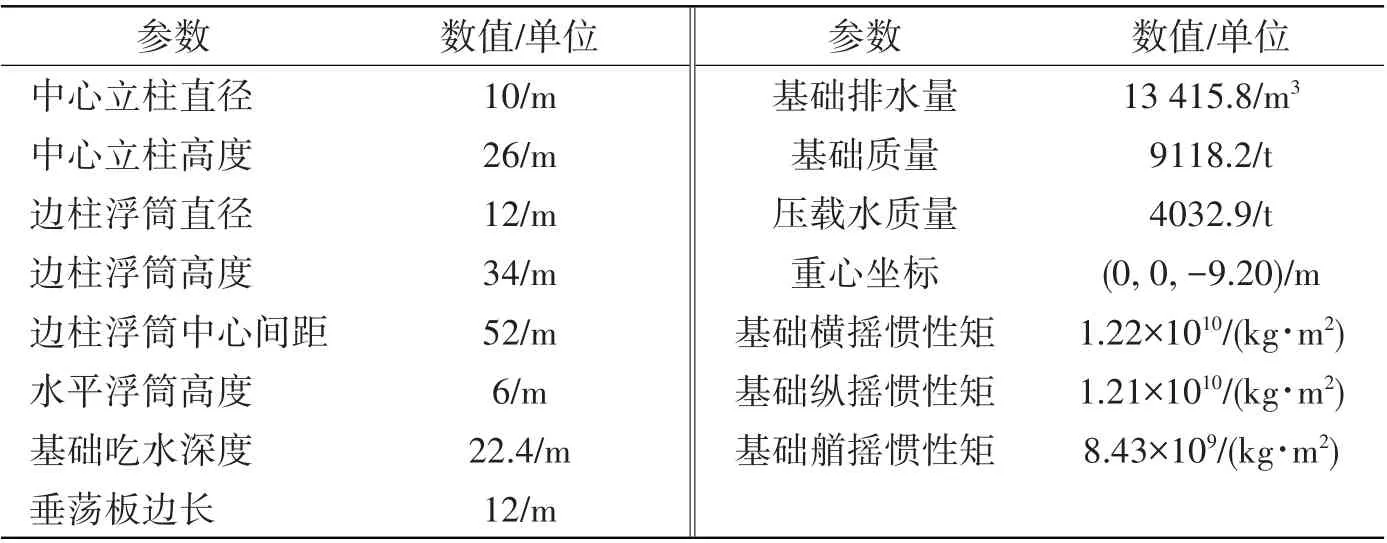
表1 新型半潛式風機基礎主要參數Tab.1 Main parameters of new semi-submersible foundation

2 全耦合模型建立

2.1 耦合運動方程

半潛式浮式風機是一個由葉片-機艙、塔筒、半潛式浮式平臺及系泊系統組成的復雜多體系統。風機運行過程中受到氣動載荷、浪和流等水動力載荷、系泊載荷等作用，其運動方程可以表示為

2.2 氣動載荷

風荷載的計算包括兩部分，一部分是風作用于風輪產生的氣動載荷，另一部分是風作用于靜水面以上浮式平臺和塔筒的推力。風機正常運行時，塔筒所受風載荷相較風輪所受風載荷小一個量級，但當風機順槳停機時，塔柱的風荷載則是風荷載的主要部分，根據CCS規范其計算的表達式為[10]

式中，Ch為高度系數，Cs為形狀系數，Si為第i個受風構件的正投影面積，V為設計風速。

風輪氣動載荷計算是基于葉素動量理論（BEM）[11]。葉素動量理論將葉片沿徑向分為有限個微段，稱之為“葉素”，通過計算葉素上受到的升力和阻力，然后將每個葉素的受力進行積分，進而得到葉片所受的氣動荷載。通過葉素理論求得的軸向力和扭矩分別為

式中，Cn=Clcosφ+Cdsinφ，Ct=Clsinφ-Cdcosφ，Cl、Cd分別為升力系數和阻力系數，B為葉片數，

考慮葉尖與輪轂處的修正因子，求得軸向和切向誘導因子a和，最后對dT和dM求積分，得到葉片上作用的推力和扭矩分別為

2.3 波浪載荷

波浪荷載采用三維勢流理論計算[12]，基于勢流理論，波浪荷載由繞射力、輻射力和流體靜力三部分組成，波浪荷載的表達式為

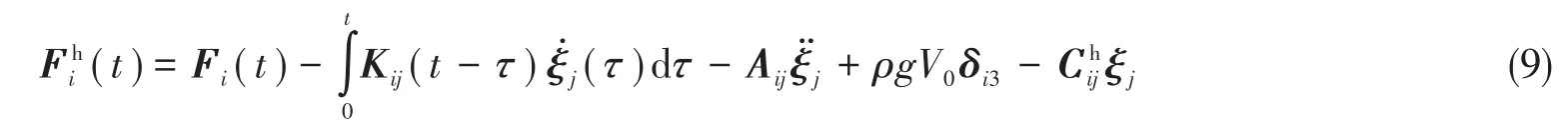
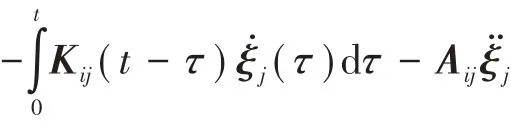
2.4 海流載荷

假設海流為沿水深變化的剪切流。海流對平臺的作用力可由下式計算[10]：

式中，CD為拖曳力系數，ρw為海水密度，A為結構在與流速垂直平面上的投影面積，V為海流速度。

2.5 系泊載荷

本文系泊系統采用FAST軟件FEAM 模塊建模，該模塊基于細長桿理論計算浮式平臺導纜孔處的系泊纜張力。細長桿理論假定桿件為具有任意幾何形狀的彈性體，受到多種環境荷載的作用，應用有限元的方法求解非線性方程，進而得到系泊纜的動力響應。

3 水動力特性分析

3.1 頻域水動力計算

頻域水動力計算的目的是為了分析新型半潛式風機在不同周期的波浪作用下的運動響應規律，得到反映其水動力性能的各項水動力參數，在設計時使基礎的固有頻率避開波浪能量集中的周期范圍，防止共振發生。使用SESAM 的HydroD模塊進行頻域水動力計算，建立的水動力模型如圖2所示。考慮結構的對稱性，浪向角計算范圍選取0～180°，間隔步長15°；波浪周期計算范圍為2～60 s，間隔步長1 s；在頻域計算中不設置系泊錨鏈的約束，根據文獻[13]的建議取臨界阻尼的10%作為結構的粘性阻尼，對計算結果進行修正。

圖2 水動力模型Fig.2 Hydrodynamic model

幅值響應算子（RAOs）是表征入射波浪激勵與浮式基礎運動響應關系的函數，圖3 所示為浮式平臺在縱蕩、垂蕩、縱搖三個自由度上RAO 曲線。從圖中可以看出：由于不考慮錨鏈的約束，浮式基礎的縱蕩RAO 曲線的整體趨勢是隨著入射波周期的增大而增大。在浪向角為0°和180°時，因與縱蕩方向共線，故縱蕩RAO 最大，波浪沿90°入射時，縱蕩RAO 接近0，垂直方向入射的波浪對縱蕩響應幾乎沒有貢獻。垂蕩RAO 曲線在19 s 達到峰值，為1.43 m，波浪周期在19 s 之前垂蕩RAO 較小，在周期大于19 s的范圍，隨波浪周期的不斷增大，垂蕩RAO 逐漸接近1 m。浮式平臺在不同波浪入射角下的垂蕩RAO基本一致。縱搖方向上，隨波浪周期的增大，運動縱搖RAO呈現整體先增大后減小的趨勢，在28 s達到峰值，波浪入射方向為0°和180°時，對縱搖RAO影響最大，最大幅值為0.025 rad（≈1.43°）。由此看出，三個自由度的固有周期較好地避開了波能集中的周期范圍，能夠避免共振的發生，結構設計較為合理。

圖3 浮式平臺運動RAOsFig.3 Motion response amplitude operators of floating foundation

3.2 自由衰減分析

為了準確得到新型半潛式浮式風機的固有周期，在無風、無浪的靜水環境中進行了自由衰減分析，圖4為各自由度的自由衰減時程曲線和功率譜，由功率譜圖得到浮式風機6個自由度的固有周期，如表2所示。

圖4 新型半潛式浮式風機自由衰減時程曲線與功率譜圖Fig.4 Free decay curves and power spectral density of new semi-submersible FOWT

表2 新型半潛式浮式風機固有周期Tab.2 Natural periods of new semi-submersible FOWT

4 不同流速下的耦合動力響應分析

本章重點研究流速對新型半潛式風機的耦合動力特性的影響。根據IEC 61400-3[14]提供的Kaimal風速譜生成平均風速為11.4 m/s的湍流風；基于Jonswap譜生成不規則波浪，有義波高Hs=3.0 m，譜峰周期Tp=10.0 s，峰形參數γ=1，使用全QTF法考慮了二階差頻波浪力的作用；定義海流為流速沿水深線性變化的剪切流，設置了四種不同的流速條件，其中底層流速為0.2 m/s，表面流速分別為0.5 m/s、1 m/s、1.5 m/s和2 m/s。風、浪、流的作用方向均沿X正方向，模擬時長為3小時。在統計分析時，去掉前200 s 的數據以消除風機啟動造成的影響。由于數據量較大，為更好地展示規律性，選取其中1000～2000 s的數據進行展示。

圖5 和圖6 分別為不同流速條件下浮式風機各動力響應參數的時程曲線和統計規律，可以看出：流速從0.5 m/s 到2 m/s，縱蕩響應的最大值、最小值和平均值隨著流速的增大而增大，流速為2 m/s 時的縱蕩最大值為6.70 m，與流速0.5 m/s、1.0 m/s和1.5 m/s時相比分別增加了53.7%、41.4%和20.5%，縱蕩的標準差有減小的趨勢，因此流速增大使得浮式風機的水平運動處在一個更大的位移區間，響應的變化幅度呈現減小的趨勢；垂蕩響應的各統計值比較接近，流速的增大對浮式風機垂蕩運動的影響較小；浮式風機縱搖響應的平均值隨流速的增加呈略微減小的趨勢，因此流速增大、縱蕩的增加引起錨鏈拉伸程度增大，對縱搖響應有一定抑制作用，但作用相對較小；隨著流速的增大，艏搖響應的最大值、最小值的絕對值減小，艏搖運動在一個運動幅度更小的區間內進行，且艏搖標準差減小，說明流速增大削弱了不對稱荷載的影響，對艏搖運動有一定的抑制效果；在同樣風浪條件下，流速改變對發電功率基本沒有影響；隨著流速增大，流荷載引起浮式基礎的水平推力增大，其中受力最大的1 號錨鏈拉力顯著增大，流速2 m/s 下1 號錨鏈拉力為2.17×106N，與流速0.5 m/s、1.0 m/s 和1.5 m/s 時相比分別增加35.6%、29.2%和15.4%。

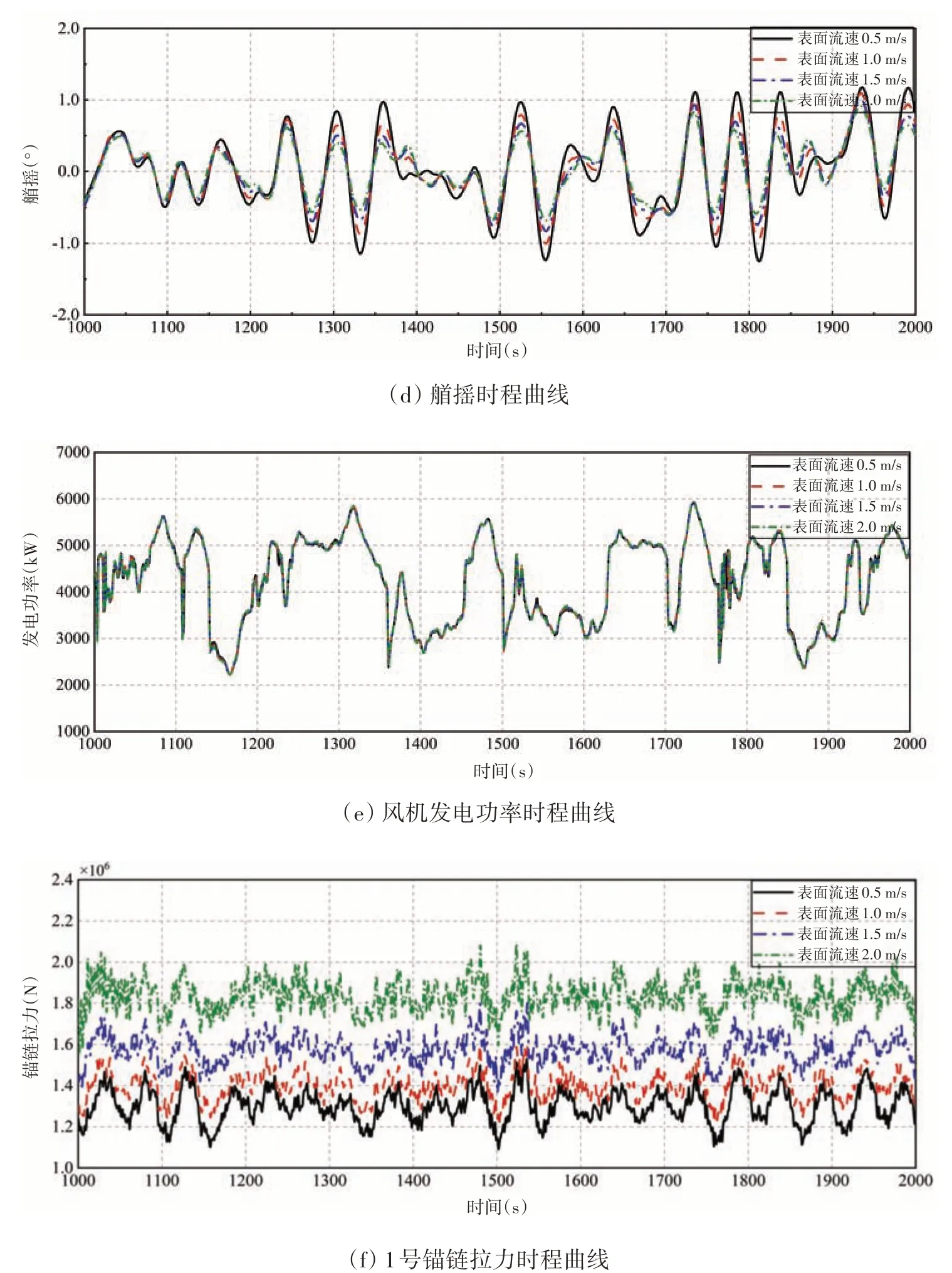
圖5 不同流速下浮式風機各動力響應參數時程曲線Fig.5 Time history curves of dynamic response parameters of FOWT under different current velocities

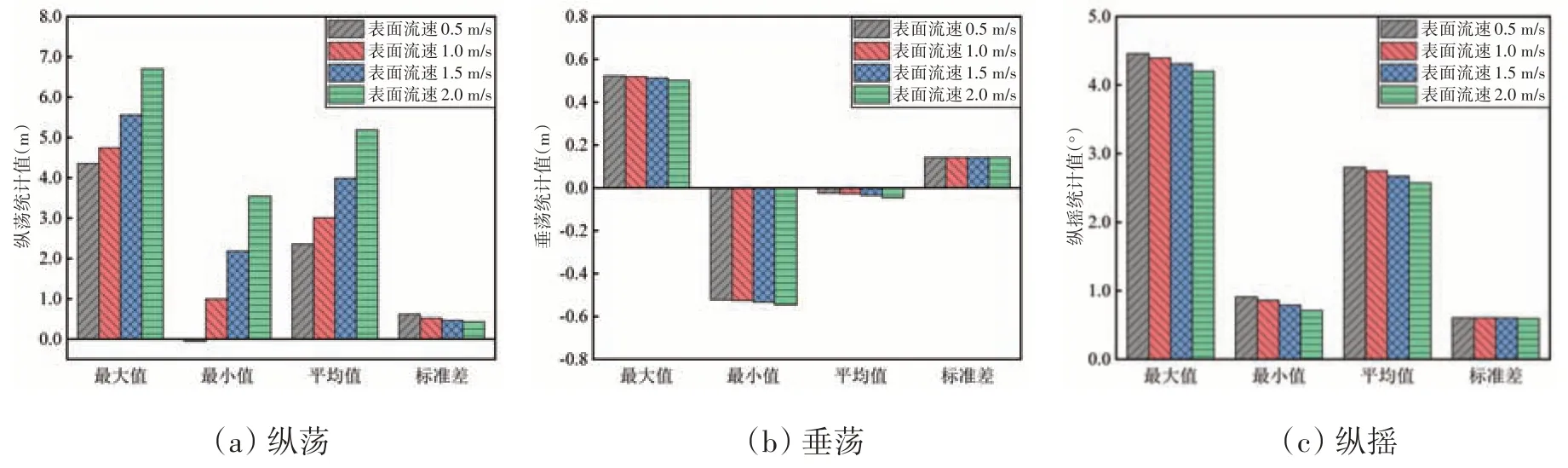
圖6 不同流速下浮式風機各動力響應參數統計規律Fig.6 Statistical characteristics of dynamic response parameters of FOWT under different current velocities

圖7為新型半潛式浮式風機在不同流速下各動力參數響應的功率譜密度。可以看出，縱蕩運動主要由縱蕩共振響應主導，隨著流速的增大，縱蕩共振響應逐漸減小。垂蕩運動主要由波頻響應主導，垂蕩共振響應較小，受流速變化的影響不明顯。對于縱搖運動，響應集中在風頻率、縱蕩共振頻率和縱搖共振頻率處，受流速變化的影響不明顯，波頻響應較小。艏搖功率譜密度曲線中，兩個主頻對應艏搖共振頻率與縱蕩共振頻率，隨著流速增大，共振響應顯著減小。發電功率的功率譜密度曲線中，響應集中在風頻率，主要受風荷載影響。錨鏈拉力譜密度規律與縱蕩類似，受縱蕩共振響應的影響較大。