基于博弈論的一體化防撞梁多目標優化設計*

李書華 吳宗揚 貝璟 余承斌 張代勝

（1.合肥工業大學，智能制造技術研究院，合肥 230051；2.合肥工業大學，汽車與交通工程學院，合肥 230009；3.合肥長安汽車有限公司，合肥 230031）

主題詞：一體化防撞梁 博弈論 碰撞安全性能 納什均衡 多目標優化

1 前言

在低速正面碰撞過程中，最先承擔緩沖吸能作用，進而保證乘員安全的被動安全部件是防撞梁，國內外許多學者對其展開了廣泛的研究[1]。Wang[2]等采用非支配排序遺傳算法-Ⅱ（Non-dominated Sorting Genetic Algorithms-Ⅱ，NSGA-Ⅱ）和電子搜索算法（Electronic Search Algorithms，ESA）對負泊松比保險杠系統的結構參數進行尋優。賀良國等[3]運用NSGA-Ⅱ對多胞結構的車身前端結構參數進行尋優。徐峰祥[4]采用NSGA-Ⅱ對拼焊板結構進行了多目標優化設計。上述文獻使用的傳統優化算法在進行耐撞性多目標優化模型求解時，無法穩定地輸出最優解，且未考慮不同結構參數對優化目標的不同影響，從而降低了最終方案的優化效果。

博弈論作為一種研究具有斗爭或競爭性質現象的數學理論和方法，已被廣泛應用于各個領域。Staňková等[5]使用博弈論方法優化了癌癥的治療。胡永進等[6]構建了多階段網絡欺騙博弈模型，為網絡安全主動防御研究提供有效指導。防撞梁的耐撞性與輕量化之間的矛盾性可視為一種博弈問題，由于博弈理論中納什均衡解具有“穩健性”和“自我強制性”的特點，使得多目標優化模型能夠穩定而客觀地輸出最優解[7]。

綜上，針對一體化防撞梁的耐撞性和輕量化設計問題，本文提出一種基于博弈論的防撞梁多目標優化方法。首先根據防撞梁的耐撞性和輕量化研究特點以及影響因素分析，將防撞梁的比吸能和質量作為博弈雙方進行博弈，將防撞梁的結構參數作為博弈方的策略集，然后通過引入博弈距離和博弈力矩進行策略歸屬構建，最后通過對博弈方效用函數的對比分析尋找納什均衡點，從而得到優化模型的最優解。

2 方法論

2.1 多目標優化模型與博弈模型的映射關系

從博弈論的角度思考，多目標優化設計問題與博弈決策問題有如下關聯[8]：

a.將多目標優化模型視為博弈模型。

b.設計變量X及其取值范圍對應博弈決策問題的策略集C及其可行空間，可通過一定方法將設計變量X拆分為策略集C1,C2,…,Cq。

c.將優化目標視為博弈決策問題的博弈方，將優化算法視為納什均衡分析。

d.多目標優化設計問題的目標函數的響應值等同于博弈決策問題中博弈方所獲得的效用，且兩者的約束也可視為一致。

故可用博弈決策問題的思維方式來描述多目標優化設計問題：

式中，G為多目標優化模型空間集合；V1,V2,…,Vq為q個博弈方；C1={xi,…,xj},…,Cq={xk,…,xl}為q個博弈方的策略集，并滿足C1∪C2∪…∪Cq=X且Ca∩Cb=0；a,b=1,2,…,q且a≠b。

2.2 優化流程

對防撞梁進行多目標優化設計的目的在于獲得耐撞性和輕量化函數的最優解。優化過程主要分為3 個階段，即策略歸屬構建、效用函數構建和納什均衡分析，優化流程如圖1所示。

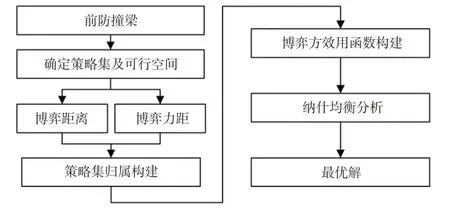
圖1 防撞梁的博弈優化設計流程

2.2.1 策略歸屬構建與博弈效用函數構建

博弈方的策略集歸屬構建是多目標優化設計問題轉為博弈決策問題的關鍵。為此，引入博弈距離和博弈力矩的概念[9-10]：

a.博弈距離。博弈距離定義為項目i到博弈方v的距離與所有項目到與其對應的各博弈方距離之和的比，其中，項目i到博弈方v的距離表示為uv,i的倒數：

式中，?i∈[1,…,n]；?v∈[1,…,q]；uv,i為項目對i博弈方v的效用；n為博弈方的數量；dv,i為項目i到博弈方v相對于其他博弈方的博弈距離。

b.博弈力矩：

式中，φv,i為項目i到博弈方v相對于其他博弈方的博弈力矩。

策略集歸屬構建步驟如下：

a.通過粒子群算法對各目標函數進行單目標優化，得到初始效用和初始策略集。

b.按照式（2）和式（3）計算博弈距離和博弈力矩，對于某一個博弈方vw，將各項目到博弈方vw的博弈距離按照升序排列，表示其優先級順序從高到低，并按照博弈距離排列順序計算相對應的累加博弈力矩。

同時，為了簡化優化過程，從而提高優化效率，需要將模型仿真替換為數值優化，因此，博弈效用函數的構建是必不可少的。

2.2.2 納什均衡分析

設X={x1,x2,…,xq}=C={C1,C2,…,Cq}為博弈方的策略集，V1(c),V2(c),…,Vq(c)為博弈所獲得的效用，博弈流程如下：

a.基于博弈距離和博弈力矩，得到隸屬于各博弈方的策略集{C1,C2,…,Cq}。

3 有限元模型建立與可行性檢驗

3.1 正面碰撞有限元模型建立

汽車前防撞梁能在低速碰撞中起到吸能和緩沖的作用[11]。本文采用臺車正面碰撞有限元模型對防撞梁的低速正面碰撞性能進行仿真，如圖2 所示，臺車模型質量為1 530 kg，臺車以1.111 m/s的初始速度撞向剛性墻，整個碰撞過程時間設定為0.06 s。該一體化精密鑄造防撞梁的材料選用ZL205A 鋁合金，其密度為2.82×103kg/m3，彈性模量為7.3×104MPa，泊松比為0.32。考慮應變速率對材料應力-應變曲線的影響，材料類型選擇MAT24。

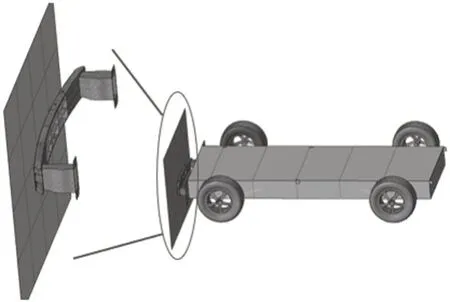
圖2 臺車正碰有限元模型

3.2 有限元模型可行性檢驗

能量守恒是判斷正面碰撞有限元模型是否可靠的重要標準。簡化積分方法往往會導致沙漏模式，從而損失部分能量，影響系統的仿真精度[12]。一般要求質量增加不超過5%，總能量增加不超過10%，產生的沙漏能不超過總能量的5%，且不為負值。針對防撞梁低速正碰仿真模型，碰撞過程中的能量變化如圖3所示，從圖3中可以看出，總能量處于平穩狀態，沙漏能幾乎為零，能量始終守恒，故碰撞模型合理，可用于后續優化設計。

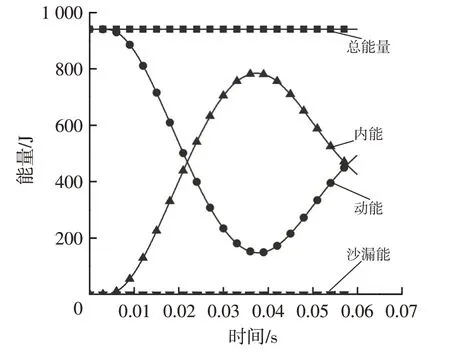
圖3 能量變化曲線

4 防撞梁博弈優化

4.1 初始設計分析

防撞梁的耐撞性評價指標可以用比吸能、峰值碰撞力和吸能量來衡量。此外，為了保證乘員具有充足的生存空間，防撞梁在碰撞過程中的最大縱向位移也不應超過許可值[13]。一體化精密鑄造防撞梁的初始效用如表1所示，由于最大縱向位移和峰值碰撞力的矛盾性，從表1 中可以看出，最大縱向位移的安全設計余量較大，而峰值碰撞力過大，存在一定安全隱患。為了進一步增強防撞梁的碰撞安全性能，需對其進行輕量化和耐撞性優化設計。

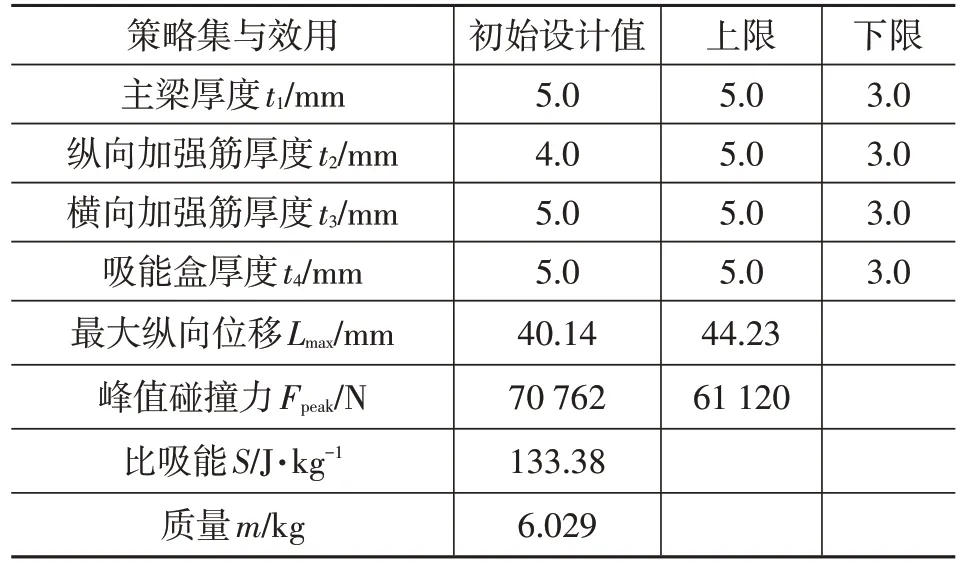
表1 設計變量及響應的初始效用

4.2 策略分析

如圖4所示，本文選取防撞梁的主梁、縱向加強筋、橫向加強筋和吸能盒的厚度（t1～t4）為策略集，并以峰值碰撞力Fpeak和最大縱向位移Lmax為約束條件，以防撞梁的比吸能S和質量m為博弈方，比吸能和質量的響應值為博弈方所獲得的效用。

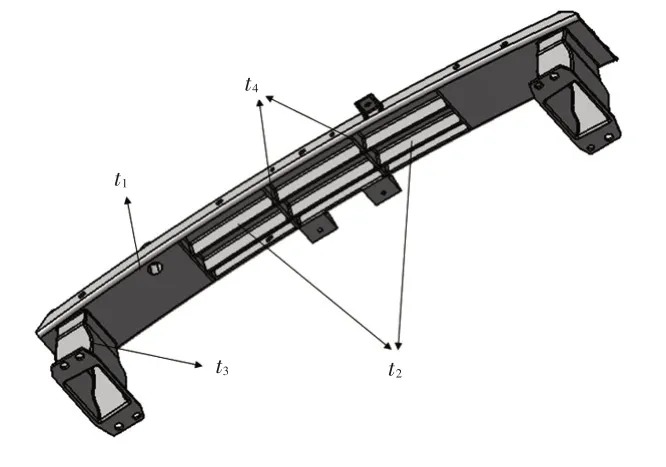
圖4 防撞梁的厚度變量

按照策略集劃分步驟，首先對防撞梁的比吸能和質量分別采用粒子群單目標優化算法（種群大小為100，迭代次數為30，慣性權重因子為0.9，學習因子c1和c2取0.9），得到初始效用和初始策略集。根據式（2）和式（3）分別計算各博弈方的博弈距離和博弈力矩，如表2 所示。

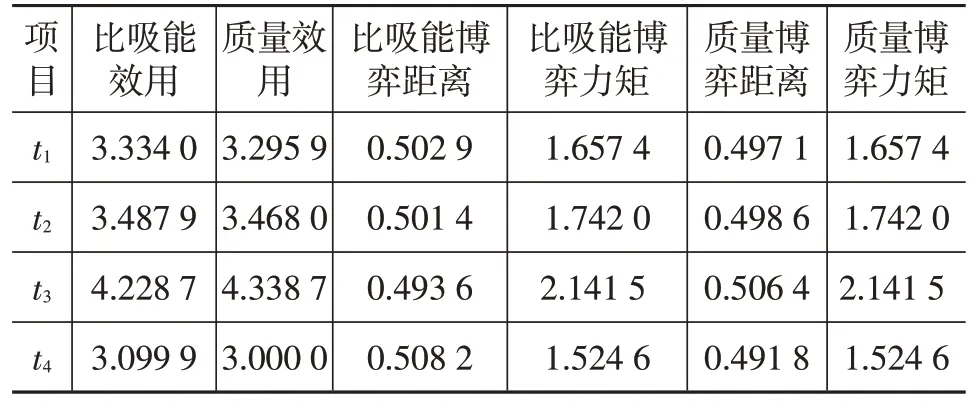
表2 各項目的效用、博弈距離和博弈力矩

根據表2中比吸能的博弈距離進行升序排列，并根據博弈力矩φs,ti計算相對應的累加博弈力矩ai，如表3所示。計算可得平衡值uv=3.532 8，通過比較平衡值uv和各項累加博弈力矩來確定屬于博弈方比吸能的策略集，即C1=(t2,t3)，其他的項目為博弈方質量的策略集，即C2=(t1,t4)。

表3 各項目的累加博弈力矩

4.3 博弈效用函數構建

博弈效用函數采用響應面法構建，它能通過試驗設計所得到的樣本數據來探測輸入變量與輸出響應之間的敏感度，最終將其擬合成函數關系，從而把結構優化問題轉化為數值優化問題，大幅提高優化效率。

試驗設計方法的選擇對構建高精度的效用函數很重要。本文采用最優拉丁超立方試驗設計方法構建響應面模型，它能將試驗設計點均勻地分散在設計空間中，具有很好的空間填充性和均衡性[14]。采用30個采樣點來構建防撞梁峰值碰撞力、最大縱向位移、比吸能和質量的二次響應面近似模型，并且通過不斷增加試驗設計點來更新近似模型，直到近似模型的精度滿足要求。本文主要采用確定系數R2對響應值進行精度評價，Lmax、Fpeak、S、m的確定系數分別為0.999、0.927、0.999、0.999，均滿足要求，說明所構建的效用函數是可靠的。

4.4 結果與討論

4.4.1 納什均衡分析

隨機確定初始策略集，基于納什均衡分析，博弈方的比吸能和質量的迭代過程如圖5所示，從圖5中可以看出，在第10次迭代時，質量最小，比吸能達到最大，滿足收斂準則。經過協調權衡，峰值碰撞力與最大縱向位移均在安全范圍內。

圖5 博弈方迭代過程

4.4.2 各類優化算法對比分析

采用粒子群多目標優化算法、多島遺傳算法以及非支配解排序遺傳算法分別對防撞梁數學模型進行求解，其中，各類優化算法相關參數設置如表4 所示，優化結果如表5所示。從表5中可以看出：傳統優化算法相比于博弈優化設計，比吸能均偏小，而質量均偏大；且博弈法是一種帶有競爭性質的純策略型方法，博弈雙方存在“互利”解，只需較少的迭代次數便能找到納什均衡點，求解穩定且速度快；對比初始設計，經博弈設計的防撞梁的質量減輕了26.47%。初始設計與博弈設計的防撞梁比吸能變化過程如圖6所示，由圖6可知，比吸能增長了22.18%，博弈設計提高了防撞梁的碰撞安全性能。

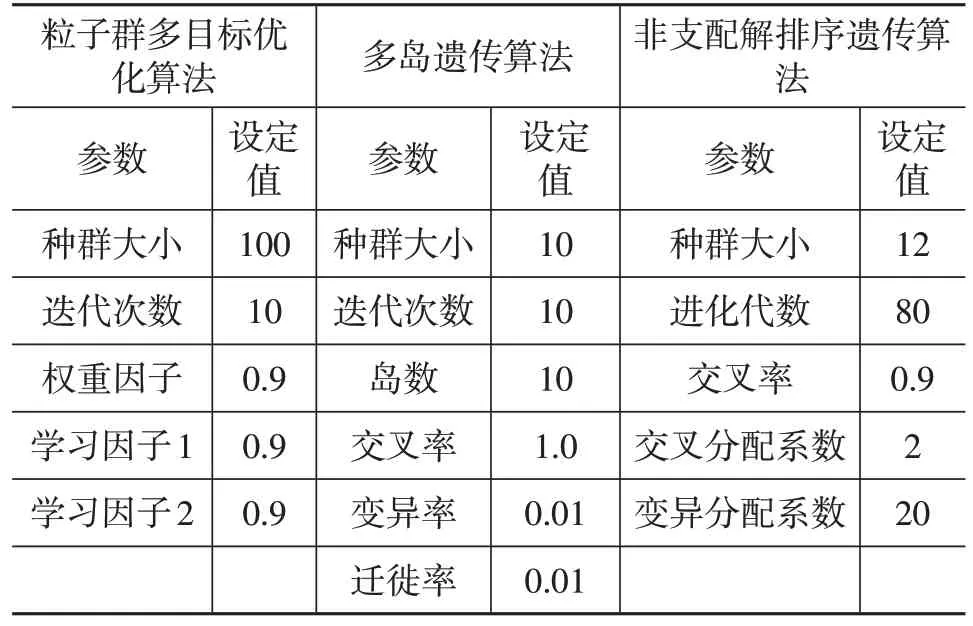
表4 優化算法參數設置

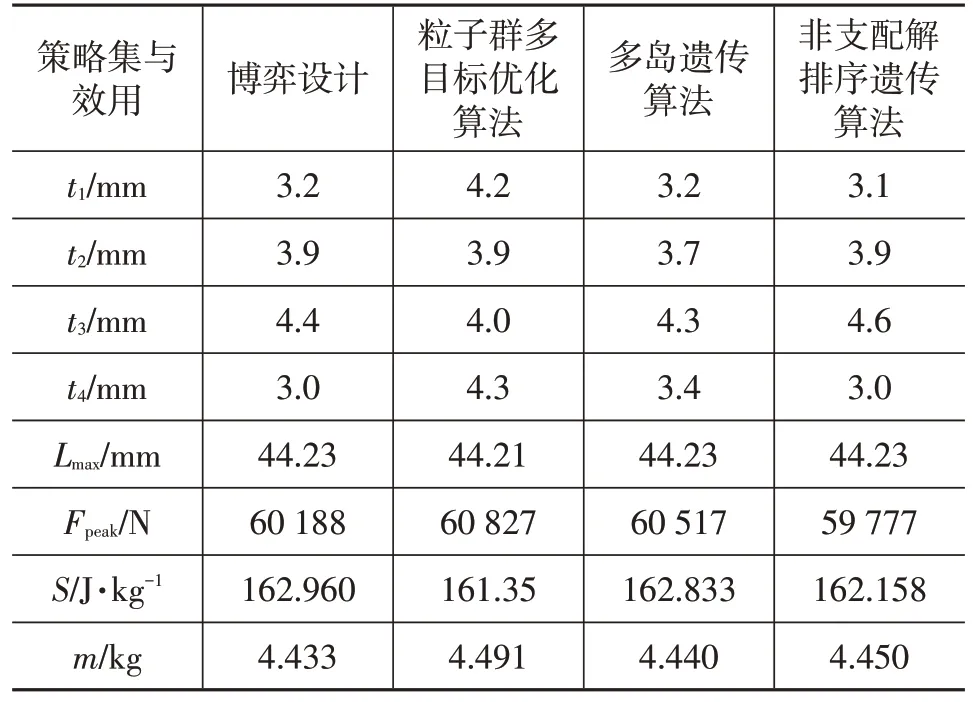
表5 優化結果對比

圖6 初始設計與博弈設計的比吸能對比

5 結束語

本文采用“材料-結構-性能”一體化集成設計方法，能夠對防撞梁進行有效優化，在保證良好的整體性能的情況下，實現防撞梁的輕量化設計。針對一體化防撞梁的耐撞性和輕量化設計特點，以比吸能和質量為博弈雙方，提出了一種基于博弈論的防撞梁多目標優化方法。同時，將防撞梁多目標優化模型與非合作博弈模型進行映射，結合博弈模型的特點，基于博弈距離和博弈力矩對結構參數進行策略歸屬構建。

通過對效用函數的納什均衡分析，經過10 次迭代達到收斂準則，避免了最大縱向位移安全系數設計過大的缺陷。結果表明：博弈設計的防撞梁的峰值碰撞力與最大縱向位移均在許可范圍內，且相比于初始設計，防撞梁質量減輕了26.47%，比吸能增加了22.18%，相比于傳統多目標優化算法，博弈設計具有更好的穩定性和優化效果，證明了其實用性與有效性。