透明液體質量分數與折射率關系的居家實驗
胡凱琦,王慧琴,賴盛英,樊偉征
(上海工程技術大學 a.數理與統計學院;b.電子信息工程學院,上海 201620)
液體質量分數是描述溶液的重要物理量. 測量液體質量分數的方法較多,常見的物理測量法有折射率法[1-4]、旋光率法[5]、光譜分析法[6]等,其中折射率法應用最為廣泛,該方法通過研究液體質量分數與折射率的關系定標出待測液體的質量分數. 一般地,透明液體質量分數與折射率在一定范圍內呈線性關系[7],因此測出待測液體的折射率,即可求出其質量分數值. 本實驗是在居家條件下,通過簡單的實驗材料,利用2個面(成一定夾角)的折射,較為精確地測得不同質量分數的NaCl溶液折射率,通過擬合得到液體質量分數與折射率的關系式,通過比較該關系式與經驗公式吻合. 與傳統實驗相比,本文方案具有實驗材料容易獲得、不需要精密儀器設備、操作簡單、物理圖像清晰、實驗結果精度較高等優點,因此該實驗既可作為演示實驗,也可作為探索性實驗,實驗裝置還可改裝成液體質量分數測定儀.
1 實驗原理
1.1 兩面折射法測液體折射率的原理
當水平光線斜入射至盛有透明液體的多邊形玻璃容器時,會發生偏折現象. 設待測溶液的折射率為nx,容器玻璃的折射率為nG,空氣折射率為nA=1,光線的入射角為φ1,光入射到容器某面上的折射情況如圖1所示.由折射定律可知:nAsinφ1=nGsinθ1=nxsinθ2,可見,光線經平板玻璃上下界面折射后會發生平移,但不會改變在液體中的折射角,即對折射方向而言等同于空氣與液體界面上的折射.本實驗所用玻璃厚度為1 mm,測量所需數據只與入射角和折射角有關,因此玻璃對測量結果無影響,故后面將玻璃內部的折射簡化.
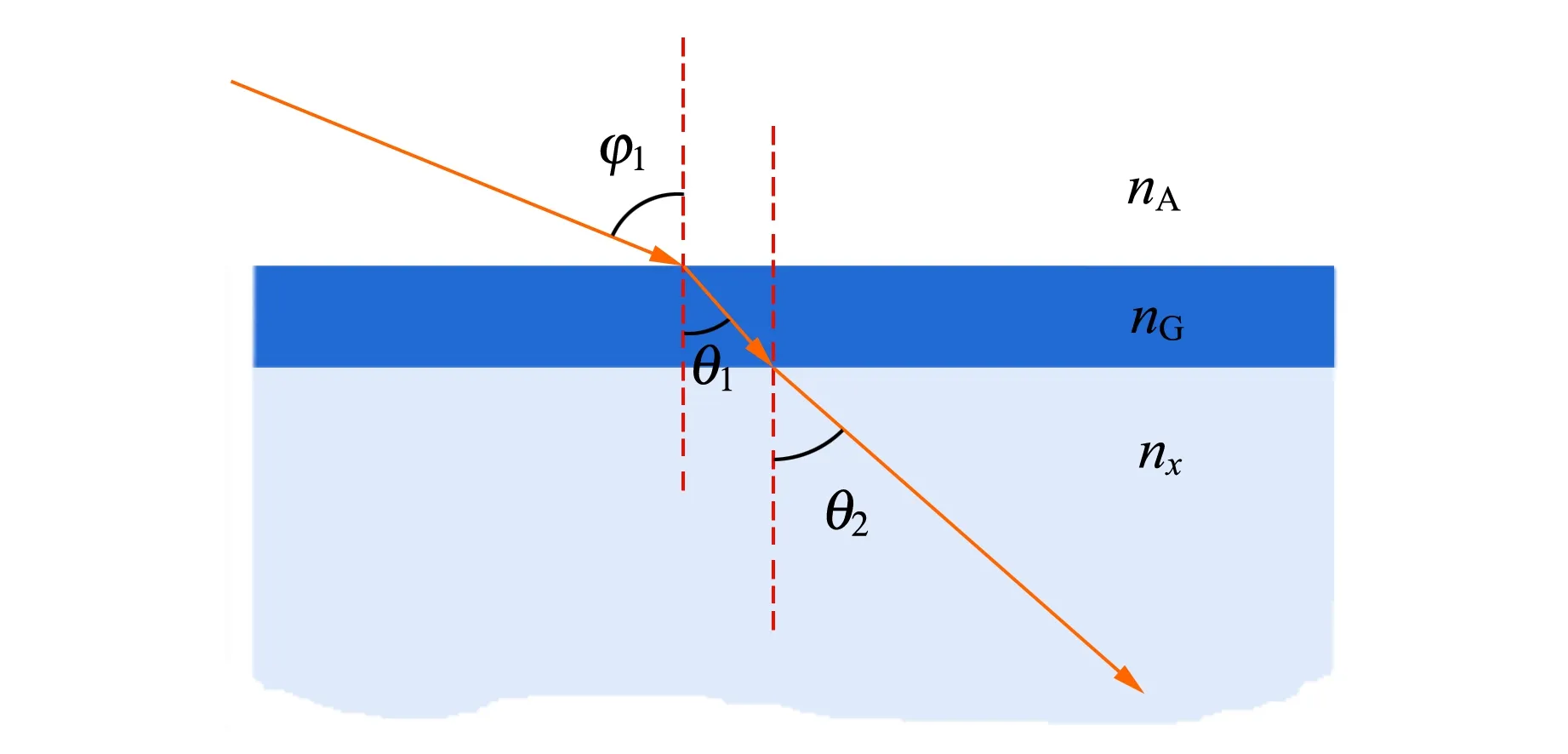
圖1 入射面的折射
若光經容器的2個面后出射,且入射面與出射面的夾角為α,出射角為φ2.由于φ1,α和nx的取值不同,可能出現θ2+θ3=α和θ2-θ3=α的2種情況,如圖2所示.對應的液體折射率表達式分別為
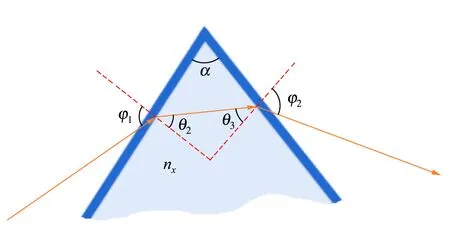
(a)θ2+θ3=α
(sinφ1≤nxsinα)
(1)
(sinφ1>nxsinα)
(2)
由式(1)~(2)可知,要測出液體折射率nx,只需測出φ1,φ2和α即可,計算時要根據φ1,α和nx的實際值選擇合適的表達式.
對于常見透明液體,其折射率范圍為1.33~1.45,當α=90°時,1.33 全發射是由光密到光疏介質時光全部被反射回光密介質的現象.在本實驗中,光在入射面玻璃到液體和出射面玻璃到空氣都有可能發生全發射,因此需要選擇合適的入射角才能避免全反射的發生,保證所有質量分數液體都可測量. 居家條件下沒有專業的測角儀,實驗中利用2塊平面鏡通過幾何關系將角度測量轉換為線度測量,一塊平面鏡與出射面共面,另一塊平面鏡與之平行.以三角形容器為例的實驗裝置示意圖見圖3,光線經器皿的2個面折射后出射到右側標尺上,留下光點1;在光點1處插入反射鏡1,該光點經反射后到左側反射鏡2上,再反射回到標尺上,并留下光點2,記錄下兩光點位置,求出兩光點的間距,測出兩鏡面間的距離d,則 圖3 液體折射率測量裝置示意圖 (3) 將式(3)代入式(1),可得 (4) 可見,該方案除了利用幾何關系把角度的測量轉變成距離的測量,還利用了光杠桿原理,將由液體質量分數變化引起的出射角的微小變化量轉變成容易觀察的距離變化,提高了測量精度. 實驗前準備: 1)將普通載玻片粘合制作成方形和三角形的空心容器. 2)用食鹽與水混合,使用精度為0.01 g的電子秤,分別配制13種質量分數的NaCl溶液. 3)用半導體激光筆、玻璃容器、平面鏡、標尺、量角器等器材組建液體質量分數測量裝置,如圖4所示. (a)方形容器測量裝置 (b)三角形容器測量裝置 實驗步驟: 1)調整激光筆使出射的激光水平,容器、鏡面均豎直,以70°入射至容器的入射面,觀察出射光的位置,將光屏平行于出射面放置,使出射光斑照在光屏上,固定光屏; 2)在光屏前光斑處豎直放置平面鏡1(本實驗采用自粘鏡片直接貼在屏上),觀察經平面鏡反射后光線的方位; 3)在反射光線的方位上豎直放置平面鏡2,保持鏡面2與出射面共面,經鏡2反射,在光屏面內能接收到第2次反射回來的光點(若距離大,則需要2個光屏,且要使兩光屏共面. 本實驗采用一條形板貼上白紙作為光屏,板上貼有米尺和鏡片1); 4)打開激光筆,分別記下第1個光斑位置x1和第2個光斑位置x2,二者相減得到Δx(多次測量取平均值). 5)測出兩鏡面間距d,求出被測溶液的折射率. 6)保持入射角不變,更換不同質量分數的溶液(裝置底部接有軟管和節流閥,直接打開節流閥即可排空液體)進行測量,得到若干組數據,通過擬合即可得到該溶液質量分數與折射率的關系. 7)改變入射角,分別在入射角為75°和80°的情況下,重復上述步驟. 在入射角φ1為70°,75°,80°情況下,分別采用不同容器對質量分數w為2%~26%的NaCl溶液進行了測量,測量時方形容器裝置的兩鏡面間距為3.1 cm,三角形容器裝置鏡面間距為45.6 cm,每種液體均測量5次取平均值,代入式(4)即可得到待測液體的折射率. 方形容器測得的NaCl溶液的實驗數據如表1所示(α=90°,d=3.1 cm),對表1數據通過最小二乘法擬合得到液體質量分數與折射率呈線性關系,且3條擬合直線基本重合,如圖5所示. 其中,入射角φ1=70°,75°,80°的情況下折射率與溶液質量分數的擬合關系式分別為:n=1.334+0.001 82w,n=1.333+0.001 83w,n=1.333+0.001 83w. 不同入射角情況下的擬合關系式與經驗公式nNaCl=1.333+0.001 85w吻合[7]. 表1 方形容器測得NaCl溶液的實驗數據 圖5 方形容器內NaCl溶液質量分數與折射率關系圖 三角形容器內NaCl溶液實驗數據及擬合結果如表2和圖6所示(α=64°,d=45.6 cm),結果同樣表明折射率與質量分數呈線性關系,3個不同入射角下擬合的關系式分別為:n=1.332+0.001 92w,n=1.327+0.002 08w和n=1.332+0.001 91w. 測量結果與經驗公式[7]吻合較好. 圖6 三角形容器內NaCl溶液質量分數與折射率關系圖 表2 三角形容器測得NaCl溶液的實驗數據 比較方形與三角形容器的測量結果可知,方形容器測量條件下的光線偏移量Δx隨質量分數變化更快. 這是由于在相同條件下,方形容器的出射角大于三角形容器的出射角,當d相同時,較大的出射角可獲得更大的光點間距Δx,因此方形容器比三角形容器更易觀察,相對靈敏,實驗結果更好,測量結果與經驗公式吻合更好. 但對于方形容器而言,當入射角為70°時,質量分數較高的液體更易接近臨界反射或全反射,從而不便觀測. 本實驗從基本的折射定律入手,利用容器2個面的折射,再利用光杠桿原理放大質量分數變化引起的折射角度變化,且將角度的測量轉變成距離的測量,較精確地測出了NaCl溶液在不同質量分數下的折射率,實驗結果驗證了溶液質量分數與折射率的線性關系,且擬合公式與經驗公式吻合,說明該方法具有可行性. 實驗不需要精密的儀器和設備,只需一些簡單的實驗材料,操作簡單、物理圖像清晰. 該實驗既可作為演示實驗,也可作為探索性實驗,其實驗裝置還可改裝成液體質量分數測定儀. 本文以方形和三角形容器為例展開研究,但本實驗方案所推導的公式是普適的,對任意多邊形任意角度的容器均適用.1.2 全反射限制及入射角的選擇

1.3 出射角的測量方法

2 實驗操作

3 液體質量分數與折射率的關系
3.1 方形容器的測量結果
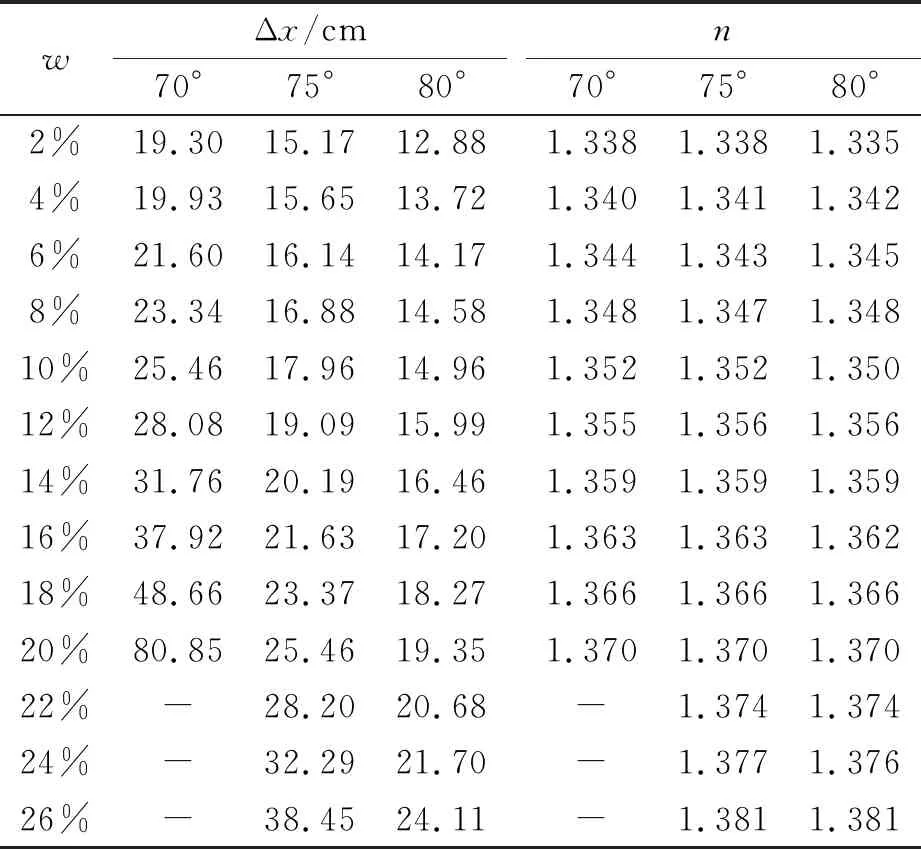

3.2 三角形容器的測量結果

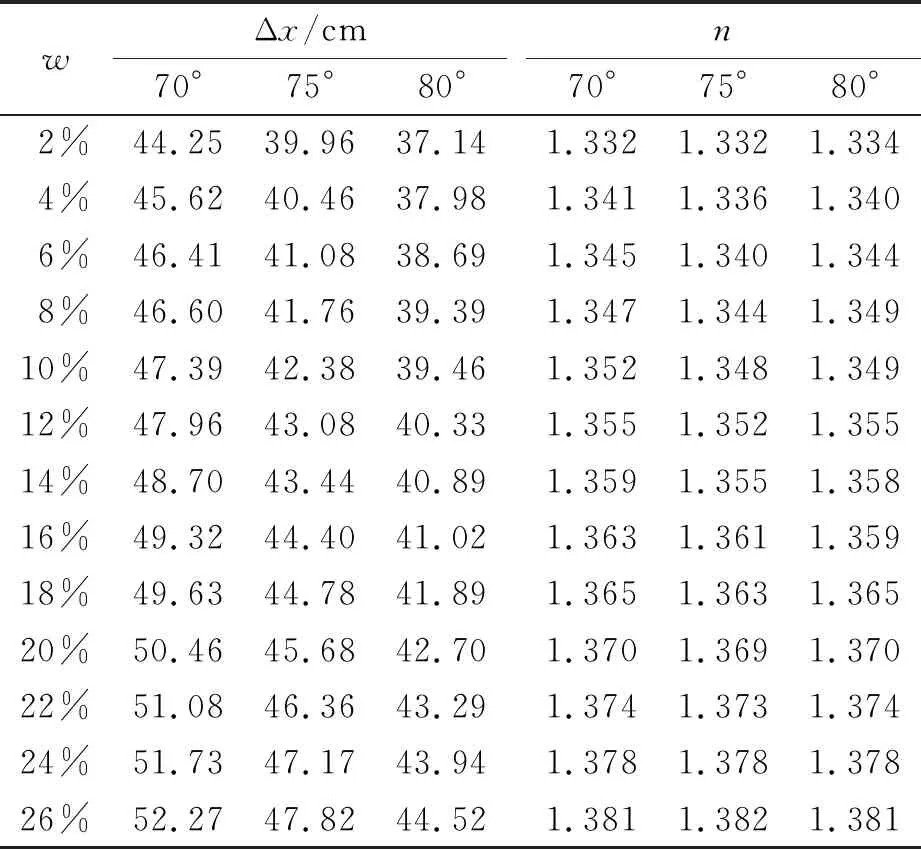
4 結束語

