基于曲線擬合的自動壓濾機脫水過程優化

劉惠中， 鄧浩宗

(1.江西理工大學機電工程學院， 贛州 341000; 2. 江西省礦冶機電工程技術研究中心， 贛州 341000)

隨著易選礦物資源的逐漸枯竭，低品位礦石的研磨粒度變細導致礦物的脫水變得越來越困難[1]，精礦的水分含量將直接影響后續的冶煉工序。壓濾脫水過程的核心設備為壓濾機[2]。壓濾機分為板框壓濾機、快開式壓濾機及自動壓濾機。相比于板框壓濾機和快開式壓濾機，自動壓濾機增加了橡膠隔膜壓榨、空氣干燥、自動卸餅及濾布清洗過程等脫水過程，所以，自動壓濾機的生產及脫水效率最高，脫水過程也最為復雜。其中，每個脫水過程都由時間來控制，目前，中國對壓濾機脫水過程時間的確定主要以操作工人的經驗為主，這容易導致壓濾機工作效率低。因此，優化壓濾機的相關脫水工作過程從而提高其過濾效率和生產效率具有重要意義。

中外學者對于壓濾機工作流程改進和壓濾參數優化做了相關研究。朱桂華等[3]通過建立壓濾機單濾室網格仿真模型，分析不同壓力下濾液總量隨時間變化的規律確定最佳過濾壓力;Zhang等[4]的通過大量生產數據，利用引力搜索算法-遺傳算法(gravitational search algorithm-genetic algorithm，GSA-GA)算法建立壓濾脫水的兩步優化模型，研究了不同參數濾餅水分和壓濾機工作時間的關系；Raman等[5]通過多次的壓濾機實驗數據建立起人工神經網絡模型(artificial neural networks，ANNs)，以濾餅水分為響應變量，研究了濾餅水分與時間等變量的變化規律。

上述研究可以看出，目前有關壓濾機的工作流程優化研究大多是通過建立復雜網格仿真模型進行優化分析或者是利用大量實驗數據進行相關分析。利用仿真軟件進行優化分析能夠得到較為精確的結果，但是針對不同的研究對象需要建立不同的復雜網格仿真模型，同時對于不同種類礦漿以及不同型號壓濾機需要設置不同的仿真參數，不具有繼承性，導致研究過程比較繁瑣；現場實驗法能夠獲得真實可靠的實驗數據，但是大量的實驗需要消耗大量的資金成本和時間成本，并且難以保證每次的實驗條件相同。

根據統計學理論以及壓濾機濾液總量與壓濾時間的變化關系，基于曲線擬合方法，現利用少量的實驗數據分別對壓濾機的壓濾階段、壓榨階段和空氣干燥階段分別進行流程優化分析，得到各階段的最優工作時間，最終實現壓濾機的整體工作流程優化。該方法既能夠避免建立復雜網格仿真模型，也不需要大量的實驗數據。同時得到壓濾機3個工作階段的濾餅水分和工作時間的回歸方程，可以根據需要的濾餅水分調整各階段壓濾時間。最后將分析結果與實際生產數據對比，驗證分析結果的可靠性。

1 自動壓濾機優化分析

自動壓濾機的工作流程包括：濾板合攏、給礦壓濾、機械壓榨、空氣干燥、濾板拉開、卸料、濾布清洗等。濾板合攏、濾板拉開、卸料和濾布清洗的工作時間通常是固定的，而給礦壓濾、機械壓榨和空氣干燥階段的工作時間是根據濾餅實際情況進行調整的。因此，將對上述3個階段的工作時間進行優化分析。自動壓濾機的工作周期如圖1所示，ti為當前工作階段所用時間量，Ti(i=0，1，…，6)為壓濾機各工作階段的周期時間，其中T0為濾板合攏階段，T1為給礦壓濾階段，T2為機械壓榨階段，T3為空氣干燥階段，T4為濾板拉開階段，T5為卸料階段，T6為濾布清洗階段。

0～t6為壓濾機的一個完整工作周期，通過縮短T1、T2和T3階段的時間從而實現壓濾機工作流程的優化。

圖1 自動壓濾機工作周期Fig.1 Working cycle of automatic filter press

1.1 給礦壓濾階段

在給礦壓濾階段，礦漿不斷地進入濾室并進行初步壓濾形成濾餅，該階段壓濾過程遵循達西定律：

(1)

式(1)中：Q為濾液流量；t為壓濾時間；V為時間t內的濾液總體積；K為濾層滲透系數；A為過濾面積、ΔP為壓力降；μ為濾液黏度系數；L為濾層厚度。

由式(1)可以看出，濾餅的濾液流量與濾餅面積成正相關、與濾餅厚度成負相關。隨著給礦壓濾時間的增加，處理的礦漿總量也隨之增加，形成的濾餅面積和厚度也會增加。因此，合理地確定給礦壓濾時間來控制濾餅面積和濾餅厚度的比值，從而保證濾液總量最優是壓濾階段的優化目標。

1.2 機械壓榨階段

入料壓濾階段結束以后停止進料，在機械壓榨階段繼續增加壓力對濾餅進行壓榨操作，通過濾板壓縮減小濾室體積，對濾餅進行擠壓從而濾出水分，在該階段，濾餅面積不會增加，濾餅厚度會被不斷壓縮。入料壓濾階段和機械壓榨階段的V-t關系如圖2所示。

V1為給礦壓濾階段的濾液總量；V2為機械壓榨階段的濾液總量；t1為給礦壓濾開始的時間；t1為機械壓榨開始的時間；t2為空氣干燥 階段開始的時間圖2 V-t關系示意圖Fig.2 Diagram of V-t relation

從圖2可以看出，機械壓榨階段的濾液總量存在一個理論極限值，繼續延長壓榨時間無法濾出更多濾液，反而會增加工作周期導致壓濾機效率低下，所以，確定該階段的合理工作時間是機械壓榨階段的優化目標。

1.3 空氣干燥階段

經過機械壓榨后，濾餅孔隙內殘留的水分無法再通過壓榨的方式排出，這時，可以利用壓縮空氣穿透濾餅孔隙從而帶走孔隙內水分以實現降低濾餅含水率。空氣干燥階段大致可分為3個階段[6]：穿透階段、置換階段和蒸發階段，具體效果如圖3所示。

圖3 空氣干燥脫水階段Fig.3 Air drying dehydration stage

從圖3中可以看出，當壓縮空氣完全穿透孔隙后，濾餅孔隙內的水分基本上不再下降，繼續進行空氣干燥只會導致壓縮空氣和工作周期的增加，因此，合理地控制空氣干燥階段的工作時間是空氣干燥階段的優化目標。

綜上所述，自動壓濾機的優化目標是對T1、T2和T3這3個工作周期的時間進行合理優化控制，從而縮短壓濾機的工作周期時間。

min(T1+T2+T3)

(2)

式(2)是本文優化目標模型，根據上述分析，各階段濾液量隨時間變化的規律都有共同特點：濾液量隨著時間的增加而不斷增加，但濾液量增加的速度在不斷降低，直到某一時刻不再增加。因此，采用SPSS 26中非線性回歸的曲線估算對各階段V-t關系進行回歸分析，最終選擇最合適的模型進行擬合并得出擬合公式。

2 曲線擬合分析

對于非線性的數據進行擬合分析時，通常采用非線性模型進行回歸分析，包括廣義線性模型[7]、非參數回歸模型[8]和曲線擬合[9]。

曲線擬合是非線性回歸中的一種分析方法，通過合適的曲線模型對實驗數據進行擬合得出擬合曲線，并通過最小二乘法求出擬合曲線的公式。曲線擬合在多個領域被用于擬合分析，Kozlova等[10]利用非線性曲線對血液中碳氧血紅蛋白含量的濃度進行擬合分析，并得到了精度較高的結果；Tian等[11]利用非線性擬合曲線得到擬合函數，對高效魯棒模型預測控制算法(efficient robust model predictive control， ERMPC )進行了改進，并已應用于實際的快速響應線性一級倒立擺(linear one stage inverted pendulum， LOSIP) 系統；Sun[12]對非線性弱極化區進行曲線擬合計算，得到了腐蝕體系中的極限電流密度和腐蝕電流密度；Parente等[13]通過曲線擬合建立不同模型對不同隕石礦物的反色光譜吸收帶進行擬合分析；顏湘武等[14]基于曲線擬合對虛擬同步發電技術(virtual synchronous generator， VSG)技術中的轉動慣量和阻尼系數進行擬合優化；杜卓等[15]通過非線性最小二乘曲線擬合對離心泵Q-H曲線進行擬合，并消除了駝峰曲線的影響。從上述研究結果可以看出，曲線擬合在多個領域都能夠很好地對非線性數據進行擬合分析，并得到令人滿意的結果，這說明曲線擬合具有良好的適配性和兼容性。

采用SPSS 26回歸分析中的曲線估算對昆明某選礦廠壓濾機的給礦壓濾、機械壓榨和空氣干燥階段的生產數據進行擬合分析，并求得各階段的最優工作時間。SPSS軟件中的曲線估算可以選擇合適的曲線模型對數據進行擬合，并通過最小二乘法得出擬合曲線的公式參數，具有較好的擬合精度。

2.1 機械壓榨擬合分析

由于給礦壓濾階段涉及的參數變量較多，先對壓榨階段進行工序時間優化分析。壓榨階段壓濾機各工作參數如表1所示。

共有12組實驗數據，每次實驗結果的測量時間間隔為10 s，其他條件均保持不變，具體實驗數據如表2所示。選擇合適的曲線模型進行擬合，結果如圖4所示。

經過多個曲線模型的比較，最后發現三次函數模型的擬合程度最優，并且從圖4可以看出最優的壓榨時間為130 s，為了進一步證明模型的可靠性，接下來對模型進行相關分析。

表1 壓榨階段壓濾機工作參數Table 1 Working parameters of filter press in press stage

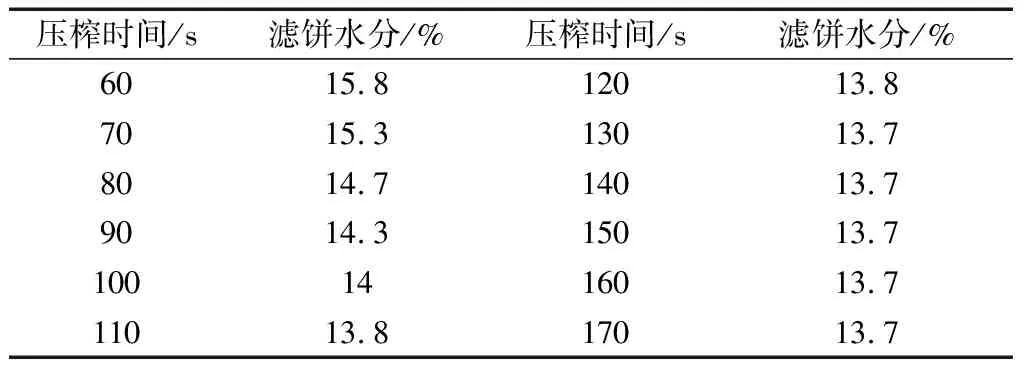
表2 壓榨階段濾餅水分實驗數據Table 2 Moisture test data of filter cake in pressing stage

圖4 壓榨階段擬合曲線Fig.4 Fitting curve at pressing stage

(1) 擬合優先度檢驗。擬合優先度檢驗是利用判定系數R2作為判斷依據，R2取值范圍是0～1，R2越接近1，則說明模型的擬合程度越好，反之，R2越接近0，則說明模型擬合效果越差，R2定義公式為

(3)

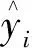
(2) 顯著性檢驗。顯著性檢驗是利用方差分析中統計量F及其sig.的大小進行分析判斷，F越大說明顯自變量對因變量的影響效果越大，F越顯著說明方程擬合約有意義，其公式為

(4)

式(4)中：k為自變量個數。

(3) 回歸系數檢驗。回歸系數檢驗是利用t檢驗統計量進行判斷，判斷方程系數是否具有統計學意義，其公式為

(5)

判定系數和F統計量如表3所示，由擬合結果可以得出，選擇三次方程模型擬合的R2為0.996，F為735.6且sig.=0<0.05，說明三次曲線對于壓榨階段濾餅水分隨時間的變化有較好的擬合效果；t檢驗結果如表4所示，由數據可知，三次曲線回歸擬合的系數都滿足sig.<0，說明回歸系數是顯著的，都具有統計學意義。

根據上述分析，可以認為利用三次曲線對壓榨階段的壓濾機工作情況進行擬合分析能夠得到精確的擬合結果，三次曲線公式一般形式為

y=ax+bx2+cx3+D

(6)

式(6)中：a、b、c和D均為參數。

(7)

(8)

最后，根據表4可以得到壓榨階段濾餅水分V(t)和壓濾時間t的擬合公式為

V(t)=-0.203t+0.001t2-

2.953×10-6t3+23.823

(9)

表3 壓榨階段判定系數R2和F統計量Table 3 R2 and F of pressing stage

表4 壓榨階段t檢驗Table 4 Student’s t test of pressing stage

2.2 空氣干燥擬合分析

空氣干燥擬合階段同樣采用控制變量的方法進行實驗，在其他條件不變的情況下記錄空氣干燥階段濾餅水分和空氣干燥時間的變化數據，壓濾機各工作參數如表5所示。

根據3.1節中的分析方法，對空氣干燥階段濾餅水分和時間之間的變化關系進行曲線擬合分析，工作數據共有12組，每隔20 s記錄一次實驗數據，具體內容如表6所示，選擇合適的曲線模型進行曲線擬合，經過多次模擬確定三次曲線模型的擬合程度最好， 得到的結果如圖5所示。

空氣干燥階段判斷系數R2和方差檢驗的F統計量如表7所示，其中R2=0.994，F=472.444且sig.=0<0.05，可以看出三次曲線能夠較好地模擬空氣干燥階段濾餅水分含量和空氣干燥時間的關系，并且可以看出最優的空氣干燥時間在160 s，此后濾餅水分基本不再改變。表8是空氣干燥階段的回歸系數t檢驗結果，從表7中可以看出各系數都滿足，說明系數是具有統計學意義的，擬合效果顯著。

表5 空氣干燥階段壓濾機工作參數Table 5 Working parameters of filter press in air drying stage

表6 空氣干燥階段濾餅水分實驗數據Table 6 Moisture test data of filter cake in air drying stage

圖5 空氣干燥階段擬合曲線Fig.5 Air drying stage fitting curve

表7 空氣干燥階段判定系數和F統計量Table 7 R2 and F of air drying stage

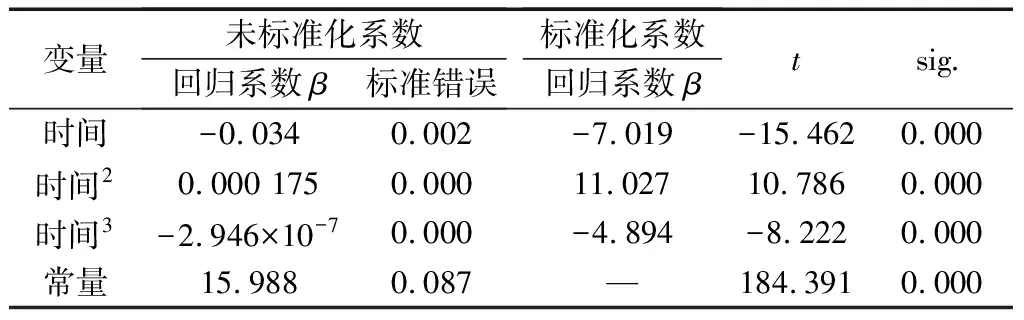
表8 空氣干燥階段t檢驗Table 8 Student’s t test of air drying stage

由表7的數據可知，空氣干燥階段濾餅水分和空氣干燥時間的擬合公式為

V(t)=-0.034t+0.000 175t2-

2.946×10-7t3+15.988

(10)

2.3 給礦壓濾擬合分析

給礦壓濾階段的工作時間長度決定了給礦量和濾餅最終厚度，因此該階段需要考慮濾餅厚度對單位時間處理量和濾餅最終含水量的多因素影響。進行實驗的礦漿濃度為53%，其余參數如表9所示。

該階段共有17組實驗數據，每組數據濾餅厚度增加1 mm，分別記錄各組給礦時間、濾餅厚度、單次處理量、周期、單位時間處理量和濾餅水分，詳細數據如表10所示，該階段主要考慮濾餅厚度對單位時間處理量和濾餅水分的影響進行分析。

表9 給礦壓濾階段壓濾機工作參數Table 9 Working parameters of filter press in delivering ore pressure filtration stage

表10 給礦壓濾階段實驗數據Table 10 Experimental data of delivering ore pressure filtration stage

2.3.1 濾餅厚度對單位時間處理量的影響分析

將濾餅厚度作為自變量，單位時間處理量作為因變量，選擇不同曲線模型進行曲線擬合，最終發現三次曲線擬合效果最好，并且可以看出濾餅厚度在30 mm時單位時間處理量最大。由于變量存在一定共線性，擬合結果剔除了一次變量，只保留二次和三次變量，擬合結果如圖6所示。

對濾餅厚度與單位時間處理量關系的擬合曲線進行相關分析。表11是其判斷系數R2和方差檢驗的F統計量的結果，其中R2=0.952，F=139.057，說明曲線擬合效果較好、擬合效果顯著。

表12是濾餅厚度與單位時間處理量關系的回歸系數t檢驗結果，從結果能夠看出，剔除了一次變量的回歸系數，各回歸系數和常量對應顯著性均小于0.05，可以認為回歸系數是顯著的。

從表12可以得出濾餅厚度與單位時間處理量關系的擬合公式為

y=0.018x2-0.003x3-8.169

(11)

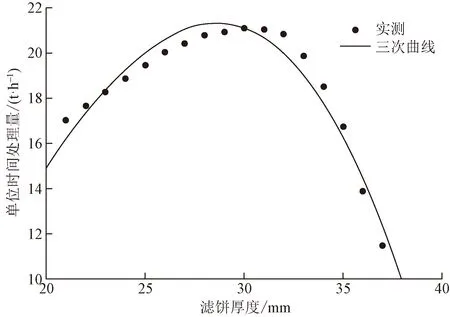
圖6 濾餅厚度與單位時間處理量關系Fig.6 Relationship between filter cake thickness and unit time processing capacity

表11 濾餅厚度與單位時間處理量關系的 判定系數和F統計量Table 11 R2 and F of relationship between filter cake thickness and unit time processing capacity

表12 濾餅厚度與單位時間處理量的t檢驗Table 12 Student’s t test of filter cake thickness and unit time processing capacity

式(11)中：x為濾餅厚度；y為單位時間處理量。

2.3.2 濾餅厚度對濾餅水分的影響分析

將濾餅厚度作為自變量，濾餅水分作為因變量進行曲線擬合，根據生產過程中的實際情況并結合生產數據選擇合適的曲線模型并對比擬合效果，最終選擇對數函數進行擬合，擬合結果如圖7所示。

從圖7可以看出，用對數函數對濾餅厚度和濾餅水分關系進行擬合效果較好，并且能夠反映實際生產中的變化趨勢。表13是判斷系數R2和方差檢驗的F統計量的結果，R2=0.843，F=80.735，說明曲線擬合效果尚可，能解釋因變量84.3%的變化。

表14是濾餅厚度與濾餅水分的回歸系數t檢驗結果，其中變量和常量的sig.都小于0.05，說明回歸系數顯著，具有統計學意義。

對數函數的公式為

y=B+blnx

(12)

將表14中數據代入式(12)得濾餅厚度y與濾餅水分x的回歸方程為

y=8.792+1.392lnx

(13)

圖7 濾餅厚度與濾餅水分關系Fig.7 Relationship between cake thickness and cake moisture

表13 濾餅厚度與濾餅水分的判定系數和F統計量Table 13 R2 and F of cake thickness and cake moisture

表14 濾餅厚度與濾餅水分關系t檢驗Table 14 Student’s t test of cake thickness and cake moisture

從上述擬合結果可以看出，在濾餅厚度為30 mm時單位時間處理能力最大，雖然濾餅水分隨著濾餅厚度的增加而增加，但是，綜合考慮單位時間處理能力和濾餅水分，在保證濾餅水分達標的情況下，最終確定最優濾餅厚度為30 mm，其對應工作時間為155 s。

3 實驗結果分析

從上面分析結果能看出來，無論是壓榨階段還是空氣干燥階段都存在一個最優的工作時間，若工作時間太短則會導致一部分濾餅水分沒有排出而達不到生產標準，若工作時間太長，雖然能夠保證最終水分能夠達標，但是繼續延長工作時間濾餅水分也不會再發生改變，這不利于提高生產效率和壓濾機的利用率，間接導致了生產成本的提高。

給礦壓濾階段要對工作時間進行優化，首先需要考慮濾餅厚度對單位時間處理量和濾餅水分的影響，在保證單位時間處理量最大的情況下確定濾餅厚度從而反推給礦壓濾階段的最優工作時間。

經過擬合分析得到的各階段最優工作時間與實際生產實驗得到的各階段最優工作時間如表15所示。

表15 優化工作時間與實際生產工作時間Table 15 Optimization of working hours versus actual productive working hours

從表15可以看出，壓榨階段和空氣干燥階段的最優工作時間擬合結果與實驗結果一致，而給礦壓濾階段的最優工作時間則存在一定誤差，原因如下：①曲線擬合只能在一定程度上實現數據的擬合分析，不能完全符合實驗數據的結果；②壓濾階段是以濾餅厚度為依據進行分組實驗，導致各組壓濾機的工作時間間隔較大，不能很好地對最優壓濾時間進行分析；③給礦壓濾階段曲線擬合的R2=84.3%，只能解釋因變量變化的84.3%，相比于機械壓榨階段的R2=0.994和空氣干燥階段的R2=0.952，擬合效果相對有所不足。

4 結論

采用統計分析軟件SPSS 26對昆明某礦的自動壓濾機生產數據進行曲線擬合分析，利用少量的實驗數據對壓濾機的給礦壓濾階段、機械壓榨階段和空氣干燥階段的生產數據進行了擬合分析以尋求最優工作時間，并得到了較為不錯的分析結果，同時得到了壓濾機3個工作階段的濾餅水分和工作時間的回歸方程，可以根據需要的濾餅水分調整各階段壓濾時間。最后，通過與實際生產情況對比，在一定程度上證明了統計分析軟件SPSS 26能夠對壓濾機的脫水工作流程進行優化分析，從而避免了繁瑣的仿真模型建立和大量的實驗過程。

采用統計分析方法對壓濾機的最優脫水工作時間進行相關分析，具有一定生產指導意義和研究價值，能夠為統計分析方法在選礦行業的應用提供參考價值。