基于BRGWO算法和濾波Smith預估器的氣彈系統(tǒng)時滯控制

李迺璐，范瑞杰，駱紫薇，曹智廣

(揚州大學 電氣與能源動力工程學院,江蘇 揚州 225100)

翼型氣彈系統(tǒng)廣泛存在于飛行器、風力機和直升機等,在實際氣彈控制系統(tǒng)不可避免的存在的時滯環(huán)節(jié)，如來自驅(qū)動器、閉環(huán)信號傳輸?shù)臅r滯等。一方面，氣彈系統(tǒng)工況通常較為復雜，存在風速不確定變化、負載干擾等；另一方面，氣彈系統(tǒng)的顫振特性對于系統(tǒng)參數(shù)變化較為敏感，嚴重時會在短時間內(nèi)極速惡化[1]。由于氣彈敏感性和工作環(huán)境復雜性, 時滯帶來的氣彈控制遲延，易導致顫振特性惡化,嚴重時會造成系統(tǒng)毀壞[2]。因此，需要研究在不確定工況下，可以克服時滯影響的氣彈系統(tǒng)控制方法，從而保證氣彈系統(tǒng)的安全高效運行。

目前，翼型氣彈系統(tǒng)最常應用的控制器為比例-積分-微分(proportional integral derivative,PID)控制器和線性二次型(linear quadratic regulator，LQR)控制器。PID 控制器由于結構簡單、可靠性高和應用性強，應用最廣泛。文獻[3]設計了PID控制器，有效減少了翼型氣彈系統(tǒng)的揮舞位移; 文獻[4]基于尾緣襟翼結構，利用PID控制器，實現(xiàn)了風力機葉片翼型的氣彈控制。 LQR控制器考慮了驅(qū)動限制問題，基于氣彈系統(tǒng)的狀態(tài)量設計狀態(tài)反饋控制器，可以在保證氣彈控制效果的同時進一步降低驅(qū)動器勞損[5]。近年，多種先進控制器方法應用于翼型氣彈系統(tǒng)控制，在多種工況下可以改善動態(tài)特性、提高氣彈控制的魯棒性。文獻[6]在風況下設計了預測控制振動器，有效減小了翼型揮舞和扭轉(zhuǎn)運動;文獻[7]利用魯棒控制器，在周期時變干擾下保持了良好的氣彈控制效果；文獻[8]設計了自適應內(nèi)模控制器，在多種不確定工況下增強了翼型氣彈控制的魯棒性。

上述文獻的氣彈控制器設計主要基于理想非時滯系統(tǒng)，并未充分考慮實際系統(tǒng)中可能存在的時滯環(huán)節(jié)及其影響。在不確定工況下，遲延的控制信號難以及時有效地控制氣彈系統(tǒng)，易會造成系統(tǒng)失穩(wěn)。因此，針對時滯和不確定工況，需要提高氣彈控制器的有效性和魯棒性，核心在于解決時滯下的氣彈控制問題。

針對系統(tǒng)時滯問題，Smith預估器在各類系統(tǒng)及工程問題中得到了廣泛的應用[9-12]但當系統(tǒng)或環(huán)境發(fā)生變化時，Smith預估器易存在預估模型失配的問題，導致其無法充分發(fā)揮時滯補償?shù)淖饔茫斐蓵r滯控制效果惡化，模型失配較大時甚至出現(xiàn)系統(tǒng)振蕩。 為此，國內(nèi)外學者提出了一系列針對Smith預估器的優(yōu)化方案。文獻[13]針對煉油控制時滯系統(tǒng)，設計了PI改進型Smith預估器控制結構，在系統(tǒng)變參數(shù)和干擾工況下明顯改善控制的魯棒性；文獻[14]針對工業(yè)對象滯后控制問題，將PI和PD作為主副控制器，提出了一種改進型Smith預估器結構，在模型失配嚴重時保持了較好的控制效果；文獻[15]利用一階濾波器設計Smith預估器，針對一階時滯穩(wěn)定系統(tǒng)、一階時滯不穩(wěn)定系統(tǒng)和多輸入多輸出不穩(wěn)定系統(tǒng)具有良好的控制性能。上述文獻研究大多針對具有較長時滯的工業(yè)過程，而翼型氣彈系統(tǒng)具有不確定小時滯、系統(tǒng)參數(shù)敏感、氣彈特性變化快和干擾多等特點，目前，針對這類系統(tǒng)的Smith預估器控制研究還較少。

Smith預估器的應用還依賴于選擇合適的控制參數(shù)。Smith預估控制參數(shù)的整定方法主要包括經(jīng)驗法[16-17]、神經(jīng)網(wǎng)絡算法[18-19]和智能優(yōu)化算法[20-21]等，其中，智能優(yōu)化算法由于智能化程度高、尋優(yōu)效果好和整定效率高受到關注。Mirjalili等[22]在2014年提出了一種灰狼優(yōu)化算法(grey wolf optimization, GWO)，該算法根據(jù)大自然中灰狼的等級制度，模擬灰狼合作捕獵行為，達到尋優(yōu)的目的。 相比傳統(tǒng)啟發(fā)式智能算法，GWO算法具有調(diào)整參數(shù)較少、結構簡單、易于實現(xiàn)和優(yōu)化性能好等特點。傳統(tǒng)GWO算法的尋優(yōu)結果與各等級狼的位置有極大關系，如果位置不理想，易陷入局部最優(yōu)和過早收斂。

為了有效實現(xiàn)時滯下的翼型氣彈系統(tǒng)控制，本文提出了一種基于雙向隨機灰狼優(yōu)化算法和濾波Smith預估器的時滯控制方法，該方法設計了改進型濾波Smith預估器控制器，設計了雙向隨機灰狼優(yōu)化算法，進行時滯下氣彈控制參數(shù)的全局尋優(yōu)，主要創(chuàng)新點包括以下3個方面：

(1)針對翼型氣彈系統(tǒng)的有界時滯，設計基于雙向隨機灰狼優(yōu)化算法和濾波Smith預估器的氣彈控制方法，在時滯和多工況下保持氣彈控制的良好動態(tài)特性；

(2)引入二階濾波器，改進傳統(tǒng)Smith預估器，增強時滯下的翼型氣彈控制性能、在不確定時滯、系統(tǒng)變參數(shù)和干擾下增強魯棒性和抗干擾能力；

(3)創(chuàng)新設計了雙向隨機灰狼優(yōu)化算法(bidirectional random grey wolf optimization，BRGWO)，來搜索時滯下氣彈控制器的全局最優(yōu)參數(shù)。 該算法通過改進不同社會等級灰狼的位置更新機制，增強狼群的多樣性，提高跳出不理想位置的幾率，避免陷入局部最優(yōu)，從而提高全局最優(yōu)值的尋優(yōu)質(zhì)量。

本文在通過以下算例對翼型氣彈控制進行研究，即不確定時滯、固定時滯下的不確定工況(風速變化、結構剛度變化和負載干擾)，將創(chuàng)新設計的BRGWO算法與傳統(tǒng)智能優(yōu)化算法進行對比，將本文方法與已有控制方法進行比較分析，驗證其優(yōu)越性和魯棒性。

1 雙向隨機灰狼優(yōu)化算法設計

1.1 傳統(tǒng)灰狼優(yōu)化算法

灰狼優(yōu)化算法GWO是一種啟發(fā)式種群智能優(yōu)化算法，靈感來自于灰狼種群的狩獵和社會等級行為。狼群分為不同等級的四類，其中：α狼擁有最高等級并領導整個狼群，β狼尊重α狼并領導δ狼和Ω狼，δ狼只領導Ω狼。在傳統(tǒng)灰狼優(yōu)化算法中，α狼、β狼和δ狼一起領導Ω狼的狩獵行為，即優(yōu)化過程。

灰狼種群的獵物包圍策略為

D=|CXj(t)-μjX(t)|

(1)

X(t+1)=Xj(t)-A·D

(2)

(3)

式中：Xj獵物矢量位置；X灰狼矢量位置；A和C為系數(shù)矢量；μj為狩獵策略因子向量；rand1和rand2為0～1的隨機向量；a為收斂因子；t為迭代次數(shù)；tmax為最大迭代次數(shù)。

α狼、β狼和δ狼的狩獵策略可表示為

(4)

1.2 雙向隨機灰狼優(yōu)化算法的創(chuàng)新設計

本文首次創(chuàng)新設計了一種改進型的灰狼優(yōu)化算法，即雙向隨機灰狼優(yōu)化算法，其引入狩獵策略因子μ，采用基于狩獵策略因子矢量和系數(shù)矢量的雙向隨機機制來改進α狼、β狼和δ狼的狩獵方式，使得社會等級較高的狼能夠跳出不理想的位置、尋找更多潛力位置，從而提高迭代后期的搜索能力、避免整個狼群陷入局部最優(yōu)、避免算法過早收斂。

利用狩獵策略因子，BRGWO算法的α狼、β狼和δ狼的改進型狩獵策略可表示為

(5)

(6)

式中：μα，μβ和μδ分別為α狼、β狼和δ狼的狩獵策略因子向量；Dα，Dβ和Dδ分別為α狼、β狼和δ狼的包圍步長向量；rand3，rand4和rand5為0～1的隨機向量。

BRGWO算法的灰狼種群位置更新公式表示為

(7)

(8)

相比傳統(tǒng)灰狼優(yōu)化算法，創(chuàng)新設計的BRGWO算法具有以下優(yōu)點：①利用式(7)～式(8)可對α狼、β狼和δ狼的狩獵策略進行不同程度的調(diào)節(jié)；②針對社會等級最高的α狼，采用較為保守的策略，在較小范圍內(nèi)增加狩獵包圍的多樣性；③針對社會等級第二優(yōu)和第三優(yōu)的狼，采用更加開放的策略，不斷擴大狩獵包圍的探索范圍；④利用系數(shù)矢量和狩獵策略因子向量的雙向隨機機制，及時跳出α狼、β狼和δ狼的不理想位置，增強搜索能力、避免過早收斂和陷入局部最優(yōu)。 BRGWO算法的流程如圖1所示。

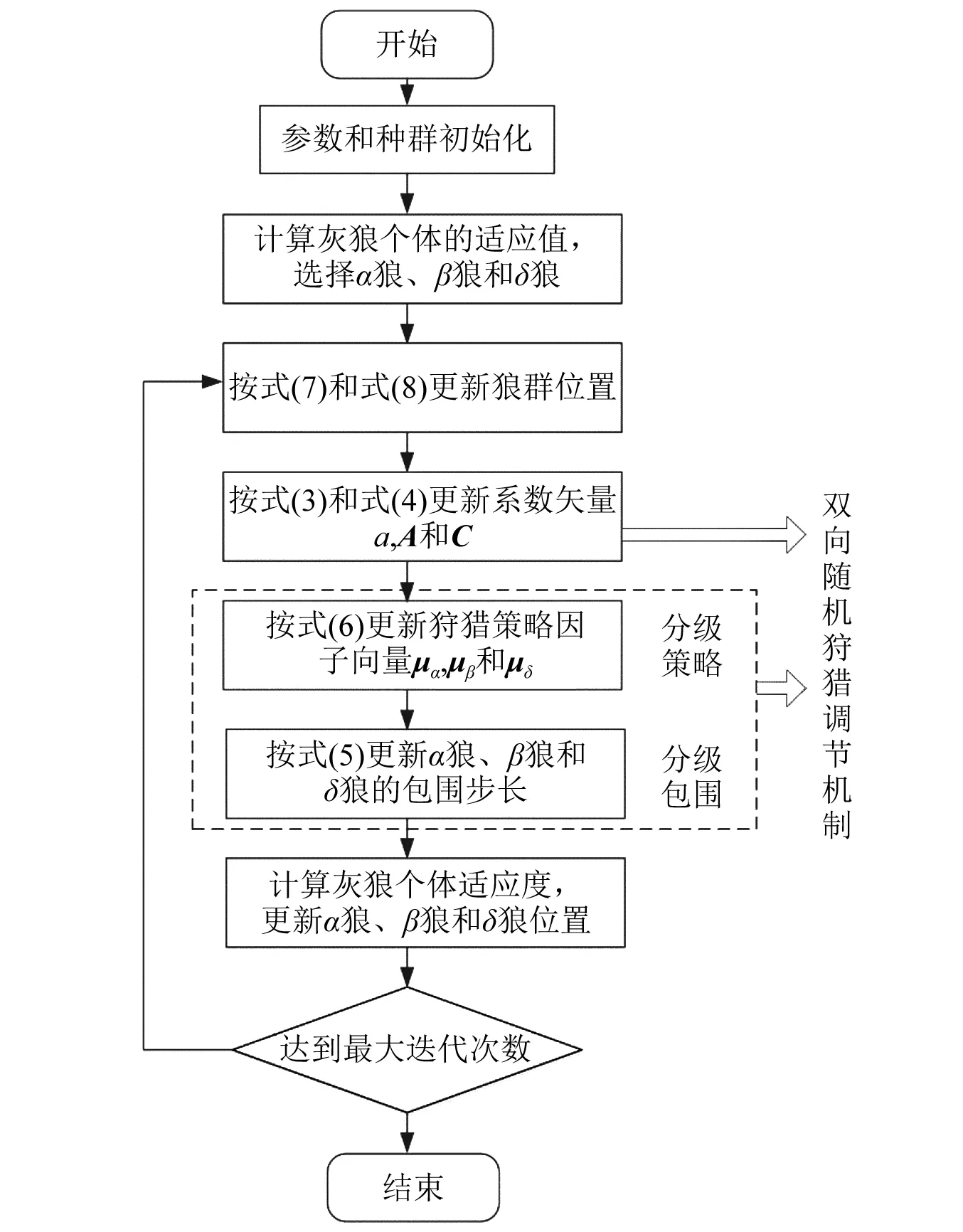
圖1 BRGWO算法流程圖Fig.1 Flow chart of BRGWO algorithm

2 翼型氣彈系統(tǒng)

翼型氣彈系統(tǒng)的結構示意如圖2所示，其中包括來流風速、氣動力、葉片彈性體和尾緣襟翼驅(qū)動器[23]，翼型氣彈系統(tǒng)的振動量為扭轉(zhuǎn)角α和揮舞位移h，c為翼型弦長，b為半弦長,ab為中心點到彈力軸的距離，在氣動力作用下的振動系統(tǒng)模型可表示為[24]

(9)

式中：mT為翼型氣彈系統(tǒng)和支撐部分總質(zhì)量；mW為翼型氣彈系統(tǒng)質(zhì)量；xa為質(zhì)心和彈性軸之間無量綱距離；Iα為彈性軸轉(zhuǎn)動慣量；ch,cα為阻尼系數(shù)；kh,kα為結構剛度系數(shù)；L,M分別為氣動升力和氣動力矩。

考慮定常氣動力、振動位移以及尾緣襟翼驅(qū)動器對氣動升力的影響，氣動升力可表示為

(10)

式中：U為來流風速；clα為葉片攻角對應的氣動升力系數(shù)；clβ為尾緣襟翼對應的氣動升力系數(shù)。

考慮定常氣動力、振動量以及尾緣襟翼驅(qū)動器對氣動力矩的影響，翼型氣彈系統(tǒng)承受的氣動力矩可表示為

(11)

式中：cmα為攻角對應的氣動力矩系數(shù)；cmβ為尾緣襟翼對應的氣動力矩系數(shù)。

聯(lián)合式(9)～式(11)，翼型氣彈系統(tǒng)的氣動彈性模型可表示為

(12)

(13)

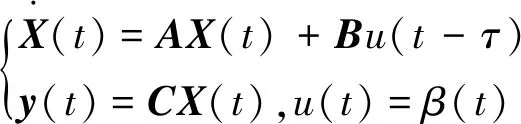
(14)

式中：控制量u為尾緣襟翼角β；τ為不確定時滯時間。本文控制目標為利用尾緣襟翼實現(xiàn)翼型氣彈系統(tǒng)的扭轉(zhuǎn)角和揮舞位移控制，根據(jù)經(jīng)驗，采用扭轉(zhuǎn)角作為有效反饋量來實現(xiàn)控制目標。翼型氣彈系統(tǒng)參數(shù)見Strganac等的研究。

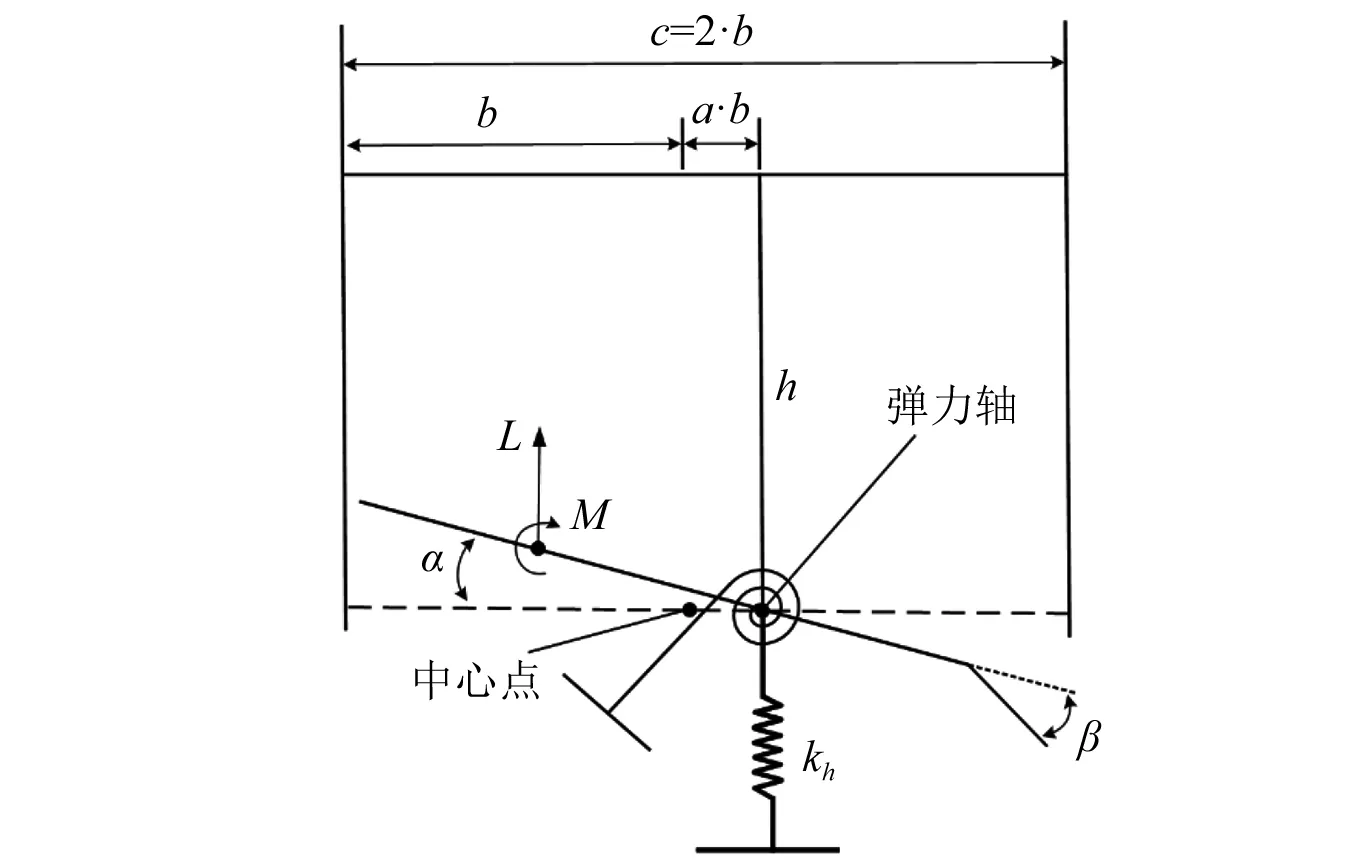
圖2 翼型氣彈模型示意圖Fig.2 Diagram of airfoil aeroelastic system

3 最優(yōu)濾波Smith預估器設計

3.1 傳統(tǒng)Smith預估器

傳統(tǒng)Smith預估補償器主要通過與控制器并聯(lián)的補償環(huán)節(jié)來補償滯后時間，原理如圖3所示[23]。

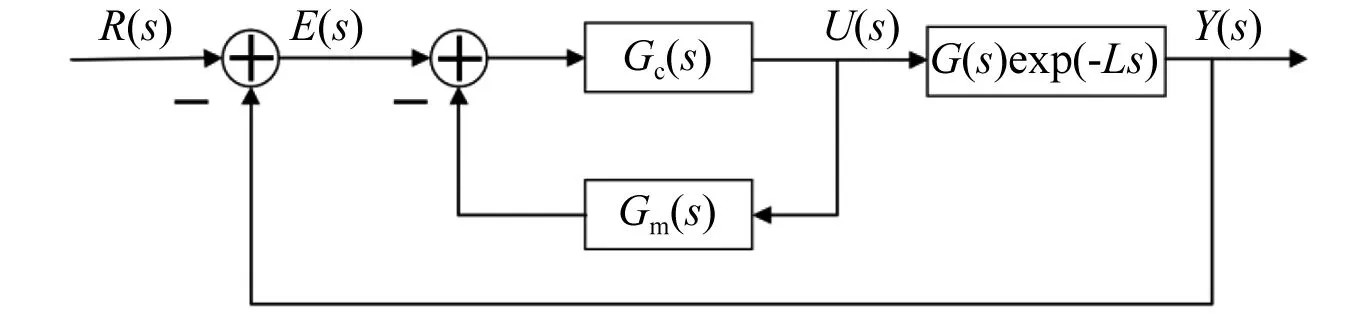
圖3 標準Smith預估控制原理圖Fig.3 Diagram of standard Smith predictive control

為了克服時滯環(huán)節(jié)exp(-Ls)的影響，控制結構中添加Gm(s)環(huán)節(jié)，對應閉環(huán)系統(tǒng)的特征方程可表達為

1+Gc(s)[Gm(s)+G(s)exp(-Ls)]=0

(15)

式中：G(s)為被控對象；Gc(s)為主控制器；Gm(s)為Smith預估補償器。令Gm(s)=G(s)[1-exp(-Ls)] ，式(15)為

1+Gc(s)G(s)=0

(16)

由式(16)可知，經(jīng)過時滯補償后，由于exp(-Ls)在整個閉環(huán)特征方程之外，不會影響到系統(tǒng)穩(wěn)定性，從而消除了滯后影響。但是，實際風力機葉片振動系統(tǒng)存在風速、剛度等不確定參數(shù)變化、時滯時間變化和負載干擾等影響，會使得G(s)和L發(fā)生不確定變化，導致模型失配；而傳統(tǒng)Smith預估器對被控對象模型精度有較高要求，在模型失配下易嚴重的動靜態(tài)誤差，甚至使閉環(huán)系統(tǒng)變得非常不穩(wěn)定，導致系統(tǒng)振蕩；同時，翼型氣彈系統(tǒng)由于本身顫振特性對于系統(tǒng)參數(shù)變化較為敏感，動態(tài)特性容易惡化，需要及時有效地克服模型失配并實現(xiàn)振動控制。

3.2 最優(yōu)改進型濾波Smith預估器設計

針對不確定時滯和多變工況下的翼型氣彈系統(tǒng)控制問題，設計基于二階魯棒濾波器的Smith預估控制，控制框圖如圖4所示。 其中：P(s)為控制對象；Gc(s)為主控制器；Gm(s)為Smith預估補償器；F(s)為魯棒濾波器；exp(-Lms)為純滯環(huán)節(jié)；Y(s)為系統(tǒng)輸出；R(s)為參考值；D(s)為驅(qū)動負載干擾。

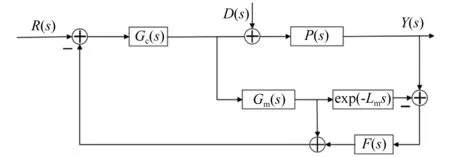
圖4 濾波Smith預估控制結構圖Fig.4 Diagram of filtered Smith predictive control

考慮翼型氣彈系統(tǒng)中存在的有界時滯和不確定工況影響，被控對象可表示為

(17)

式中：ΔG為風力機工況下失配模型；ΔL為時滯變化量。

根據(jù)圖4可知，單輸入單輸出閉環(huán)系統(tǒng)的傳遞函數(shù)可表示為

(18)

式中，Pm(s)=Gm(s)exp(-Lms)為理想系統(tǒng)模型。

針對翼型氣彈系統(tǒng)，設計主控制器Gc(s)為PID控制器

(19)

傳統(tǒng)方法多采用一階濾波器，本文基于濾波參數(shù)λ，設計二階魯棒濾波器為

(20)

(1)當無系統(tǒng)變化、無時滯時間變化時，存在G(s)=Gm(s)，L=Lm，即P(s)=Pm(s)，由式(9)可知，閉環(huán)系統(tǒng)的特征方程可簡化為

1+Gc(s)Gm(s)=0

(21)

(2)當存在不確定時滯和不確定系統(tǒng)參數(shù)變化的工況下時，G(s)≠Gm(s)，L≠Lm，即P(s) ≠Pm(s)。 根據(jù)式(9)，閉環(huán)系統(tǒng)的特征方程可表示為

1+Gc(s)Gm(s)+Gc(s)F(s)[G(s)e-Ls-Gm(s)e-Lms]=0

(22)

利用式(20)，設計濾波Smith預估器為

(23)

將式(17)代入式(23)，濾波Smith預估器可變?yōu)?/p>

(24)

將式(23)代入式(22)，得閉環(huán)系統(tǒng)特征方程

1+Gc(s)G(s)=0

(25)

由式(21)和式(25)可知，根據(jù)設計的主控制器和濾波Smith預估器，在理想情況、時滯變化和多變工況下可在閉環(huán)系統(tǒng)的特征方程中消除時滯環(huán)節(jié)，從而消除時滯對翼型氣彈控制系統(tǒng)的影響。式(23)和式(24)可知，所設計濾波Smith預估器可以針對模型失配和時滯變化利用魯棒濾波器F(s)進行控制。通過獲取主控器參數(shù)和濾波參數(shù)的最優(yōu)值，可以最大程度上優(yōu)化不確定時滯和工況下的振動控制效果。

(3)驅(qū)動負載干擾對系統(tǒng)輸出影響的傳遞函數(shù)可表示為

(26)

高階翼型氣彈系統(tǒng)可等效為二階阻尼系統(tǒng)

(27)

式中，a2，a1，a0，b1，b0為傳遞函數(shù)系數(shù)，均為正值。

將式(19)和式(20)和式(27)代入式(28)，整理后可得負載干擾下的閉環(huán)系統(tǒng)特征方程

(λs+1)2[(a2+kdb1)s2+(a1+kpb1-kdb0)s+

(a0-kpb0+kib1)]=0

(28)

由式(28)可知，通過選擇合適的主控器參數(shù)(kp，ki，kd)可以保證干擾下的閉環(huán)系統(tǒng)穩(wěn)定性；通過設計合適的濾波參數(shù)λ可進一步優(yōu)化時滯氣彈控制的動態(tài)特性和抗擾性能。

3.3 閉環(huán)穩(wěn)定性證明

利用最小增益原理，對所設計閉環(huán)系統(tǒng)的穩(wěn)定性進行證明。假設無時滯的翼型氣彈系統(tǒng)G(s)為穩(wěn)定系統(tǒng)，主控制器Gc(s)和濾波器F(s)也保持穩(wěn)定。 圖3中閉環(huán)系統(tǒng)具有穩(wěn)定性的充分必要條件為

|Gc(s)|H+|Gc(s)||F(s)||ΔP(s)|<1

(29)

式中：ΔP(s)為模型失配；H為模型失配的上界。

|ΔP(s)|=|P(s)-Pm(s)|<1

(30)

根據(jù)式(19)和式(20)，存在

|Gc(s)|<‖Gc(s)‖∞,|F(s)|<‖F(xiàn)(s)‖∞

(31)

將式(30)和式(31)代入式(29)，整理后可得

‖Gc(s)‖∞|ΔP(s)|(1+|F(s)|)<1

(32)

式(32)可進一步整理為

(33)

由式(33)可知，當翼型氣彈系統(tǒng)的模型失配上界為1/[‖Gc(s)‖∞(1+‖F(xiàn)(s)‖∞)]時，所設計基于濾波Smith預估器的閉環(huán)控制系統(tǒng)具有穩(wěn)定性。

推論1當系統(tǒng)參數(shù)變化，時滯時間不變時，存在G(s)≠Gm(s)，L=Lm，模型失配可表示為ΔP(s)=[G(s)-Gm(s)]e-Ls=ΔG(s)e-Ls，代入式(33)可得系統(tǒng)參數(shù)變化下的閉環(huán)系統(tǒng)穩(wěn)定條件為

(34)

推論2當時滯時間變化，系統(tǒng)參數(shù)不變時，存在G(s)=Gm(s)，L≠Lm，模型失配ΔP(s)可表示為

ΔP(s)=G(s)(e-Ls-e-Lms)≈
G(s)(Lm-L)s=G(s)ΔLs

(35)

代入式(33)可得時滯時間變化下的閉環(huán)系統(tǒng)穩(wěn)定條件為

(36)

3.4 時滯下最優(yōu)氣彈控制參數(shù)整定

針對基于改進型濾波Smith預估器的翼型氣彈控制器，利用所設計的BRGWO算法計算最優(yōu)控制參數(shù)，獲取最優(yōu)氣彈控制器，在不確定時滯、不確定風速、剛度變化和驅(qū)動干擾4種算例下進行控制試驗。控制參數(shù)優(yōu)化計算的目標函數(shù)為

(37)

氣彈控制器參數(shù)kp,ki,kd,μ取值范圍分別為[-50，0]，[-50，0]，[-10，0]和[0，2]。襟翼角的限制為[-60°，60°],時滯時間不超過3 s。灰狼種群規(guī)模30，最大迭代次數(shù)30。為了驗證所設計BRGWO算法的優(yōu)越性，采用遺傳算法(genetic algorithm,GA)和灰狼優(yōu)化算法進行對比試驗，為了公平起見，GA算法和GWO算法的種群規(guī)模和最大迭代次數(shù)也為30。目標函數(shù)的適應度值優(yōu)化結果如圖5所示。可見，GA和GWO容易陷入局部最優(yōu)，而BRGWO算法顯著改善了控制參數(shù)的全局尋優(yōu)性能、具有更快的收斂性，有效避免了局部最優(yōu)。基于BRGWO算法和濾波Smith預估器的翼型氣彈系統(tǒng)控制結構如圖6所示。

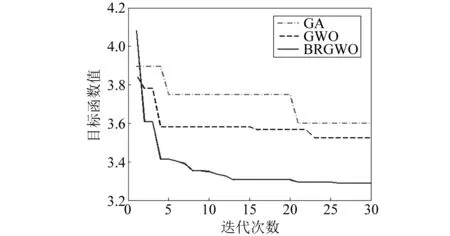
圖5 目標函數(shù)的適應度值Fig.5 Fitness value of objective function

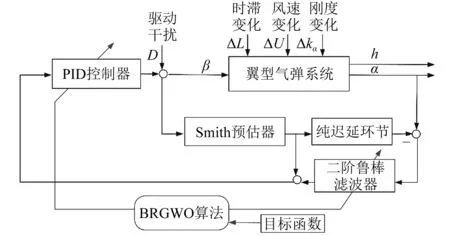
圖6 基于BRGWO算法和濾波Smith預估器的翼型氣彈系統(tǒng)控制結構圖Fig.6 Control structure of aeroelastic system based on BRGOW algorithm and filtered Smith predictor

4 仿真算例

本文采用所設計的BRGWO算法和改進型濾波Smith預估器，應用于不確定時滯下的翼型氣彈控制、以及多工況下的翼型時滯氣彈控制研究。翼型氣彈系統(tǒng)參數(shù)參見文獻[26]。系統(tǒng)時滯為1 s，選擇風速值U=6 m/s，剛度參數(shù)kα=2.82 N/m，kh=2 844.4 N/m。仿真在2.9 GHz IntelR CoreTMi7 CPU和16 GB RAM配置的計算機上執(zhí)行，仿真采用MATLAB/Simulink 2020a環(huán)境。 為了研究本文方法 (BRGWO-MF-Smith)，對比了GWO優(yōu)化的經(jīng)典Smith預估控制(GWO-Smith)、GWO優(yōu)化的PI-PD型Smith預估控制(GWO-PIPD-Smith)、GWO優(yōu)化的一階濾波Smith預估控制(GWO-F-Smith)。各控制器參數(shù)的優(yōu)化計算結果如表1所示，氣彈控制效果如圖7所示。可見，已有經(jīng)典Smith預估控制和傳統(tǒng)GWO算法難以克服時滯的不利影響，氣彈控制響應存在較大超調(diào)量、較長穩(wěn)定時間，尾緣襟翼的驅(qū)動勞損也較大；而本文提出的改進型濾波Smith預估器和BRGWO算法，顯著改善了系統(tǒng)超調(diào)量、穩(wěn)定時間和驅(qū)動勞損，在4個控制器中具有優(yōu)越性。

表1 各控制器的最優(yōu)控制參數(shù)

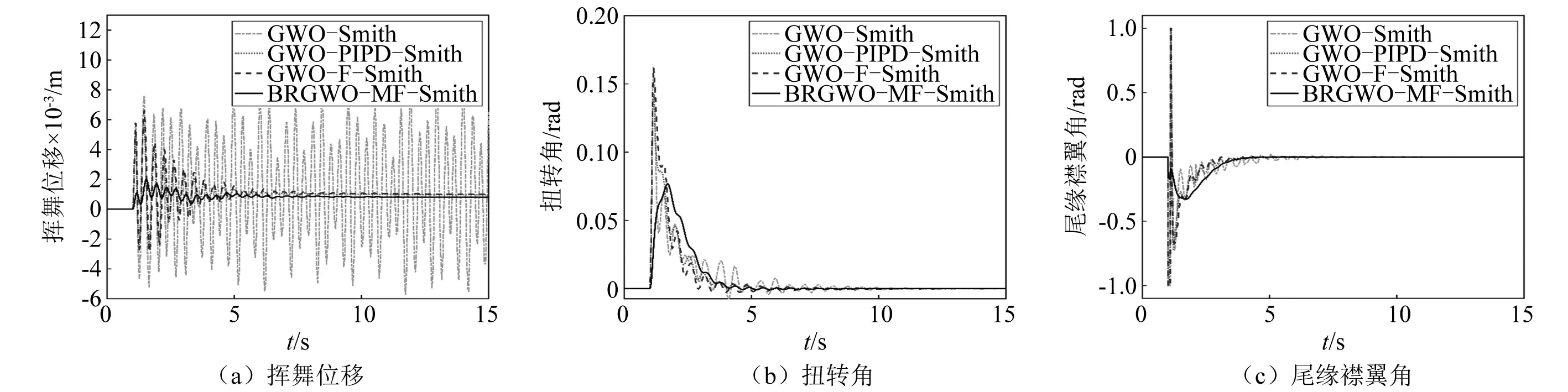
圖7 翼型時滯氣彈控制效果Fig.7 Delayed aeroelastic control

4.1 不確定時滯下氣彈控制

為了研究不確定時滯下的翼型氣彈控制效果，針對時滯時間+20%，+50%的兩種案例進行了試驗，翼型時滯氣彈控制效果如圖8和圖9所示。可見，GWO-Smith難以適應時滯時間的不確定變化，存在控制性能急劇惡化及系統(tǒng)失穩(wěn)現(xiàn)象；GWO-PIPD-Smith和GWO-F-Smith可在不確定時滯下保持系統(tǒng)的穩(wěn)定性，但存在較大超調(diào)量或較長穩(wěn)定時間。然而，本文提出的BRGWO-MF-Smith時滯氣彈控制方法，在不確定時滯下，顯著減小了超調(diào)量、縮短了穩(wěn)定時間、降低了襟翼控制成本，對比其他3種方法在不確定時滯下具有較強的魯棒性。

圖8 時滯時間+20%下的翼型氣彈控制效果Fig.8 Delayed aeroelastic control under delay time+20%

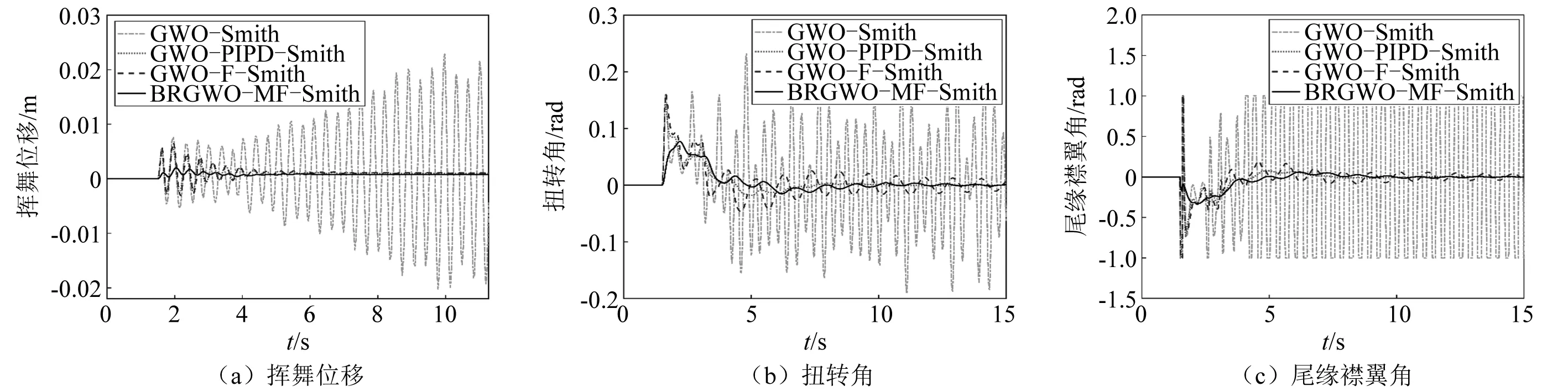
圖9 時滯時間+50%下的翼型氣彈控制效果Fig.9 Delayed aeroelastic control under delay time+50%

4.2 不確定風速下時滯氣彈控制

為了驗證本文方法在不確定風速下的時滯氣彈控制效果，分別研究了風速變化+20%和-20%的工況，系統(tǒng)時滯時間為1 s，時滯氣彈控制響應如圖10和圖11所示。可見，出現(xiàn)較大風速時，GWO-Smith無法在短時間內(nèi)實現(xiàn)氣彈控制。然而，相比GWO-PIPD-Smith和GWO-F-Smith，本文方法可以最小超調(diào)量和最少振蕩來實現(xiàn)氣彈系統(tǒng)的顫振抑制，針對風速變化保持了良好的時滯氣彈控制效果。 仿真結果說明了不確定風況下BRGWO-MF-Smith在4種控制器中具有最強的時滯氣彈控制效果和魯棒性、以及最小的驅(qū)動勞損。

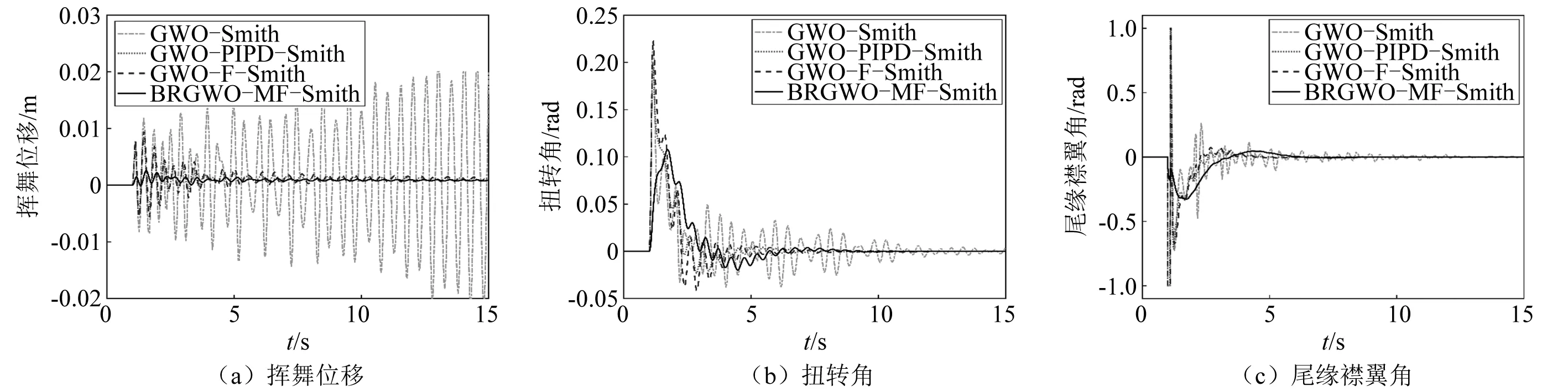
圖10 風速+20%下的翼型時滯氣彈控制效果Fig.10 Delayed aeroelastic control under wind velocity+20%

4.3 剛度變化下時滯氣彈控制

為了驗證本文方法在系統(tǒng)剛度參數(shù)變化下的有效性，分別研究了揮舞剛度和扭轉(zhuǎn)剛度+20%和-20%兩種案例,時滯氣彈控制響應如圖12和圖13所示,氣彈系統(tǒng)對剛度變化較為敏感，在此情況下，GWO-Smith無法保證系統(tǒng)的穩(wěn)定性、難以實現(xiàn)有效的氣彈控制；PIPD-Smith的超調(diào)量較大、GWO-F-Smith的穩(wěn)定時間較長；而本文設計的BRGWO-MF-Smith方法明顯改善了超調(diào)量、大幅縮減了穩(wěn)定時間，在不同剛度變化下保持了良好的魯棒性和較小的驅(qū)動勞損。因此，本文方法具有最佳的翼型時滯氣彈控制性能。

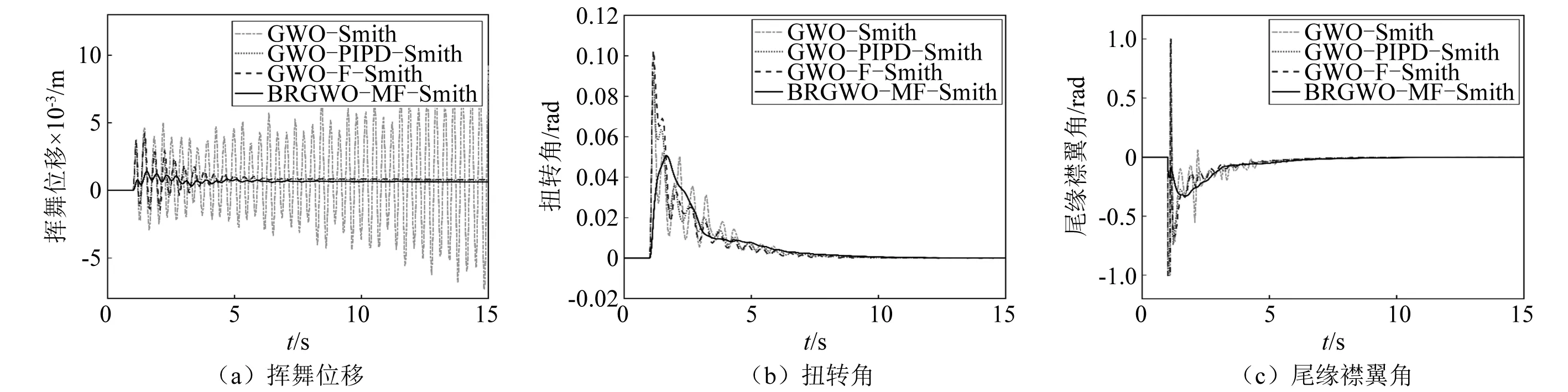
圖11 風速-20%下的翼型時滯氣彈控制效果Fig.11 Delayed aeroelastic control under wind velocity-20%

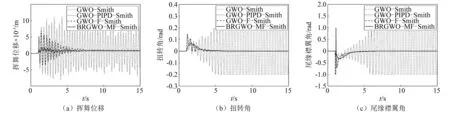
圖12 剛度+20%下的翼型時滯氣彈控制效果Fig.12 Delayed aeroelastic control under stiffness+20%

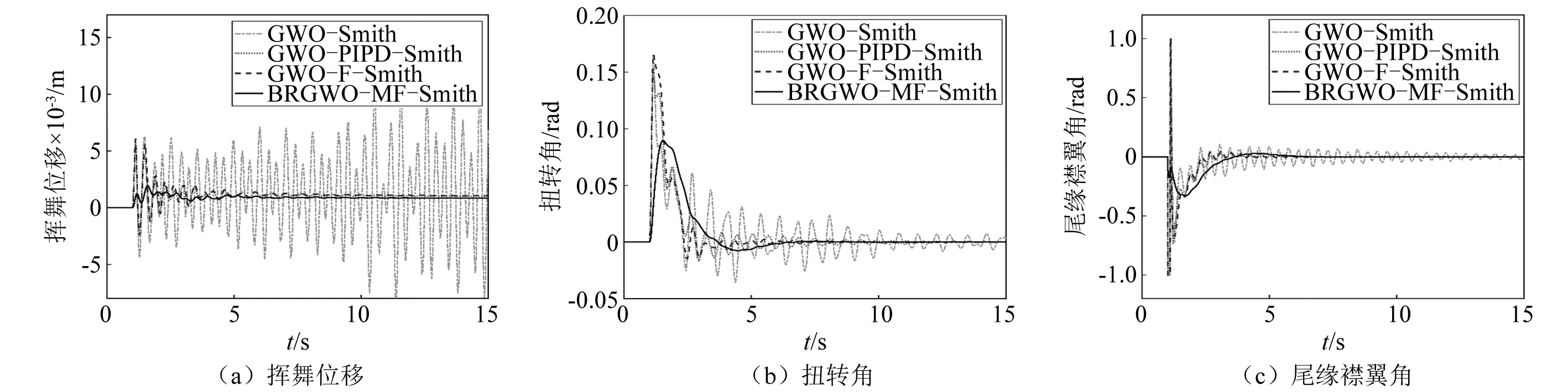
圖13 剛度-20%下的翼型時滯氣彈控制效果Fig.13 Delayed aeroelastic control under stiffness-20%

4.4 驅(qū)動干擾下時滯氣彈控制

在實際中還需要考慮來自驅(qū)動器的負載干擾，在6 s處加入驅(qū)動負載干擾信號，干擾下的翼型時滯氣彈控制響應如圖14所示。可見，4種控制器都可以克服驅(qū)動干擾，但GWO-Smith仍無法在短時間完全抑制系統(tǒng)顫振，PIPD-Smith和GWO-F-Smith存在較大超調(diào)量尖峰和較多振蕩。對比這些控制器，本文BRGWO-MF-Smith方法的時滯氣彈控制具有最佳動態(tài)性能、更優(yōu)越的抗擾性能和襟翼驅(qū)動性能。

4.5 定量分析

針對4種氣彈控制方法，表2和表3分別給出了7種算例下?lián)]舞位移和扭轉(zhuǎn)角的絕對誤差積分指標(integral of absolute error，IAE)。 可知，本文方法在所有7種算例下均具有最小的揮舞位移IAE值和扭轉(zhuǎn)角IAE值。在時滯+50%算例下，BRGWO-MF-Smith控制下的扭轉(zhuǎn)角和揮舞位移IAE值，對比GWO-Smith控制改善了86.5%和90.9%，對比PIPD-Smith控制改善了10.1%和26%，對比GWO-F-Smith控制改善了51%和31%；在風速+20%算例下，本文BRGWO-MF-Smith的揮舞位移IAE值，對比GWO-Smith，PIPD-Smith和GWO-F-Smith，分別改善了90.2%，33.9%和39.7%；在剛度-20%算例下，對比3種已有控制器的扭轉(zhuǎn)角IAE值分別改善了43.5%，26.6%和23%; 在干擾算例下，改善了3種已有控制器的揮舞位移IAE值得分別為57.3% 26.5%和30.4%。這得益于本文創(chuàng)新設計的BRGWO算法和改進型濾波Smith預估器，針對氣彈系統(tǒng)具有更為優(yōu)良的時滯控制補償效果、可有效尋找全局最優(yōu)的時滯氣彈控制參數(shù)。

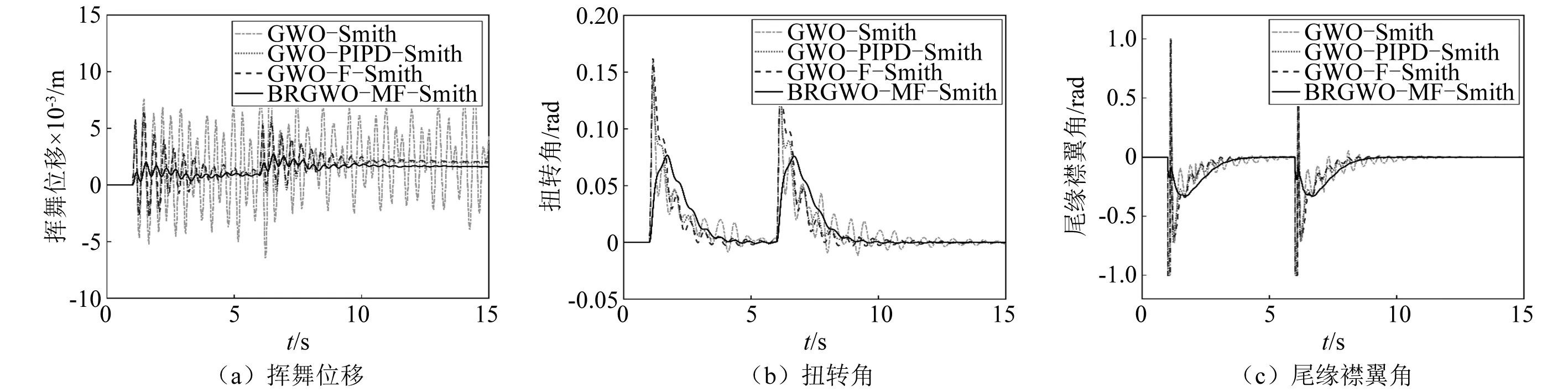
圖14 驅(qū)動負載干擾下的翼型時滯氣彈控制效果Fig.14 Delayed aeroelastic control under load disturbance

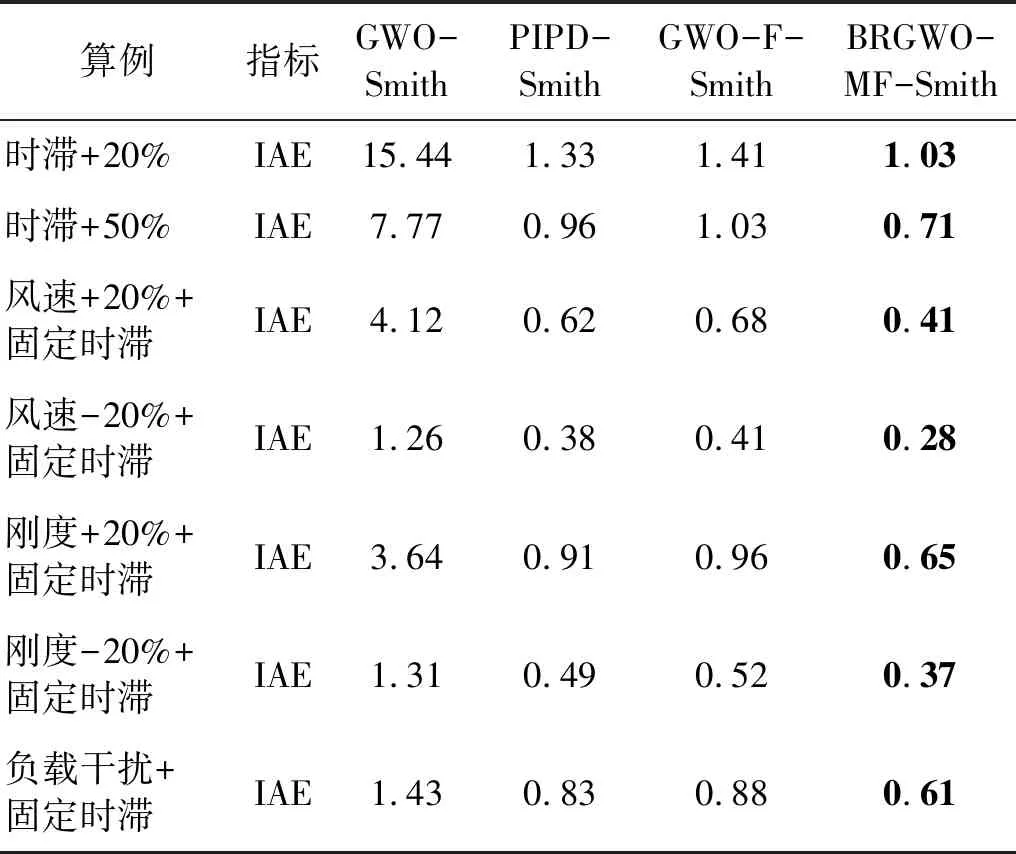
表2 7種算例下翼型時滯氣彈控制的揮舞位移IAE性能指標

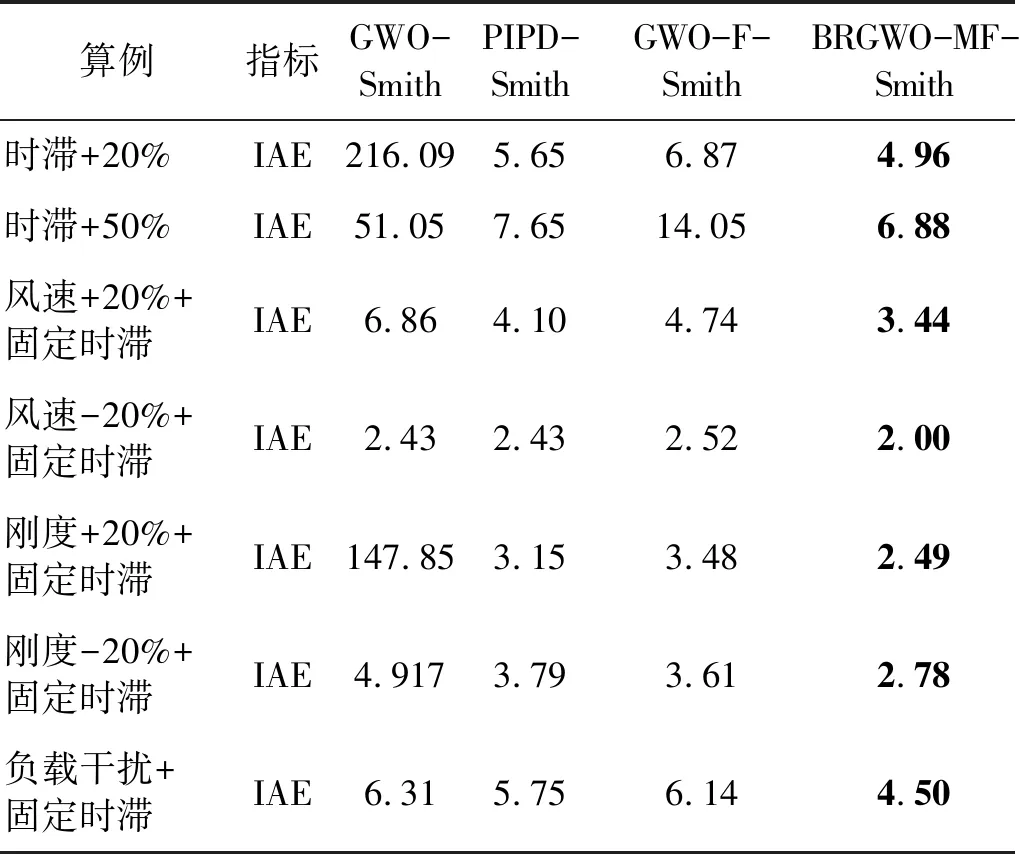
表3 7種算例下翼型時滯氣彈控制的扭轉(zhuǎn)角IAE性能指標

5 結 論

本文設計了基于二階濾波Smith預估器的翼型時滯氣彈控制結構，利用本文創(chuàng)新設計的雙向隨機灰狼優(yōu)化算法尋找全局最優(yōu)控制參數(shù)，在不確定時滯和多種工況算例下取得了良好的時滯補償效果和氣彈控制效果。主要結論歸納為以下3個方面:

(1)基于Smith預估控制理論，構建了時滯下翼型氣彈系統(tǒng)的控制器，引入二階魯棒濾波器改進Smith控制結構，增強了不確定時滯下氣彈控制的動態(tài)性能和魯棒性。

(2)基于分級制定包圍狩獵策略的思想，創(chuàng)新設計了雙向隨機灰狼優(yōu)化算法，避免了陷入局部最優(yōu)、增強了全局最優(yōu)值的搜索能力、加快了收斂速度，提高了翼型時滯氣彈控制參數(shù)的全局尋優(yōu)能力。

(3)仿真結果表明，基于BRGWO算法和改進型濾波Smith的翼型最優(yōu)氣彈控制器，對比已有算法及控制方法，在不確定時滯下顯著改善了氣彈控制效果，在不確定風速、剛度變化和驅(qū)動干擾下，具有優(yōu)越的是時滯補償能力和氣彈控制性能，魯棒性較強。