ECC沖擊壓縮力學特性及耗能機制的試驗研究

羅銀劍，李秀地，蔡 濤，楊謹鴻

(中國人民解放軍陸軍勤務學院 軍事設施系，重慶 401331)

軍事防護掩體一般都是由鋼筋混凝土構筑。厚重的鋼筋混凝土對于保護掩體內的人員和重要設備免遭武器破壞效應的毀傷是必要的。然而，在精確制導武器爆炸沖擊作用下，鋼筋混凝土結構內會產生高強度脈沖應力波傳播。應力波在混凝土的內表面反射產生拉伸波，能夠引起鋼筋混凝土結構內表面廣泛的剝落震塌。震塌產生的混凝土碎塊高速飛離，對掩體內的人員和裝備構成威脅[1]。因此，采用普通混凝土作為建筑材料的防護結構，難以滿足對新型大威力精確制導武器的防護要求。

眾多研究者圍繞發展新型防護材料展開研究。20世紀90年代，美國密歇根大學Li等[2-3]運用斷裂力學和細觀力學原理，將聚乙烯短切纖維(簡稱PE纖維)經過特殊處理，加入水泥基復合材料中，通過試驗發現該材料在受到拉應力時能夠形成多個裂縫，極限應變大幅提高，混凝土表現出較高韌性，他們將這種具有明顯應變硬化和多縫開展特征的新型纖維混凝土材料命名為工程水泥基復合材料(engineered cementitious composite，ECC)。這一新材料的出現，引起國內外建筑材料領域學者的濃厚興趣，對工程水泥基復合材料的靜態力學性能以及所用的纖維材料進行深入研究，相繼發展出聚丙烯纖維ECC(polypropylene engineering cementitious composite，PP-ECC)、聚乙烯醇纖維ECC(polyvinyl alcohol engineering cementitious composite，PVA-ECC)以及混合纖維ECC等眾多改進型ECC。由于PVA纖維力學性能較好，成本相對便宜，國內生產的ECC大多采用PVA纖維。

ECC優異的吸能特性，在抗爆抗沖擊方面有一定的應用潛力，吸引越來越多的學者對ECC的動力學性質展開研究。陳智韜等[4-5]采用Φ40 mm分離式霍普金森壓桿 (split Hopkinson pressure bar, SHPB) 試驗研究了礦渣系和粉煤灰系兩種礦物摻合料的PVA-ECC在不同應變率下的動態壓縮性能，得出在兩者摻量相同的情況下礦渣系PVA-ECC的應變率效應更加顯著的結論。張華等[6]利用大尺寸變截面Φ74 mm SHPB裝置對不同摻量的聚乙烯工程水泥基符合材料(polyethylene engineering cementitious composites，PE-ECC)進行沖擊壓縮試驗，結果表明，當PE纖維摻量在1.8%時，PE-ECC的應變率效應顯著增強。杜修力等[7]重點研究了PVA纖維摻量對PVA-ECC動態壓縮峰值應變的影響，研究表明，峰值應變隨著PVA纖維含量的增加而增大，當纖維摻量達到一定數值后，極限應變不再增大，動態抗壓強度也無明顯變化。為了進一步提高ECC的動態抗壓強度，同時保持ECC高韌性的特點，Zhang等[8]利用鋼纖維彈性模量較大的優勢，在ECC中摻入0.6%的鋼纖維并進行ECC板的子彈沖擊試驗，結果表明，改進型ECC能有效削弱震塌損害，在子彈沖擊后板背部的彈坑最大直徑僅為普通混凝土產生碎片面積的60%。除了采用混合纖維來提高ECC的動態性能以外，Yildirim等[9]研究了在基體材料配比相同的情況下，體積分數同為2%的PVA-ECC和尼龍N纖維-ECC梁彎曲韌性和抗沖擊效果，試驗結果顯示，兩者的動態抗壓強度相當，PVA-ECC韌性表現稍強于尼龍N纖維-ECC，但尼龍N纖維價格便宜，有望成為PVA纖維的替代品。

以上研究表明，ECC最突出的優勢是在較高應變率下具有很好的韌性。目前，對ECC動態性質的研究主要集中在ECC動態抗壓強度、應變率效應方面，對ECC的耗能機理研究較少，尤其是ECC在沖擊作用下破壞形態與耗能能力之間的關系方面研究較為匱乏。為此，本文采用Φ50 mm的SHPB裝置重點研究了纖維摻量對ECC抗壓強度、破壞形態及耗能能力的影響，為今后ECC在抗爆抗沖擊方面的應用提供有價值的參考。

1 試驗概況

1.1 原材料及試件制備

本次試驗中的膠凝材料為P.O.42.5級的普通硅酸鹽水泥和I級低鈣粉煤灰，細骨料為特細河砂，平均粒徑不超過0.25 mm，添加劑采用高效聚羧酸減水劑，纖維為日本可樂麗公司生產的KURALONTMK-Ⅱ纖維(新型PVA纖維)，纖維表面經過涂油處理[10]，滿足與基體材料的黏結性能，基本物理參數如表1所示。

表1 PVA纖維基本物理參數Tab.1 Basic physical parameters of PVA fiber

Li等在ECC基體材料配合比方面作出開創性貢獻并進行了大量試驗，本文所制備的試件的基體材料配合比依據Li等提出的ECC基體材料的配合比，如表2所示。在試件纖維體積摻量設計方面，依據文獻[11]改進PVA纖維橋接模型得出的臨界體積摻量，設計試件纖維體積摻量為0，0.50%，1.25%，2.00%，2.30%。

表2 PVA-ECC配合比Tab.2 PVA-ECC mix ratio 單位：kg/m3

采用外徑Φ50 mm、內徑46 mm、長30 mm的PVC管具作為試件模具，試件經標準條件下養護28 d后，采用巖石平磨機對試件的2個端面進行打磨，打磨后的試件直徑為46 mm，厚度為25.2 mm，端面平整度要求小于0.05 mm。打磨后的試件如圖1所示。

圖1 沖擊壓縮試件Fig.1 Impact compression specimens

1.2 試驗設備及原理

本次試驗采用中國科學技術大學沖擊動力學實驗室研制的Φ50 mm直錐變截面SHPB裝置，加載裝置由子彈系統、入射桿、透射桿及阻尼裝置四部分組成。壓桿全部采用鋼質材料，密度為7 850 kg/m3，波速為5 172 m/s，彈性模量為210 GPa。

采用CS-1D型寬頻帶動態應變儀和TST3406型動態測試儀對波形數據進行采集，采集頻率為 2 MHz。電阻應變片柵長為3 mm，阻值為120 Ω，靈敏度為2.10。

在實際試驗中，由于受到應變片與壓桿貼合緊密性以及試驗過程中的震動等外界因素的影響，應變片靈敏度系數實際值與出廠值之間會存在誤差，需要通過空打來進行校正，壓桿各位置應變片靈敏度系數實際值如表3所示。

表3 應變片實際靈敏度系數表Tab.3 Actual sensitivity coefficient of strain gauge

桿件尺寸及應變片布置如圖2所示。

基于SHPB試驗的2個假設[12-13]，通過彈性波理論及二波法[14]，可推導出試件的平均應力、平均應變及應變率的計算式分別為

(1)

(2)

(3)

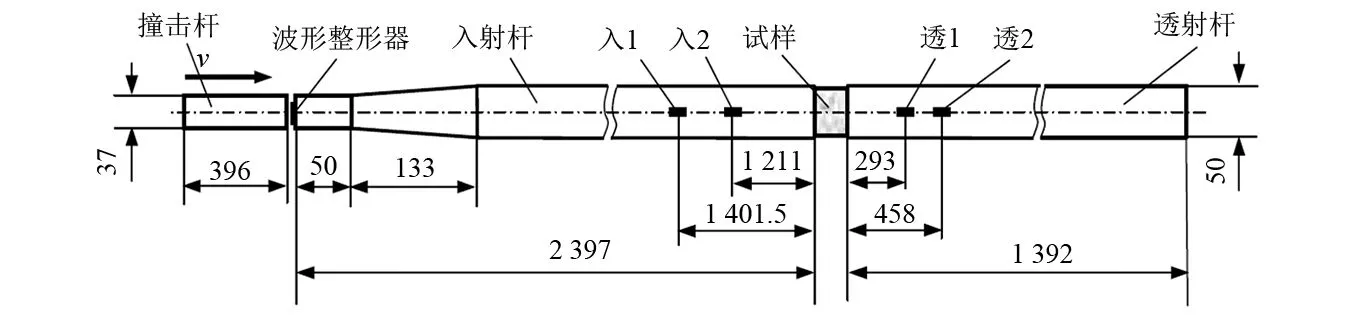
圖2 分離式SHPB試驗裝置(mm)Fig.2 Split SHPB device (mm)

1.3 工況設置

本次試驗預備68個試件，每種纖維摻量有2個備用試件，所有試件按照C1～C68的順序編組。5種不同纖維摻量的試件在S1～S4 4個應變率范圍下，分別進行3次沖試驗，共需進行60次試驗。在實際試驗中，試驗的應變率無法準確預知，只能根據以往試驗經驗及預試驗初步估算子彈在不同氣壓下的撞擊速度以及試件所處的實際應變率范圍。試件編組及應變率范圍設置如表4所示。

表4 試件編組及應變率設置Tab.4 Test piece assembly and strain rate setting

2 試驗結果處理及分析

2.1 數據處理方法

應變片記錄的是電壓信號，要求得入射桿和透射桿中實際的應力波時程信號，需要進行數據轉換，根據惠斯通對臂橋路的原理，得到電壓信號與應變的關系為

(4)

式中：σ(t)為應變片位置處壓桿中的應力；ε為應變片位置處壓桿中的應變；E為壓桿的彈性模量；ΔU(t)為應變片處的電壓信號；K1為串聯應變片數，取值為2；K2為應變片實際靈敏度系數；U0為每1 000 μ應變對應的電壓，動態壓縮時取值為2 V。

通過式(4)計算得到的試件C2在S1應變率范圍下的典型應力時程曲線，如圖3所示。

圖3 在S1應變率范圍下典型波形時程曲線Fig.3 Typical wave-type time history curve in the strain rate range of S1

2.2 應力應變曲線分析

不同纖維摻量試件在S1～S4應變率范圍下的應力應變曲線，如圖4(a)～圖4(d)所示。由圖4可以直觀看出，各個應力應變曲線大致可以分為3個階段：線性上升階段、非線性上升階段以及卸載階段。

由圖4(a)可以明顯看到，隨著纖維摻量的增加曲線直線上升階段延長，曲線非線性上升階段的峰值強度和峰值應變都增加，曲線的卸載階段差異明顯。纖維摻量為0，0.50%和1.25%的試件卸載段曲線相似，這是由于試件在峰值應力后試件表現出典型的脆性破壞，無法繼續提供承載力，導致應力隨著應變的增加驟降；與以上截然不同的是，纖維摻量為 2.00%和 2.30%的試件卸載階段的曲線與線性上升階段幾乎平行，這說明試件并沒有完全進入塑性破壞階段，卸載后彈性變形恢復。

在圖4(b)中，纖維摻量為2.00%和2.30%的試件的線性上升階段和非線性上升階段曲線趨勢與圖4(a)相同，卸載階段變化較大。原因是隨著應變率的提高，纖維摻量為2.00%和2.30%的試件破壞模式發生變化，卸載階段的可恢復變形消失，脆性破壞特征明顯。

在圖4(c)中，各纖維摻量試件的應力應變曲線變化趨勢與圖4(b)相同，不再贅述。

圖4(d)與其他組數據有著明顯不同，所有試件的應力應變曲線幾乎重合，這表明隨著應變率的提高，纖維摻量對峰值強度的影響逐減小。原因是在高應變率下混凝土類材料的動模量會有較大幅度的提高[15-17]，在S1～S3應變率范圍下彈性模量約為25 MPa，在S4應變率范圍下彈性模量約為45 MPa。PVA纖維彈性模量較低，基體材料與纖維之間的彈性模量差距較大，導致纖維的增強作用不明顯。

圖4 在S1～S4應變率范圍下各纖維摻量試件的應力應變曲線Fig.4 Stress strain curve of each fiber mixing test piece from S1 to S4 strain rate

2.3 動態抗壓強度分析

為了定量表達應變率對動態抗壓強度的影響，引用動態強度增長因子(dynamic intensity factor，DIF)表達應變率效應，即動態強度與靜態強度之比。ECC動態抗壓強度的影響因素主要有2個：一是應變率的影響；二是纖維摻量的影響。

各纖維摻量下DIF與應變率的關系，如圖5所示。由圖5中可知，對于相同纖維摻量的試件來說，動態抗壓強度隨著應變率的增加而增加，應變率增強效應顯著，基體材料的應變率增強效應強于ECC的應變率增強效應。

圖5 DIF與應變率的關系Fig.5 The relationship between the DIF and the strain rate

DIF與纖維摻量之間的關系，如圖6所示。由圖6可知，與應變率的增強規律不同，纖維摻量對動態抗壓強度的影響是復雜的。當應變率在36.5 s-1以下時，試件的動態抗壓強度并不是隨著纖維摻量的增加而簡單地逐步遞增，纖維摻量為0.50%和1.25%的試件相較于基體材料的動態抗壓強度提升并不明顯，纖維摻量為2.00%和2.30%的試件動態抗壓強度有較大的提升，分別提高了10.4%和13.8%。在高應變率范圍下(≥57.8 s-1)，纖維摻量為0.50%和1.25%的試件動態抗壓強度相較于基體材料變化不明顯，纖維摻量為2.00%和2.30%的試件動態抗壓強度有小幅提升,但增幅降低，具體表現為：在S3應變率范圍下，纖維摻量為0.50%和1.25%的試件動態抗壓強度相較于基體材料分別小幅減弱0.8%和3.0%，纖維摻量為2.00%和2.30%的試件動態抗壓強度分別小幅提升2.0%和0.3%；在S4應變率范圍下，纖維摻量為0.50%，1.25%，2.00%及2.30%的試件動態抗壓強度相較于基體材料分別小幅提升3.0%，0.7%，0.2%和2.0%。綜合以上數據可以看出，纖維摻量為0.50%，1.25%的ECC與基體材料在不同應變率下的變化規律相似，表現出明顯的應變率增強效應；纖維摻量為2.00%和2.30%的ECC在較低應變率時，ECC動態抗壓強度增幅較大，在較高應變率時增幅有所減弱。

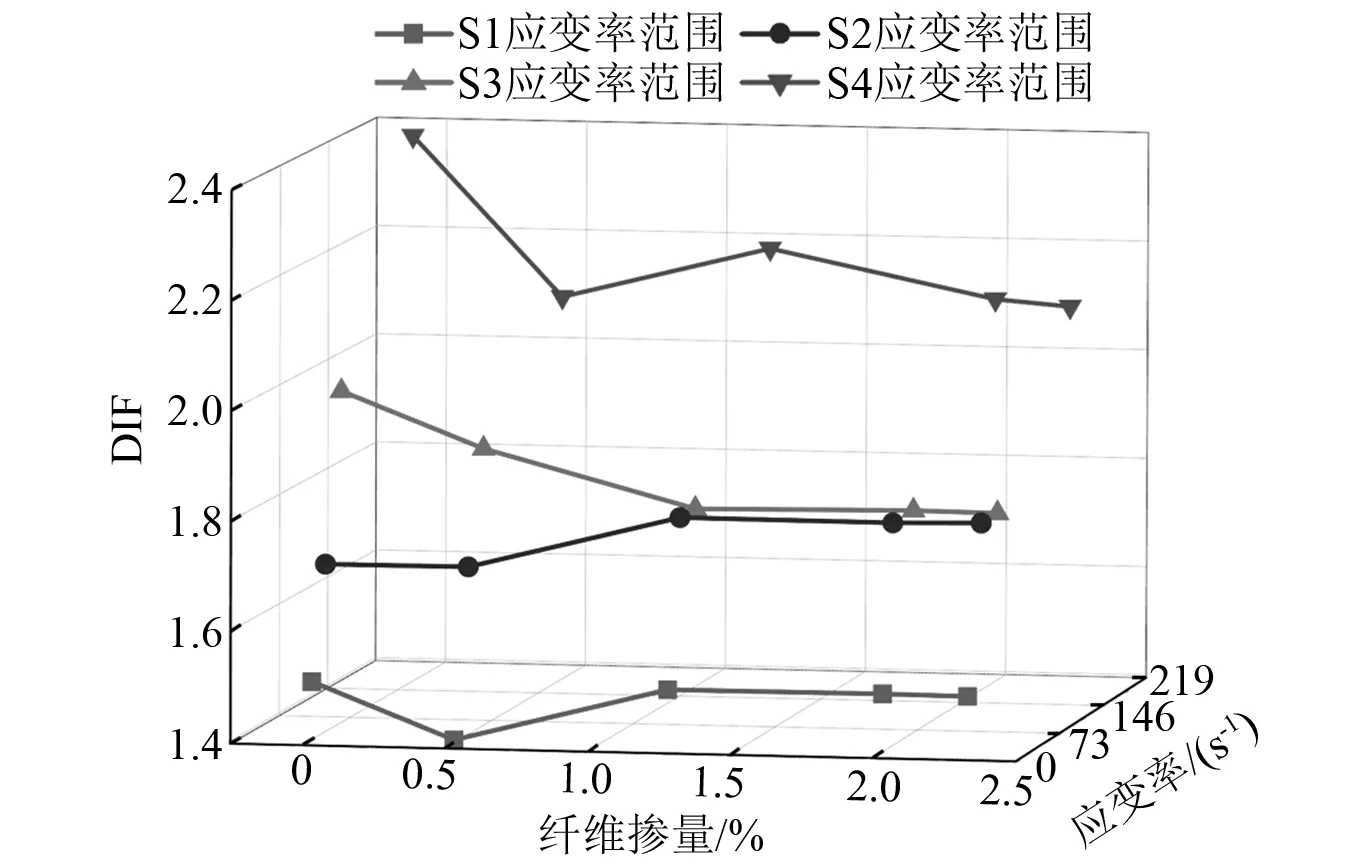
圖6 DIF與纖維摻量的關系Fig.6 The relationship between the DIF and fiber incorporation

寧建國等[18]研究發現，DIF的取值與應變率的對數有一一對應的關系，并得出了

(5)

通過線性回歸擬合得到常數C和D，如表5所示。

表5 C和D擬合值Tab.5 C and D fit values

2.4 動態峰值應變分析

各纖維摻量下峰值應變與應變率的關系曲線，如圖7所示。由圖7中可知，各個曲線的峰值應變具有應變率增強效應，在低應變率時，曲線的斜率較大，纖維摻量對峰值應變的增強作用較為明顯，隨著應變率逐漸提高，曲線斜率趨緩，纖維對峰值應變的影響減弱。

圖7 應變與應變率的關系Fig.7 Relationship between strain and strain rate

各應變率下峰值應變與纖維摻量的三維關系圖，如圖8所示。由圖8可知，隨著纖維摻量的增加試件的峰值應變有提高的趨勢，不同應變下曲線趨勢有所不同。在 S1應變率范圍下，峰值應變增幅隨纖維摻量的增加而增加，摻有 0.50%，1.25%，2.00%和2.30%的纖維的試件峰值應變分別比基體材料增加了2.7%，0.8%，6.4%和20.0%。但隨著應變率的提高，纖維對峰值應變的增強作用減弱，當應變率范圍提高到S4時，摻有0.50%，1.25%，2.00%和2.30%纖維的試件峰值應變增幅分別減少至 0.9%，0.7%，0.7%和1.7%。原因是在應變率較低時，纖維與基體材料之間橋接應力較大，纖維被拉長并與基體之間出現滑移，形成多條裂縫，ECC的峰值應變增幅較基體有明顯的提升；在應變率較高時，纖維與基體之間的橋接應力遠小于斷裂應力，此時纖維表面附著的基體材料瞬間被剝離，纖維與基體之間滑移大幅減弱，導致纖維對峰值應變的影響不明顯。

圖8 應變與纖維摻量的關系Fig.8 Relationship between strainand fiber incorporation

2.5 應變率與纖維摻量對ECC能量耗散的影響

能量耗散是衡量混凝土類材料抗沖擊能力重要的指標之一。在沖擊壓縮荷載下，結構能量的耗散主要分為4個部分：一是結構碎片的動能；二是結構的變形能；三是結構表面裂紋擴展所消耗的表面能；四是小部分的內能、聲能等。文獻[19]表明，試件破碎及表面裂紋擴展所消耗的能量占試件耗散能的95%以上，其次是碎片的動能。

文獻[20-22]給出了SHPB試驗中試件的入射能、反射能、透射能以及耗散能的計算方法

(6)

(7)

(8)

WeD=WeI-WeR-WeT

(9)

式中：WeI為入射能；WeR為反射能；WeT為透射能；WeD為耗散能。

運用式(6)～式(9)得到C44試件的典型能量時程曲線，如圖9所示，其他試件的能量時程曲線可用相同的方法得到。

圖9 纖維摻量為2.00%的試件在S2應變率范圍下的能量時程曲線Fig.9 Energy time curve of fiber incorporation is 2.00% at S2 strain rate level

試驗發現，耗散能的大小與纖維摻量、應變率有關。為了對比纖維摻量及應變率對試件耗能情況的影響，定義了能耗比η，它表示ECC所耗散的能量占受到的實際沖擊能量(入射能-反射能)的比值，表達式為

(10)

通過式(10)計算得到的各纖維摻量的試件在S1～S4應變率范圍下的能耗比，如表6所示。

表6 在S1～S4應變率范圍下不同纖維摻量試件的能耗比Tab.6 Energy consumption ratio of different fiber content specimens in the range of S1-S4 strain rate 單位：%

各纖維摻量下能耗比與各應變率范圍的三維關系圖，如圖10所示。從圖10中可以看出，在S1～S4應變率范圍下，各纖維摻量的試件能耗比隨著應變率的增大而增大，不同纖維摻量的試件的規律有所不同：纖維摻量為2.00%和2.30%的試件能耗比曲線趨勢相近，最終趨于某一值附近；相較于纖維摻量為2.00%和2.50%的試件，纖維摻量為0和0.50%的試件在應變率小于S2時能耗比較高。原因是低纖維摻量的試件在S1和S2應變率范圍下破壞形態均為破碎狀態，透射能較小；較高纖維摻量的試件在上述應變率范圍下表現出較高的強度，塑性變形量較小，碎片較少，入射能量大部分以反射能和透射能的形式表現出來，因此能耗比較低。

圖10 能耗比與應變率的關系Fig.10 The relationship between energy consumption ratio and strain rate

各應變率范圍下能耗比與纖維摻量的三維關系，如圖11所示。由圖11可以看出：在S1應變率范圍下，試件的能耗比隨著纖維摻量的增加明顯提升；在S2～S3應變率范圍下，各纖維摻量試件的能耗比較為接近且均在90%以上。

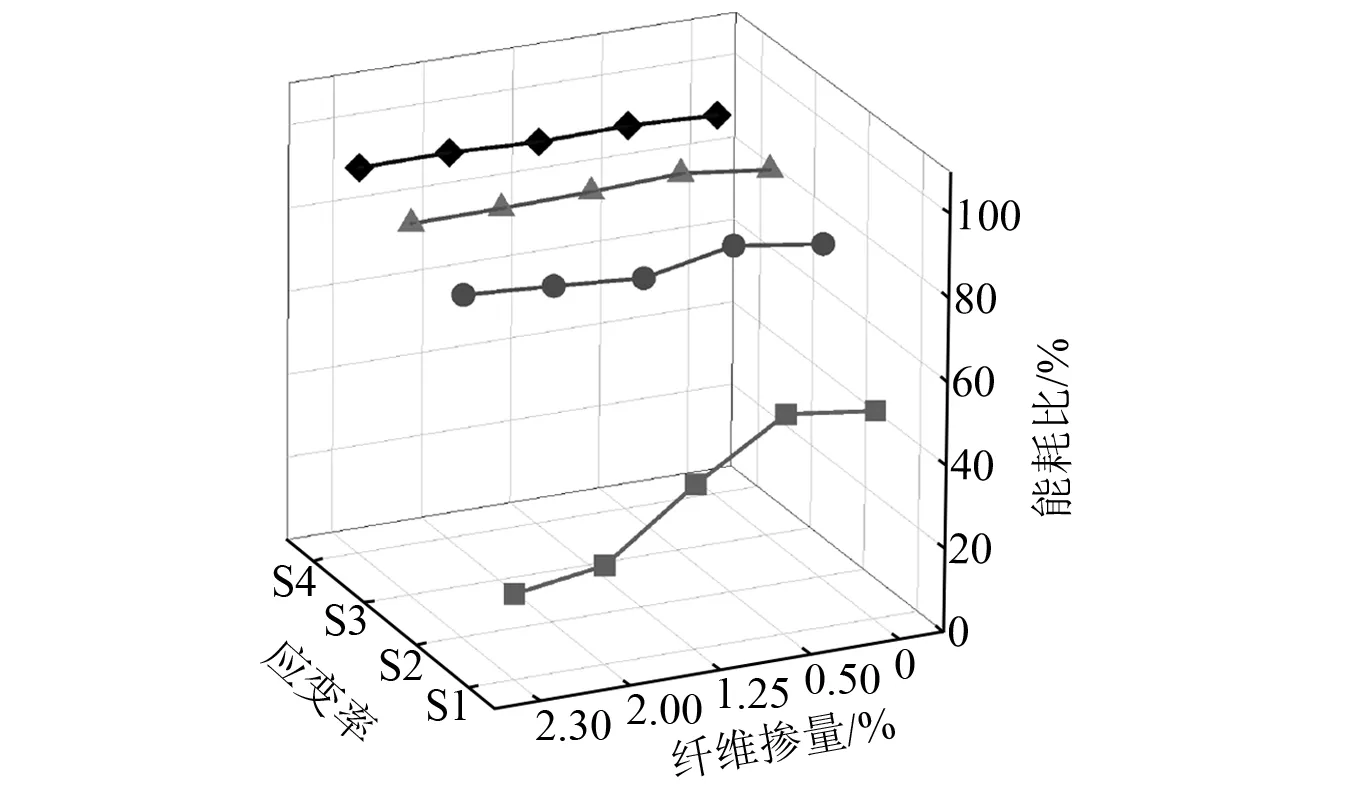
圖11 能耗比與纖維摻量的關系Fig.11 The relationship between energy consumption ratio and fiber mixing amount

2.6 破壞形態與能量耗散的關系

在S1～S4應變率范圍下，不同纖維摻量試件的典型破壞形態，如圖12(a)～圖12(d)所示。由圖12可以看出，破壞程度與應變率、纖維摻量2個因素直接相關。

圖12 在S1～S4應變范圍下各纖維摻量試件的破壞形態Fig.12 Failure morphology of each fiber mixing testin the S1-S4 strain range

為了準確描述試件的破壞程度，以試件碎片平均直徑D作為衡量指標，通過篩分析法[23]定義了D的計算方法

(11)

式中：n為篩網數量；rn為第n個篩網的篩孔直徑；mn為第n個篩網的篩出碎片質量；M為試件質量。篩分析試驗結果如表7所示。

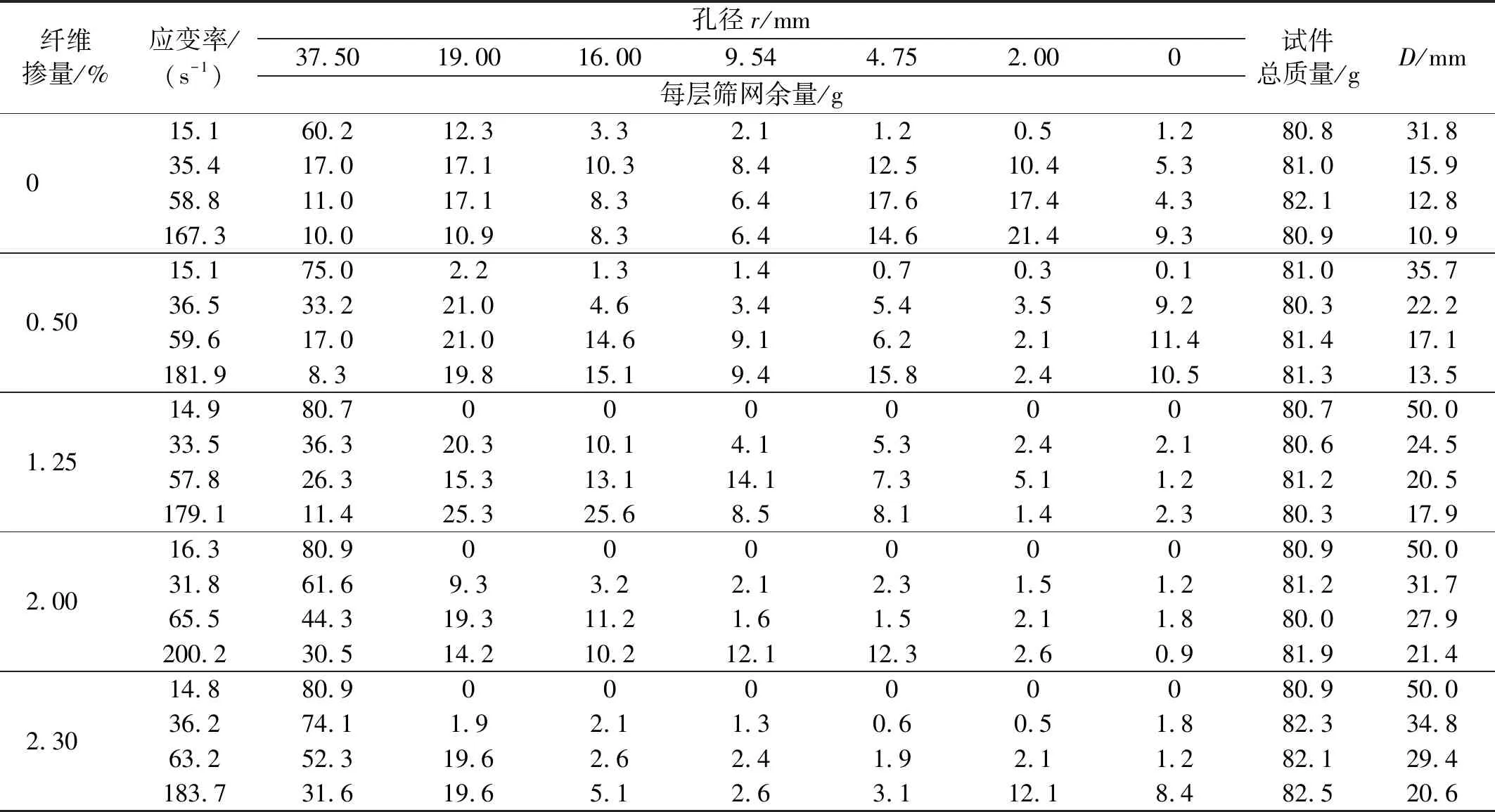
表7 篩分析試驗結果Tab.7 Results of the screening analysis test

為定量分析試件破壞程度與能耗比之間的關系，定義完整度ω，即碎片平均直徑D與試件原始直徑之比，計算式為

(12)

各纖維摻量試件碎片平均直徑D與應變率的關系，如圖13所示。由圖13可以看出，當纖維摻量相同時，隨著應變率的提高，試件碎片直徑越來越小，破壞越來越明顯，表現出水泥基材料在高應變率下具有的脆性特征。

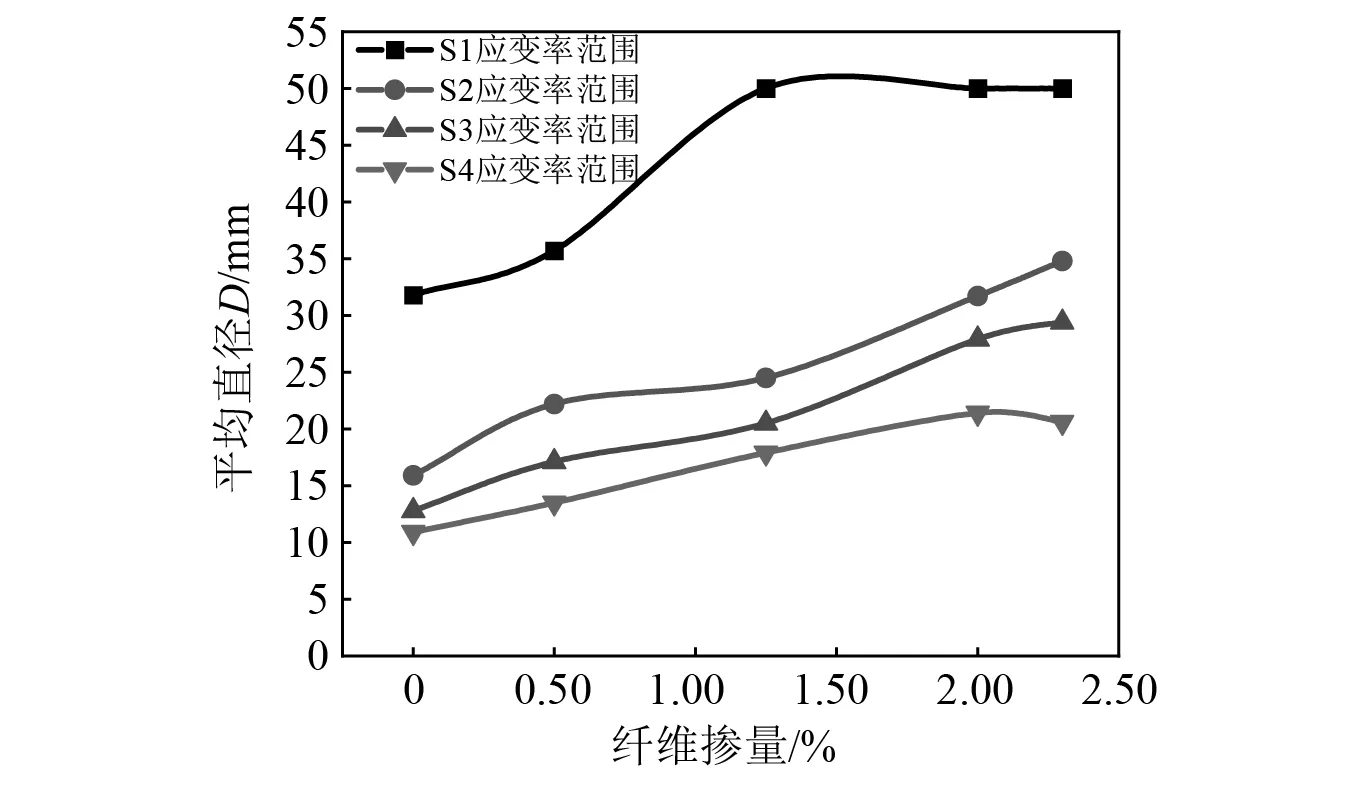
圖13 平均直徑與應變率的關系Fig.13 Relationship between mean diameter and strain rate

試件碎片平均直徑D與纖維摻量之間的關系，如圖14所示。由圖14可以看出，在各應變率范圍下，基體材料的試件碎片平均直徑最小。在S1應變率范圍下，纖維摻量為0.50%，1.25%，2.00%和2.30%的試件碎片平均直徑相較于基體材料分別提高了12.0%，57.0%，57.0%，57.0%；在S4應變率范圍下，分別提高了23.0%，64.0%，96.0%，88.0%。在高應變率下，纖維摻量為2.00%和2.30%的試件碎片平均直徑約為基體材料的2倍，這表明當纖維摻量在2.00%左右時，能夠有效削弱沖擊荷載對結構的破壞作用。

圖14 平均直徑與纖維摻量的關系Fig.14 Relationship between mean diameter and fiber admixture

不同纖維摻量下的能耗比η和完整度ω的變化曲線，如圖15所示。由圖15可以看出，隨著應變率的提高能耗比η逐漸上升，完整度ω逐漸下降，在能耗比η>90%時，纖維摻量為2.00%，2.30%的試件完整度仍能保持在0.4左右，基體材料試件完整度約為0.1，而纖維摻量為0.50%和1.25%的試件完整度則介于兩者之間。這一結論與圖4中的試驗現象相符，充分地說明ECC能夠有效減少建筑結構在沖擊作用下產生的碎片數量，提高結構完整性和穩定性，避免或減少震塌現象對人員和裝備造成的二次傷害。

圖15 完整度、能耗比與應變率的關系Fig.15 Relationship between energy consumption ratio, completeness and strain rate

3 結 論

本文利用SHPB裝置對ECC試件在不同應變率下的動態壓縮特性及耗能機制進行重點研究。主要結論如下：

(1) 在較低應變率(15 s-1)下，隨著纖維摻量的增加 ECC 的應力應變曲線的峰值強度、應變峰值顯著提高，試件的破壞程度逐漸變小；在較高應變率(200 s-1)下,纖維對應力應變曲線的形態影響變小；與基體材料的主要區別表現在隨著纖維摻量的增加軟化階段的曲線斜率變小，殘余強度較基體材料高。

(2) 隨著應變率的提高，ECC的動態抗壓強度和動態峰值應變均具有應變率增強效應。在低應變率下，纖維摻量對DIF的影響不顯著，峰值應變的提升較為顯著；在高應變率下，纖維摻量能顯著降低DIF值，減弱ECC動態抗壓強度應變率強化效應，能夠維持ECC動態抗壓的強度穩定不隨應變率的變化劇烈波動。

(3) 定義了完整度的概念，較合理地量化了ECC的破壞情況。通過分析不同應變率下各纖維摻量的ECC能耗比與完整度之間的關系，得出在應變率較高(200 s-1)下，ECC的能耗比能夠保持在90%以上，纖維摻量為2.00%和2.30%的ECC完整度能夠保持在0.4左右，基體材料的完整度約0.1，ECC能夠有效減弱震塌效應，為ECC在抗爆加固領域的應用提供有益參考。