齒輪傳動系統共存吸引子的不連續分岔1)

金花 呂小紅 張子豪 王昕

(蘭州交通大學機電工程學院,蘭州 730070)

引言

齒輪傳動是機械設備中廣泛使用的動力傳動裝置,其工作性能對整個機器有著重要的影響.因此,齒輪系統動力學的研究引起了許多學者的關注.由于輪齒之間不可避免地存在嚙合側隙,使齒輪傳動系統的動態特性表現出典型的非光滑特征[1-3].隨著振動理論的發展,研究者又在齒輪系統動力學模型中探索齒面摩擦、時變嚙合剛度、時變嚙合側隙和綜合傳遞誤差等各種非線性因素[4-10],使齒輪傳動系統成為一類分段非線性的參數振動系統,具有非常豐富的動力學行為.

多吸引子共存是引起非光滑系統具有豐富動力學行為的一個重要因素.文獻[11-13]提出了計算齒輪系統共存吸引子吸引域的有效方法.新的共存吸引子的出現改變了舊吸引子的全局特性.多吸引子共存時,運動工況的變化以及不可避免的擾動都可能導致齒輪傳動系統在不同運動行為之間跳躍變換,對整個機器產生不良的影響,有時還會引起系統結構的毀壞.因此,非常有必要研究齒輪傳動系統的全局動力學,揭示共存吸引子出現和消失的機制,為齒輪副參數設計與優化、故障預警等提供參考.

在齒輪系統動力學研究領域,單自由度直齒圓柱齒輪傳動系統的動力學模型一直受到國內外學者的廣泛關注,形成了齒輪系統動力學研究的理論體系和分析方法,主要包括多尺度法[14]、增量諧波平衡法[15]、A-算符法[16]和偽不動點追蹤法[17]等.Wei 等[18]改進區間諧波平衡法,解決了齒隙非線性和不確定時變嚙合剛度齒輪系統的動力學問題.陳思雨等[19]研究了不同的嚙合間隙模型對齒輪系統動力學的影響.茍向鋒等[20-21]研究了齒輪系統在兩參數空間的運動形式及其存在的參數區域.Yang 等[22]研究了含非線性間隙單自由度齒輪副的動力學.

在非線性動力系統中,混沌激變是一種常見的不連續分岔行為,包括內部激變和邊界激變.近年來,關于非線性系統的激變研究取得了一些成果[23-25],而對于齒輪傳動系統激變行為的研究很少.

綜合已有的研究論文可發現,單自由度直齒圓柱齒輪傳動系統具有大量的多吸引子共存現象.然而,傳統的單參數分岔分析不能揭示系統的全局動力學.隨著計算機技術的發展,研究者開始運用胞映射的思想研究齒輪系統在參數耦合和狀態空間耦合下的多穩態行為[26-27],但這些研究沒有考慮共存的不穩定吸引子,一些小參數區間存在的穩定吸引子信息沒有被發現,共存吸引子出現和消滅的機制沒有被完全揭示.打靶法是一種求解非線性系統周期解及穩定性的常用方法[28].Chong 等[23]和Jiang 等[29]結合延續算法和直接數值仿真在非光滑系統動力學領域取得了許多有價值的成果.本文應用延拓打靶法和數值仿真兩種方法求解單自由度直齒圓柱齒輪傳動系統共存吸引子的穩定性與分岔,應用胞映射法計算共存吸引子的吸引域,試圖去發現一些新的動力學行為,揭示共存吸引子(包括穩定和不穩定)出現和消滅的機制以及可能發生的不連續分岔.

1 力學模型及Poincaré映射

單自由度直齒圓柱齒輪傳動系統的動力學模型如圖1 所示.圖中,Ii,rbi和 θi(i=1,2) 分別表示主、從動齒輪的轉動慣量、基圓半徑和扭轉角位移,Cg表示嚙合阻尼,k(t) 表 示嚙合剛度,e(t)=eacos(ωt+?e)表示綜合傳遞誤差,2D為嚙合側隙.根據文獻[17],系統的無量綱運動微分方程為

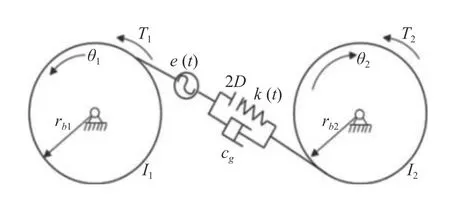
圖1 直齒輪副的力學模型Fig.1 Mechanical model of a spur gear pair

式中,x為無量綱相對位移,ξ為阻尼比,ε為時變嚙合剛度幅值,ω為嚙合頻率,Pm為靜態嚙合力,Pa為時變激勵幅值.g(x)為側隙非線性函數

其中,d為無量綱嚙合側隙的一半.

在不同的系統參數條件下,齒輪系統可能出現三種不同的沖擊狀態: 齒面接觸無碰撞、脫嚙單邊碰撞和齒背接觸雙邊碰撞.令u:=(x,x˙)T∈R2,定義邊界函數:h1(u)=x?d,h2(u)=x+d,則非光滑界面Σ1={u:h1(u)=0}和Σ2={u:h2(u)=0}把系統的狀態空間 劃分為G1={u:h1(u)>0},G2={u:h1(u)<0∩h2(u)>0}和G3={u:h2(u)<0}.方程(1)和(2)寫成如下規范形式

由于系統(3)在各子空間的向量場光滑,因此映射Pi(i=1,2,3)是光滑的同胚映射,其Jacobi 矩陣DPi的求解可轉換為以下矩陣微分方程初值問題

式中,u0i和t0i為軌線在子空間Gi的初值.

2 延拓打靶法

本文應用基于Poincaré映射的打靶法求解系統(3)可能共存的周期吸引子.周期n運動在Poincaré截面的點滿足

式中,T=2π/ω,n=1,2,3. 因此,周期吸引子求解問題可轉化為映射P的不動點問題,即

設分岔參數為v,考察區間v∈[v1,v2],延拓打靶法追蹤共存周期吸引子的方法描述如下.

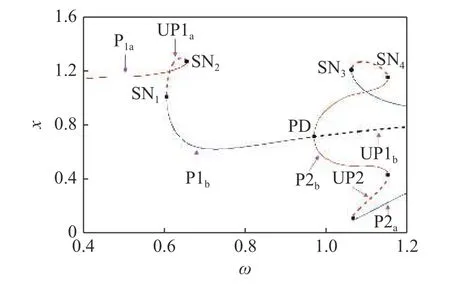
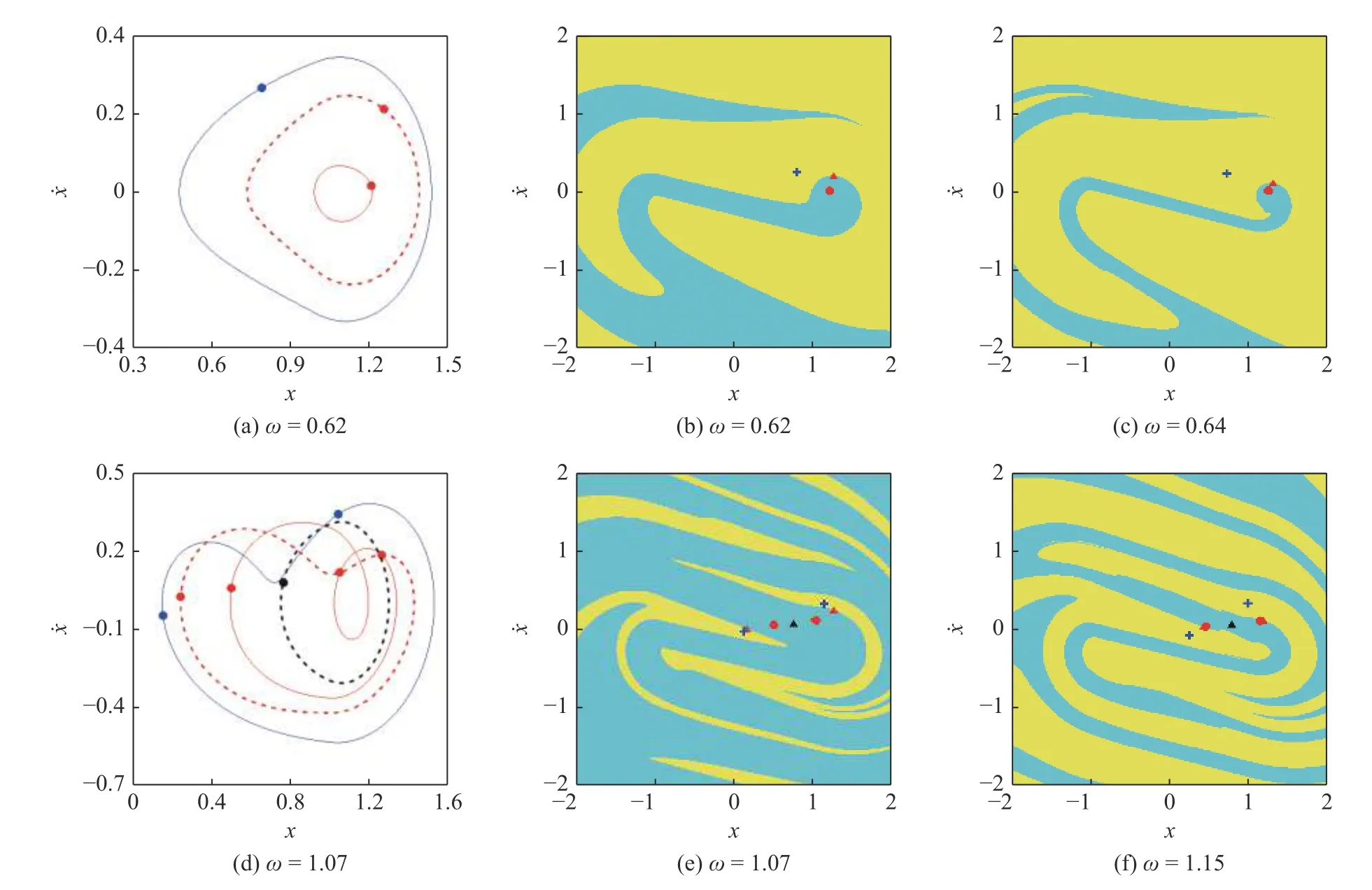
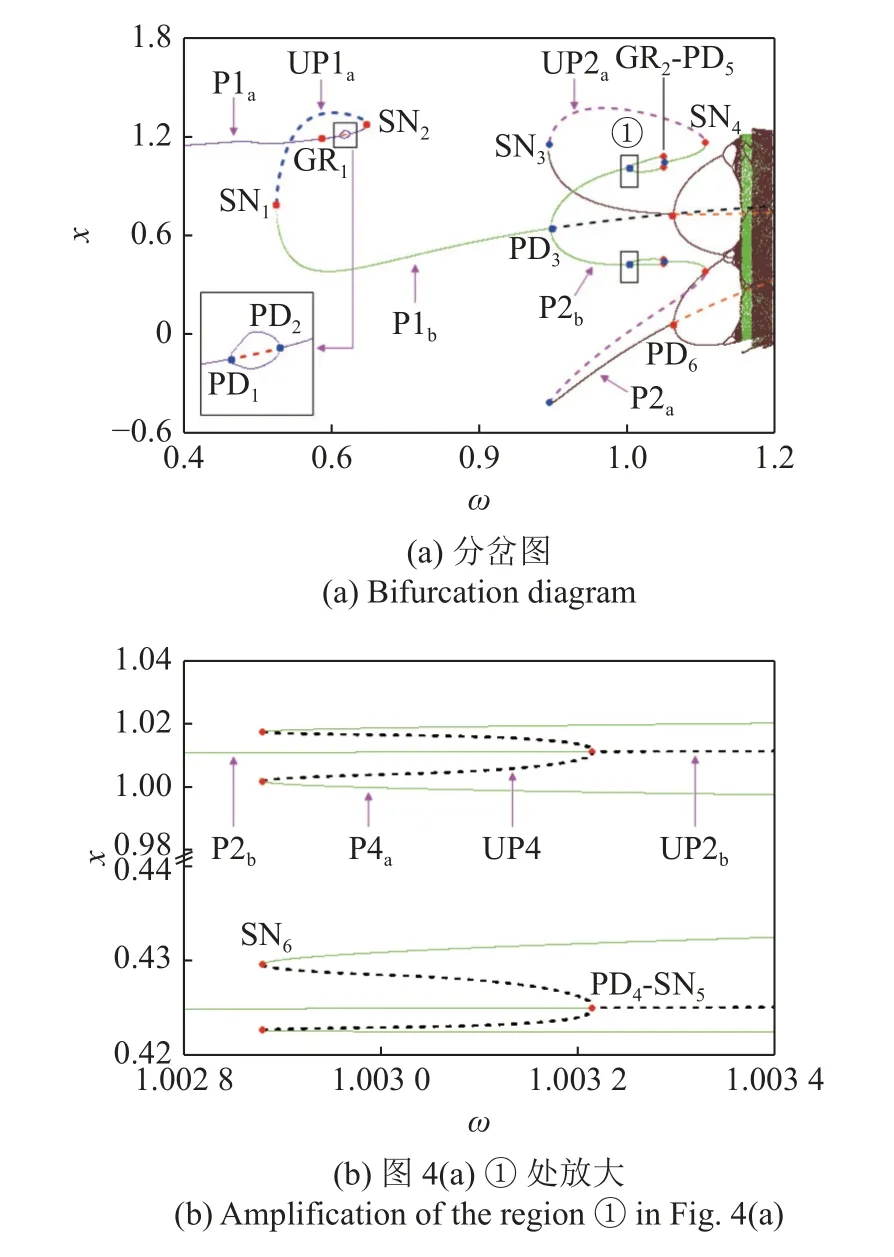
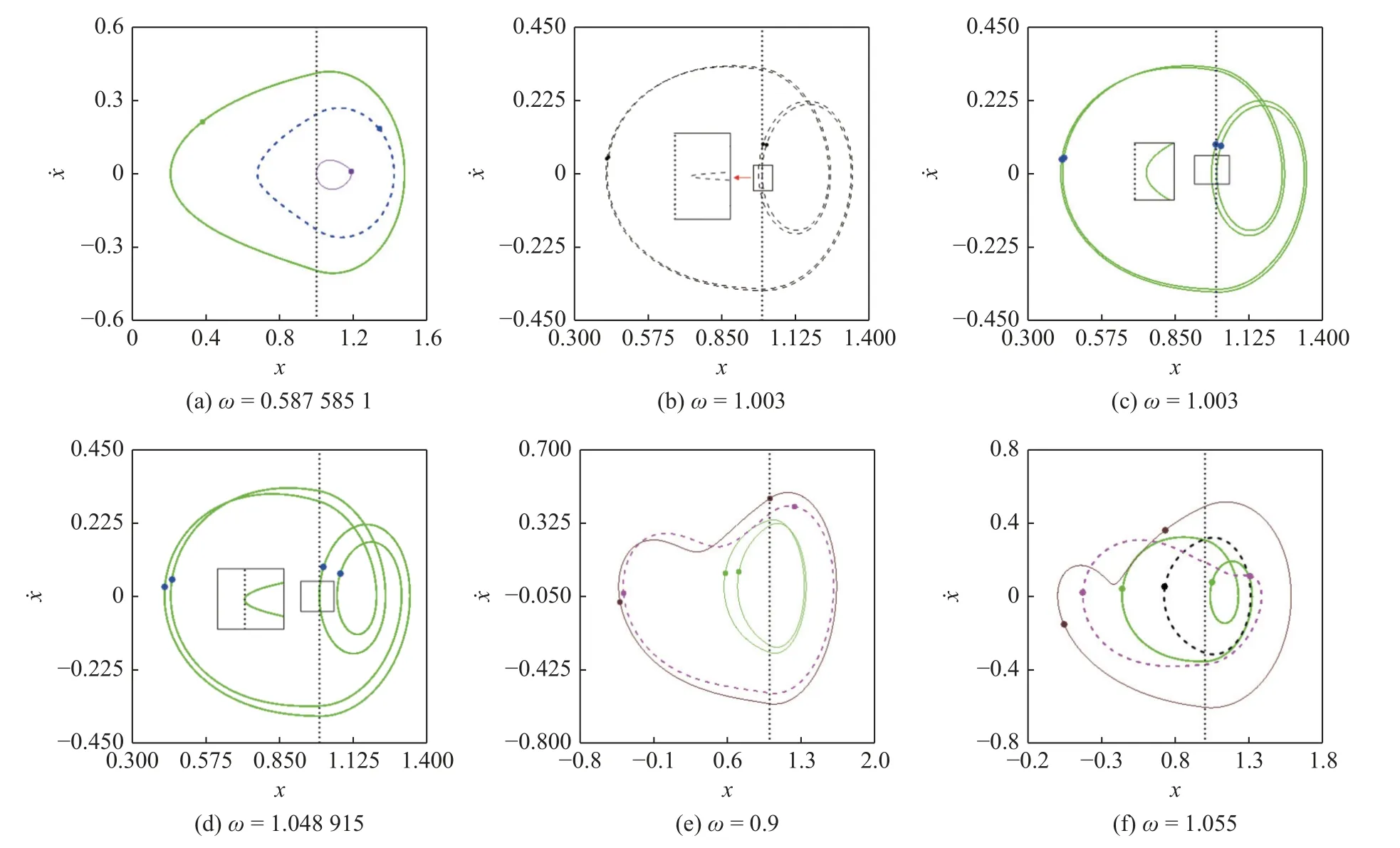
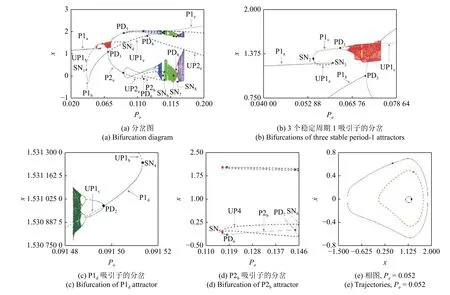
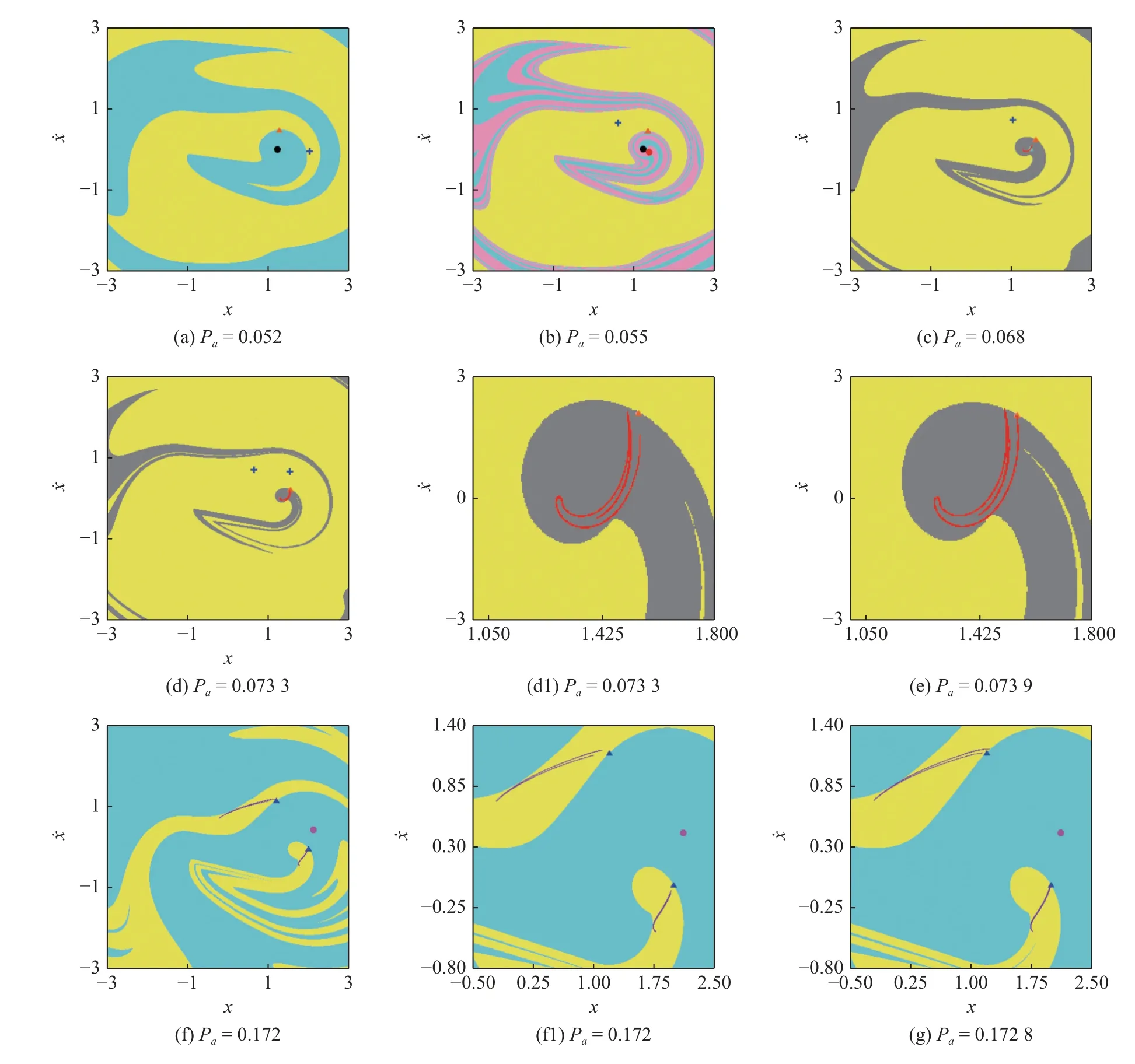
(1) 在Poincaré截面上選擇一個考察區域H=將區域H劃分為m×m=M個小網格,以每個小網格中心點的值作為一個初始不動點u0,應用打靶法計算v=v0(v1

(2) 以 ?v為步長遞增遞減變化參數v,應用延拓打靶法依次追蹤每個共存的周期吸引子在v∈[v1,v2]的穩定性與分岔.為了提高計算效率,在追蹤過程中對初始不動點先用Euler 法進行預估,然后用打靶法迭代校 正.設v=vk時的周 期解為uk,則預估v=vk+1=vk+?v時的初始不動點為

3 全局動力學分析

3.1 共存周期吸引子的分岔

取系統參數(1): ε=0.1,ξ=0.06,Pm=0.1,Pa=0.15ω2和d=1.0,應用延拓打靶法求解系統在ω ∈[0.4,1.2]的響應如圖2 所示.圖中,實線和虛線分別表示穩定和不穩定的周期吸引子;PD 和SNi分別表示倍周期和鞍結分岔點,下標i表示鞍結分岔的發生次序;Pn和UPn分別表示穩定和不穩定的周期n吸引子,用下標a,b,c 區分周期n行為的不同分支.

圖2 延拓打靶法計算的分岔圖Fig.2 Bifurcation diagram calculated by continuation shooting method

由圖2 可見,系統在多處發生鞍結分岔,引起共存周期吸引子的出現或消失.增大ω,在 ω=0.60424242(SN1)時,系統經鞍結分岔出現一對新的周期1 吸引子,分別用P1b和UP1a表示.此后,3 個周期1 吸引子共存.取 ω=0.62,共存周期運動的相圖、Poincaré映射和吸引域見圖3(a)和圖3(b).圖中,相圖與Poincaré映射的顏色與圖2 對應周期吸引子的顏色相同,實線為穩定周期運動的相軌跡,虛線為不穩定周期運動的相軌跡.在吸引域圖中,“●”和“+”表示穩定周期吸引子,“▲”表示不穩定周期吸引子,青色和黃色區域分別為P1a和P1b吸引子的吸引域.可見,共存的三個周期吸引子均表現為單邊碰撞狀態,P1b運動(藍色實線)對應的幅值明顯大于P1a運動(紅色實線)的幅值,UP1a吸引子位于吸引域邊界.繼續增大ω,P1b吸引子的吸引域逐漸擴大壓縮P1a吸引子的吸引域,同時,P1a吸引子與UP1 吸引子相互靠近,見圖3(c).當 ω=0.65406587(SN2)時,系統再次發生鞍結分岔,P1a與UP1a吸引子碰撞并消失.鞍結分岔SN1和SN2在P1a與P1b吸引子的轉遷過程中產生遲滯現象,形成遲滯區.

圖3 相圖、Poincaré映射和吸引域Fig.3 Trajectories,Poincaré maps and basins of attraction

P1b運動在 ω=0.97007516(PD)處通過倍周期分岔失穩.當 ω=1.0614534(SN3)時,系統發生鞍結分岔出現一對新的周期2 吸引子P2a和UP2.此后,3 個周期2 吸引子與1 個不穩定周期1 吸引子共存.共存周期運動的相圖、Poincaré映射和吸引域見圖3(d)～圖3(f).進一步增大ω,P2b與UP2 吸引子在ω=1.1509583(SN4)處碰撞并消失.分岔點SN3和SN4之間形成遲滯區.由圖3 可見,鞍結分岔引起共存吸引子的吸引域較為集中分布,且邊界線光滑,說明系統的終態對初始條件的敏感性較弱,周期吸引子只在局部范圍內不穩定.

3.2 不連續分岔

取ξ=0.01,其余參數保持參數(1)不變,系統在ω ∈[0.4,1.2]的響應如圖4(a)所示.圖中,GRi,PDi和SNi分別表示擦邊、倍周期和鞍結分岔點.采用4 階變步長Runge-Kutta 法的數值仿真只能求解系統的穩定周期解和混沌響應.采用延拓打靶法可追蹤穩定和不穩定的周期解及其演化,并確定分岔值和分岔類型,但前提是給定周期數n.圖4(a)的計算過程描述如下: 首先數值仿真計算ω遞增和遞減變化的分岔圖,得到系統的穩定周期解及混沌響應;然后應用打靶法計算可能存在的共存吸引子及其穩定性;最后應用延拓打靶法追蹤共存的周期1 和周期2 吸引子的分岔.所有計算結果的合成分岔圖如圖4(a)所示.圖中,延拓打靶法和數值仿真兩種方法計算得到的穩定周期吸引子P1a,P1b,P2a和P2b分支完全重合,相互驗證了兩種計算方法的正確性;其余穩定的周期吸引子及混沌由數值仿真方法計算得到,不穩定周期吸引子由延拓打靶法計算得到.圖4(b)為圖4(a)①處的放大.

對比圖2 和圖4 可知,減小ξ使系統的動力學行為更加復雜,主要體現在以下幾個方面: 首先,減小ξ,分岔點SN1～SN4對應的ω值減小,使得在相同的ω區間出現了由P2a吸引子的倍周期序列產生的混沌響應;其次,兩個遲滯區內出現了倍周期分岔,使得共存周期吸引子的類型更加豐富;最后,遲滯區內發生了擦邊及亞臨界倍周期誘導的分岔,進一步豐富了齒輪系統的動力學.

圖4 兩種方法計算的合成分岔圖Fig.4 Composite bifurcation diagram calculated by two methods

由圖4(a)可見,增大ω當 ω=0.5875851(GR1)時,系統發生擦邊分岔引起P1a行為由齒面接觸無碰撞狀態轉遷為嚙合輪齒接觸、脫離、再接觸的單邊碰撞狀態.GR1點處共存周期運動的相圖和Poincaré映射見圖5(a).P1a運動在GR1點的擦邊分岔是連續的,但是緊接著發生的倍周期分岔PD1(ω=0.61180134)使P1a吸引子失穩.GR1點與PD1點之間的距離 ? ω=0.02421624,產生于GR1點的對應單邊碰撞狀態的穩定周期1 運動存在的區間很窄,因此,倍周期分岔PD1是擦邊GR1誘導的分岔,可稱為倍周期型擦邊分岔(GR1-PD1).繼續增大ω,不穩定的周期1 吸引子經倍周期分岔PD2(ω=0.62573255)恢復穩定.文獻[29]研究了碰撞振子擦邊誘導的倍周期分岔和鞍結分岔,但是關于齒輪傳動系統擦邊誘導的分岔研究還未見報道.

圖5 相圖和Poincaré映射Fig.5 Trajectories and Poincaré maps

在分岔點SN3和SN4之間的遲滯區內,系統發生了周期2 吸引子P2b的倍周期分岔.增大ω當 ω=1.00325965(PD4) 時,Floquet 特征乘子為λ1=?1.0,λ2=?0.221 83,由Floquet 理論可知,系統發生倍周期分岔,P2b運動失穩.然后在 ω=1.05091356(PD5) 時,Floquet 特征乘子為 λ1=?0.999 96,λ2=?0.238 27,系統再次發生倍周期分岔,不穩定的周期2 吸引子UP2b恢復為P2b.

在PD4點,系統終態由P2b運動跳躍為P4a運動,因此,分岔PD4為亞臨界倍周期分岔.P2b與P4a吸引子的轉遷細節由圖4(b)描述.應用延拓打靶法詳細計算可知,倍周期分岔PD4是連續的,P2b運動連續地轉遷為周期4 運動P4b.但是,P4b吸引子存在的ω區間非常窄,? ω=0.000 001 3.當 ω=1.00326095(SN5) 時,Floquet 特征乘子為 λ1=1.0,λ2=0.057 71,系統發生鞍結分岔,P4b吸引子失穩發出朝后彎曲的不穩定分支UP4.此后,減小ω當ω=1.00288072(SN6) 時,Floquet特征乘子為λ1=1.000 03,λ2=0.049 45,系統再次發生鞍結分岔使UP4 吸引子變為向ω增大方向延伸的穩定周期4 吸引子P4a.UP4 運動的相圖和Poincaré映射見圖5(b),共存的P4a運動由圖5(c) 描述.增大ω,P4a運動在 ω=1.048915(GR2)處發生擦邊分岔,隨后經倍周期分岔PD5返回P2b運動.P4a擦邊運動的相圖和Poincaré映射見圖5(d).

由于SN5點距離PD4點非常近,因此,鞍結分岔SN5是由倍周期分岔PD4誘導的分岔,分岔PD4可定義為鞍結型亞臨界倍周期分岔(PD4-SN5).分岔SN5的發生引起P2b與P4a吸引子轉遷的跳躍與遲滯,使倍周期分岔PD4呈現亞臨界特性,這個分岔行為與光滑動力系統的亞臨界倍周期分岔明顯不同.目前,關于倍周期分岔誘導的分岔研究還未見報道.

如圖4(a)所示,系統在 ω=0.89451253(SN3)處因鞍結分岔出現P2a和UP2a吸引子,與已有的P1b吸引子共存.在PD3(ω=0.89730321)點,P1b運動變為P2b運動.圖5(e)和5(f)表明,P2a和UP2a運動的幅值大于P2b運動的幅值.

文獻[21,31]應用幅值波動云圖和安全盆的方法研究了系統參數對圖1 所示系統扭轉振幅、沖擊狀態及運行穩定性的影響.由圖2～圖5 可知,隨著嚙合頻率ω的遞增變化,因鞍結分岔出現的穩定周期吸引子的幅值大于已有周期運動的幅值,使得系統在一部分初值條件下的運動可能變得不安全,從而影響齒輪運行的穩定性.或者,齒輪傳動系統因工況變化或擾動從一種周期運動跳躍到另一種周期運動,同時伴有運動幅值的跳躍,這種跳躍直接影響齒輪系統的安全穩定運行,甚至引起系統結構的毀壞.

4 時變激勵幅值的影響

取 ω=0.4,其余參數與參數(1)相同,計算系統隨時變激勵幅值Pa變化的分岔圖如圖6(a)所示.開始于Pa=0.02 的周期1 吸引子用P1a表示.在Pa=0.04034294(SN1)和Pa=0.05442717(SN2)處,兩次鞍結分岔使系統出現2 對新的周期1 吸引子,用P1b和UP1b及P1c和UP1a表示.3 個穩定周期1 吸引子的分岔細節見圖6(b).隨著Pa的增大,P1a與UP1a吸引子在Pa=0.06011385(SN3)處相遇并消失;P1c吸引子經開始于Pa=0.06233423(PD1)處的倍周期序列變為混沌吸引子,然后經邊界激變消失,P1c吸引子的穩態分岔分支終止.

增大Pa追蹤在PD1點失穩的不穩定周期1 吸引子UP1c.當Pa=0.09149646(PD2)時,UP1c吸引子經倍周期分岔恢復穩定,用P1d表示.由圖6(c)可知,P1d吸引子存在的區間非常窄,在Pa=0.09151304(SN4)處與UP1b吸引子相遇并消失.

P1b吸引子在Pa=0.07022021(PD3)時經倍周期分岔產生一個穩定吸引子P2a的分岔分支和一個不穩定吸引子UP1e的分岔分支.首先追蹤UP1e吸引子分支的分岔.當Pa=0.12330612(PD4)時,倍周期分岔使UP1e吸引子變為穩定,然后一直持續到Pa=0.2,用P1e表示.特別強調的是,分岔PD4為P1e吸引子的鞍結型亞臨界倍周期分岔.當參數Pa減小時,P1e吸引子在PD4點發生倍周期分岔產生穩定的周期2 運動(存在的區間太窄 ?Pa=0.0000024,圖中沒有顯示).隨后在Pa=0.12330588 處經鞍結分岔發出朝Pa增大方向延續的不穩定周期2 吸引子UP2e,一直到Pa=0.2.

增大Pa追蹤P2a吸引子分支的分岔.當Pa=0.09102000(PD5)時,P2a吸引子失穩產生一個穩定周期4 吸引子分支和一個不穩定周期2 吸引子UP2a分支.穩定周期4 吸引子經倍周期序列變為混沌吸引子(藍色),然后經邊界激變消失.UP2a吸引子在Pa=0.11809877(PD6)處經倍周期分岔恢復穩定,用P2b表示.P2b吸引子的分岔細節由圖6(d)描述.可見,P2b吸引子由兩個倍周期分岔點PD6和PD7限制.分岔PD6為鞍結型亞臨界倍周期分岔,而分岔PD7為超臨界倍周期分岔.減小Pa,開始于PD6點的穩定周期4 運動在SN5點失穩發出朝Pa增大方向延續的不穩定周期4 吸引子UP4.此后,增大Pa,UP4 吸引子與產生于Pa=0.14453066(PD7)處的穩定周期4 運動在SN6點相遇,系統終態經鞍結分岔變為混沌響應.繼續增大Pa,在Pa=0.15877421(SN7)處,系統經鞍結分岔出現一對新的周期2 吸引子.穩定周期2 吸引子經開始于Pa=0.16210200(PD8)處的倍周期序列通向混沌,而不穩定周期2 吸引子在Pa=0.16448391(SN8)處經鞍結分岔消失.

圖6 隨Pa 變化的分岔圖和相圖Fig.6 Bifurcation diagram of displacement as a function of Pa and trajectories

圖6 顯示系統存在大量的多吸引子共存現象.鞍結分岔是周期吸引子出現或消失的主要原因,混沌邊界激變是周期吸引子的分岔終止的一個重要因素.圖7 計算了共存吸引子的吸引域演化以揭示鞍結分岔和邊界激變的分岔結構.圖7(a) 中,P1a和P1b吸引子分別用“●”和“+”表示,其吸引域分別用青色和黃色表示,UP1b吸引子位于吸引域邊界.共存周期運動的相圖和Poincaré映射見圖6(e).可見,P1a運動表現為齒面接觸無碰撞狀態,UP1b運動表現為單邊碰撞狀態,而P1b運動表現為雙邊碰撞狀態.增大Pa,P1b吸引子的吸引域逐漸擴大,而P1a吸引子的吸引域逐漸縮小.SN2點后,共存的吸引子增加了P1c和UP1a.穩定周期1 吸引子P1c的出現破壞了P1a吸引子的吸引域結構,使得系統在一部分初值下的P1a響應跳躍為P1c響應,見圖7(b).P1c吸引子的吸引域用粉紅色表示.P1a與P1c吸引子的吸引域邊界呈現一定的自相似分形結構.繼續增大Pa,P1b和P1c吸引子的吸引域逐漸擴大,壓縮P1a吸引子的吸引域.P1a與UP1a吸引子在SN3點相遇并消失.P1c吸引子經倍周期序列通向混沌.此后,系統的終態為P1b與混沌吸引子共存.圖7(c)中紅色表示的混沌吸引子很小,其吸引域用灰色表示,共存的UP1b吸引子仍然位于吸引域邊界,而UP1c吸引子位于灰色吸引域內.由圖7(c)～圖7(e) 可見,其中圖7(d1)為圖7(d)的局部放大,進一步增大Pa,混沌吸引子逐漸長大,混沌的吸引域逐漸減小,混沌與UP1b吸引子相互靠近.在PD2點,P1b吸引子分岔為P2a吸引子,系統的終態變為P2a與混沌吸引子共存.當Pa=0.073963 時,混沌吸引子與UP1b吸引子碰撞,系統發生邊界激變導致混沌吸引子及其吸引域突然消失,系統終態只表現為P2a運動.

圖7 吸引域Fig.7 Basins of attraction

圖7(f)、圖7(f1)和圖7(g)描述了系統終態為周期1 運動P1e與混沌共存的吸引域演化.用紫色表示的混沌吸引子由開始于PD8點的倍周期序列產生,吸引域用黃色表示.P1e吸引子的吸引域用青色表示,UP2e吸引子位于吸引域邊界.增大Pa,混沌吸引子與UP2e吸引子相互靠近.當Pa=0.172925 時,混沌吸引子與UP2e吸引子碰撞,同時與吸引域邊界相切,系統發生邊界激變導致混沌吸引子及其吸引域突然消失,系統終態只表現為P1e運動.

5 結論

本文考慮單自由度直齒圓柱齒輪傳動系統,構建由局部映射復合的Poincaré映射,推導了Jacobi 矩陣特征值計算的半解析解.應用數值仿真、延拓打靶法和Floquet 特征乘子求解共存吸引子的穩定性與分岔,應用胞映射法計算分析了共存吸引子的吸引域演化,討論了嚙合頻率、阻尼比和時變激勵幅值對系統動力學的影響,揭示了倍周期型擦邊分岔、亞臨界倍周期分岔誘導的鞍結分岔和邊界激變等不連續分岔行為.

倍周期分岔誘導的鞍結分岔引起相鄰周期吸引子相互轉遷的跳躍與遲滯,使倍周期分岔呈現亞臨界特性,這個分岔行為與光滑動力系統的亞臨界倍周期分岔明顯不同.鞍結型亞臨界倍周期分岔的發現和定義將進一步豐富非光滑系統的動力學.

鞍結分岔是共存周期吸引子出現或消失的主要原因,邊界激變是周期吸引子的分岔終止的一個重要因素.擦邊分岔和倍周期分岔對吸引域結構沒有影響,不影響系統的全局特性,而鞍結分岔由于產生了新的穩定周期吸引子,改變了舊吸引子的吸引域結構.鞍結分岔產生的不穩定周期吸引子位于穩態吸引子的吸引域邊界.當分岔參數變化時,混沌吸引子與位于吸引域邊界的不穩定周期行為發生碰撞使系統發生邊界激變,混沌吸引子及其吸引域突然消失,對應周期吸引子的分岔終止.

為了保證齒輪傳動系統的運行安全,其運轉過程中的振動幅值必須控制在合理的范圍內.當鞍結分岔引起新的周期吸引子出現時,其運動的幅值可能遠大于已有周期運動的幅值.此時,擾動會使系統終態及振動幅值發生跳躍,影響齒輪系統的安全穩定運行,甚至引起系統結構的毀壞.

單自由度直齒輪傳動系統表現出非常豐富的動力學行為,本文以新的視角發現了許多復雜的新現象,對進一步揭示齒輪傳動系統的振動特性具有重要的意義.